武警部隊搶險救援任務
張亞楠 王浩鑫


摘要:武警部隊肩負著維護國家安全、保障人民安居樂業等神圣使命。本文主要研究突發自然災害時,救援物資的運送問題。
針對問題一,分別計算兩個駐扎點途經補給站到兩個受災區的最短時間,再分配救援對象。計算最短時間時,采用0、1分配,以最短時間為目標函數,一個車隊只救援一個受災區為約束函數,建立優化模型,求解救援方案,最優救援路徑見表3。
針對問題二,分別計算兩個駐扎點途經補給站到10個受災區的最短時間,再采用0、1分配,以最短時間為目標函數,一個車隊只救援一個受災區為約束函數,建立優化模型,得到最優救援路徑見表6。
關鍵詞:救援方案 0、1分配 優化模型
一、問題重述
某地區發生地震災害,需要武警部隊裝載救援物資、迅速完成救援搶險任務,受災地區的道路圖如附件1,其中,紅線是主干道路,為雙車道,行駛速度為70公里/小時;藍線為單車道,速度為45公里/小時,且機動車只能在道路節點會車。D1、D2兩區域分別駐扎兩個中隊,Z01-Z02為6個物資補給區域,F01-F60為60個村莊。各物資補給區域每次只能容納1個機動中隊,每個中隊物資裝卸需要10分鐘。
解決以下問題:
(1)若F02、F55為地震重災區,設計從D1、D2出發到F02、F55的最優路徑以順利完成任務。
(2)若F02、F58、F14、F16、F41、F46、F49、F55、F57、F60為地震重災區,從D1、D2向受災區輸送救援物資,D1、D2兩區域的中隊分別統一行動,然后返回駐扎點繼續下一個輸送任務。設計救援路徑,使用時最少。
二、問題分析
針對問題一
我們假設車隊出發時未裝載物資,則需要先去物資補給區域進行補給,然后再去受災區。由于不確定哪個中隊救援哪個受災區,所以我們先分別求出D1、D2經過6個補給站到F02、F55的最短時間,再進行比較得出救援組合方式。
求時間時,采用0、1分配,以最短時間為目標函數,一個車隊只救援一個受災區為約束函數,建立優化模型,求解救援方案,從而得出最短救援時間。
針對問題二
同樣假設車隊出發時未裝載物資,則需要先去物資補給區域進行補給,然后再去受災區,返回駐扎點再繼續下一個救援任務。時間為車隊往返駐扎地的時間,以時間最短為目標函數,一個車隊只救援一個受災區為約束函數,建立優化模型。
三、模型假設
1.假設車隊在道路上行駛時沒有其他時間損耗;
2.假設問題一、二車隊出發時未裝載物資。
四、符號說明
五、模型建立和求解
5.1問題一模型建立和求解
5.1.1數據處理
為了方便編寫MATLAB程序,將附件中的要素編號按順序重新編號為1,2,3……130,并且將題中所給圖形中相連的線段的起點和終點依次找出,保存在附件2。結合每個節點的坐標,利用MATLAB里的graphshortestpath算法[1],編寫程序(見附錄)將每條道路的路程求解出來,進而得到經過每條道路所花費的時間。
5.1.2模型建立
采用0、1分配,設第i個重災區由j個駐扎地救援為1,否則為0則有:
設第一個重災區是F16,第二個重災區是F55,第一個駐扎地是D1,第二個駐扎地是D2。要求武警部隊一個駐扎地出發后,先經過補給點補給物資,再運往重災區,且一個駐扎地只救援一個重災區,一個重災區只被一個駐扎地救援,得到約束條件,。兩個駐扎地的武警部隊是同時行動,要求花費時間長的路線所用時間盡可能的少,則有,綜上得到優化模型:
5.1.3模型求解
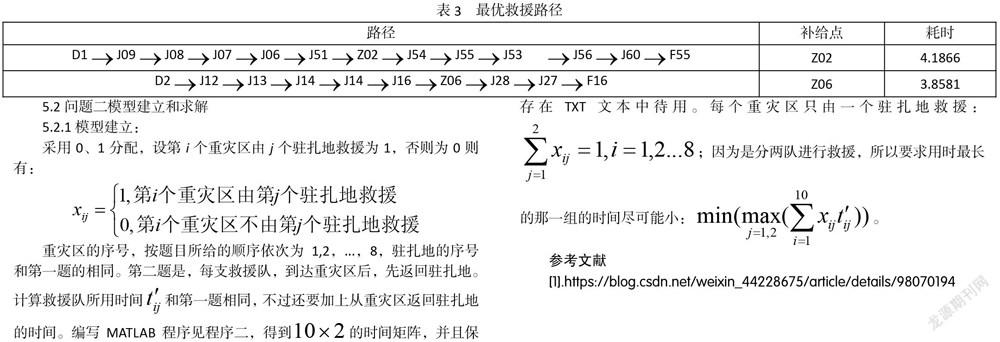
將計算得到的每條道路的時間矩陣,進行對角化和稀疏化處理,然后調用MATLAB圖論工具箱中的graphshortestpath函數[1],任意給定起點和終點,就可以得到兩點所花費的時間和經過的節點。計算駐扎地到重災區的時間時,中間可以經過的物資補給點一共有6個,依次計算經過每個補給點的總時間,保留時間最小的那一條路徑,記錄補給點的序號,編寫MATLAB程序見附錄程序一,得到時間表見表1,補給站經過表見表2:
本題數據較少,可以不用LINGO進行求解,觀察即可得到D1的救援隊在Z02進行補給之后前往F55,D2的救援隊在Z06進行補給之后前往F16,具體路徑如表3。
5.2問題二模型建立和求解
5.2.1模型建立:
采用0、1分配,設第i個重災區由j個駐扎地救援為1,否則為0則有:
參考文獻
[1].https://blog.csdn.net/weixin_44228675/article/details/98070194
西安理工大學 710048

