多種混合智能算法在城市水環境綜合整治中應用的研究

2

(1.中山市環境保護技術中心，廣東 中山 528400;2.暨南大學水生生物研究中心，廣東 廣州 510632)

目前，人們對環境保護愈發重視，針對城市水環境污染的綜合整治是我國環境保護領域的一個重要工作，同時也是城市環境治理中的一個重要環節[1]。2015年，由國務院印發的《水污染防治行動計劃》中提出：“直轄市、省會城市、計劃單列市建成區要于2017年底前基本消除黑臭水體。”同時提出到2020年，長江、黃河、珠江、松花江、淮河、海河、遼河等七大重點流域水質優良(達到或優于Ⅲ類)比例需要總體達到70%以上。

城市中河涌水體是城市水污染物排放的主要受體，接納著來自生活污水、工業廢水等多種類型的水污染物，城市河涌是整個城市生態空間的一項重要構成要素，同時也是城市水循環系統的關鍵部分。引起城市河涌水體污染的因素很多，根據污染主要來源可分為工業企業污染源、居民生活污染源、農業面源污染源及初期雨水污染源等[2]。通對過污染源的現狀評價工作，可以更好地掌握工程區域內的污染物來源、污染總量、污染類型。針對污染源來設定工程措施，更有針對性、更加高效、更加切實可靠。在對城市污染源進行現狀評價的過程中，由于污染源數量巨大、來源復雜，因此對城市河涌水體的研究需要投入大量的人力和物力。

近年來，智能算法在預測與評估等領域，由于其無需準確的數學模型和快速推理機制，且不同智能算法之間匹配時具有良好的兼容性和相互彌補性，應用日益廣泛[3]。在水污染治理和研究過程中，智能算法的出現可以很好地應對水污染治理研究中存在的約束性、非線性、不確定性和建模困難等問題。目前已在河涌水質預測、水環境質量綜合評價、現場工藝控制等方面有所應用[4-5]。吳志遠等[6]提出的基于分段粒子群算法的梯級水庫多目標優化調度模型，有效解決了水庫調度模型在時間步長較小、計算時段數目較多時尋優效率低下的問題。李祥蓉等[7]將靜電放電算法和投影尋蹤融合模型成功應用于水功能區水質綜合評價。本文以中山市南朗流域共13條河涌水體為研究對象，結合當前熱門的智能算法，建立起基于多種混合智能算法的河涌水質預測模型、以高錳酸鹽指數和溶解氧為目標的河涌水質多目標優化模型。

1 數據與方法

1.1 數據來源和分析

中山市南朗流域共有河流59條，屬于典型的河網型流域，河涌分布密集。主要河道有北部排洪渠、中心二河、泮沙排洪渠、蘭溪河等。北部排洪渠位于南朗鎮北面，攔截北部山區的雨洪水，中心二河東西向貫穿南朗城區，兩河道大致平行，相距約450m。泮沙排洪渠位于鎮區中南部，在合水口附近設有一節制閘，水流主要經泮沙排洪渠出海。蘭溪河在鎮區的南部，獨立出海。

本文以中山市南朗鎮南朗流域河涌為研究對象，數據選取中山市南朗流域內的北部排洪渠、中心二河、泮沙排洪渠、蘭溪河、大溪、麻子涌、南沖渠、貝里坑、白企坑、合水坑、大車南渠、大車北渠、東椏涌13條黑臭河涌污染源現狀調查數據和水質現狀監測數據(調查數據來源于《中山市未達標水體綜合整治工程可行性研究報告(南朗流域)》相關章節數據和中山市生態環境局網站相關統計數據，水質現狀監測在河涌枯水期展開，在4月、10月對13條的河涌進行了檢測，水質現狀分析按照國標中規定的有關方法進行)。南朗鎮南朗流域13條河涌地理分布見圖1。

為盡可能全面地考慮不同污染源對河涌水質的影響，本文選取對河涌水質影響最為明顯的污染源類型：

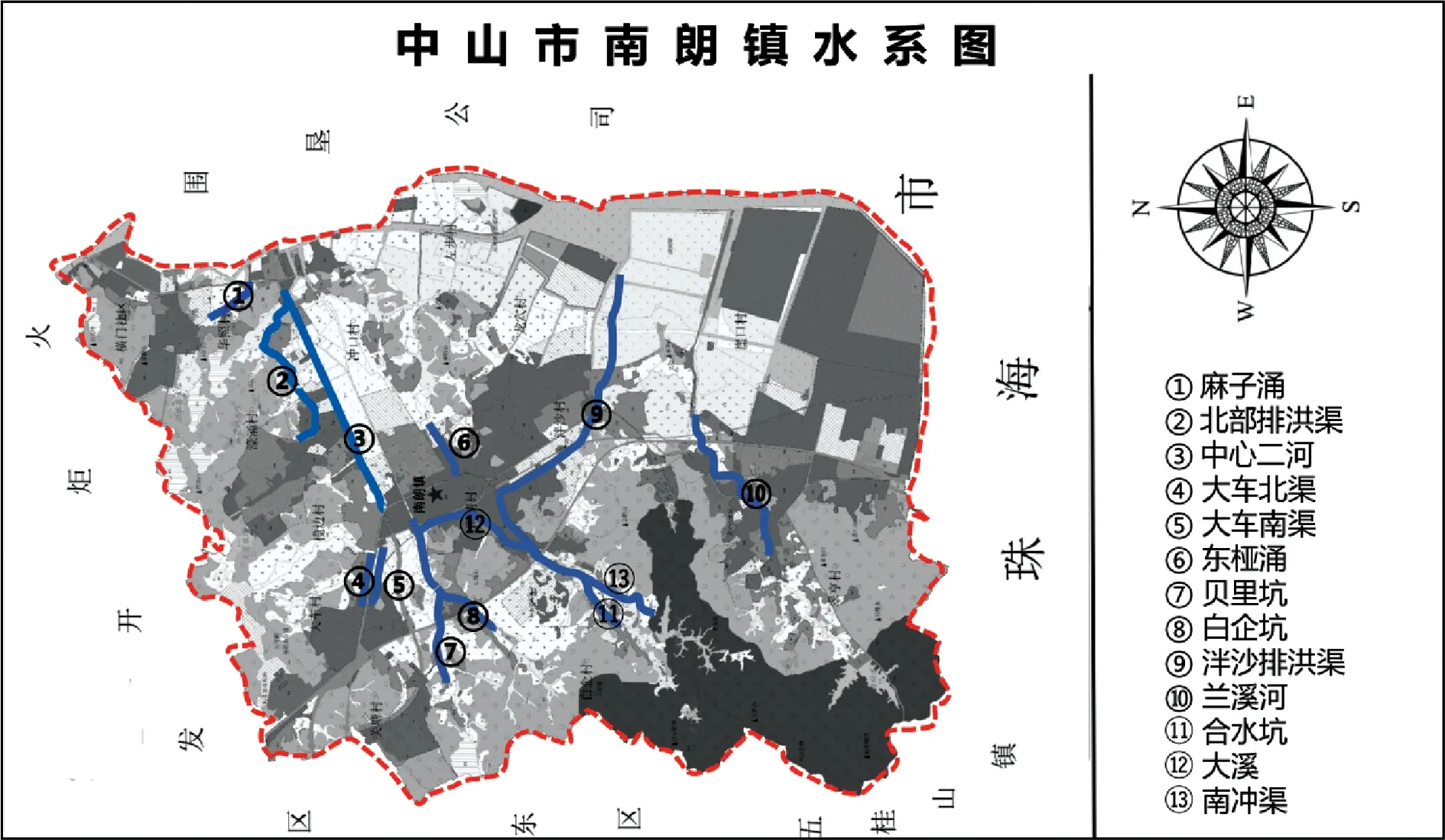
圖1 南朗流域13條河涌分布情況

工業企業污染源、居民生活污染源、農業面源污染源(包括農田和魚塘)和初期雨水污染源(由于流域內的13條河涌多為并行排列狀態，暫不考慮入河支流對主河道的污染入流影響)。調查數據包括統計各條河涌沿岸的居民人口數和河涌沿岸截污管道的敷設情況；針對工業企業污染源，調查各河涌流域的應處理達標的工業廢水污染的入河量；對于農業面源污染，調查出流域內每條河涌排水區域內的農業種植面積及魚塘面積；最后，對流域內各個河涌的水文參數和水質狀況進行匯總。

本文分別選取年生產廢水入河量、居民人口當量、農田面積和魚塘面積、初期降雨總凈流量對工業企業污染源、居民生活污染源、農業面源污染源及初期雨水污染源的影響進行表征。同時，選取河涌集雨面積對河涌自身水環境容量進行表征，水質現狀監測數據以高錳酸鹽指數和溶解氧進行表征。中山市南朗流域13條河涌水質現狀調查數據見表1。

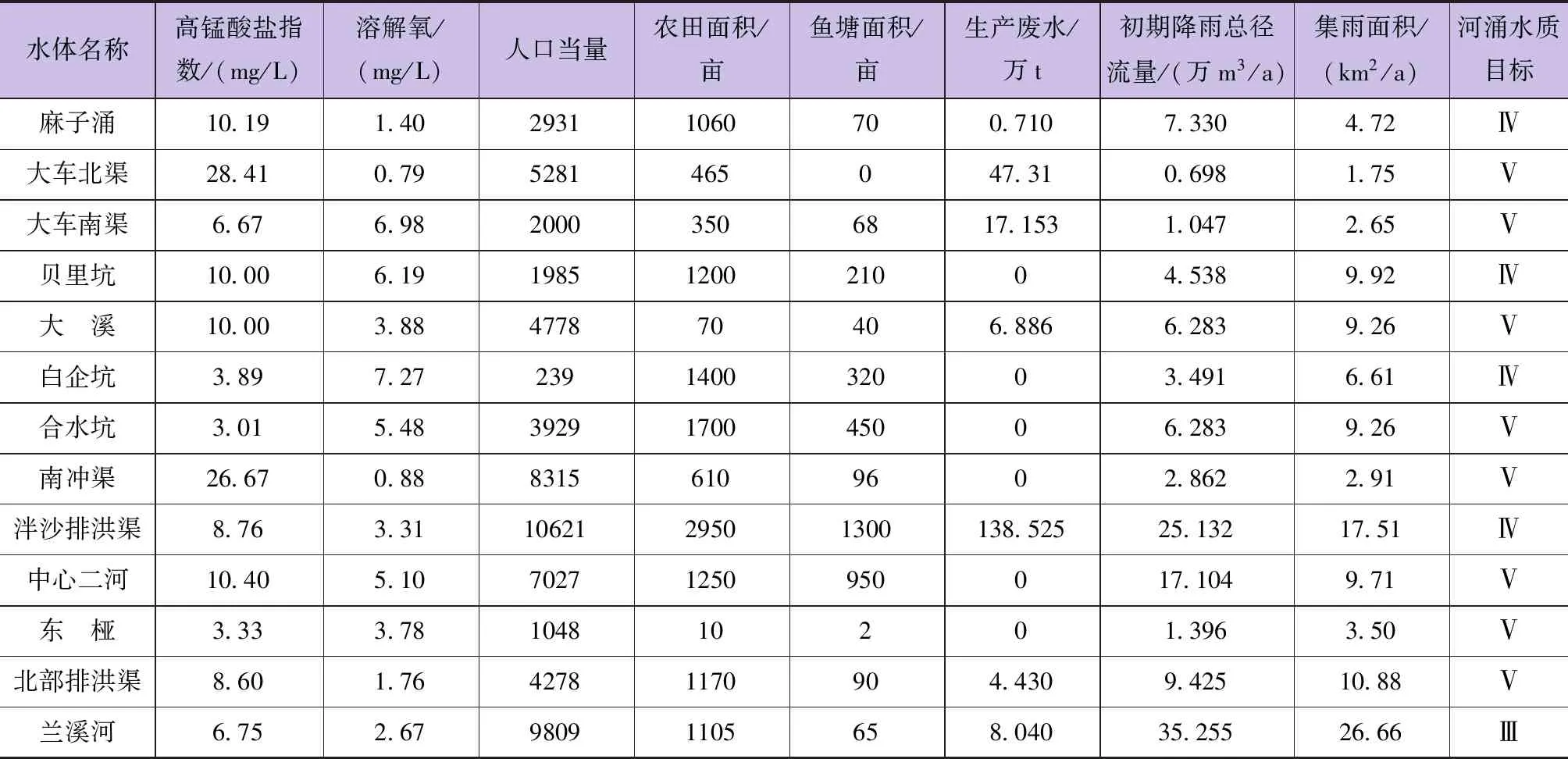
表1 南朗流域13條河涌水質現狀調查數據

1.2 PCA-LSSVM模型的建立

支持向量機(SVM)算法是基于結構風險最小化要求，通過選擇分類核參數類型和其他不同參數，使訓練誤差與測試風險達到最小的智能算法[8]。LSSVM算法則是對SVM的一種變形與拓廣，其在SVM的基礎上，應用訓練誤差的二次平方項代替優化目標中的松弛變量，另一方面，通過將原來的不等式約束改為等式約束，可大大提高計算的運行速度。對比神經網絡的啟發式學習手段，SVM對于數據樣本有較小的依賴性，因此需要更為嚴格的數學論證，其所得的局部最優解可解決神經網絡訓練中易陷入局部極小點的問題。支持向量機是學習算法中一種常用的分類方法，可用于解決實際訓練中存在的樣本數量少、線性不可分的問題，恰好符合流域河涌水質調查中的復雜性、時變性、困難性的特征[9]。

在針對智能算法的實際應用過程中，由于對河涌流域水質的預測是一個包含多種變量、多個目標、同時涵蓋多個層次的復雜系統，加之所獲取的水環境系統信息不完善，各種參數之間不可避免會出現耦合和關聯的情況，因此本文采用了PCA(Principal Component Analysis)對各過程變量間線性相關關系進行處理，實現輸入數據降維，即輔助變量的精選[10-11]。

當前，對PCA和LSSVM模型建立的研究已經較為成熟，本文僅對建立PVA-LSSVM預測模型的主要步驟進行闡述。

a.原始數據的獲取:通過資料收集和水質實測，整理得到與每條河涌相關的生產廢水入河量、人口數量、農田面積、魚塘面積、初期降雨總凈流量、河涌集雨面積數據，考慮到生活污染源除受人口數量的影響外，還會受是否鋪設截污管道的影響，因此在本文中以人口當量的影響[人口數量×(1-管網覆蓋率)×調整系數計算得到]，同時農業面源污染源以農田面積與魚塘面積之和表示。

b.數據預處理:為更好地提高模型的運行速度，減少運行時間，本文通過算法將步驟a獲得的數據進行歸一化操作，從而使模型的輸入和輸出的數據統計分布大致均勻。

c.利用步驟b中獲得數據，應用PCA算法計算得出主成分的累計方差貢獻率，以較好的擬合水平(本文以累計方差貢獻率不小于90%為要求)確定出主成分個數，組成新的數據樣本矩陣，通過PCA操作可進一步實現數據的精簡。

d.利用步驟c中獲取的新樣本數據，應用LSSVM算法建立起流域河涌水質預測模型；選擇合適的初始參數(包括核函數、核參數和正則化參數)，對上文中的數據進行訓練與測試，直到獲得較好的預測效果。

1.3 基于PCALSSVM和NSGA-Ⅱ的多目標優化模型

在城市水環境整治過程中，需要針對流域河涌不同的情況制定整體系統的治理方案。如何在保證滿足當前水質要求的情況下，設計出具有針對性和合理性的治理方案十分重要。在進行方案設計時，人們往往希望能掌握典型情景下不同污染物輸入對河涌水質的變化影響特征，流域河涌水質預測模型可以很好地幫助人們解決這一問題，但對于同時能夠優化管理、降低運行成本等多目標問題仍需進一步的研究。

NSGA-Ⅱ算法是對基于NSGA(Non-Dominated Sorting in Genetic Algorithms)算法的改進，已經應用于實際中解決多目標優化問題，在處理具有高維數、多模態、非線性等復雜問題上應用廣泛。將前一節建立的PCA-LSSVM流域河涌水質預測模型，代替傳統的數學模型用于NSGA-Ⅱ算法中，可很好地解決NSGA-Ⅱ算法中關于河涌水質預測模型建立困難的問題。

改進的NSGA-Ⅱ算法的基本流程如下：

a.根據多目標問題和約束條件對種群進行初始化。

b.對初始種群進行快速非支配排序，其算法具體步驟如下：對一個初始化種群為P的種群，其每個個體i都有對應的兩個參數ni和Si，其中ni代表種群P中支配i的個體數目，Si則代表被個體i支配的個體數目。第一步，找到種群中不受其他個體影響即ni為0的個體并將其存入到前集合Fi中。第二步，對于集合Fi中的每一個個體j，考察受到個體j即被個體j所支配的個體集Sj，由于個體集中Sj中的個體k已存在于當前集Fi中，因此需要將集合Sj中每一個個體k的nk減去1，如果其值為0，則將個體k存入新的集合H，否則，則保留在集合Sj中。第三步，賦予集合Fi中每一個個體相同的非支配序，并將Fi作為非支配個體集合的第一級，對集合H進行分級排序操作直到所有個體都有其對應的排序值。這樣，集合中所有的個體都進行了分級。

c.確定擁擠度和擁擠度比較算子。在對種群完成快速非支配排序以后，為保證所求得的支配解集分布均勻和種群的多樣性，引入了擁擠度和擁擠度算子。擁擠度是指群體中某一指定點附近包含個體本身但不包含其他個體的最小長方形。通常用Id表示，其計算方法為

對于前集合Fi，n為其包含的所有個體數目，初始化群體中每個個體i的擁擠度為0。即Fi(dj)=0，j代表Fi中的第j個個體。

對于選定目標函數m，進行快速非支配排序操作：

I=sort(Fi，m)

(1)

式中：Fi為集合；m為目標函數。

為確保邊界上的兩個解都能進入下一代，假定每個目標函數處在邊界上的解的擁擠度趨于無窮大：

I(d1)=∞，I(dn)=∞

(2)

式中：I(d)為個體擁擠度。

則其余個體的擁擠度為

(3)

式中：k為第k個個體。

經過以上排序和擁擠度計算，種群中每個個體都具有非支配序和擁擠度兩個屬性。

d.根據種群個體的非支配序和擁擠度進行篩選工作，其評價準則為：當兩個個體的非支配排序不同時，非支配排序更高的被篩選出來；當非支配排序相等的兩個個體進行比較時，選取擁擠度更小即周圍不擁擠的個體。根據錦標賽選擇策略，重復進行篩選工作直到達到最大種群規模。

e.基因操作。為避免算法陷入局部最優的情況，NSGA-Ⅱ算法選擇交叉變異操作，包括基因的重組和變異操作。通過模擬二進制交叉(SBX)基因重組使得到的子代個體能夠保留兩個父代個體中的模式信息。其子代具體產生過程如下：

(4)

(5)

式中：ci,k為交叉產生的子代，pi,k為其父代，βk≥0，為種群的任意一個個體。

概率密度函數為

(6)

(7)

可由式(8)、式(9)導出：

(8)

(9)

NSGA-Ⅱ算法基因變異產生子代主要是靠多項式變異算子(PM)實現的，其操作過程為

(10)

式中δk可由式(11)、式(12)求得：

(11)

(12)

式中：rk為個體的非支配排序；ηm為變異分布指數。

f.模擬二進制交叉和多項式變異產生的種群與原種群合并形成新的種群，通過篩選進一步形成新的種群直到當前進化代數達到最大進化代數，輸出最終種群的非支配個體，見圖2。

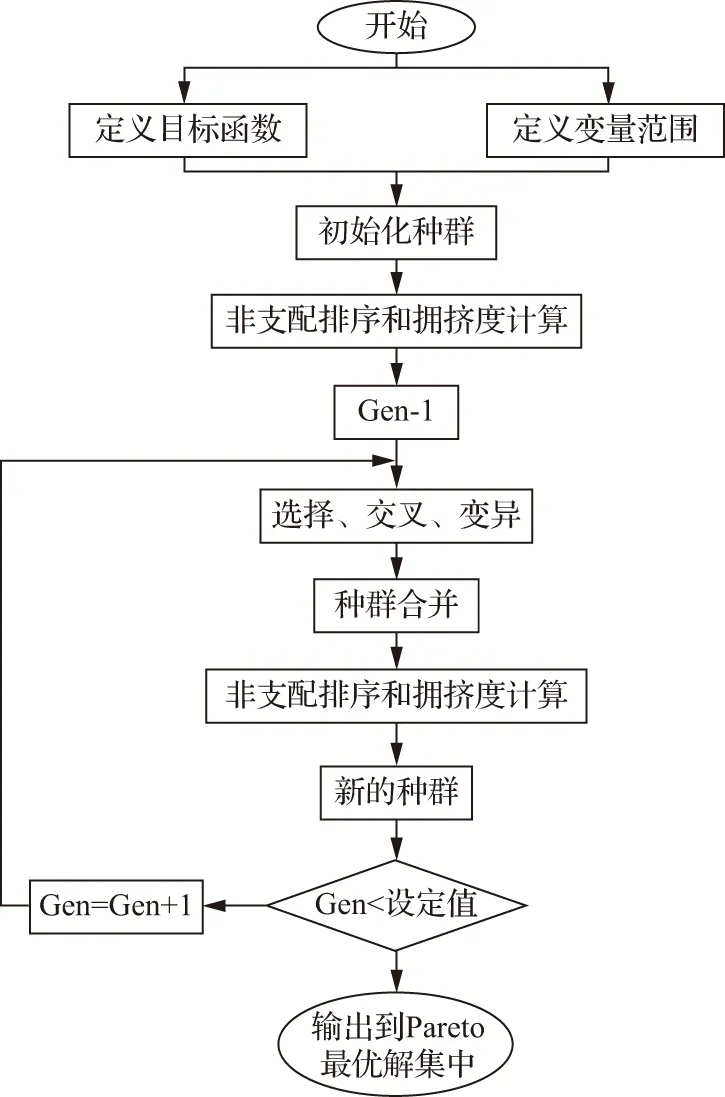
圖2 優化模型流程示意

1.4 原始數據的采集及PCA處理

本文收集得到中山市南朗流域13條黑臭河涌(北部排洪渠、中心二河、泮沙排洪渠、蘭溪河、大溪、麻子涌、南沖渠、貝里坑、白企坑、合水坑、大車南渠、大車北渠、東椏涌)相關數據。選取的模型輸入量包括人口當量、農業面源面積、生產廢水入河量、初期降雨總凈流量4項外部污染源變量和河涌集雨面積1項河涌自身影響變量，算法模型的輸出變量為河涌實測水質高錳酸鹽指數和溶解氧濃度。

在進行模型訓練前，為消除不同量綱的影響，首先對獲得的數據進行歸一化處理：

(13)

式中：S(i)為數據集中的一組數據；max(S)為數據集中最大的一組數據；min(S)為數據集中最小的一組數據。

經歸一化處理后的數據利用PCA算法進行降維操作，本文所有算法運行均在MATLAB 2015b軟件環境下運行。PCA算法處理結果如圖3、圖4所示，圖3中連接原點與各變量的直線的“向量”可顯示輔助變量與樣本點之間的多元關系，具體的向量在某一主成分上的投影可表明該變量對該主成分的重要程度，投影矢量長度越大，代表該向量的重要程度越高，該主成分對該變量的解釋程度也越高[13]。從圖3雙標圖中變量的矢量長度可以看出，外部污染源中人口當量、初期降雨總凈流量和生產廢水入河量是十分重要的影響變量，河涌自身影響變量集雨面積也十分重要，農業面源面積影響較小。從圖4可以看出，第一主成分的方差貢獻率為73.13%，對變量的解釋程度一般，第二主成分的方差貢獻率為15.19%，與第一主成分的累計方差貢獻率為88.32%，對變量的解釋屬于中等偏上的水平，第三主成分的方差貢獻率為7.28%，前三主成分的累計方差貢獻率為95.60%，有很好的擬合度水平。

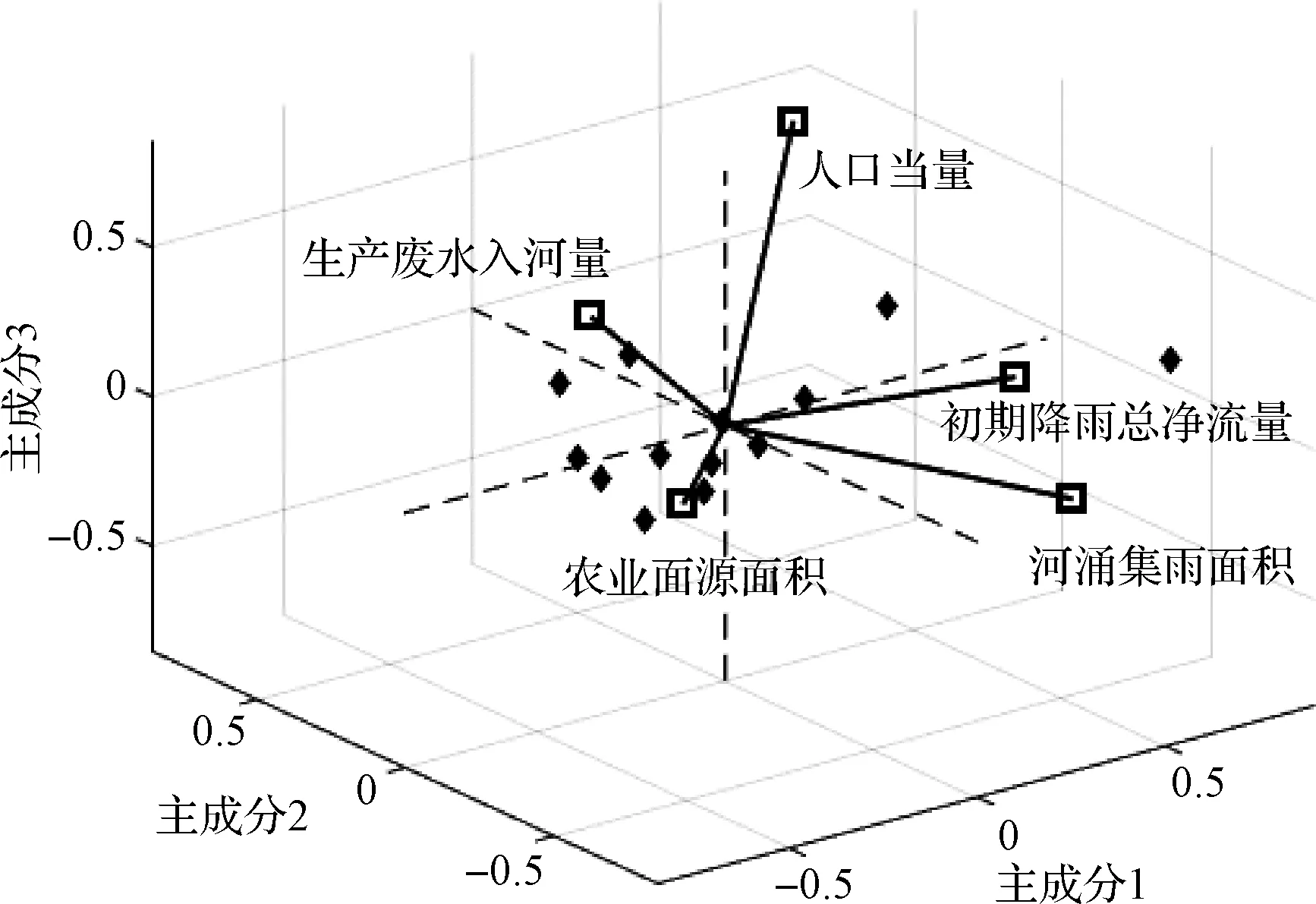
圖3 雙標圖

圖4 各主成分方差貢獻率結果

為進一步對此次流域河涌水質模型預測性能的好壞進行量化，本文分別選取均方根誤差(RMSE)和相關系數(R)對模型的預測性能進行表征。其中RMSE值越小，R值越接近于1，說明模型的水質預測值與河涌水質的實際值的相關度越高，代表模型的預測性能越好[14-15]。

2 結果與討論

2.1 PCA-LSSVM模型預測仿真

結合PCA-LSSVM模型的河涌水質高錳酸鹽預測模型和溶解氧水質預測模型進行仿真。其中，輸入層為人口當量、農業面源面積、生產廢水入河量、初期降雨總凈流量和河涌集雨面積，輸出層分別為河涌水質高錳酸鹽指數和溶解氧，使用Matlab2015b中LSSVM工具箱編寫程序建立河流水質預測模型，選取徑向基函數(RBF)作為核函數，算法初始化正則化參數γ和核參數σ2的取值范圍為：γ∈(0，1000),σ2∈(0，100)。通過網格搜索法和10倍交叉驗證法最終選出的正則化參數和核參數的最優值分別為γ=35.2606和σ2=5.7196。仿真結果見圖5、圖6和表2。

從圖5、圖6中可以看出，基于PCA-LSSVM模型的河涌水質模型中高錳酸鹽指數和溶解氧預測值與實際真實值基本趨同；由表2可知，訓練數據樣本中高錳酸鹽指數預測值和真實值之間的均方根誤差為5.11，預測數據與實際數據的相關系數為0.8290；而對于溶解氧而言均方根誤差為1.65，模型預測數據與河涌水質實際數據的相關系數為0.8126。兩模型的預測數據與河涌水質實際數據的相關系數都在0.8以上，屬于較好的預測水平。盡管兩個模型都存在部分數據的偏離，但總體預測效果較好，這表明LSSVM具有很好的預測能力和非線性映射能力，能夠作為NSGA-Ⅱ的目標函數。

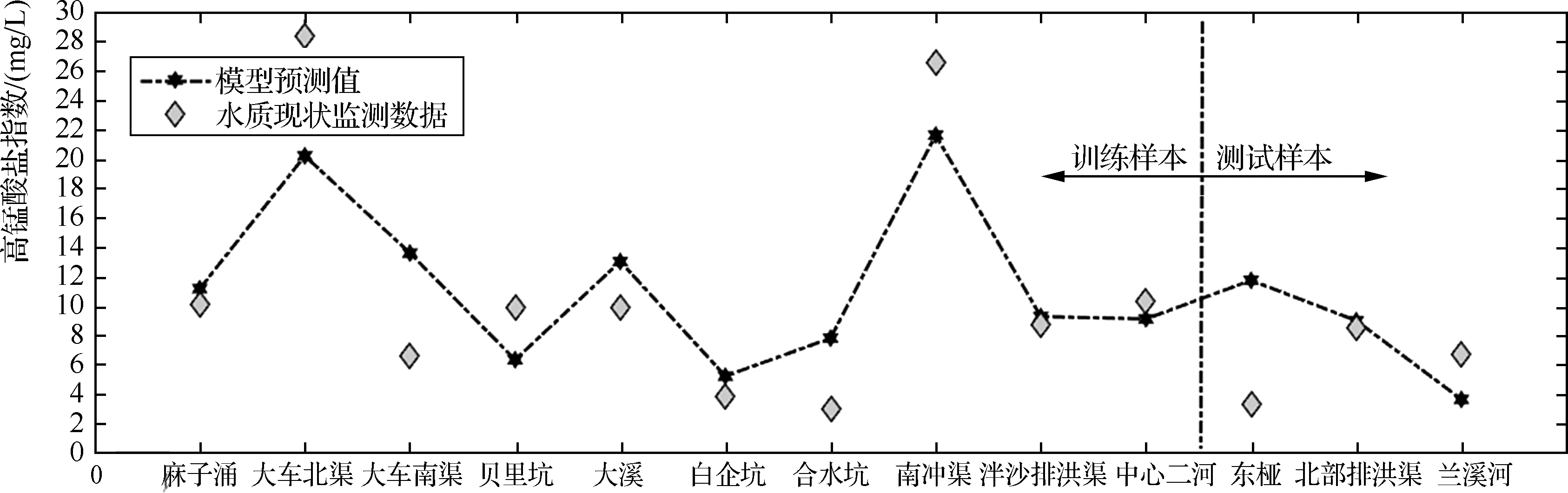
圖5 PCA-LSSVM模型對高錳酸鹽指數仿真結果

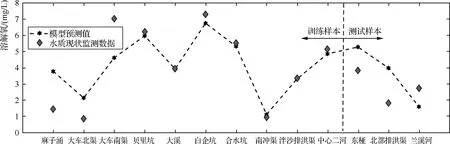
圖6 溶解氧仿真結果

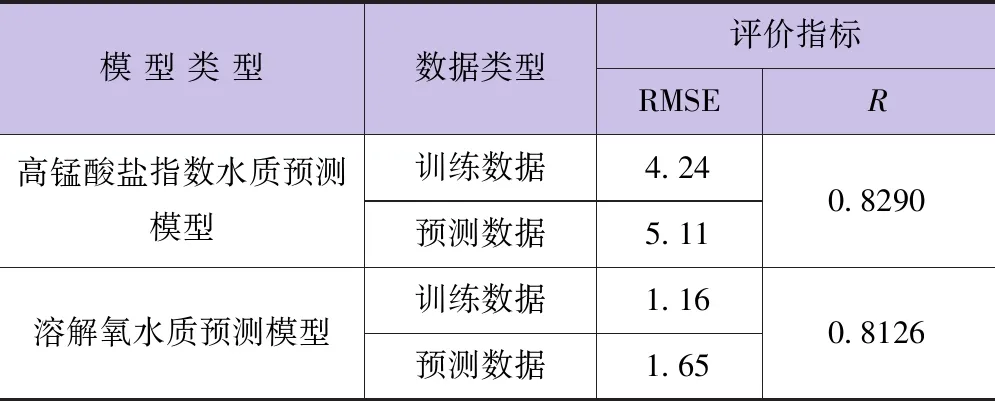
表2 模型預測性能

2.2 基于PCA-LSSVM和NSGA-Ⅱ的多目標優化的實現

采用PCA-LSSVM智能算法的河流水質預測模型能夠較好地模擬出各參數輔助變量與優化目標量之間的關系，鑒于該模型選用輸入量人口當量、農業面源面積、生產廢水入河量、初期降雨總凈流量和河涌集雨面積中包含了一部分不可控量(初期降雨總凈流量和河涌集雨面積量)，為避免優化過程中其值被當作可變因素影響模型輸出，在本節中我們采用人口當量、農業面源面積、生產廢水入河量3項參數，利用PCA-LSSVM 建立新的河涌水質預測模型，同時將該模型代替傳統的數學模型用于NSGA-Ⅱ算法中解決城市水環境綜合整治決策過程中的多目標優化問題。在滿足水質目標要求的前提下，探尋不同污染源變量之間與河涌水質之間的關系，最終建立起基于PCA-LSSVM和NSGA-Ⅱ相結合的多目標優化模型。優化模型為目標函數：

f1(CCod)=sim(net1,[人口當量,農業面源面積,生產廢水入河量]

f2(DO)=sim(net2,[人口當量,農業面源面積,生產廢水入河量]

(14)

(15)

式中：為保持預測的準確性，約束條件的選擇范圍依據預測模型的取值范圍；net1，net2分別為基于PCA-LSSVM算法建立的高錳酸鹽和溶解氧預測模型。進一步選取NSGA-Ⅱ 參數為：種群數量100、交叉概率0.4、變異概率0.05、最大進化代數1000。優化結果見圖7。

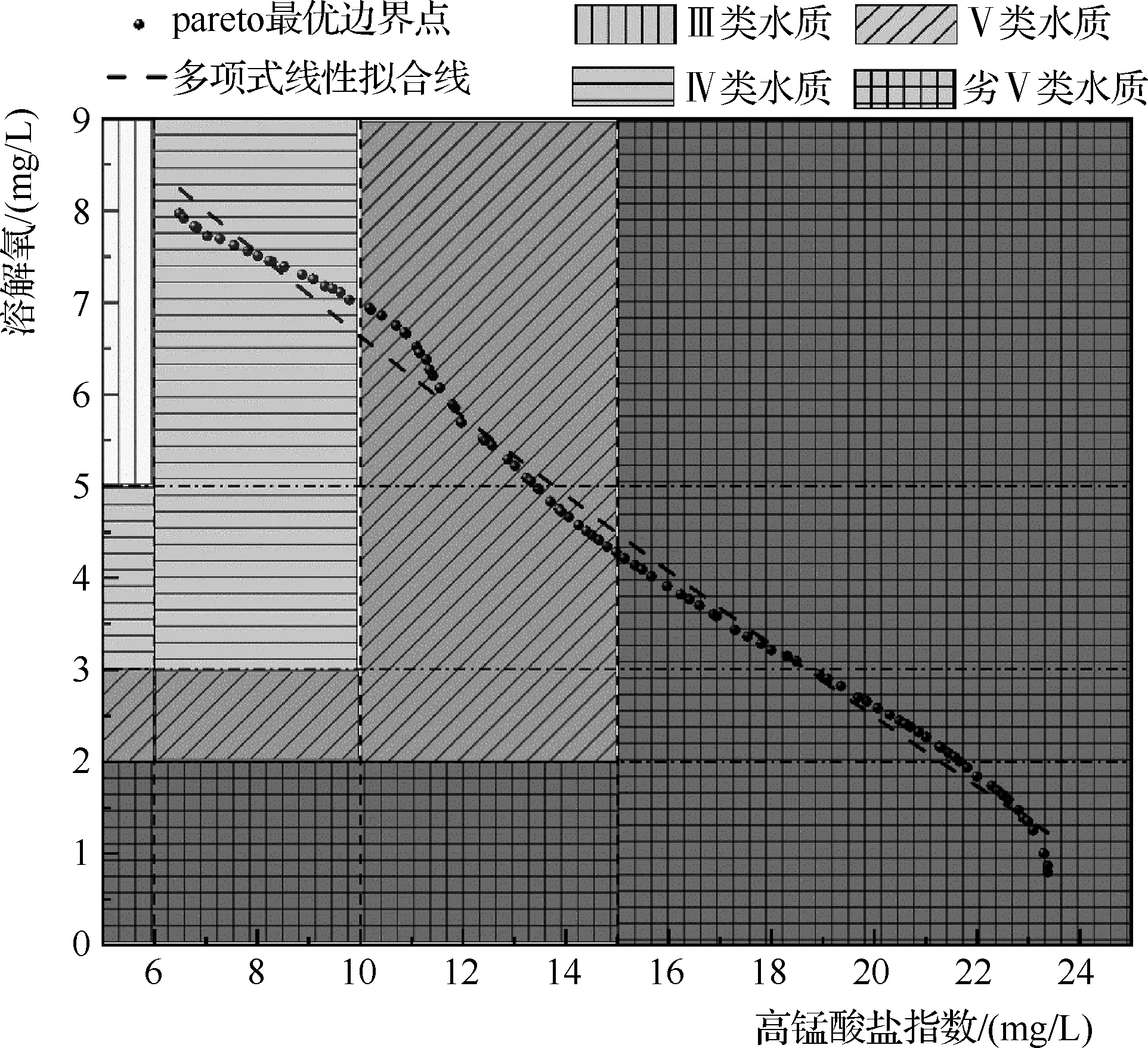
圖7 優化模型運行結果

由圖7中Pareto最優邊界點的軌跡可以看出，高錳酸鹽指數和溶解氧之間存在或有這樣的關系：隨著河涌水質中高錳酸鹽濃度的升高，水質中溶解氧濃度下降，反之亦然。進一步地，從數學模型的角度解釋預測模型中高錳酸鹽指數和溶解氧之間的相關關系，運用Matlab的聚類多項式線性擬合工具對圖中的曲線進行擬合，擬合后，河流水質高錳酸鹽指數和溶解氧的聯系可以用二次多項式表示為

Y=11.38681-0.50521X+0.00302X2

(16)

相關性系數為0.99111。

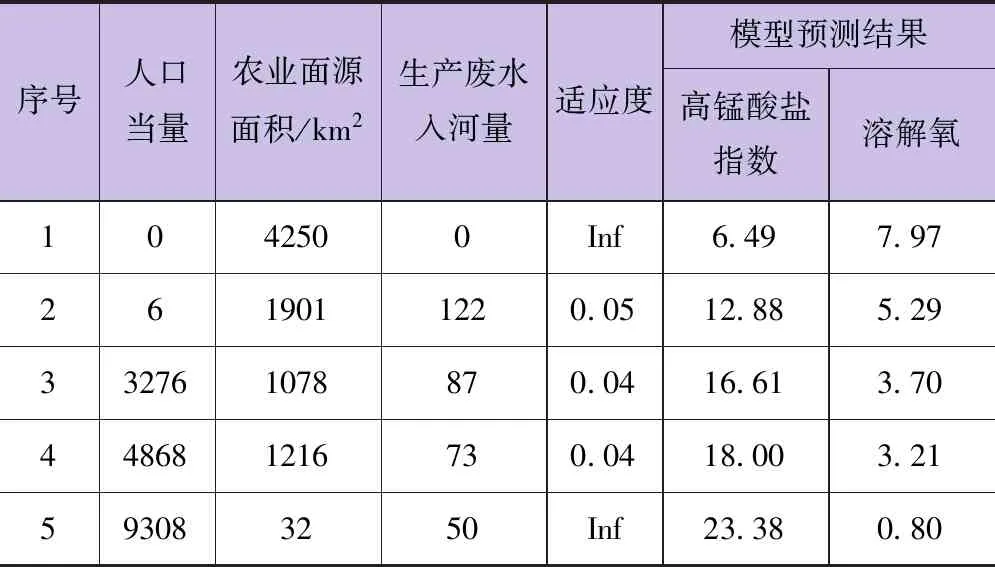
表3 部分最優邊界點參數

表3給出了部分Pareto最優邊界點。從表中可以看出，人口當量，即生活污水入河量對水質影響較最明顯。圖8給出了目標迭代過程中人口當量、農業面源面積、生產廢水入河量的分布。從圖8中可以看出，人口當量對河流水質的影響最為明顯，表現為高錳酸鹽指數之間有較明顯的規律：當人口當量較少(接近于0)時，農業面源污染較高(農業面源面積較大)，河涌水質高錳酸鹽指數隨生產廢水入河量升高而上升。盡管農業面源面積和生產廢水入河量保持下降的態勢，但當人口當量增加時，河涌水質高錳酸鹽指數仍然有明顯的上升勢態。可見在區域流域的水環境綜合治理中，決策方案的制定應該重點關注對居民生活污染源的治理，采取對應的截流措施以達到較好的治理效果，同時考慮工業污染源、農業面源及其他污染源的影響。

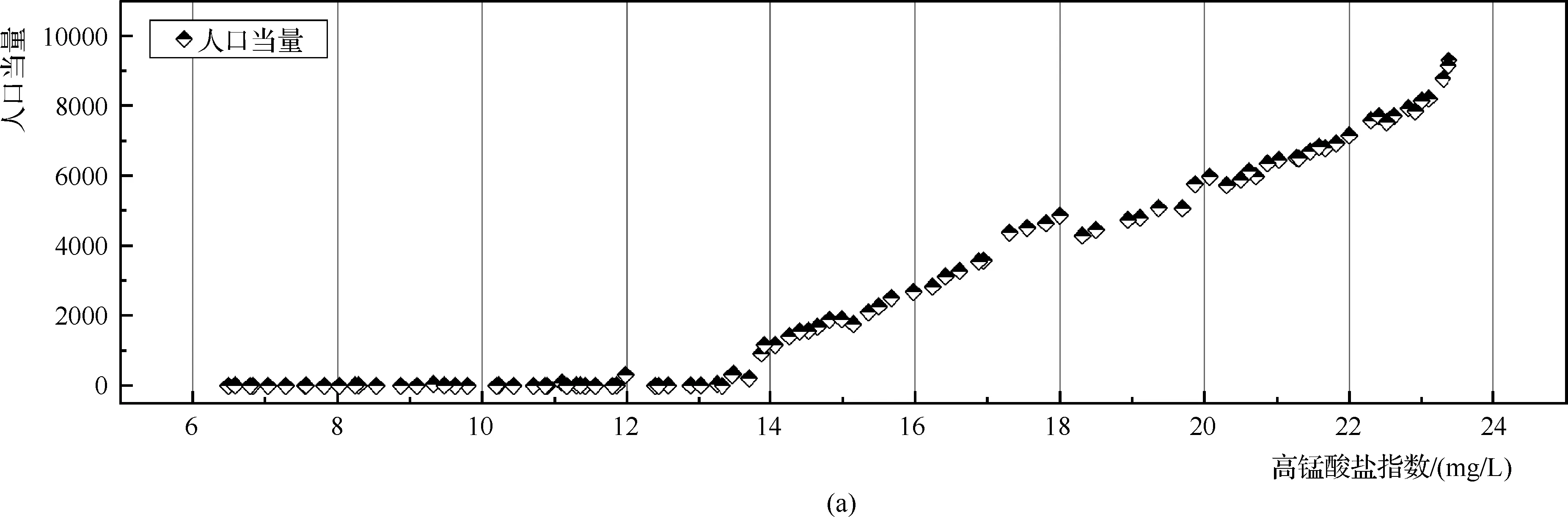
圖8 Pareto最優邊界中各變量分布

3 結 論

a.建立城市水環境綜合整治過程中的多目標優化模型。本文通過資料收集和文獻查閱等方式共得到南朗流域13組河涌水質組元數據。實驗模型選取人口當量、農業面源面積、生產廢水入河量、初期降雨總凈流量和河涌集雨面積5項輸入變量，河涌水質實測數據高錳酸鹽指數和溶解氧作為模型輸出變量。

b.針對城市水環境綜合整治決策過程中的多目標優化問題，通過多種混合智能算法，成功建立起基于PCA-LSSVM的河流水質高錳酸鹽指數和溶解氧預測模型，模型測試數據與實際數據的相關系數分別為0.8290和0.8126。基于PCA-LSSVM混合智能算法的河流水質預測模型也可為入河支流對主河道的污染預測提供參考。

c.為解決城市水環境綜合整治決策過程中的多目標優化問題，利用NSGA-Ⅱ算法建立了優化模型，優化結果表明，在區域流域的水環境綜合治理中，決策方案的制定應該重點關注對居民生活污染源的治理，同時考慮工業污染源、農業面源及其他污染源的影響。可為解決城市水環境綜合整治方案的設計和操作提供參考和指導。