新型負剛度吸能結構力學特性分析1)
侯秀慧 呂 游 周世奇 朱志韋 張 凱 鄧子辰
(西北工業大學力學與土木建筑學院,西安 710129)
(復雜系統動力學與控制工業和信息化部重點實驗室,西安 710072)
引言
在沖擊載荷作用下,吸能材料的應用具有重要的工程意義.傳統的減振吸能方法主要有兩種:其一,利用材料的塑性變形實現能量吸收耗散[1],如汽車保險杠和輕型自行車頭盔均是基于這一原理進行結構以及超材料設計,然而破壞性的塑性變形使得材料無法重復利用;其二,利用材料的黏彈特性[2-3],實現重復性的能量吸收,如橡膠鞋底和汽油活塞減振器等都是基于材料黏彈性理論實現的能量吸收,但這種情況下的吸能效果嚴重依賴于加載和卸載的速度.工程中理想的減振吸能材料顯然需要滿足如:可重復使用、輕質、自主耗能、持續吸能等特點[4-5].近幾年,基于多孔結構輕質高強等優異的力學性能[6-11],利用多孔結構的負剛度特性實現自主耗能,受到國內外學術界的廣泛關注[12-16].
Qiu 等[17]設計出一種“雙曲梁”雙穩態結構,這種新型多孔結構不依賴于預應力即可實現雙穩態屈曲變形;模態分析以及有限元模擬結果表明:該結構的雙穩態特征取決于曲梁的截面尺寸以及曲率的大小.Restrepo 等[18]通過設計具有“柔性雙穩態機構”的曲梁單胞,引入解析模型分析了PXCM(phase transforming cellular materials)材料的本構行為,研究表明PXCM 的漸進相變產生了加載?卸載的滯回環現象,從而實現了能量吸收;PXCM 的這種吸能特征不僅可與金屬及聚合物蜂窩結構的吸能能力相媲美,而且其變形是可恢復的.但由于結構存在多穩態,每次使用后都將借助外力恢復初穩態才能再次使用,在使用效能上嚴重受限.Findeisen 等[19]提出了由雙穩態曲梁單元組成的三維晶格結構,通過半解析以及有限元方法對該三維力學超材料進行穩定性分析,研究結果表明:區別于以往依靠材料的破壞性塑性變形以及黏彈性耗能,該超材料能量耗散主要是將外部沖擊載荷的沖擊能轉化為超材料結構的振動,令其變形具有可重復、可恢復以及可設計性等特征.Pan 等[20]通過設計三維 PM(pixel mechanical)結構,利用自我反彈的負剛度特性實現減振耗能.
結構產生振動的主要原因是外部沖擊載荷的能量(動能)輸入,如要迅速減小沖擊載荷引起的結構振動,可通過增大結構彈性變形(加載?卸載)過程中吸收的能量來實現.負剛度結構的吸能能力,主要取決于負剛度單胞臨界載荷最大值與最小值的差值,如圖1 所示,然而對于大多數不具雙穩態的負剛度結構,其負剛度臨界載荷最大與最小值間的差值較小,能量吸收效果不明顯,結構將出現彈性應變能與動能的反復轉換,從而出現持續性的振動.而具有雙穩態特征的負剛度結構雖然具有較強能量吸收效力,但因其不能自主反彈,無法實現持續性的吸能,當被壓實后,結構也將出現持續性的振動.為了有效地解決這一問題,本文通過負剛度超材料構型設計,利用具有多穩態特征的曲梁作為單胞的胞壁,通過單胞構型控制,在抑制結構多穩態出現的同時,提高結構負剛度臨界載荷最大值與最小值的差值,從而實現結構吸能效率的提升,加快能量的衰減,減小載荷引起的持續性振動.
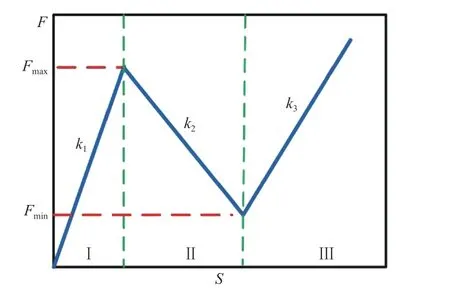
圖1 負剛度單胞力(F)?位移(S)曲線示意圖Fig.1 Sketch of force (F)-displacement (S)relation for a negative stiffness cell
本文提出了一種由曲梁單元增加約束(在曲梁中點增加豎向柱、在曲梁兩端點增加側壁、在曲梁底部進行凹槽設計)所構建的新型三維負剛度結構,并研究了其在沖擊載荷作用下的吸能特性.與已有的單穩態負剛度結構相比,該新型結構通過增加約束抑制曲梁多穩態的出現,同時通過彈性范圍內曲梁大變形壓縮過程中內部單元的自主回彈,實現了結構吸能效率的提升.采用數值模擬方法分析了單胞幾何參數,結構周期性對屈曲模態以及吸能效率等力學性能的影響,同時進行了梯度結構設計,并解析其在不同沖擊載荷下能量的吸收效率,為工程結構減振耗能提供技術支持.
1 分析模型
1.1 負剛度結構吸能特性分析
負剛度結構,也稱為負剛度超材料,通常定義為由具有負剛度行為的單胞組成的結構.對于傳統結構,其沿外力方向的變形隨載荷增大而增大,而負剛度單胞表現出相反的行為,即變形隨著載荷的減小而增大,如圖1 所示,力?位移曲線在負剛度行為區間存在最大值Fmax和最小值Fmin,若最小值小于0,結構存在雙穩態,在壓縮后將無法反彈至最初形態;若最小值大于0,結構不存在雙穩態,在壓縮后將能自主恢復到最初形態.由多個負剛度單胞組成的負剛度結構的加載?卸載力?位移曲線如圖2 所示,由圖2 可知,加載?卸載滯回曲線存在一個封閉的區間,該區間面積即為負剛度結構一個加載?卸載周期吸收的能量.曲線是周期性的,且其最大值和最小值隨串聯的負剛度單元個數增加而分別收斂于負剛度單胞的臨界載荷最大值與最小值.在Fmin>0 的情況下,負剛度結構之所以能夠實現自主回彈,這是因為串聯的負剛度結構在受到壓縮載荷時,由于制造缺陷,結構會出現某一層先到達負剛度臨界值點,該層單胞結構會繼續壓縮而其他層單胞回彈,導致這種回彈的原因為[18]:由圖1 所示,負剛度單胞的剛度變化呈現出3 個階段,即k1→k2→k3.設負剛度結構單胞串聯個數為n,壓縮過程中處于3 個階段的單胞個數分別為n1,n2,n3.結構壓縮過程中的有效剛度可表示為
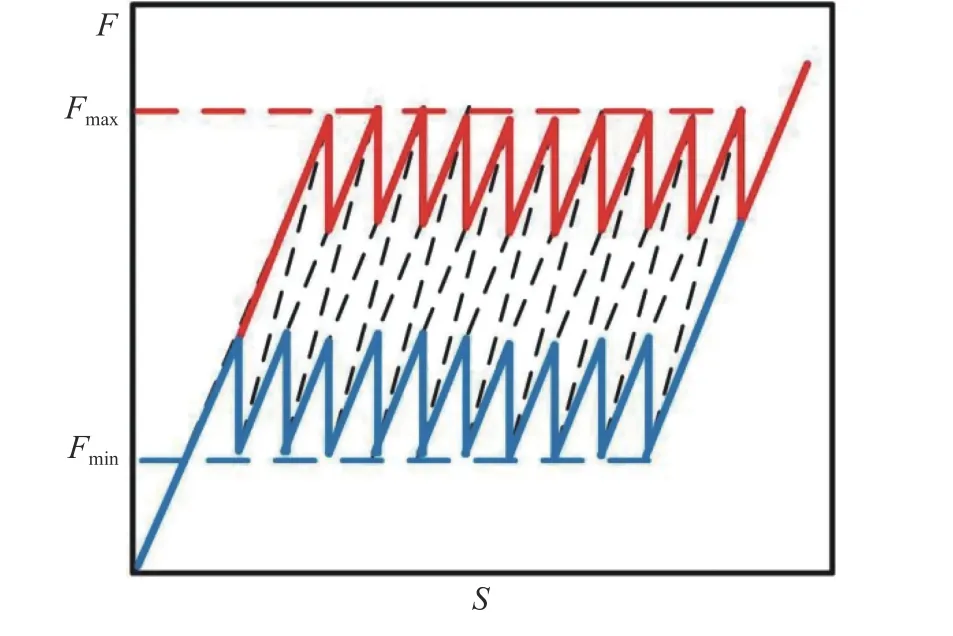
圖2 負剛度結構力(F)?位移(S)曲線示意圖[1]Fig.2 Sketch of force (F) -displacement (S)relation for a negative stiffness structure[1]

這表明在結構上增加單胞個數會降低結構的有效剛度.假設結構壓縮過程只某一行單胞處于負剛度階段,則處于第Ⅰ和Ⅲ階段結構部分的有效剛度隨n值增大而減小,而處于第 Ⅱ 階段的部分剛度(其只有一行)保持不變為k2,當n達到或超過某一臨界值時,滿足條件
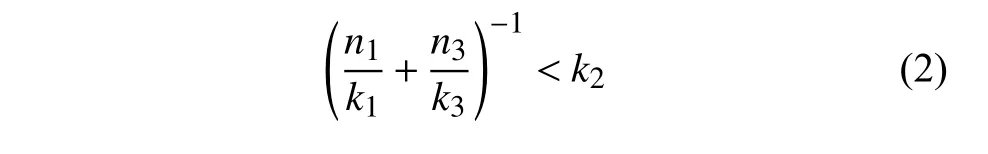
結構將表現出回彈行為,即位移的反轉以及驅動轉換所需平衡力的減小導致的回彈行為;同樣,卸載過程中,結構某一層將先達到負剛度臨界載荷值的最小值點,該層單胞會出現回彈而其他層單胞發生壓縮變形.由于加載?卸載過程中內部單胞的自我調整和回彈振動消耗能量,使其儲存在單元內部的部分彈性應變能在回彈過程中被消耗,從而實現耗能,并且克服了雙穩態吸能結構借助外力恢復變形才能再次使用的弊端,這一特性已被用于相關結構吸能設計[21-22].
1.2 單胞構型設計
本文以如圖3(a)所示曲梁為基本組件,設計出三維單胞構型如圖3(b)所示,其中曲梁初撓度設為兩端固支直梁的第一階屈曲模態,即

圖3 曲梁組件及三維單胞Fig.3 Curved beam module and 3D unit cell

其中,h為曲梁的初始頂點高度,L為梁的跨度,t為曲梁壁厚度,t1為側壁厚度.定義Q=h/t為曲梁的形狀因子.
當曲梁兩端受固定約束時,在曲梁跨中頂點處施加外載荷f,采用模態疊加法并忽略高階模態,可得到如下封閉解[17,23]:若二階模態未被限制

若二階模態受到限制

參數無量綱化
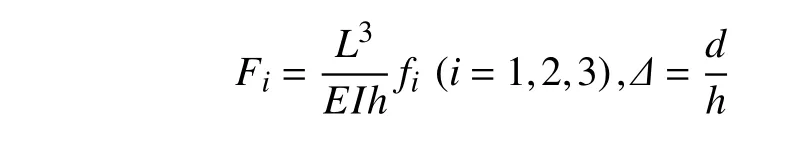
其中,E為材料彈性模量,I為截面慣性矩,d為曲梁頂點A的位移.
由式(4)~ 式(7)可得曲梁頂點作用載荷時的力?位移曲線,如圖4 所示.可得:只具有負剛度而不具多穩態的曲梁 (Q<2.31),其負剛度臨界載荷最值間差值較小;而具有多穩態的曲梁(Q>2.31),其負剛度臨界載荷最大與最小值間的差值較大.而負剛度結構一個周期內能量吸收值的大小取決于負剛度臨界載荷最大值與最小值的差值(見圖2),因此利用構型設計,使曲梁Q>2.31 的同時,通過在單胞頂點增加高為h/2 的豎向柱,抑制曲梁二階模態的出現,從而提高負剛度單胞臨界載荷最大值Fmax(即式(7)對應的F3).同時通過在曲梁底部進行凹槽設計,以抑制曲梁在Q>2.31 時多穩態的出現,從而形成如圖3(b)所示的三維負剛度單胞.該結構將增大負剛度臨界載荷最值間的差值,實現結構的完全自主反彈和減振耗能能力的提升.

圖4 歸一化的曲梁力?位移關系的幾種解[17]Fig.4 Several solutions of the normalized force-displacement relations of curved beams[17]
2 力學性能參數分析
以金屬鋁(E=68 GPa,ρ=2300 kg/m3)為基底材料,取如圖3(b) 所示三維單胞的一部分,用ABAQUS 有限元軟件分析側壁厚度t1對屈曲模態的影響.由于結構具有大變形,采用了動力顯示分析步,并且考慮幾何非線性,采用修正的二次四面體單元,即C3D10M 單元,該非線性積分單元具有10 個節點,分別位于四面體的4 個頂點和6 條邊中點,每個節點具有3 個自由度,在位移控制下,能夠捕捉到后屈曲以及負剛度單元的跳躍現象,可以避免剪切和體積自鎖,適用于ABAQUS/explicit 分析步下大變形和接觸問題的分析.邊界條件設置上,單胞底部為完全固定,將單胞頂部耦合到一參考點,并輸出該參考點在加載過程中的力?位移曲線.選取的分析模型如圖5 所示,其中圖5(a)側壁厚度t1=2t,圖5(b)側壁厚度t1=t.已知兩端固定的曲梁,在二階模態受到抑制時,其在頂點載荷的作用下,產生的屈曲模態如圖6 所示.通過對比可知,當側壁厚度取 2t時,側壁相對剛度較大,單胞壓縮過程中產生與固端約束相同的屈曲模態,且引起較大的負剛度臨界載荷最大值,如圖7 所示;同時由于單胞凹槽底部胞壁的限制,負剛度臨界載荷最小值大于0,從而使多穩態單胞結構能夠實現自主反彈.而對于圖5(b),由于單胞側向壁厚與曲梁壁厚大小相當,從而使側壁相對剛度較小,不足以限制曲梁的轉動,因此側向胞壁產生較大轉角,出現了與兩端固定的受壓曲梁不同的屈曲模態,且其負剛度臨界載荷最大值與固端屈曲模態相較,有明顯減小,如圖7 中實線所示.

圖5 側壁厚度 t1 對曲梁屈曲模態的影響Fig.5 Effect of lateral wall thickness t1 on the buckling mode of curved beam

圖6 兩端固定曲梁在二階模態受到抑制后的屈曲模態Fig.6 Buckling mode of a curved beam fixed at both ends after the second-order buckling mode being suppressed

圖7 不同側壁厚度(t1)下單胞的力(F)?位移(S)曲線Fig.7 Force (F)-displacement (S) relation of the unit cell with different lateral wall thicknesses (t1)
由此可知,當側壁厚度相對曲梁壁厚較大時(t1≥2t),可將其視為曲梁端點的固端約束,在高為h/2的豎向柱的作用下,曲梁的二階模態受到抑制,從而產生如圖6 所示的屈曲模態.
針對相對壁厚(側壁與曲梁的壁厚比值t1/t)的臨界值,進行了理論及有限元分析,即探討在何種側向壁厚條件下,可以獲得如圖6 所示的屈曲模態.在曲梁頂點施加外載荷f,側向胞壁將會受力彎曲,其中側向胞壁底端的彎矩大小為
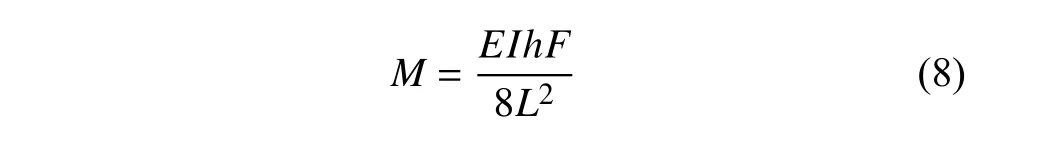
其中I=bt3/12 為曲梁胞壁的截面慣性矩.
在該彎矩作用下,側向胞壁相對豎直方向轉角為
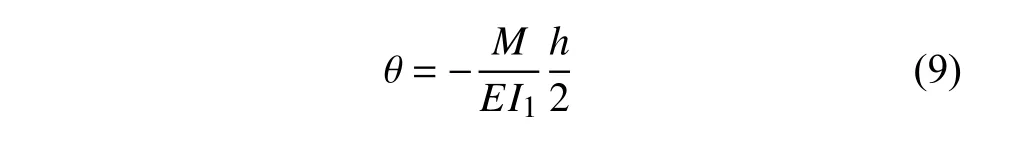
其中I1=/12為側向胞壁的截面慣性矩,b為側向胞壁平面外厚度(設為常數).
將式(8)代入式(9),可得
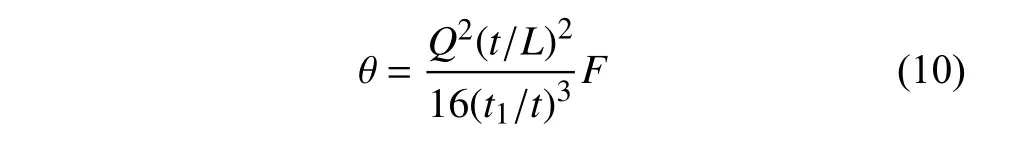
由式(10)可知,端部受約束的曲梁結構的屈曲模態由除外載f之外的結構幾何參數Q=h/t,t/L,t1/t所決定.
用有限元軟件模擬不同Q,t/L,t1/t取值下曲梁的屈曲模態,從而確定側向胞壁對曲梁端點的約束效果,如圖8 所示.在兩種情況下,結構會呈現出固端屈曲模態:
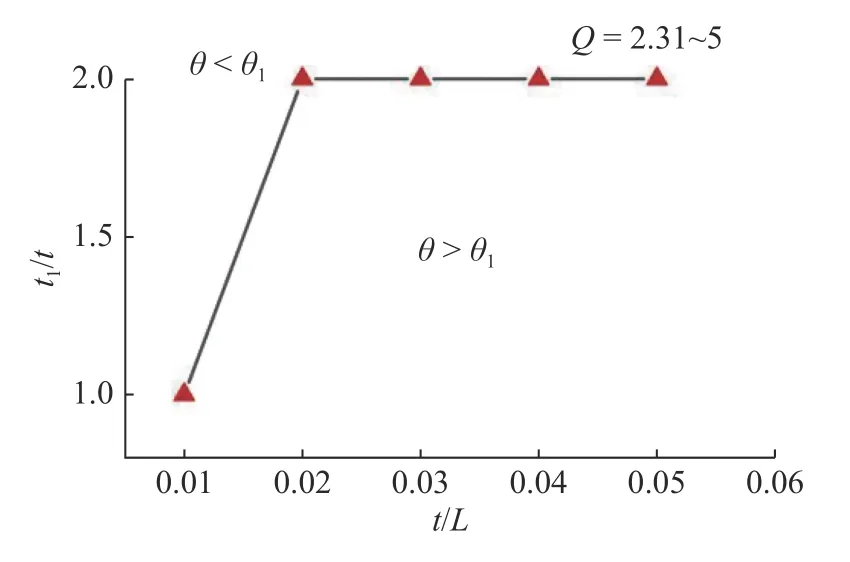
圖8 Q, t/L,t1/t對結構屈曲模態的影響(θ1 為t1=2t 時側向胞壁相對豎直方向的轉角)Fig.8 Effects of Q, t/L,t1/t on buckling modes of the new developed structure (θ1 represents the angle of the lateral wall relative to the vertical direction when t1=2t)
(1)當t/L<0.01 且t1/t>1時,即曲梁壁厚t相對曲梁長度L較小,而側向壁厚t1大于曲梁壁厚t時,θ<θ1,其中 θ1為t1=2t時側向胞壁相對豎直方向的轉角.
(2) 當 0.01
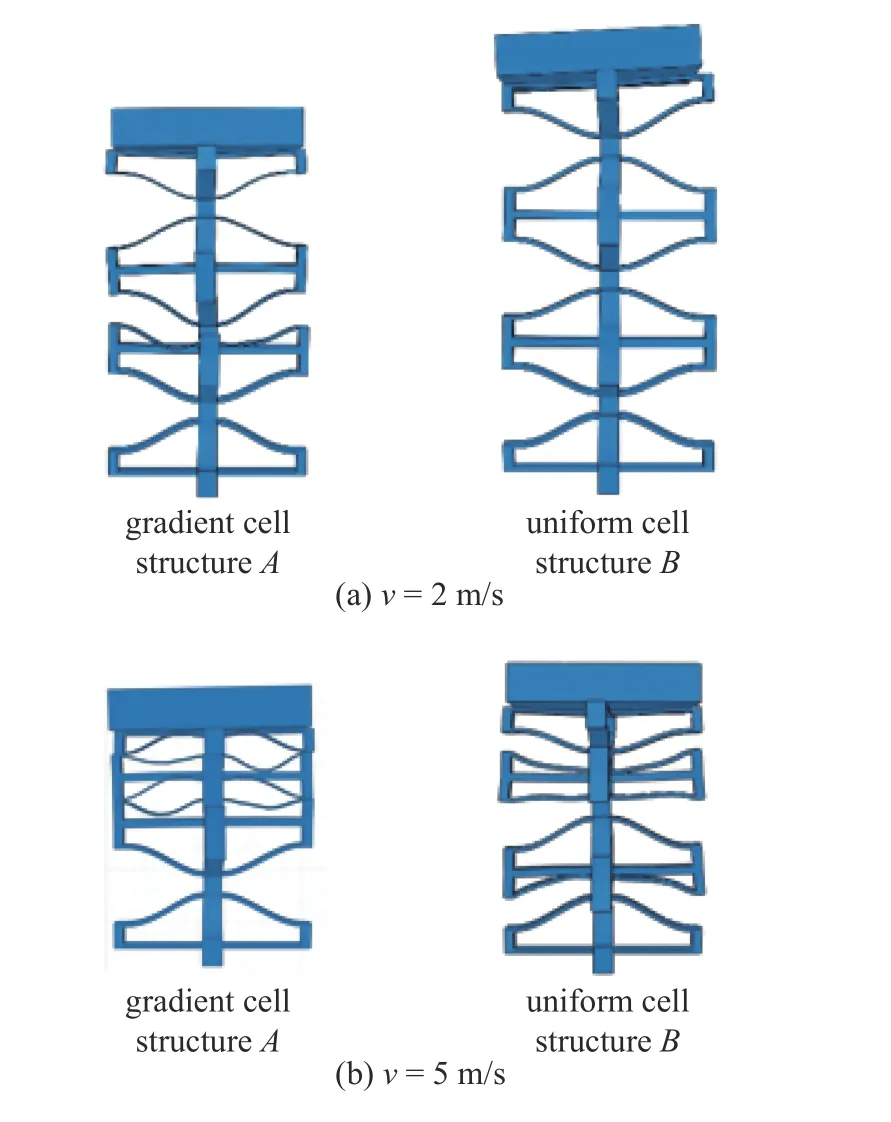
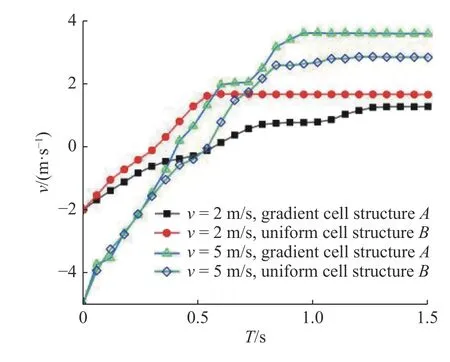
形狀因子Q的影響,由圖8 可知,當形狀因子2.31 隨著單胞串聯個數的增加,負剛度結構的耗能比也會逐漸增大.當串聯的單胞數量足夠多時,結構整體的耗能比最后趨于一個穩定的值,并且在加載?卸載過程中,結構所受載荷趨近于單胞負剛度臨界載荷的最值.本文通過理論解析,利用單胞加載?卸載的力?位移響應計算單胞吸收的能量大小,并比較了不同參數對單胞吸能效率的影響. 單胞單位質量吸收的能量可表示為[24] 其中,W為單胞吸收的能量,s為最大位移,ρ 為基底材料的密度,V為單胞的體積,f1(δ)與f2(δ) 分別為結構加載?卸載過程中變化的外力值.V可以通過將單胞凹槽胞壁體積Vwall和曲梁體積Vbeam相加得到,曲梁的體積Vbeam的計算方法是將曲梁的長度,曲梁平面外厚度b及曲梁面內壁厚t相乘.其中通過對曲梁形狀的線性函數w(x) 積分得到曲梁的長度. 在加載?卸載過程中,當單胞個數足夠多時:f1(δ)?f2(δ)=fmax?fmin其中fmax,fmin由式(6)與式(7)聯立求解.在這種情況下,計算了不同Q,t/L下曲梁單胞吸收的能量大小.其中曲梁I 相應參數為 曲梁II (要求Q(II)>2.31,此處取Q(II)=5),相應參數為 在不同t/L值下,曲梁I (Q(I)=2.31) 和曲梁II(Q(II)>2.31)單位質量的能量吸收大小如圖9 所示.結果顯示曲梁II 的吸能效果比曲梁I 有大幅度提高,且隨著曲梁相對壁厚(t/L)的增大,該負剛度結構吸收能量的能力迅速增強,這是因為此單胞負剛度臨界載荷最大值是壁厚t的三次方,在相同Q值下,不同t/L對單胞吸能大小有顯著影響.定義曲梁I (Q(I)=2.31)單位質量能量吸收值(Wm1) 與曲梁II (Q(II)>2.31)單位質量能量吸收值 (Wm2) 的比值為η=Wm1/Wm2,如圖10 所示.在相同t/L值下,η值將隨著Q(II)值的增大而減小,但是不同t/L值的變化對 η 無顯著影響,這是因為在相同t/L值下,Q值對結構質量和體積影響很小,單胞結構吸能比值大小主要取決于Q值對負剛度臨界值的影響.由圖9 和圖10 的對比分析可知,本文所設計的三維曲梁結構(曲梁II)在實現自主反彈的基礎上,吸能效率得到了顯著提升. 圖9 不同 Q 值下,結構吸收的能量隨 t/L 的變化關系Fig.9 Variation of energy absorption Wm with t/Lunder different shape factorsQ 圖10 單胞吸能比值 η 隨形狀因子 Q(II) 的變化關系Fig.10 Variation of energy absorption efficiencyη with different shape factorsQ(II) 為進一步驗證上述結果的正確性,采用Q=5,h=0.1 m,L=1 m,t=0.02 m的單胞,并將該單胞按照 3×3和6×6 的排列方式組成周期結構,分別用9 倍面積和36 倍面積的剛性板以 5m/s 的速度沖擊周期結構(見圖11).記錄剛性板在沖擊前后的速度變化,如圖12 所示. 圖11 周期結構分析模型Fig.11 Analytical models for periodic structure 圖12 單胞和周期結構在相同沖擊速度下的力學響應Fig.12 Mechanical responses of unit cell and periodic structures under the same impact velocities 結果顯示:在結構變形趨于穩定之后(T>1 s),相比于單胞結構,剛性板沖擊周期結構1(3×3 單胞排列)之后的速度誤差最大值為 15%,剛性板沖擊周期結構2(6×6 單胞排列)之后的速度誤差最大值為8%,這說明針對較大規模的周期結構,可以選取代表性單胞研究其力學性能. 具有單一幾何尺寸的單胞結構,其負剛度臨界載荷最大值為一確定量值,因此當沖擊載荷未達到該臨界載荷值時,結構將不能進入負剛度階段(圖1中的階段II),也即無法實現結構內部單元自主回彈耗能.因此,可以對結構進行梯度設計,以使其在不同沖擊載荷作用下,都能夠產生負剛度特性,從而提高結構在不同載荷環境下的能量損耗,實現更優的減振耗能[25]. 對于單一幾何尺寸的均勻單胞結構,設其在頂點受到外力f作用,由式(6),在已知無量綱化外載荷F時,可以得到F,其中h=Qt,I=bt3/12,則 由此可進行梯度結構設計,令部分曲梁胞壁厚度為t2,且t2=t/α,設 0<α<2,為常系數.在相同的Q,E,b值下,由式(6)可知,F是相同的,則所設計梯度單胞頂點所加外載荷為 圖13 表示DFcr隨 α 的變化關系,可知單胞負剛度臨界載荷最大值隨曲梁壁厚的變化十分明顯.故通過改變單胞結構中曲梁壁厚,可以得到具有多個負剛度臨界載荷最大值的單胞結構,由此可見,通過在結構中設計具有不同壁厚的曲梁單胞,構造梯度結構,以實現在同一結構中產生多種負剛度臨界載荷最大值,從而提高結構在不同沖擊載荷作用下的耗能效率. 圖13 梯度結構負剛度臨界載荷比值(DFcr)隨曲梁壁厚比值(α)的變化關系Fig.13 Variations of negative stiffness critical force ratio (DFcr) with the curved beam wall thickness ratio (α) for the gradient structure 由圖13 可知,梯度結構存在不同的負剛度臨界載荷最大值,在不同沖擊載荷下,其結構內部單胞都會出現自主回彈,實現能量的吸收;而均勻單胞結構的負剛度臨界載荷最大值單一,當外載荷作用小于該值時,不會出現結構的內部回彈調整,結構將無法實現對能量的吸收而只存在彈性應變能與動能之間的轉換.因此不同沖擊載荷作用下,梯度結構更具有吸能優勢和更好的環境適應性.此外,如果可以預設沖擊載荷可能的峰值,則可通過調整單胞結構的相關參數,如曲梁厚度、側壁厚度,頂點高度等,使負剛度臨界載荷最大值小于相應沖擊載荷峰值,從而獲得可調控的吸能效果.此外,在相同沖擊載荷作用下,通過對梯度結構梯度尺寸進行函數關系設計[26],使其吸能效果最優,亦是一個值得探討的方向. 為進一步比較梯度單胞結構與均勻單胞結構的吸能效果,本文利用ABAQUS 軟件模擬相同沖擊載荷下梯度單胞結構和均勻單胞結構的力學響應,有限元模型如圖14 所示,其中模型底部完全固定,采用C3D10M 實體單元,剛板施加了預定義速度場分別為 2m/s和 5m/s,沖擊梯度結構A和均勻結構B,并將剛性板上表面耦合到一參考點,輸出該點速度,通過監測沖擊載荷反彈后的速度來分析結構吸能的效率.其中針對梯度結構的梯度布置問題,主要通過改變曲梁胞壁的厚度t來實現梯度設計,如圖14所示,梯度結構A采用兩種不同單胞組成:在保持h=0.1 m,L=1 m不變的情況下,上部4 個單胞選取曲梁壁厚t(2)=0.01 m,下部兩個單胞選取曲梁壁厚t(1)=0.02 m,則根據形狀因子定義Q=h/t,可知Q(1)=5,Q(2)=10;均勻單胞結構B:Q=5,h=0.1 m,L=1 m,t=0.02 m. 圖14 兩種結構在不同沖擊速度下的屈曲模態Fig.14 Buckling modes of two structures under different impact velocities 在沖擊載荷作用下,兩種結構的力學響應如圖15 所示,在相同的沖擊速度v=2 m/s 下,沖擊梯度單胞結構A的剛板,在壓縮反彈過程中,其反彈速度小于沖擊均勻單胞結構B的剛板;且在沖擊過程中,梯度單胞結構A部分單胞已進入負剛度階段,而均勻單胞結構B所有單胞均仍處于正剛度階段,如圖14(a)所示,這是由于均勻單胞結構B只存在單一的負剛度臨界值點,必須在沖擊載荷達到單胞負剛度臨界載荷最大值時,結構才會進入負剛度階段.如圖16 所示,當沖擊載荷速度為 2m/s 時,均勻結構B中的單胞受到的沖擊載荷未能達到其負剛度臨界載荷最大值(Fmax1),結構內部將不會出現自我回彈調整;而梯度單胞結構A存在不同的負剛度臨界值點,在 2m/s 的沖擊載荷速度下,梯度單胞結構A部分單胞受到的載荷達到了其負剛度臨界載荷最大值Fmax2,進入負剛度階段,因而結構內部出現了自主回彈調整,從而提高了沖擊載荷作用下的能量吸收效能. 圖15 兩種結構在不同沖擊速度下的力學響應Fig.15 Mechanical responses of two structures under different impact velocities 圖16 梯度單胞結構A 與均勻單胞結構B 的力?位移曲線Fig.16 Force-displacement relations for gradient cell structure A and uniform cell structure B 當沖擊載荷速度增大到 5m/s 時,如圖15 所示,均勻單胞結構B在沖擊載荷作用后的反彈速度小于梯度單胞結構A;究其原因,雖然兩種結構的單胞均進入負剛度屈曲模態階段,如圖14(b)所示,但均勻單胞結構B的負剛度臨界載荷最大值較大(圖16),其滯回曲線所圍成的面積(圖16 虛線圍成的面積)大于梯度結構滯回曲線所圍成的面積(圖16 實線圍成的面積),因此耗能大于梯度結構,回彈速度更小. 觀察圖14,發現曲梁已與單元上下邊界發生接觸,因此需要考慮彈塑性變形以及接觸對本部分沖擊吸能的影響,但本文在有限元建模時采用的是彈性模型,這是因為負剛度結構實現循環(重復)加載的基礎即初彎曲梁的彈性變形.不同基底桿件所能承受的最大應力?應變不同,采用不同基底桿件時,結構有可能出現塑性變形,而本文為了實現完全回彈(不存在殘余變形),在選取基底材料時,首要保證結構的彈性變形;此外本文保持低速沖擊狀態(v≤5 m/s),結構會發生大變形,但塑性變形相比而言較小.因此這里忽略了彈塑性變形對沖擊吸能的影響.同時針對接觸問題,該負剛度結構在靜力加載過程中存在曲梁胞壁與基底桿件相接觸的現象,該接觸是結構設計時提前預設的,其主要目的是通過曲梁胞壁與基底桿件的接觸,阻止曲梁第二穩態(負剛度臨界載荷最小值Fmin<0)的出現,以實現負剛度結構的完全自主反彈. 同時,在沖擊載荷作用下,不同屈曲模態對應不同的單胞微結構構型,Bertoldi[27]指出,利用結構的不穩定性可以實現多孔結構的功能性設計,如負泊松比、吸能與彈性波傳播控制.基于結構不穩定性進行能帶調控可以實現濾波、導波、降噪等.本文所設計的三維吸能結構,在不同的屈曲模態下,具有不同的微結構構型,如圖14 所示,因此將呈現不同的能帶特性,必然具有與禁帶類似的濾波行為,作者前期針對多孔結構禁帶特性,進行了一系列的研究[28-29],因此如何表征隔離特性、以及同時利用禁帶與吸能,將是一項很有意義的研究.這也是作者后續的主要研究方向. 此外,在不同的載荷環境下,將上述獨立的單胞結構進行重組[30],可獲得更優的吸能效果.例如通過增加組成單胞單元組件個數(圖17),可提高結構穩定性,更好地實現結構內部回彈,防止結構出現非預設的屈曲模態變形及失穩;同時,充分利用了結構空間,利于實現低體積下的高耗能. 圖17 重組多單元負剛度結構Fig.17 Reassembled multi-element negative stiffness structure 利用結構多穩態特征進行多孔結構多功能設計,受到了廣泛的關注.然而多穩態結構無法實現自主反彈以及重復形變,限制了其工程應用.針對這一問題,本文通過單胞構型設計抑制其多穩態的出現,從而提出一種新型三維可回彈負剛度結構,采用理論解析和數值模擬對該結構的吸能特性進行了系統分析.分析結果表明:該新型負剛度結構具有較大的負剛度臨界載荷差值,因此在實現結構完全自主反彈以及重復利用的基礎上,獲得了更高的吸能效率.同時,為了適應復雜載荷環境,本文通過調整單胞幾何參數實現梯度結構設計,以獲得不同載荷狀態下不同的負剛度臨界載荷最大值,從而使得結構在不同載荷環境下,均能夠實現自主反彈,進而提高吸能效率,減小結構持續性的振動.本文的研究有望擺脫對外界沖擊條件的依賴,對工程結構的減振吸能應用具有重要的意義.3 吸能特性分析
3.1 單胞吸能效率分析
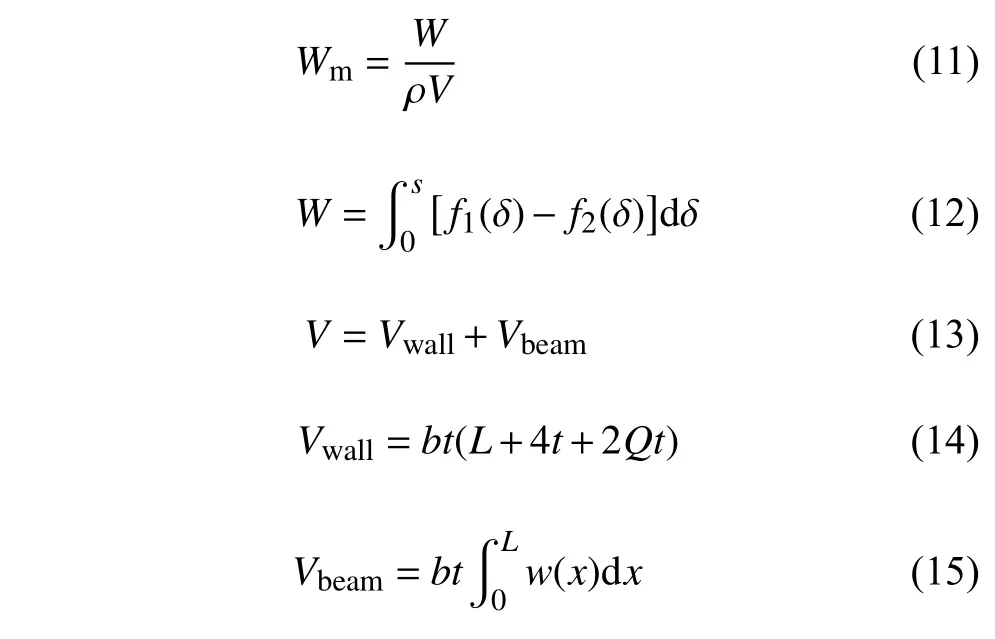
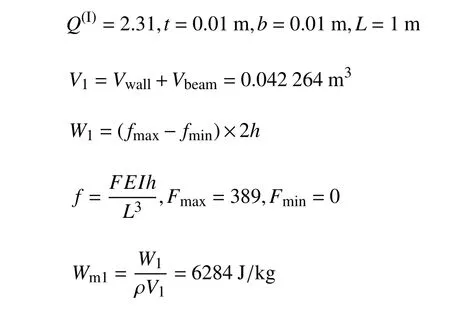
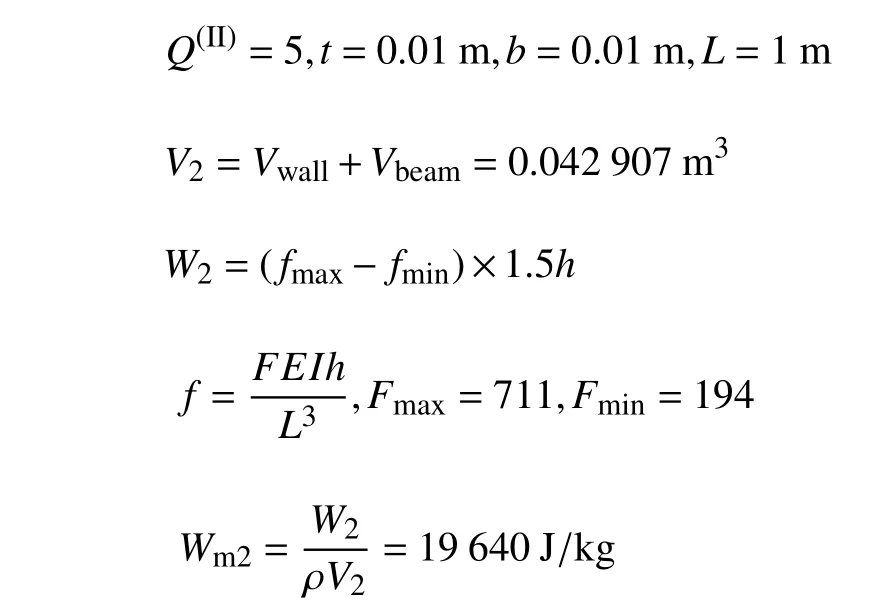


3.2 周期結構吸能效率分析


4 梯度結構吸能特性分析
4.1 梯度結構設計

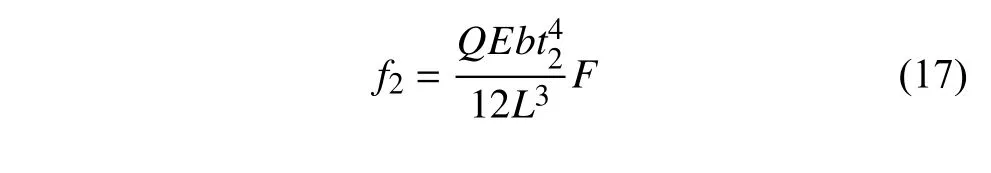
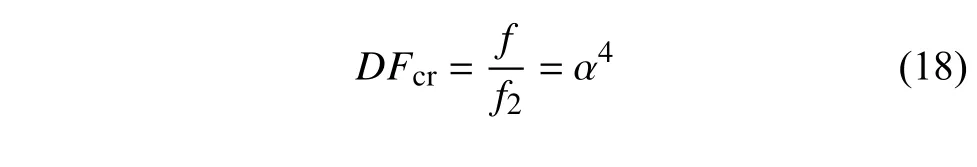

4.2 梯度結構吸能效率對比分析

5 討論

6 總結

