靈活轉(zhuǎn)化 巧解梯形
西北大學(xué)附屬中學(xué) 曹建聯(lián)
在初中數(shù)學(xué)教學(xué)過程中,不僅要教會(huì)學(xué)生熟記概念、套用公式、做對(duì)題目,而且要引導(dǎo)學(xué)生準(zhǔn)確理解數(shù)學(xué)概念,發(fā)展學(xué)生的數(shù)學(xué)思維,培養(yǎng)數(shù)學(xué)思想方法。在不同版本的初中數(shù)學(xué)教材中,多個(gè)章節(jié)內(nèi)容都滲透了最基本的數(shù)學(xué)思想方法,而轉(zhuǎn)化思想在數(shù)學(xué)學(xué)習(xí)過程中可以說是貫穿始終,每每學(xué)習(xí)新知識(shí)的時(shí)候,通常采用化未知為已知、化復(fù)雜為簡(jiǎn)單、化抽象為具體、化陌生為熟悉的思維方式。轉(zhuǎn)化思想會(huì)讓學(xué)生在探尋問題的相互聯(lián)系中,找到聯(lián)系的關(guān)鍵點(diǎn),獲得解決問題的突破口,鍛煉數(shù)學(xué)思維方式,提高學(xué)生的數(shù)學(xué)思維品質(zhì)。在初中數(shù)學(xué)教材的多個(gè)章節(jié)中,多處都應(yīng)用到了轉(zhuǎn)化思想,本文就著重探討轉(zhuǎn)化思想在解決梯形問題中的應(yīng)用。
作為特殊四邊形的梯形,是初中階段幾何部分學(xué)習(xí)的重要內(nèi)容,解決梯形問題對(duì)于學(xué)生來說既有似曾相識(shí)的感覺,又有無從下手的困惑,因此,在教學(xué)過程中,引導(dǎo)學(xué)生將梯形轉(zhuǎn)化為已經(jīng)學(xué)習(xí)過的三角形或平行四邊形就顯得尤為重要,通過轉(zhuǎn)化使問題得到簡(jiǎn)化,從而有利于學(xué)生解決問題。在教學(xué)中常用的轉(zhuǎn)化方式有以下四種情形。
【情形一】當(dāng)題目中出現(xiàn)底角的三角函數(shù)時(shí),則需構(gòu)造直角三角形,具體方法是通過作梯形的兩條高,將問題轉(zhuǎn)化為解直角三角形和矩形問題
例1:如圖1,梯形ADFE中,EF//AD,AE=DF,若AD=10,EF=4,tanA=2,求梯形的面積。
分析:由tanA=2 容易聯(lián)想到構(gòu)造含∠A的直角三角形,過點(diǎn)E作EB⊥AD,過點(diǎn)F作FC⊥AD,此時(shí)將梯形轉(zhuǎn)化為矩形和三角形,問題得到解決。
解題思路:
①證明四邊形EBCF為矩形,得到BC=EF=4;②證明△ABE≌△DCF,得到AB=CD=3;
③在Rt △ABE中,由tanA=2,AB=3,可得BE=6;④由梯形面積公式可得梯形的面積為52。
【情形二】當(dāng)題目中出現(xiàn)兩底角互余時(shí),則需將互余的兩個(gè)角轉(zhuǎn)化到一個(gè)三角形中,這時(shí)會(huì)形成一個(gè)直角三角形。
方法一:通過作一條腰的平行線,將互余的兩個(gè)角轉(zhuǎn)化到一個(gè)三角形中,利用直角三角形的相關(guān)知識(shí)使問題得以解決。
例2:如圖2,梯形ABCD中,AB//CD,∠A+∠B=90°,若AB=10,AD=4,DC=5,求梯形的面積。

圖2
分析:由條件∠A+∠B=90°會(huì)想到將∠A和∠B轉(zhuǎn)化到一個(gè)三角形中,因此,過點(diǎn)D作DE//BC,將梯形轉(zhuǎn)化為平行四邊形和直角三角形。
解題思路:
①由DE//BC得∠DEA=∠B,同時(shí)證得四邊形BCDE為平行四邊形,BE=CD=5,由AB=10 可得AE=5;
②由∠A+∠B=90°得△ADE為直角三角形,由AE=5,AD=4 得出DE=3 ,△ADE的面積為6;
③因?yàn)槠叫兴倪呅蜝CDE和△ADE等底同高,所以S四邊形BCDE=2S△ADE,則S四邊形BCDE=12;
④梯形的面積為6+12=18。
方法二:還可以通過將兩腰延長(zhǎng),構(gòu)造成直角三角形,使問題易于解決。
例3:如圖3,在梯形ABCD中,AB//CD,∠B=30°,∠A=60°,CD=AD=6,計(jì)算AB的長(zhǎng)度。
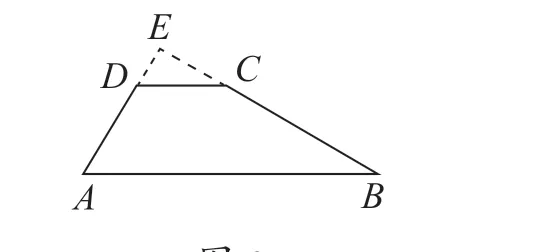
圖3
分析:由題目中的已知條件∠A=60°,∠B=30°,可以聯(lián)想到延長(zhǎng)AD和BC,將會(huì)使問題轉(zhuǎn)化為大家熟悉的直角三角形問題。當(dāng)然,該問題也可通過作兩條高解決。
解題思路:
①延長(zhǎng)AD和BC交于點(diǎn)E,由∠A=60°,∠B=30°可得∠E=90°;
②由已知條件AB//CD,可得到兩個(gè)含有30°的直角三角形,隨后問題即可迎刃而解。
【情形三】當(dāng)題目中的條件有對(duì)角線相互垂直時(shí),則需將直角轉(zhuǎn)化到對(duì)角線的一個(gè)端點(diǎn),具體方法是通過平移梯形的一條腰,容易計(jì)算三角形的面積,間接得到梯形面積。
例4: 如 圖4, 在 梯 形ABCD中,AD//BC,AB=CD, 對(duì) 角 線AC和BD相 互 垂 直, 若AD=4,BC=8,計(jì)算梯形ABCD的面積。

圖4
分析:由題目中所給條件AC⊥BD,可將AC平移到DE,過點(diǎn)D作DE與AC平行,且與BC的延長(zhǎng)線交于點(diǎn)E,得到△BDE為直角三角形,可通過計(jì)算三角形面積計(jì)算梯形面積。
解題思路:
①作DE//AC,由AC⊥BD得到DE⊥BD;
②又由AD//BC可證四邊形ADEC為平行四邊形,得DE=AC,CE=AD=4,由等腰梯形可知BD=AC,因此BD=DE,則△BDE為等腰直角三角形,BE=8+4=12;
③在等腰直角三角形BDE中,BE=12,S△BDE=36;
④由面積轉(zhuǎn)化可得梯形ABCD的面積為36。
【情形四】當(dāng)梯形為直角梯形時(shí),可以通過延長(zhǎng)兩腰,使圖形轉(zhuǎn)化為直角三角形,從而使問題得到解決,
例5:如圖5,在梯形ABCD中,AD//BC,∠B=90°,∠C=45°,AD=1,BC=5,E為AB的中點(diǎn),EF//DC交BC于F點(diǎn),求EF的長(zhǎng)。
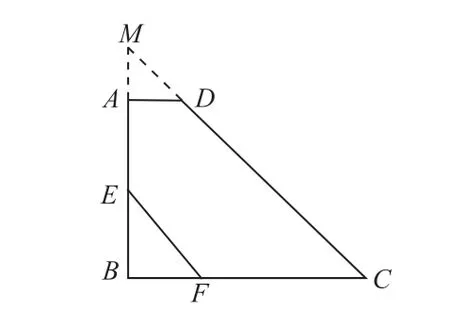
圖5
分析:由題目中的條件∠B=90°,∠C=45°,可延長(zhǎng)兩腰得到一個(gè)等腰直角三角形,將梯形問題轉(zhuǎn)化為熟知的等腰三角形問題。
解題思路:
①延長(zhǎng)BA和CD交于點(diǎn)M,由∠B=90°,∠C=45°可得△MBC為等腰直角三角形,即BM=BC=5;
②由AD//BC得∠ADM=∠C=45°,∠MAD=∠B=90°,則△MAD為等腰直角三角形,即AM=AD=1;
③由BM=4,AM=1,可得AB=4,因?yàn)镋為AB的中點(diǎn),所以BE=2;
④因?yàn)镋F//DC,所以∠BFE=∠C=45°,又因?yàn)椤螧=90°,所以△BEF為等腰直角三角形,從而可計(jì)算EF的長(zhǎng)度。
除了以上幾種常見的情形外,還有其他的輔助線添加方法,將梯形問題進(jìn)行轉(zhuǎn)化。
例6:如圖6,已知梯形ABCD中,AD//BC,EF是梯形中位線,△DEF的面積為4,則梯形ABCD的面積為多少?

圖6
分析:由EF為梯形的中位線可知點(diǎn)E為AB的中點(diǎn),可通過延長(zhǎng)DE構(gòu)造全等三角形,將梯形面積轉(zhuǎn)化為三角形面積,從而使問題得到解決。
解題思路:
①延長(zhǎng)DE和CB交于點(diǎn)M,因?yàn)锳D//BC,所以∠M=∠ADE, ∠MBE=∠A,又因?yàn)锽E=AE,所以△MBE≌△DAE,則梯形ABCD的面積等于△MCD的面積;
②因?yàn)椤鱉BE≌△DAE,所以DE=ME,則EF為△MCD的中位線,可得△DEF與△DMC相似;
③因?yàn)椤鱀EF的面積為4,所以△DMC的面積為16,所以梯形ABCD的面積為16。
總之,解決梯形問題的方法多種多樣,不止這幾種情形,在具體操作的過程中,根據(jù)題目所給已知條件,結(jié)合條件中邊、角、對(duì)角線的不同特點(diǎn),靈活應(yīng)用添加輔助線、圖形旋轉(zhuǎn)或割補(bǔ)的方法進(jìn)行圖形轉(zhuǎn)化,將梯形問題轉(zhuǎn)化為較為簡(jiǎn)單、熟悉且容易解決的三角形問題或平行四邊形問題,使問題分解、難度降低,從而達(dá)到解決問題的目的。當(dāng)然,復(fù)雜的梯形問題可能會(huì)綜合應(yīng)用多種添加輔助線的方法,但其本質(zhì)都是通過轉(zhuǎn)化的思想化繁為簡(jiǎn)、化未知為已知,靈活遷移所學(xué)知識(shí)和方法解決新問題,創(chuàng)新思維方式,提高學(xué)生的數(shù)學(xué)素養(yǎng)和創(chuàng)新能力。

