求解帶擾動的線性方程組的貪婪隨機Kaczmarz方法

巫文婷

（北京理工大學數學與統計學院，北京 100081）

對于系數矩陣為A∈Cm×n且右端向量為b∈Cm的大規模相容線性代數方程組

的求解，Kaczmarz方法［1］是經典的行處理迭代方法，在信號與圖像處理領域有著廣泛的應用。其每步迭代只需按照給定的循環順序選取系數矩陣的某一行，并將當前迭代向量正交投影至由該行所形成的超平面上。Strohmer等［2］提出按照與系數矩陣每一行的歐氏范數平方成比例的概率準則隨機選取系數矩陣的行，得到了收斂更為快速的隨機Kaczmarz方法。若用(·)*表示相應矩陣或向量的共軛轉置，則當初始迭代向量在A*的列空間中時，隨機Kaczmarz方法期望線性收斂［2-5］到線性代數方程組（1）的最小歐氏范數解x?=A?b，其中A?表示系數矩陣A的Moore-Penrose偽逆。當線性代數方程組（1）的右端向量發生擾動時，Needell［6］給出了隨機Kaczmarz方法的期望解誤差的上界，并說明了隨著迭代步數的增長，隨機Kaczmarz方法的期望解誤差會以線性速率下降至一個誤差閾值。之后，Zouzias等［7］對Needell所提出的期望解誤差的上界進行了改進。

影響隨機Kaczmarz方法收斂速率的關鍵在于其中所蘊含的用于選取每步迭代所需調用的系數矩陣行的概率準則。為了提高隨機Kaczmarz方法的收斂速率，Bai等［8-9］提出了一個可以獲取每步迭代中殘向量的模較大分量的概率準則，并基于該概率準則構造出了貪婪隨機Kaczmarz方法。當初始迭代向量在A*的列空間時，貪婪隨機Kaczmarz方法所產生的迭代序列收斂到線性代數方程組（1）的最小范數解x?=A?b且具有期望線性收斂速率

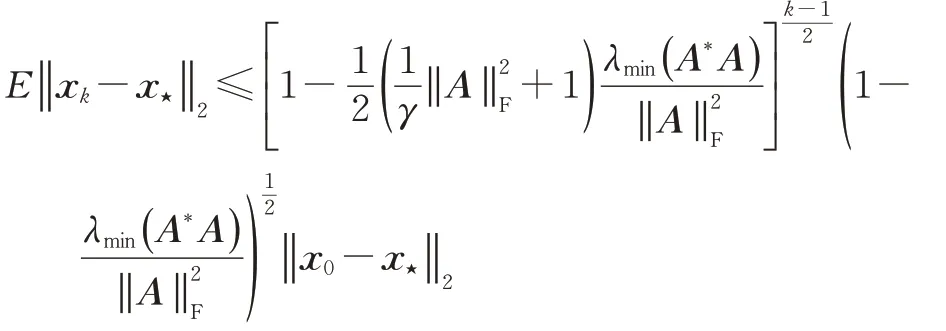
當線性代數方程組（1）的右端向量b被加上一個不為零的擾動向量r∈Cm時，實際求解的線性代數方程組問題將變為

其中，y=b+r。若對任意矩陣G∈Cm×n和任意向量u∈Cm，用G(i)和u(i)分別表示矩陣G的第i行和向量u的第i個分量，由于貪婪隨機Kaczmarz方法的第k步迭代將當前迭代向量x k投影至超平面=上，而線性代數方程組（1）的最小范數解x?=A?b滿足Ax?=y-r，故其并不能收斂到x?。在這種情況下，本文對貪婪隨機Kaczmarz方法的期望解誤差進行分析，得到了其上界，證明了隨著迭代步數的增長，由貪婪隨機Kaczmarz方法所產生的迭代解與原線性代數方程組（1）的最小范數解x?之間的誤差以線性速率下降至一個給定閾值。數值實驗表明本文所給出的閾值能夠很好地估計貪婪隨機Kaczmarz方法的迭代解誤差所能達到的最小值。

1 貪婪隨機Kaczmarz方法

不失一般性，在本文的討論中，總是假設系數矩陣A不存在零行，即A(i)≠0，i=1，2，…，m。當線性代數方程組（1）的右端向量發生擾動時，求解線性代數方程組（2）的貪婪隨機Kaczmarz方法［8］如下：

輸入：A，y，?與x0

輸出：x?

1：fork=0，1，…，?-1 do

2：計算

3： 確定正整數指標集

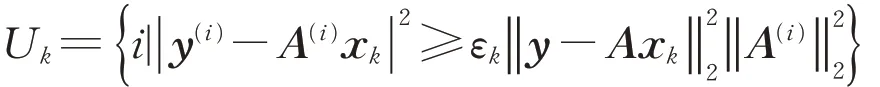
4： 計算向量r?k∈Cm的第i個分量

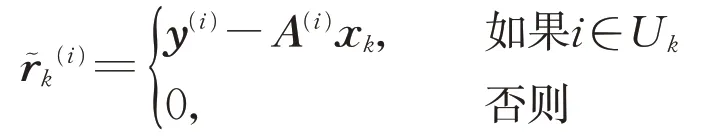
7：endfor

令R(A)和R(A)⊥分別為系數矩陣A的像空間和其像空間的正交補子空間，則有r=r R(A)+r R(A)⊥，其中r R(A)和r R(A)⊥分別表示向量r在R(A)和R(A)⊥上的正交投影。若線性代數方程組（1）右端向量的擾動r在系數矩陣A的像空間R(A)中，則線性代數方程組（2）等價于線性代數方程組

易知線性代數方程組（3）是相容的且其最小范數解為=A?(b+r R(A))。此時，若初始迭代向量在A*的列空間中，則求解線性代數方程組（2）的貪婪隨機Kaczmarz方法所產生的迭代序列期望線性收斂到x??。

2 誤差分析

與求解原線性代數方程組（1）的貪婪隨機Kaczmarz方法的分析［8］類似，根據求解線性代數方程組（2）的貪婪隨機Kaczmarz方法中εk的定義可知，對于k=1，2，…，由于

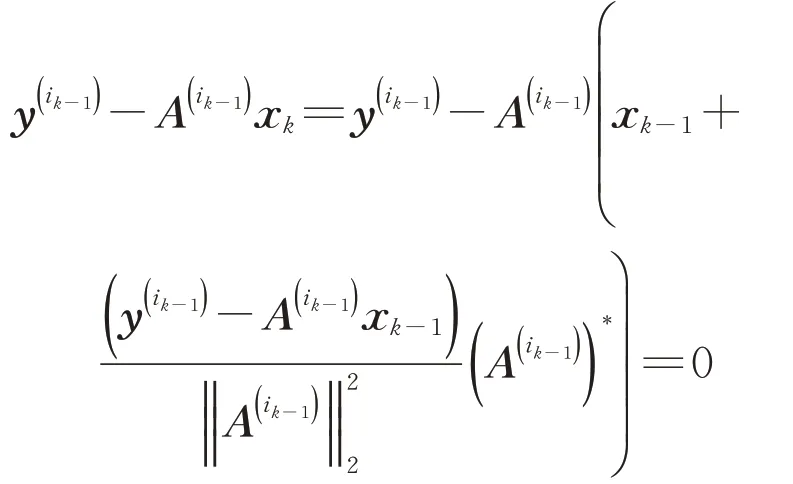
有

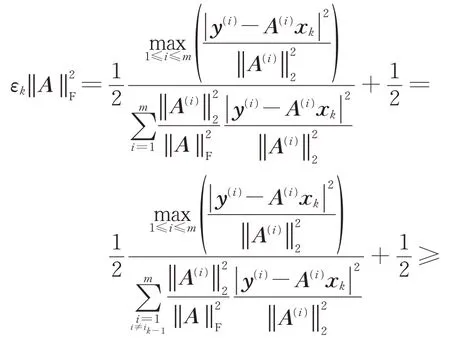
而對于k=0，有

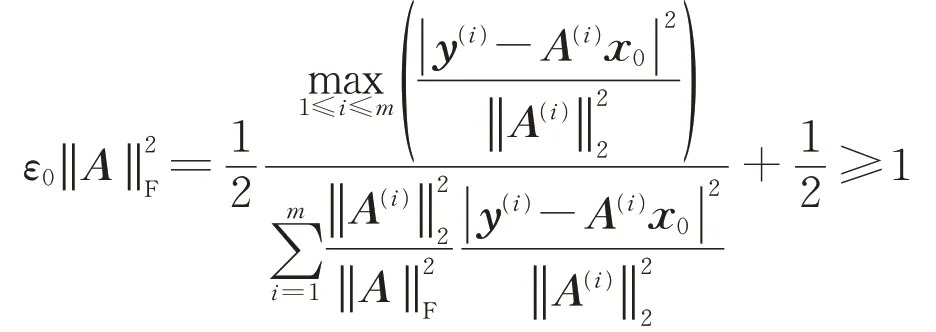
因此，可得引理1。

引理1求解系數矩陣為A∈Cm×n且右端向量為y∈Cm的線性代數方程組（2）的貪婪隨機Kaczmarz方法的概率準則中的量εk，k=0，1，2，…，滿足

和

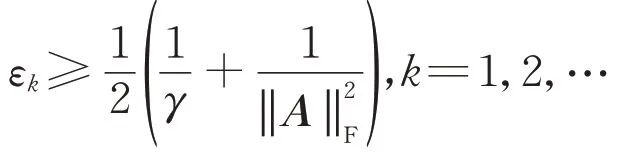
當線性代數方程組（1）右端向量的擾動r在R(A)中時，若初始迭代向量在A*的列空間中，則求解線性代數方程組（2）的貪婪隨機Kaczmarz方法所產生的迭代向量期望線性收斂到線性代數方程組（3）的最小范數解x??。對于一般的擾動情形，求解線性代數方程組（2）的貪婪隨機Kaczmarz方法所產生的迭代向量與x??之間的期望誤差的上界可以由引理2給出。

引理2如果初始迭代向量x0∈Cn在A*的列空間中，則貪婪隨機Kaczmarz方法求解擾動后的線性代數方程組（2）所產生的迭代序列與線性代數方程組（3）的最小范數解之間的期望誤差滿足

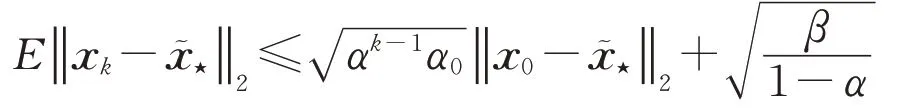
其中

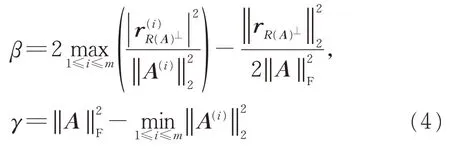
證明：由求解線性代數方程組（2）的貪婪隨機Kaczmarz方法的定義和Ax??=b+r R(A)可知

其中I表示具有合適階數的單位矩陣，則有

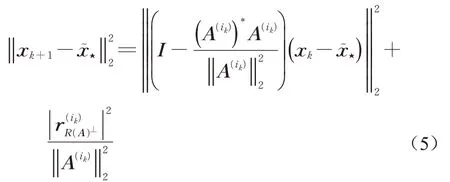
用Ek表示固定前k步迭代的條件期望，即Ek[·]=E[·|i0，i1，…，ik-1]，其中il(l=0，1，…，k-1)為第l步迭代所選取的行指標，則對等式（5）兩邊取條件期望可得

由于

可知

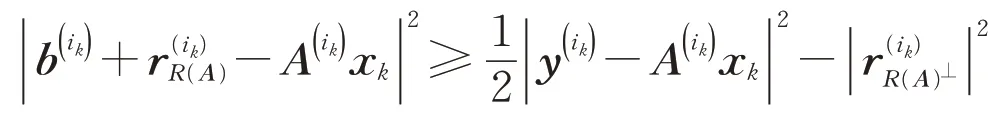
則根據正整數指標集Uk的定義可得

對于在矩陣A*的像空間R(A*)中的任意向量u，有不等式

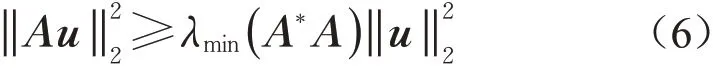
成立。利用該不等式，通過引理1、向量b+r R(A)-Ax k=A(-x k)∈R(A)和向量r R(A)⊥的正交性、x k-∈R(A*)以 及可 知，對 于k=1，2，…，有

而對于k=0，有

對不等式兩邊取期望可得對于k=1，2，…，有

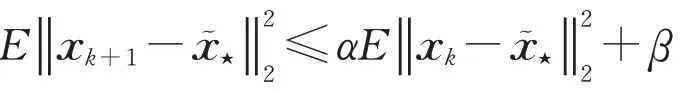
而對于k=0，有

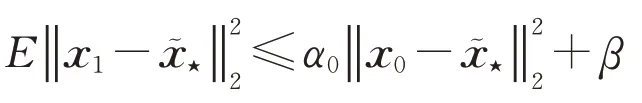
因此，由于0＜α＜1，β≥0，對于k=1，2，…，有

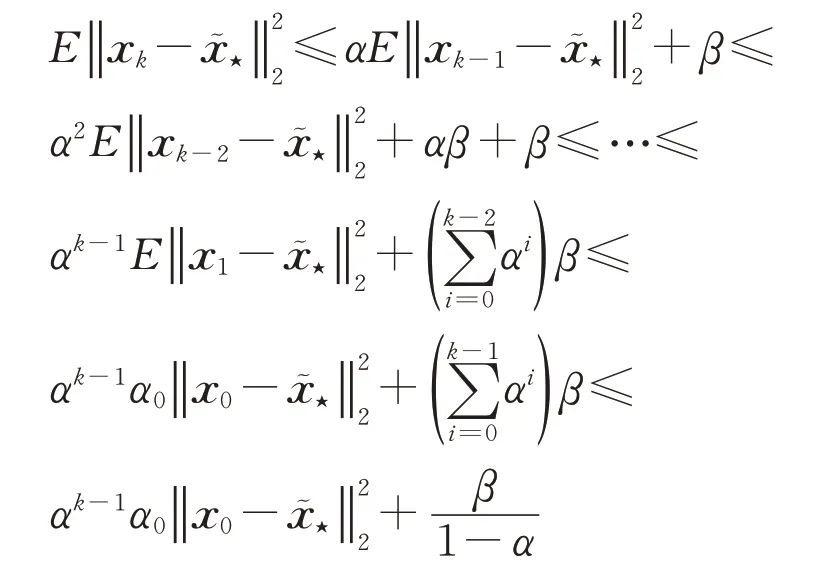
由Jensen不等式可知

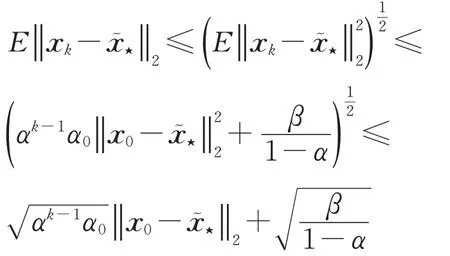
基于引理2，關于求解擾動后的線性代數方程組（2）的貪婪隨機Kaczmarz方法所產生的迭代近似解與原線性代數方程組（1）的最小范數解x?之間的期望誤差的上界，可以給出如下定理。

定理1如果初始迭代向量x0∈Cn在A*的列空間中且為線性代數方程組（3）的最小范數解，則貪婪隨機Kaczmarz方法求解擾動后的線性代數方程組（2）所產生的迭代序列與原線性代數方程組（1）的最小范數解x?=A?b之間的期望誤差滿足

其中，α、α0和β如（4）式中定義。

證明：因為-x?∈R(A*)，則通過不等式（6）可知

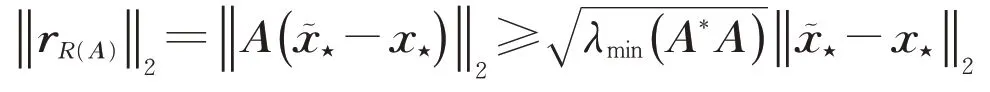
又因為有

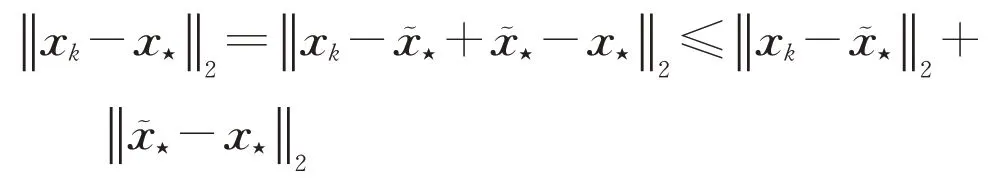
成立，則由引理2可得

定理1說明了當迭代步數k趨于無窮時，貪婪隨機Kaczmarz方法求解擾動后的線性代數方程組（2）所產生的迭代序列的期望相對解誤差以的線性速率下降至某個閾值，并給出了該閾值的估計

若r R(A)⊥為零，則擾動后的線性代數方程組（2）即為相容的線性代數方程組（3）。因此，求解線性代數方程組（2）的貪婪隨機Kaczmarz方法的迭代序列收斂到線性代數方程組（3）的最小范數解，且其與原線性代數方程組（1）的最小范數解x?的差趨于-x?。此時，如果初始迭代向量在A*的列空間中，則求解線性代數方程組（2）的貪婪隨機Kaczmarz方法所產生的迭代序列滿足

若r R(A)為零，則線性代數方程組（3）即為線性代數方程組（1），且線性代數方程組（3）的最小范數解即為x?=A?b。此時，如果初始迭代向量在A*的列空間中，則求解線性代數方程組（2）的貪婪隨機Kaczmarz方法所產生的迭代序列滿足

3 數值實驗

通過數值實驗測試貪婪隨機Kaczmarz方法求解帶右端項擾動的線性代數方程組（2）時的數值表現，并將所估計的閾值與貪婪隨機Kaczmarz方法所產生的真實迭代解誤差進行比較。

所測試的系數矩陣A分為兩類：一類為利用MATLAB函數randn隨機產生的元素服從標準正態分布的矩陣，矩陣維數分別為200×100 000和100000×200；另一類為取自稀疏矩陣庫［10］的稀疏矩陣bibd_16_8和ash958，矩陣維數分別為120×12870和958×292。

線性代數方程組（1）的右端向量b取為Ax*，其中x*∈Rn是利用MATLAB函數randn隨機產生的。線性代數方程組（1）的右端項的擾動向量r分為三類：一類為隨機擾動，一類為在系數矩陣的像空間中的擾動，另一類為在系數矩陣的像空間的正交補空間中的擾動。這三類擾動均由MATLAB函數randn生成，并且其歐氏范數為原始右端向量b的歐氏范數的0.0005倍。由于200×100000的隨機矩陣和稀疏矩陣bibd_16_8為行滿秩矩陣，故其所對應的右端項擾動r一定在其像空間中。所有計算均從初始向量x0=0開始。

圖1描繪了當線性代數方程組（1）的系數矩陣為隨機產生的矩陣且右端項擾動r為隨機擾動時，貪婪隨機Kaczmarz方法重復運行50次所產生的相對解誤差ERS的中值和閾值τ分別取以10為底的對數之后相對于迭代步數的曲線，其中

從圖1可以看出，貪婪隨機Kaczmarz方法所產生的相對解誤差下降至10-3左右之后不再減小，且閾值τ能夠很好地給出該最小值的估計。特別地，當系數矩陣為200×100 000的隨機矩陣時，τ與真實相對解誤差所能達到的最小值非常接近。

圖1 當m=200，n=100 000和m=100 000，n=200時，lg E RS和lgτ相對于迭代步數的曲線Fig.1 Pictures of lg E RS and lgτversus the iteration step when m=200,n=100000 and m=100000,n=200

圖2描繪了對于100 000×200的隨機產生的系數矩陣，當線性代數方程組（1）的右端項擾動r分別在系數矩陣的像空間和系數矩陣的像空間的正交補空間中時，貪婪隨機Kaczmarz方法重復運行50次所產生的相對解誤差的中值和閾值τ分別取以10為底的對數之后相對于迭代步數的曲線。從圖2可以看出，貪婪隨機Kaczmarz方法所產生的相對解誤差下降至10-3左右之后不再減小，且閾值τ能夠很好地給出該最小值的估計，特別當擾動向量r在系數矩陣的像空間中時。

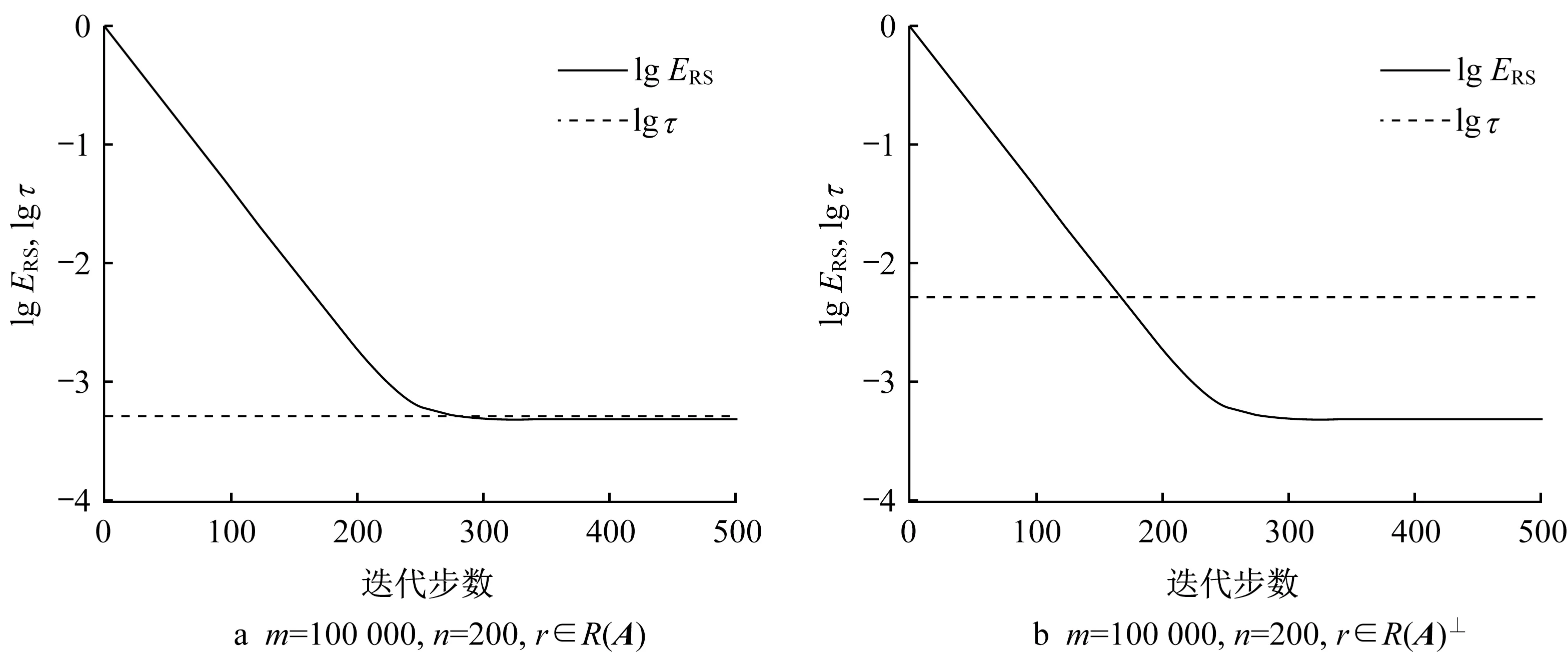
圖2 當m=100 000，n=200且r∈R(A)和r∈R(A)⊥時，lg E RS和lgτ相對于迭代步數的曲線Fig.2 Pictures of lg E RS and lgτversus the iteration step when m=100 000，n=200,and r∈R(A)and r∈R(A)⊥

當線性代數方程組（1）的系數矩陣為稀疏矩陣bibd_16_8和ash958時，圖3描繪了右端項擾動r為隨機擾動時，貪婪隨機Kaczmarz方法重復運行50次所產生的相對解誤差的中值和閾值τ分別取以10為底的對數之后相對于迭代步數的曲線；圖4描繪了右端項擾動r分別在系數矩陣的像空間和系數矩陣的像空間的正交補空間中時的相應曲線。類似地，從圖3和圖4可以看出，貪婪隨機Kaczmarz方法所產生的相對解誤差下降至10-3左右之后不再減小，且閾值τ能夠很好地給出該最小值的估計，特別當系數矩陣為bibd_16_8和當系數矩陣為ash958且擾動向量r在系數矩陣的像空間中時。

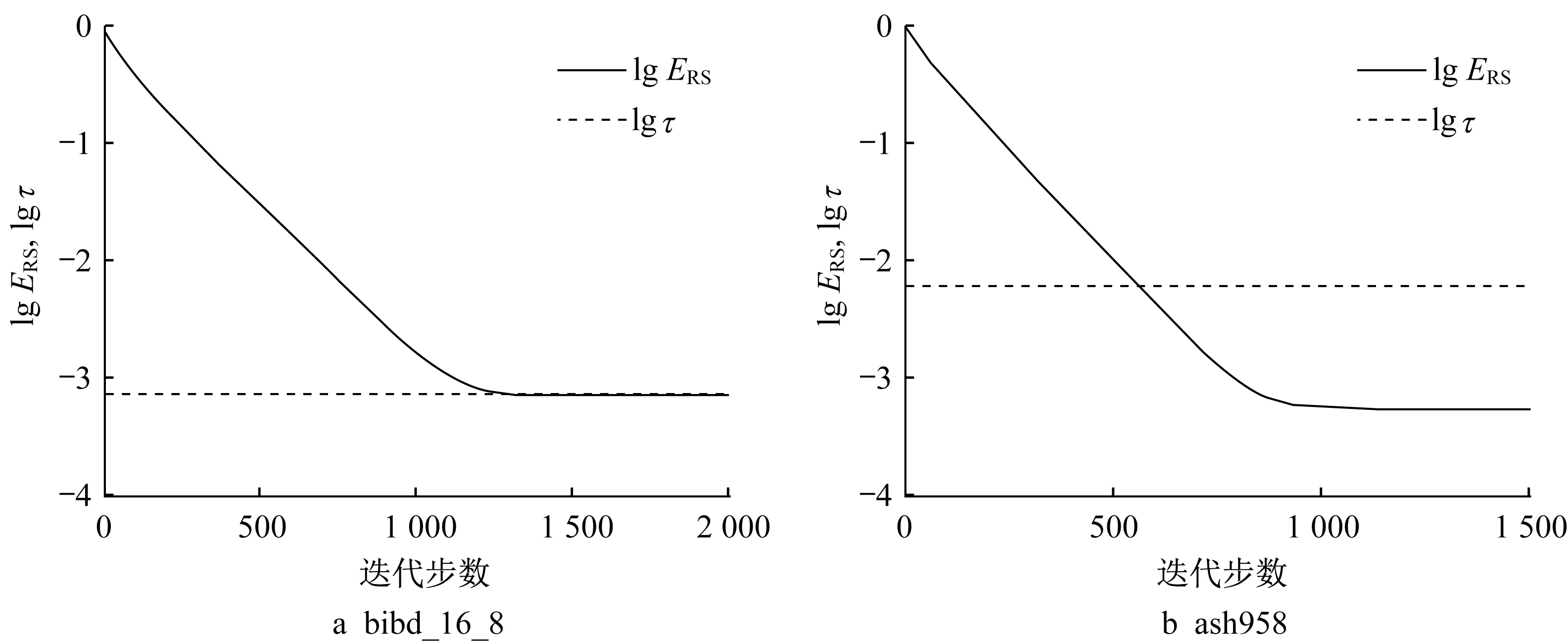
圖3 當矩陣為bibd_16_8和ash958時，lg E RS和lgτ相對于迭代步數的曲線Fig.3 Pictures of lg E RS and lgτversus the iteration step when the matrices are bibd_16_8 and ash958

圖4 當矩陣為ash958且r∈R(A)和r∈R(A)⊥時，lg E RS與lgτ相對于迭代步數的曲線Fig.4 Pictures of lg E RS and lgτversus the iteration step when the matrix is ash958,and r∈R(A)and r∈R(A)⊥

4 結論

當線性代數方程組的右端向量發生擾動時，證明了貪婪隨機Kaczmarz方法的期望解誤差以線性速率下降至一個給定閾值。數值實驗表明該閾值能夠很好地估計貪婪隨機Kaczmarz方法的迭代解誤差所能達到的最小值。可以發現當擾動不是很大且對解的精度要求不是很高時，貪婪隨機Kaczmarz方法仍然能夠很好地給出原線性代數方程組最小范數解的近似。