SO（3）上航天器自適應反步姿態跟蹤控制

史忠軍，邵長寶，張劍橋，趙艷彬

（1.上海航天技術研究院，上海 201109；2.上海衛星工程研究所，上海 201109；3.上海航天技術研究院 北京研發中心，北京 100081）

0 引言

航天器姿態控制是實現編隊飛行、交會對接、衛星通信、高分辨率對地觀測等任務的關鍵技術［1-4］。對于在軌運行航天器，受惡劣太空環境以及燃料消耗等因素影響，在進行航天器控制器設計時，往往需要解決轉動慣量不確定性以及外部干擾等問題。此外，航天器姿態動力學的非線性特性為高精度姿態控制的實現增加了難度。因此，近年來有大量學者在考慮航天器存在轉動慣量不確定性以及外部干擾情況下，采用非線性控制理論進行控制器設計，解決航天器姿態控制問題。

文獻［2，5］利用反步控制理論，解決了服務航天器與非合作航天器構成的組合體航天器的姿態穩定控制問題。LIU 等［6］通過設計H∞控制器解決了柔性航天器姿態穩定控制和振動抑制問題。XIAO 等［7］利用滑模控制理論設計控制器，解決了航天器姿態跟蹤和執行機構容錯控制問題。其中，反步控制方法因具有針對控制器設計、對干擾的魯棒性高等特點，在航天器控制領域被廣泛應用［8］。需要指出的是，在上述文獻中航天器的姿態或采用局部坐標表示，或利用四元數和修正羅德里格參數（Modified Rodriguez Parameters，MRPs）進行描述。然而，采用局部坐標或修正羅德里格參數描述航天器姿態運動時存在奇異問題，四元數則需要考慮退繞問題［1］。

由于方向余弦矩陣可以在SO（3）上全局無奇異地描述剛體姿態，因此文獻［9-10］基于方向余弦矩陣描述航天器姿態來建立動力學模型，解決了姿態跟蹤控制問題。但是，由于SO（3）的非線性特性，在SO（3）上直接進行控制器設計比較困難［11］。文獻［11-13］通過定義一個非負定的勢函數描述姿態跟蹤誤差，將姿態動力學修改為易于進行控制器設計的形式，解決了剛體的姿態跟蹤控制問題，但設計的傳統的比例-微分（PD）控制器對干擾的魯棒性差，且響應速度慢，控制精度低。ZHANG 等［1］基于此建模和控制器設計思想，采用滑模控制理論解決了航天器姿態跟蹤控制問題，但卻沒有考慮模型不確定性和外部干擾。

基于上述國內外研究現狀介紹與分析，本文針對存在模型不確定性和外部干擾的剛體航天器姿態跟蹤控制問題展開研究。首先，在系統存在模型不確定性和外部干擾情況下，通過定義姿態誤差勢函數，推導建立SO（3）上航天器相對姿態動力學模型；然后，設計自適應反步控制器對模型進行控制，并對系統的穩定性進行嚴格的數學證明；最后，通過數值仿真驗證所提出的控制算法的有效性。

1 姿態動力學描述

本文研究全驅動剛性航天器的姿態跟蹤控制問題。首先，為描述航天器的姿態運動，定義航天器本體坐標系Fb和地球慣性坐標系FI。FI的原點為地球質心，oxI沿著黃赤交線指向春分點，ozI軸與地球自轉軸重合，oyI軸通過右手定則確定；Fb的原點為航天器質心，oxb、oyb、ozb三個坐標軸與航天器的三個慣性主軸重合。航天器的姿態記為Fb到FI的轉動矩陣C∈SO(3)。SO（3）為由特殊正交矩陣構成的Lie 群，滿 足：SO(3)={C∈R3×3：CTC=I3×3，det(C)=1}，其中，R為實數集合；()T為矩陣的轉置；I3×3為3×3 的單位矩陣；det()為計算一個矩陣的行列式。用方向余弦矩陣描述的航天器姿態運動學和動力學方程為［1］

式中：ω=[ω1，ω2，ω3]T∈R3×1為本體系下航天器本體坐標系相對于慣性坐標系的姿態角速度；J∈R3×3為航天器轉動慣量；uc∈R3×1為航天器執行機構產生的控制力矩；d∈R3×1為航天器所受的外部干擾力矩。

()×：R3×1→?o(3)為計算 任意一 個三維向量x=[x1，x2，x3]T∈R3×1的反對稱矩陣，具體形式為

式中：?o(3)={A∈R3×3|AT=-A}為SO（3）的李代數。

記航天器的目標姿態為Cd，且滿足，其中，ωd∈C1∩L∞為航天器的目標角速度，則可以得到航天器的姿態跟蹤誤差和角速度跟蹤誤差為

對Ce和?求導，并將式（1）代入，可以得到航天器的姿態誤差運動學和動力學方程為

為解決航天器姿態跟蹤控制問題，需要設計控制器uc，使得ω?=0，Ce=I3×3。然而，SO（3）是一個具有9 個元素和6 個約束的非線性微分流形，姿態誤差運動學中Ce的存在導致在SO（3）上直接進行控制器設計比較困難［12］。一種常用的處理方式是通過定義一個非負定的誤差勢函數，將Ce轉化為一個三維姿態誤差向量，然后對姿態誤差運動學方程進行修改，再基于修正后的模型進行控制器設計。本文選用文獻［13］中定義的姿態誤差函數：

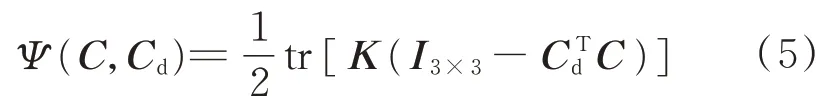
式中：K=diag(k1，k2，k3)＞0為正定對角矩陣；tr()為求矩陣的跡；姿態誤差函數Ψ(C，Cd)關于C=Cd局部正定，當C=Cd時，Ψ(C，Cd)=0［13］。

對Ψ(C，Cd)取導數，有

利用下述關系［14］

可以得到

對ec求導，可以得到修正后的姿態誤差運動學方程為

則航天器姿態跟蹤控制問題的動力學模型可以用式（4）和式（9）來描述。

此外，由于燃料消耗或釋放載荷等因素影響，在軌運行航天器的質量和轉動慣量無法精確獲得。因此，需要考慮航天器轉動慣量的不確定性。記航天器的實際轉動慣量為

式中：J0為轉動慣量的標稱部分；ΔJ為轉動慣量的不確定部分。

則考慮轉動慣量不確定性后，姿態誤差動力學方程改寫為

本文研究的姿態跟蹤控制問題，可以由式（10）和式（11）來進行描述。控制目標：考慮外部干擾和轉動慣量不確定性，在?滿足上述假設情況下，設計自適應控制器uc，使得姿態跟蹤誤差ec可以一致漸近收斂到零點附近的小鄰域內。

2 自適應反步控制器設計

本章將通過設計自適應反步控制器來處理由外部干擾和轉動慣量不確定性產生的系統總干擾，并實現控制目標。

步驟1定義下面的反步控制虛擬變量：

式中：α為虛擬控制輸入。

將式（11）、式（12）和式（13）聯立，可以得到構造的虛擬變量z1的動力學方程為

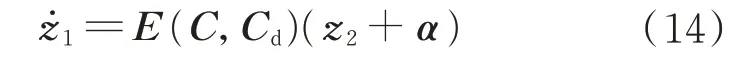
然后，選取Lyapunov 函數：

對V1求導，并將式（14）代入，可得

設計虛擬控制α為

式中：K1＞0為控制器設計參數。

將式（17）代入式（16），有

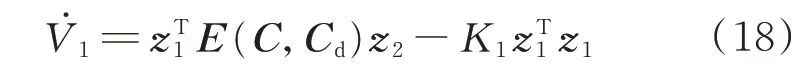
步驟2對式（13）取導數，并將式（11）代入，可以得到構造的虛擬變量z2的動力學方程為

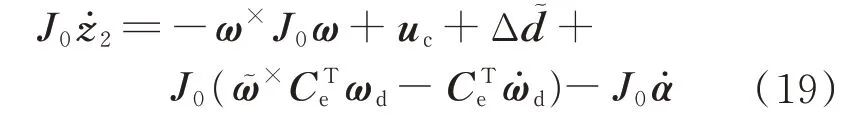
然后，選取Lyapunov 函數

式中：γ1＞0為待設計參數為系統總干擾的估計誤差為干擾的估計值。

對V2取導數，得

步驟3設計如下的自適應反步控制器：

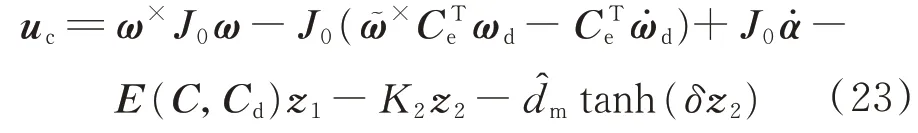
式中：K2＞0、δ＞0為控制器設計參數。

將式（23）代入式（22），得到

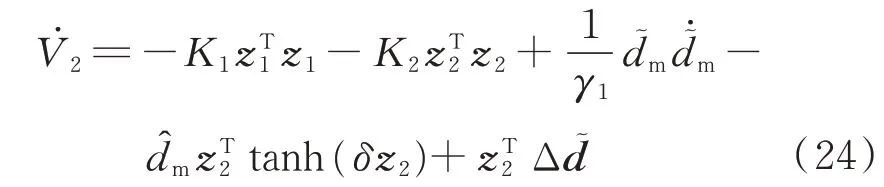
為了估計系統的總干擾dm，設計如下的自適應控制率：

式中：γ2＞0為控制器設計參數。

將式（25）代入式（24），得到

3 控制系統穩定性分析

為了后續穩定性證明需要，首先給出下面引理。

引理1對于雙曲正切函數滿足下述不等式［15］：

結合步驟1～3，本文研究結果可以用下述定理進行概括。

定理1考慮由式（9）和式（11）描述的航天器姿態跟蹤控制系統，在滿足系統所受總干擾有界假設條件下，應用控制律式（23）和自適應律式（25），航天器姿態跟蹤誤差ec能夠一致漸近收斂到零點附近的小鄰域內。

證明選取式（21）的Lyapunov 函數，經過計算后可以得到式（26）。對于項來說，滿足

將式（28）代入式（26），并利用引理1，可以得到

注1：對于本文研究的航天器姿態跟蹤控制問題來說，最終的控制精度取決于，較小的γ2和較大的δ可以得到較小的χ。尤其是較大的δ可以明顯改善系統對于干擾的魯棒性。但同時需要注意，δ越大會導致tanh 函數越接近符號函數，會使系統產生抖振。因此，在進行控制器參數設計時，要在穩態精度和系統性能間做好平衡。

注 2：對于角速度跟蹤誤差來說，ω?=z2+α，由文獻［13］可知，E(C，Cd)有界。因此，根據z1、z2有界可知，角速度跟蹤誤差ω?也是一致最終有界的。

注3：受航天器姿態控制執行機構的動力學特性影響，在工程應用過程中，需要考慮執行機構的輸出飽和問題。因此，實際的控制輸出為

4 仿真試驗及結果分析

本章將通過數值仿真分析驗證本文所提出的控制方法，可以有效地解決航天器姿態跟蹤控制問題。仿真過程中航天器參數如下，轉動慣量標稱部分為

轉動慣量不確定部分為ΔJ=0.15J0，航天器的控制力矩上限為umax=0.5 N·m，航天器所受的外部干擾力矩為

初始時刻的航天器姿態信息為：姿態轉動矩陣C(t=0)=I3×3；姿態角 速度為ω(t=0)=[0.01-0.01-0.01]T×180/π((°)/s)；航天器的初始目標姿態為

為了驗證本文所提出的算法的有效性，主要考慮兩種情況的對比仿真。

情況1：本文所提出的自適應反步控制器式（23）、式（25），控制器參數設計為：K=diag ( [ 1 1 1 ] )；K1=10；K2=8；δ=100；γ1=0.002；γ2=0.001。

情況2：文獻［12］中的類PD 控制器，用來與本文所設計的控制器的控制效果進行對比，說明本文所提控制算法的優越性，控制器參數設計為：KΩ=2.5。

情況1 仿真結果如圖1～圖3 所示，仿真時間設置為150 s。圖1為航天器姿態跟蹤誤差，圖2為角速度跟蹤誤差。圖中可見，航天器姿態運動誤差在30 s內收斂到穩態，通過系統狀態收斂后的曲線放大圖可以看出，姿態控制精度為：|eci|＜2×10-3°，姿態角速度控制精度為：。相應的控制力矩變化曲線如圖3 所示。圖中可見，在整個仿真過程中控制力矩沒有超過航天器控制輸出上限，表明了本文所提控制方法具有一定的工程應用價值。

圖1 姿態跟蹤誤差（情況1）Fig.1 Attitude tracking errors（Case 1）

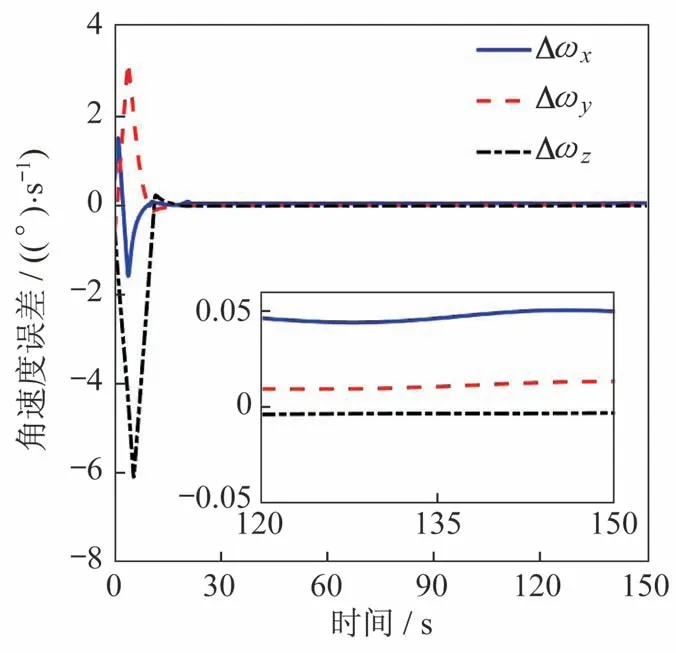
圖2 角速度跟蹤誤差（情況1）Fig.2 Angular velocity tracking errors（Case 1）

圖3 控制力矩（情況1）Fig.3 Control torques（Case 1）

情況2 仿真結果如圖4～圖6 所示，仿真時間設置為300 s。圖4為航天器姿態跟蹤誤差，圖5為角速度跟蹤誤差。圖中可見，航天器姿態運動誤差在150 s 左右收斂到穩態，通過系統狀態在120 s 到150 s，以及收斂后的曲線放大圖可以看出，與本文設計的控制器式（22）的仿真結果相比，無論是誤差收斂時間還是最后的穩態控制精度，本文所設計的控制器均優于文獻［12］。

圖4 姿態跟蹤誤差（情況2）Fig.4 Attitude tracking errors（Case 2）

圖5 角速度跟蹤誤差（情況2）Fig.5 Angular velocity tracking errors（Case 2）

圖6 控制力矩（情況2）Fig.6 Control torques（Case 2）

此外，對于在軌運行航天器來說，能量消耗是決定其在軌運行壽命的一個關鍵因素。為了進一步比較兩種情況的仿真結果，定義能量消耗函數為

式中：T=150 s。

兩種情況的能量消耗曲線如圖7 所示。圖中可見，與文獻［12］控制器相比，本文所設計的控制方法可以在保證較高的控制性能的同時，將能量消耗降低72%左右。通過上述兩種情況的仿真結果及對比分析可以發現，在系統存在外部干擾和模型不確定性情況下，本文所提出的控制方法可以有效地解決航天器姿態跟蹤控制問題，且與傳統的PD 控制器相比，可以實現更好的控制效果。

圖7 能量消耗Fig.7 Energy consumption

5 結束語

本文研究了剛體航天器姿態跟蹤控制問題，在姿態跟蹤系統存在模型不確定性和外部干擾情況下，推導了SO（3）上航天器相對姿態動力學模型。在模型中，采用方向余弦矩陣描述航天器姿態運動，且通過引入非負定的勢函數描述姿態跟蹤誤差，將動力學模型轉換成了易于控制器設計的形式，并有效避免了用其他姿態描述方式表示姿態時，引起的奇異或退繞問題。基于此模型，設計了自適應反步姿態控制器，保證了閉環控制系統的最終一致有界收斂，并通過Lyapunov 穩定性分析方法，證明了控制系統的收斂特性。最后，對所設計的控制算法進行了仿真校驗，且與文獻［12］中的PD 控制器進行了對比分析。結果表明，本文提出的控制方法收斂速度快、控制精度高、能量消耗低，具有一定的工程應用價值。此外，本文的研究對象為剛體航天器，而為了增加航天器的在軌功能，一般都配備有太陽電池陣、天線等柔性附件。柔性附件在軌會發生振動，且振動信息一般無法測量。因此，未來的一個研究方向是如何將本文設計的控制算法用于解決柔性航天器姿態控制問題。