車路協(xié)同環(huán)境下干線交叉口貨車車速引導模型研究

張 鵬，王扶春，李文權

(1.江蘇大學 汽車與交通工程學院，江蘇 鎮(zhèn)江 212013；2.東南大學 交通學院，南京 210096)

隨著經(jīng)濟的發(fā)展，貨運出行需求持續(xù)增長，貨運車輛向大型化、重載化方向發(fā)展。貨車面對交通信號變化時，需要更長的時間、距離來加減速，這就導致貨車停車再啟動通過交叉口會造成更多的交通延誤和空氣污染，并且停車再啟動對貨車本身使用壽命和路面車轍的產(chǎn)生都會有很大影響。相關研究表明，貨車停車再啟動通過交叉口油耗值比勻速直接通過時油耗值大2.0～4.0倍[1]。近些年，隨著車聯(lián)網(wǎng)技術突飛猛進的發(fā)展，車與車、車與路實現(xiàn)了信息交互和共享通信，多目標協(xié)同配合達到優(yōu)化利用系統(tǒng)資源、提高道路交通安全、緩解交通擁堵的目標[2]。因此，利用車聯(lián)網(wǎng)環(huán)境給予貨車車速引導，讓貨車直接通過信號交叉口而不是停車再啟動通過可以有效減少行程時間，減低燃油消耗，緩解交通延誤，減少闖紅燈行為，并鼓勵貨車行駛特定線路。

國內(nèi)外車速引導研究大部分集中在小汽車和公交車方面，針對貨車車速引導的研究和應用較少。現(xiàn)有針對公交車車速引導的研究中，馬萬經(jīng)等[3]提出了基于車路協(xié)同環(huán)境下保證公交行駛情況最優(yōu)，設計了交叉口信號控制模型和最佳車速調(diào)整的策略。張鵬等[4]考慮了公交運行車速可以引導調(diào)節(jié)的環(huán)境，建立公交多申請下公交車速引導和交叉口信號配時集成優(yōu)化的整數(shù)線性規(guī)劃模型。G.Abu-Lebdeh[5]通過結合公交車輛速度和信號配時，提出了一種整合最優(yōu)引導車速的動態(tài)交叉口信號配時算法模型，并通過仿真驗證了模型的可行性。KeVin N.Balke等[6]討論了在不破壞綠波帶的情況下為信號交叉口提供公交優(yōu)先控制的模型。上述針對公交車的車速引導模型研究中，引導模型中加減速時間為零，忽略了加減速過程，但是對于質量較大的貨車，其加速度小，加減速過程緩慢，不能忽略加減速時間。

現(xiàn)有針對小汽車車速引導的研究中，李鵬凱等[7]基于車路協(xié)同環(huán)境，建立信號交叉口單車車速引導模型，求解汽車的最優(yōu)行駛車速，并利用vissim仿真軟件對實地交叉口進行仿真驗證。Rakha H A等[8]通過計算通行時間來判斷汽車是否需要變速，對于需要進行加減速的情況進行優(yōu)化，以加減速時間為參數(shù)，以最小油耗為目標，建立交叉口車速引導模型。De Nunzio G等[9]通過剪枝算法設計最優(yōu)速度曲線模型，計算速度比以往更快。Barth M等[10]利用車路協(xié)同環(huán)境設計單車動態(tài)速度規(guī)劃模型來確保汽車不停車通行信號交叉口，并在仿真環(huán)境下驗證了模型的節(jié)能減排效果。Xiang X等[11]研究了基于閉環(huán)反饋的引入汽車滑動的車速引導模型，利用汽車慣性滑動來補償巡航，仿真驗證說明對汽車的燃油經(jīng)濟性存在幫助。針對小汽車的車速引導模型研究中，小汽車引導模型加速度限值往往只給出經(jīng)驗估值，而貨車變速器擋位傳動比跨度大，低擋位加速度限值遠超過高擋位的加速度限值，如果取低擋位加速度限值作為引導加速度經(jīng)驗估值，貨車將難以按照給定引導策略行駛；如果取高擋位加速度限值作為引導加速度經(jīng)驗估值，貨車難以發(fā)揮最大功率，加速和爬坡能力會受到很大限制。

綜上,對于貨車的車速引導模型的建立，有必要按各擋位加速度限值進行車速引導。為此，本文中結合換擋操作對貨車進行車速引導來調(diào)節(jié)貨車到達下一交叉口時刻，以總行程最短時建立車速引導模型。

1 模型構建

1.1 結合換擋操作的約束模型

為使研究問題明確化，設立以下假設：① 場景為車路協(xié)同環(huán)境，貨車與路側設備之間可隨時進行雙向通信；② 研究范圍為單一干線交叉口，交通流處于非飽和狀態(tài)，每個進口道交通流基于歷史平均；③ 研究對象為單輛貨車，不考慮車輛排隊跟馳等外部因素，假定貨車沿直線行駛；④ 假設貨車100%服從換擋操縱和車速引導方法。

1.1.1基于換擋策略的貨車加減速度限值

換擋操作采取最佳動力性換擋策略，同一油門開度下，若相鄰擋位的加速度與速度曲線有交點，則該交點為此相鄰擋位的升擋點；否則，取高擋位的最高車速作為升擋點[12]，得出貨車各擋位換擋車速vi，具體表達式如式(1)所示：

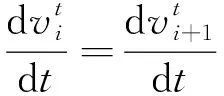
(1)

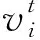
根據(jù)汽車動力學方程，車輛瞬時加速度a的表達式為：

(2)

式中：a為瞬時加速度，m/s2；Ttq為發(fā)動機輸出轉矩，N·m；ii為i擋時變速器傳動比；i0為主減速器傳動比；η為傳動系機械效率；r為車輪半徑，m；v為瞬時車速，km/h；f為滾動阻力系數(shù)；CD為空氣阻力系數(shù)；δ為旋轉質量換算系數(shù)；m為車重，kg；g為重力加速度，m/s2。

油門開度為100%時，求得換擋速度和各擋位能取得最大加速度限值。從式(2)可以看出，瞬時車速v越大，瞬時加速度a越小，為了保證換擋后車輛能持續(xù)取得各擋位給定加速度限值，規(guī)定各擋位加速度限值aimax以換入該擋的換擋速度vi代入式(2)求得。

車輛減速度限值與擋位操作關系較小，但貨車減速到換擋速度時也要換擋，因為車速下降而擋位不降會導致脫擋，甚至造成熄火。極限狀態(tài)下車輛60 km/h性能測試數(shù)據(jù)分析表明，制動時減速度限值通常小于-8.5 m/s2，但在實際駕駛過程中，駕駛員進行加減速操作時不會達到車輛的性能極限[13]。且駕駛員可以接受的最大減速度限值為-2.5～-1.5 m/s2[14]。因此，綜合考慮貨車性能與駕駛舒適度，設定貨車減速度限值admax為-1.5 m/s2。

1.1.2基于時空運動軌跡的約束條件

貨車車速引導策略：擋位總數(shù)為n的貨車到達車速引導區(qū)時，擋位應調(diào)至初速度v0所匹配的m(1≤m≤n,m∈N)擋，其有車速引導軌跡如圖1所示，時刻點對應時刻為貨車換擋時刻和進入勻速行駛時刻。車速引導模型會引導貨車從速度v0開始勻變速至最終車速vc后勻速通過交叉口，期間瞬時速度一旦達到換擋速度就進行換擋。換擋后加減速度限值發(fā)生改變，加減速度進行再次取值。隨著每個擋位加速行駛時間t1,t2,…,tn、勻速行駛時間tc和最終車速vc的改變，貨車的行駛軌跡會發(fā)生改變。

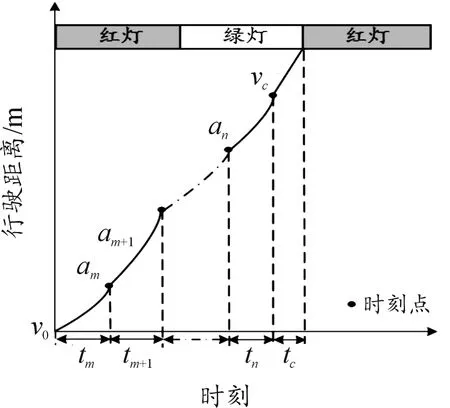
圖1 車速引導模型下貨車時空軌跡圖

交叉口信號燈配時策略：設定信號開始時刻為該相位紅燈開始時刻，即0時刻。

分析時空運動軌跡，需要滿足的約束有：

1) 時間約束：

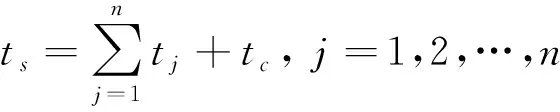
(3)

tj,tc≥0,j=1,2,…,n

(4)

sign(tk+1)≤sign(tk)

k=m,m+1,…,n-1

(5)

式中：ts為貨車在引導區(qū)行駛時間(s)；tj,tk,tk+1分別為j,k,k+1擋位行駛時間(s)；tc為勻速行駛時間(s)；sign()為符號函數(shù)，括號里的值為正數(shù)、0、負數(shù)時，分別取值為1、0、-1。建立式 (5) 的原因是避免貨車行駛過程中越級加擋。

(6)

式中：tt為停車時間(s)，為貨車到達停車線時刻與當前相位綠燈開始時刻差值，如果差值為負數(shù)，則值為0；C為信號周期(s)，默認信號周期開始時刻為0時刻；Gs為信號周期開始時，首次該相位綠燈開始時刻；dd為貨車到達引導區(qū)時刻；floor()為向下取整函數(shù)。

2) 速度約束：

(7)

式中：vc為最終車速(km/h)；aj為j擋位加速度取值(m/s2)。

(8)

式中：vm,vk,vk+1分別為m,k,k+1擋位換擋車速(km/h)；ak為k擋位加速度取值(m/s2)。建立式(8)用來保證貨車瞬時車速到達換擋車速時能立即換擋。

3) 加速度約束：

admax≤aj≤ajmax,j=1,2,…,n

(9)

式中：admax為減速度限值(m/s2)；ajmax為j擋位加速度限值(m/s2)。

4) 運動學約束：

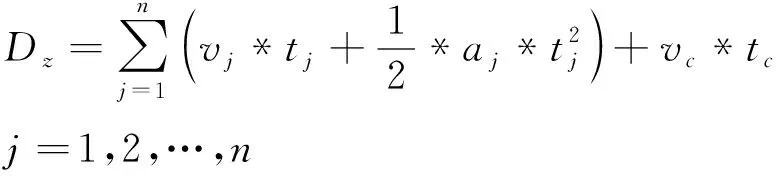
(10)

式中：Dz為引導區(qū)距離(m)。

1.2 基于最短行程時間的目標函數(shù)

研究內(nèi)容是生成以最短行程時間為目標的最優(yōu)軌跡曲線，行程總時間由行駛時間、停車怠速時間和停車再啟動時間3部分組成。為方便計算，其中行駛時間為貨車勻變速和勻速行駛總時間ts、停車怠速時間為停車時間tt、停車再啟動時間tq*sign(tt)，tq簡化為車輛從靜止加速至道路平均車速的時間，為定值。因此車速引導模型的目標函數(shù)為

Tz=ts+tt+tq*sign(tt)

(11)

式中：Tz為行程總時間(s)；tq*sign(tt)為貨車停車再啟動時間；tq為定值，當停車時間tt為0時，貨車再啟動時間為0。

綜上，最終數(shù)學模型為

(12)

1.3 模型求解

目標函數(shù)和約束函數(shù)都為線性函數(shù)，貨車換擋車速vi、擋位加速度限值ak、貨車進入引導區(qū)時刻dd和初速度v0、信號周期C、相位綠燈與紅燈時長都為已知條件；擋位行駛時間tj、勻速行駛時間tc和最終車速vc為自變量，其余參數(shù)均可通過自變量表達，利用Matlab進行線性規(guī)劃求解。

2 算例分析

使用Matlab軟件對貨車車速引導優(yōu)化模型進行算例測試，通過算例結果驗證模型的整體功能和效果。為使測試具有針對性，對測試的車輛、場景以及方案做出設定。

2.1 算例參數(shù)設置

在貨車車速引導算例中，引導距離設為1 000 m；預設交叉口信號控制為固定配時，根據(jù)我國現(xiàn)行的交通法規(guī)，黃燈時車輛禁止通過停止線，為便于研究，將黃燈亮起時視為禁止通行，信號周期C=130 s，紅燈時長70 s，綠燈時長60 s，周期開始時刻為相位紅燈開始時刻，為0時刻，Gs=70。

現(xiàn)選取5擋貨車JN162作為測試主體，其質量取值為17 000 kg，該型號貨車求得的各擋換擋速度和加速度限值如表1所示。道路最高限速取60 km/h，道路不設最低限速，道路平均車速為50 km/h，tq經(jīng)簡單計算求得值為26.3 s。

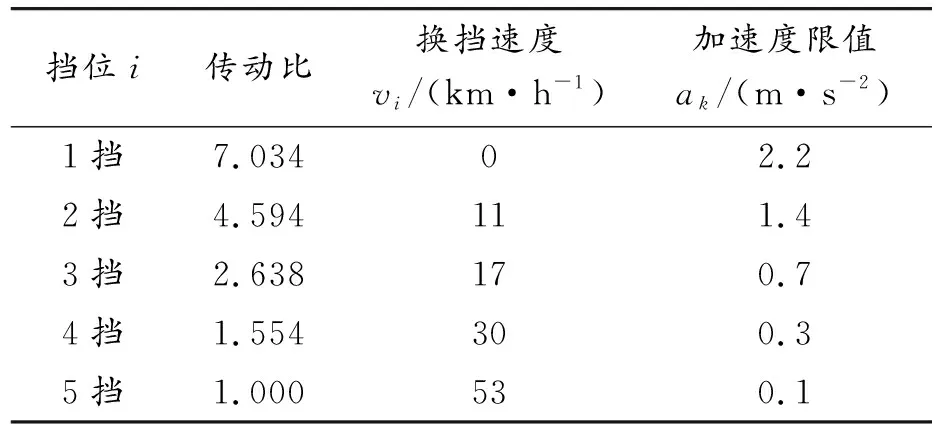
表1 貨車JN162最佳動力性換擋速度和各擋加速度限值

算例測試中調(diào)整貨車進入車速引導區(qū)的初速度v0和到達時刻dd，使貨車在不同擋位下以初速度v0行駛至交叉口出現(xiàn)停車再啟動與直接通過2種情況，共計10種情形。同時對各情形在無車速引導策略下進行1次測試，將行程時間和停車時間作為對照。沒有車速引導策略下的貨車將保持勻速行駛至停車線。各測試場景的輸入?yún)?shù)見表2。

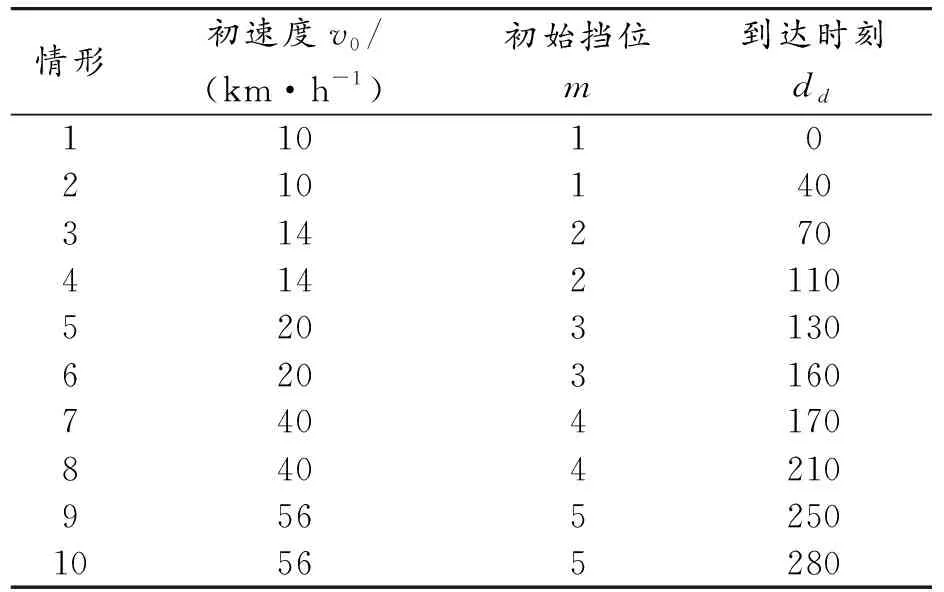
表2 算例測試場景參數(shù)輸入

2.2 算例測試結果分析

圖2、3分別是有無車速引導情況下，貨車在信號交叉口車速引導區(qū)域通行過程中的時空軌跡圖，時刻點對應時刻為貨車換擋時刻和進入勻速行駛時刻。

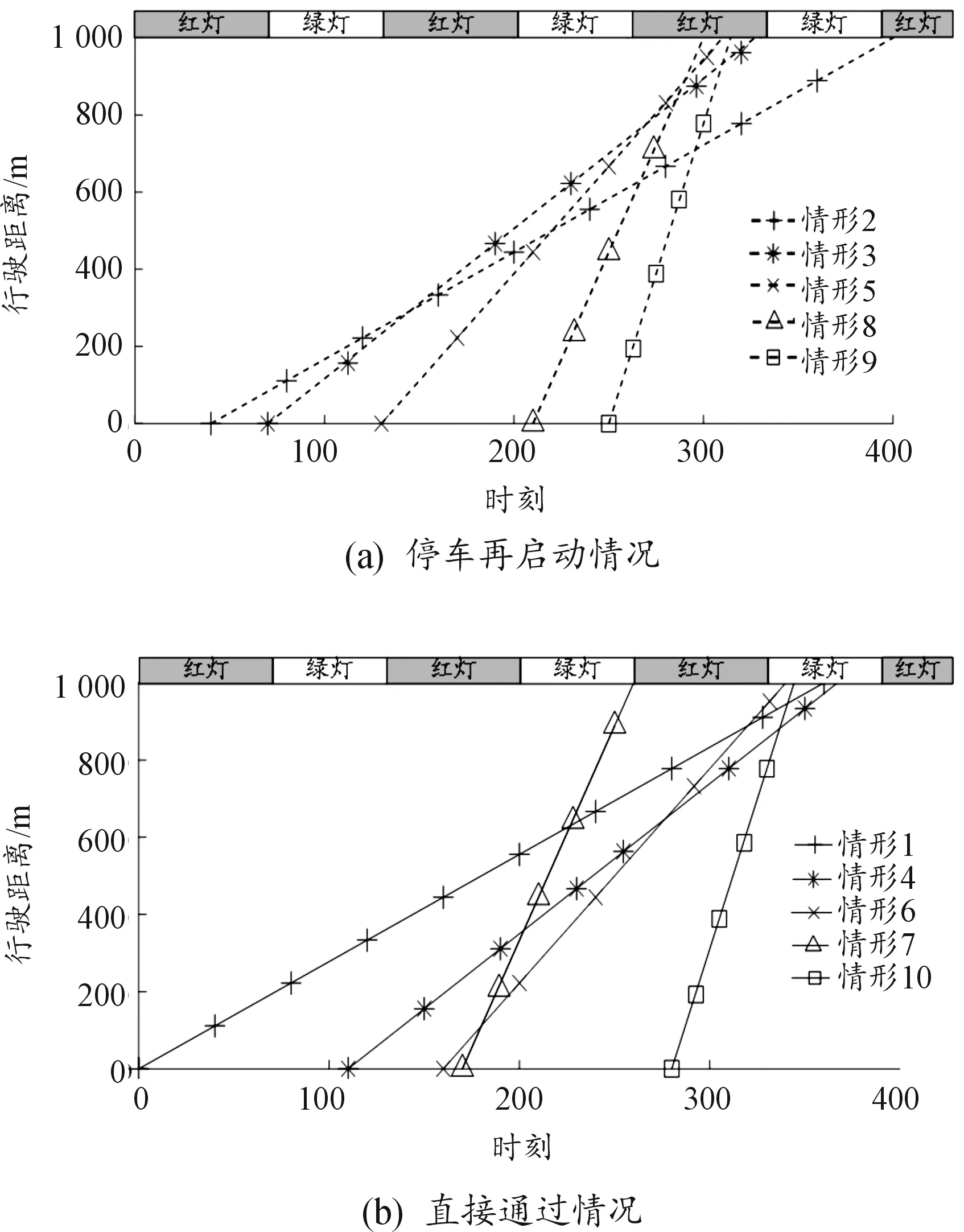
圖2 無車速引導情況下貨車時空軌跡圖

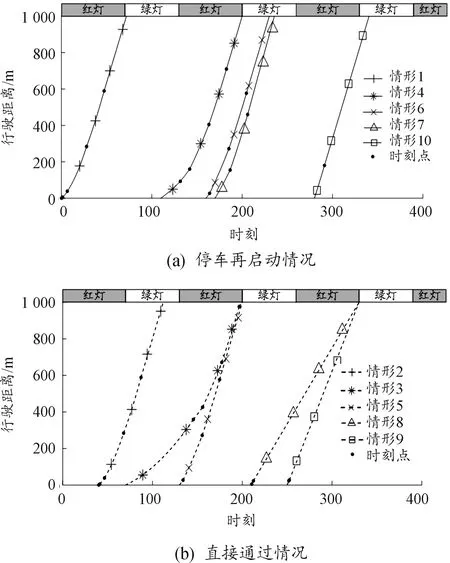
圖3 有車速引導情況下貨車時空軌跡圖

從圖2、3中可以看到：情形1、4、6、7、10屬于無車速引導時停車再啟動情況，情形2、3、5、8、9屬于無車速引導時直接通過情況。在有貨車車速引導的情況下，不論原速行駛時貨車是否在交叉口發(fā)生停車，其到達交叉口的時刻都有所提前。由于貨車停車再啟動消耗時間過長，貨車想要獲得最短的總行程時間就需要避免停車，理想狀態(tài)是一直以各擋位最大加速度加速至道路限速勻速通過路口，否則需要在綠燈開始時刻通過交叉口。

有車速引導情況下，情形1、2、6、7、10的時空軌跡圖就屬于一直以各擋位最大加速度加速至道路限速勻速通過路口情況，其到達交叉口的時刻未必是綠燈開始時刻。而情形3、4、5、8、9的時空軌跡圖在車速引導模型下在綠燈開始時刻通過交叉口，說明在以各擋位最大加速度加速至道路限速勻速行駛至交叉口時，信號燈為紅燈，則需要調(diào)整行駛軌跡，使得其在綠燈開始時刻通過交叉口。從無車速引導時停車再啟動情況與直接通過情況來看，無車速引導時發(fā)生停車的情形在有車速引導時可全部順利通過。因此當貨車車速引導模型給出準確合理的車速引導方案時，能夠在一定程度上減少交叉口停車等待次數(shù)和停車等待時間。

上述各情形仿真測試得出的有無車速引導方案行程總時間、停車時間及效果評價見表3和表4。

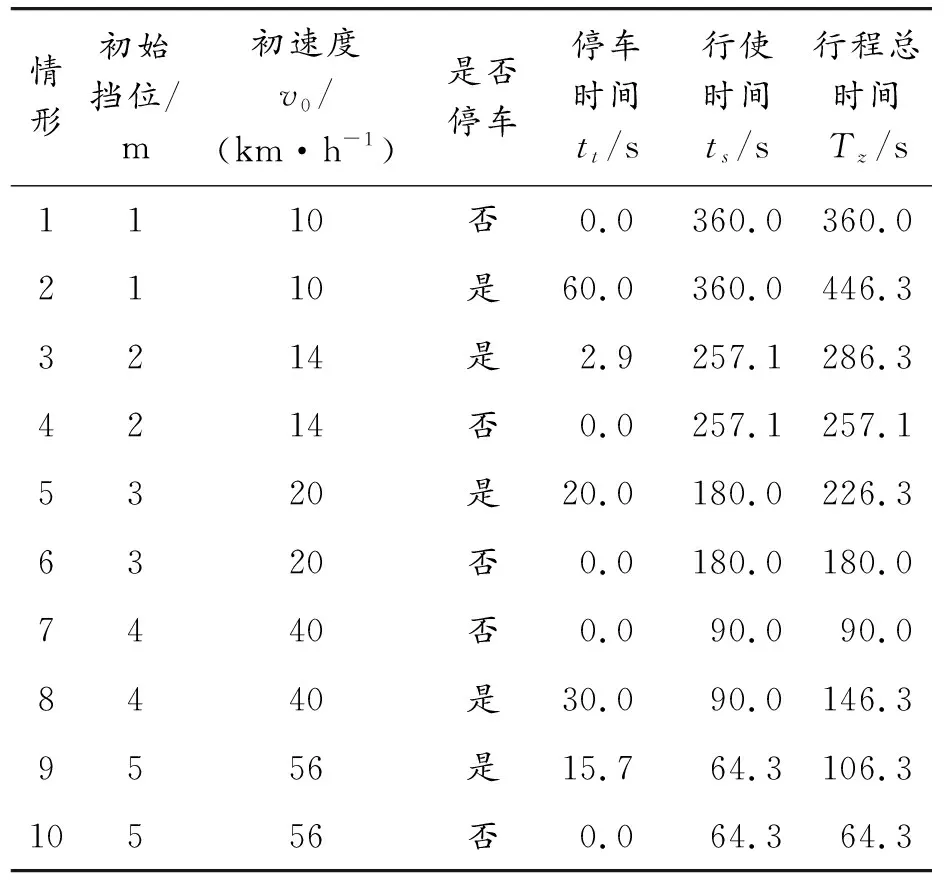
表3 無車速引導方案行程總時間和停車時間

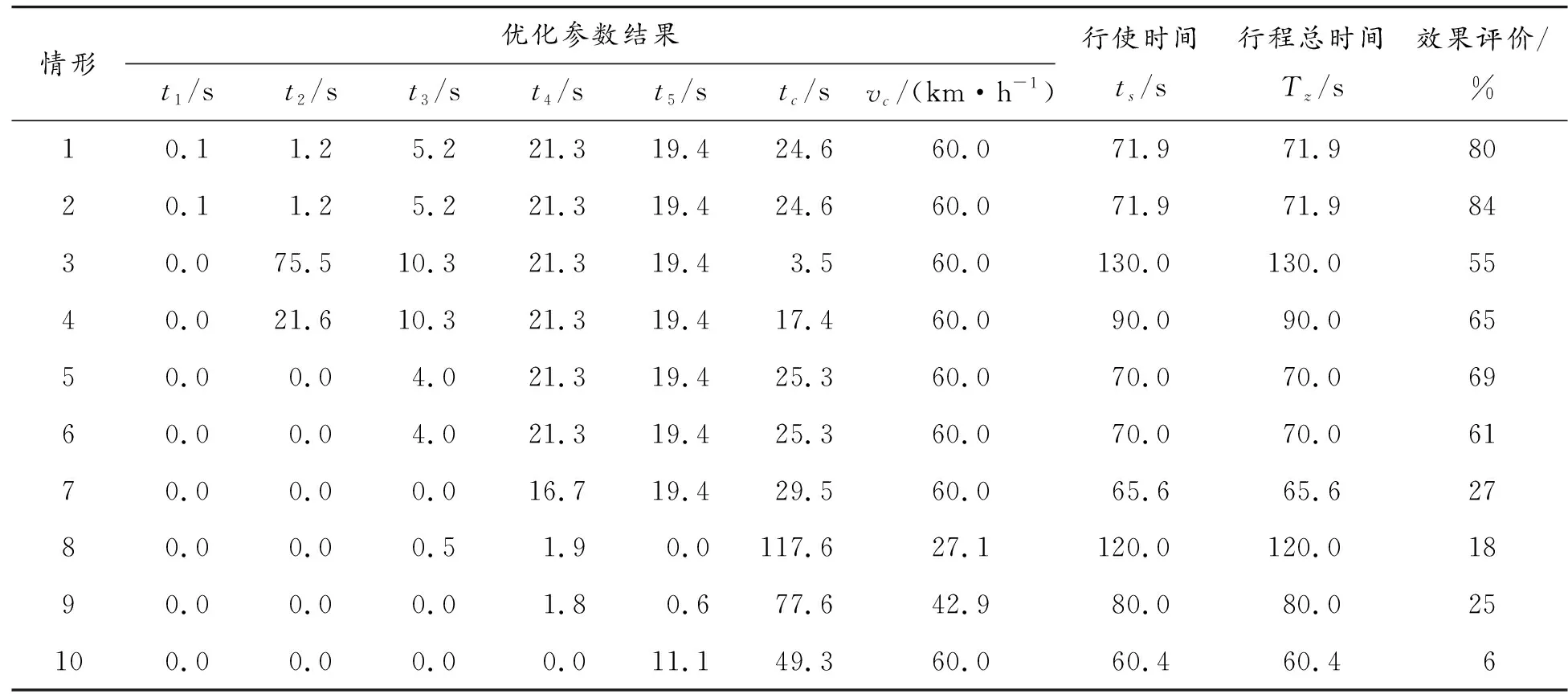
表4 有車速引導方案行程總時間及效果評價

可以看出，有車速引導模型的貨車總行程時間情形均低于無車速引導模型的情形。從不同擋位情況來看，1、2、3擋行駛速度貨車的總行程時間降低效果最好，可達61%～80%，這是因為如果駕駛員采取低擋位與低速度行駛至交叉口，不論是否存在停車再啟動時間和停車時間，其至交叉口的行駛時間都過長。4、5擋的總行程時間降低6%～27%。由此可以看出，貨車車速引導模型對于減少貨車的總行程時間起到了一定作用。

3 結論

1) 提出了一種車聯(lián)網(wǎng)環(huán)境下干線交叉口貨車車速引導模型，彌補了以往車速引導研究對引導車輛的加速度取值存在的不足，結合換擋操作對貨車各擋加速度限值進行計算來滿足貨車進行車速引導的約束條件。

2) 以總行程時間最短為目標進行車速引導建模，不僅減少了貨車總行程時間，還減少了交叉口停車次數(shù)，有助于降低貨車駕駛員勞動強度，可為貨車智能駕駛提供理論參考。

本研究只考慮了單輛貨車，未考慮車輛排隊等行為，尤其在交通流量較大的時候，很難達到貨車引導優(yōu)化模型所建議的行駛時間。后期將在此基礎上加入車輛排隊等模型，進一步完善車速引導模型。