初中生數(shù)學關鍵能力發(fā)展水平實證研究

武麗莎

初中生數(shù)學關鍵能力發(fā)展水平實證研究

武麗莎

（唐山師范學院 數(shù)學與計算科學學院，河北 唐山 063000）

初中生數(shù)學關鍵能力包括數(shù)學觀察、數(shù)學思考與數(shù)學表達三個測評維度，具體可以劃分為數(shù)學抽象能力、直觀想象能力、數(shù)學猜想能力、演繹論證能力、數(shù)據(jù)分析能力與模型運用能力等六個觀察指標。調查分析了四個城市334個初中生在數(shù)學關鍵能力上的表現(xiàn)，得出如下結論：初中生數(shù)學關鍵能力整體發(fā)展水平不理想，創(chuàng)新水平急需提升，初中生數(shù)學關鍵能力在測評維度與觀察指標上呈現(xiàn)多樣化的發(fā)展態(tài)勢。

數(shù)學關鍵能力；測評維度；觀察指標；發(fā)展水平

2017年9月，中共中央辦公廳、國務院辦公廳印發(fā)《關于深化教育體制機制改革的意見》，明確提出要重點培養(yǎng)學生的認知能力、合作能力、創(chuàng)新能力與職業(yè)能力。關鍵能力的形成需要借助不同學科的學習來實現(xiàn)，數(shù)學關鍵能力是關鍵能力在數(shù)學學科的體現(xiàn)，具有抽象性、嚴謹性與應用性的特征。隨著數(shù)學學科核心素養(yǎng)的提出，數(shù)學教育理念也從“以知識為本”轉向“以人為本”，尤其開始關注學生數(shù)學關鍵能力發(fā)展與培養(yǎng)。因此，本文從三個方面進行研究：初中生數(shù)學關鍵能力整體發(fā)展水平，初中生數(shù)學關鍵能力在測評維度以及各能力范疇的表現(xiàn)以及不同年級之間學生在數(shù)學關鍵能力上的差異性。

一、初中生數(shù)學關鍵能力測評框架

初中生數(shù)學關鍵能力測評框架是測試題編制的基礎，綜合考慮已有相關研究和《義務教育數(shù)學課程標準（2011年版）》（以下簡稱《課程標準（2011年版）》）的闡述，借助文獻法、專家咨詢法與訪談法，結合初中生的認知水平和數(shù)學課程要求，將初中生數(shù)學關鍵能力測評維度劃分為數(shù)學觀察能力、數(shù)學思考能力與數(shù)學表達能力。數(shù)學觀察能力指向學生能夠從數(shù)學的角度觀察世界，從而可以獲得相應的數(shù)學概念、數(shù)學規(guī)律、數(shù)學原理。數(shù)學觀察能力既是數(shù)學抽象的前提，也是提出問題的基礎，體現(xiàn)了數(shù)學的抽象性特征。數(shù)學思考能力指向學生能夠借助數(shù)學思維思考世界，這里的數(shù)學思維主要是指邏輯推理[1]，一方面，邏輯推理推動了數(shù)學學科的發(fā)展，使數(shù)學擺脫經驗層面的判斷，另一方面，邏輯推理從一些前提或者事實出發(fā)，依據(jù)一定的規(guī)則得到或者驗證命題，是得到數(shù)學命題與結論的重要途徑，數(shù)學思考能力體現(xiàn)了數(shù)學的嚴謹性特征。數(shù)學表達能力指向學生用數(shù)學語言描述世界，可以借助數(shù)學符號、數(shù)學模型、數(shù)據(jù)分析來刻畫數(shù)學對象的性質、關系和規(guī)律。隨著大數(shù)據(jù)時代的到來，數(shù)據(jù)分析變得越來越重要，學生應具備數(shù)據(jù)搜集、整理以及借助數(shù)據(jù)推斷數(shù)學規(guī)律的能力。數(shù)學表達能力體現(xiàn)了數(shù)學的廣泛應用性特征。

相關研究指出，高中生數(shù)學關鍵能力具體包括數(shù)學抽象能力、直觀想象與化歸能力、數(shù)學猜想與論證能力、數(shù)學運算能力、數(shù)據(jù)分析與預測能力、數(shù)學建模能力[2]。借鑒高中生數(shù)學關鍵能力成分的劃分，結合初中數(shù)學具體課程內容，經過討論與驗證，將初中生數(shù)學關鍵能力的三個測評維度細化：數(shù)學觀察包含數(shù)學抽象、直觀想象；數(shù)學思考包括數(shù)學猜想、演繹推理；數(shù)學表達包括數(shù)據(jù)分析、模型運用。喻平教授從知識學習視角將知識劃分為知識理解、知識遷移與知識創(chuàng)新[3]，以此對應學科關鍵能力的三級水平。本研究將數(shù)學關鍵能力劃分為理解、遷移與創(chuàng)新三個水平，形成初中生數(shù)學抽象能力三維度、三水平、六指標的測評框架，具體如表1所示。

表1 初中生數(shù)學關鍵能力測評框架

二、研究的設計與方法

（一）研究假設的厘定

本研究基于三個假設：首先，為考慮初中生數(shù)學關鍵能力的發(fā)展水平，將年級作為其主要影響因素，學生性別、教師素養(yǎng)、教學風格以及課外輔導因素不在本研究考慮范圍之內；其次，測試題在一定程度上可以反映初中生數(shù)學關鍵能力的各個水平；再次，初中生數(shù)學關鍵能力水平可以借助學生測試卷的分數(shù)來反映。

（二）研究方法的確定

根據(jù)初中生數(shù)學關鍵能力測評框架與研究假設，研究方法主要采用專家咨詢法與測驗法。

專家咨詢法用于對測試卷內容效度的檢驗，專家包括高等院校的數(shù)學教育理論研究者、初中數(shù)學教研員以及初中數(shù)學骨干教師。專家咨詢主要是從專家視角對測試題內容進行審視，例如測查重點是否合理、試題內容是否適切、試題項描述是否合規(guī)、試題難度是否合適等，不同結構專家既可以保證從測評理論方面進行指導，又能從教學實踐出發(fā)確保測試題的合理性與適切性。

測驗法即借助編制的測試題目，探究初中數(shù)學關鍵能力的整體發(fā)展狀況，考察不同年級的學生數(shù)學關鍵能力的各維度以及各指標的差異性，從而確定初中生數(shù)學關鍵能力的發(fā)展水平。

（三）研究樣本的選取

樣本選取遵循可行性與代表性原則。在選取學生樣本時，先確定學校，城市的經濟、教育發(fā)展水平，學校的師資、辦學條件等因素，將學校劃分為三類，即優(yōu)質學校、中等學校與薄弱學校，結合學緣、師緣、友緣等因素，選取唐山、天津、長春、東莞等城市學校的7～9年級學生。

由于7年級學生第一學期剛剛入學，因此在第二學期進行測查；考慮到學生中考的影響，9年級學生在第一學期結束時測查。共發(fā)放試卷356份，有效回收334份，有效率為93.8%，其中優(yōu)質學校學生樣本量112，中等學校學生樣本量為115，薄弱學校學生樣本量為107，學生樣本結構大體均衡。

（四）測評問卷的編制

采用自行設計的測驗卷對初中生數(shù)學關鍵能力進行測評，編制過程如下：

首先，明確測驗目的。這直接影響測試卷內容的難度、廣度以及測試題的類型選擇。本研究中，測驗的目的是考量初中生數(shù)學關鍵能力狀況，因此，圍繞能力取向編制問題，并且適當設置開放性問題；其次，采用雙向細目表的方式來呈現(xiàn)測驗藍本。由于測驗題量的限制，不可能完全兼顧初中所有數(shù)學內容，因此，通過專家咨詢，在選擇測試內容領域的時候遵循代表性原則、可行性原則、合理性原則與量力性原則；再次，編制測試題。題源主要是國內外已有研究中的測評題項、課程標準中的經典案例以及教材中的習題改編，盡量選取與初中數(shù)學知識相關性不大的內容編制測評試卷。

通過對56位專家咨詢，其中高校數(shù)學教育專家11位，初中數(shù)學教研員7位，初中數(shù)學骨干教師38位，發(fā)放問卷56份，回收有效問卷51份，有效率為91.1%，以此專家問卷數(shù)據(jù)為基礎，進行信度與效度檢驗，其中各個觀察指標信度如表2所示。初中生數(shù)學關鍵能力三個測評維度Cron- bach’s α系數(shù)均大于0.8，測試卷整體Cronbach’s α系數(shù)為0.883，信度較高。此外，數(shù)學關鍵能力觀察指標的Cronbach’s α系數(shù)在0.743- 0.891之間，均達到統(tǒng)計學標準，說明測試卷整體穩(wěn)定可靠。

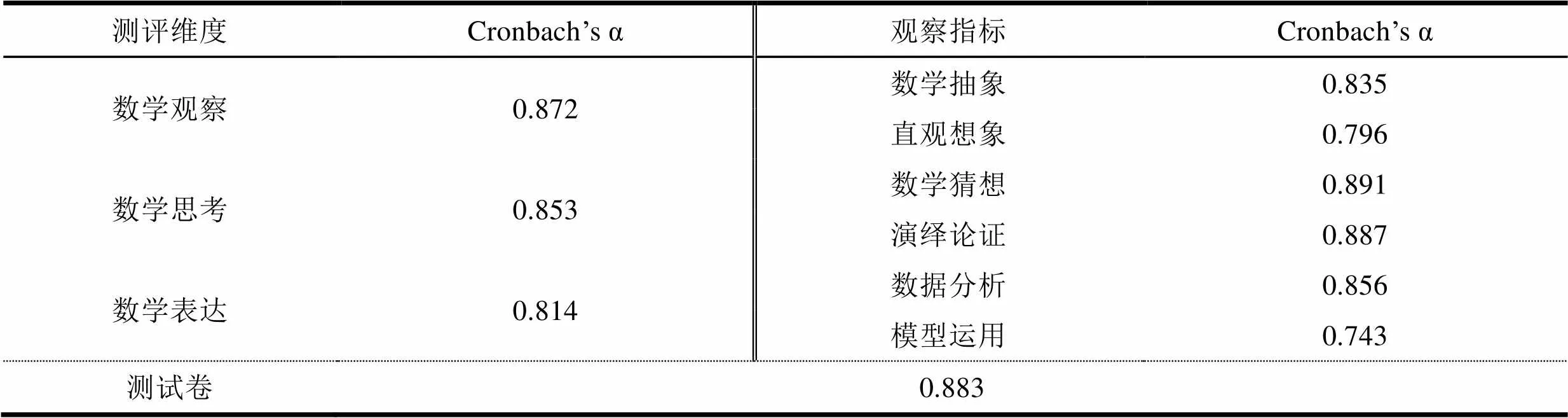
表2 初中生數(shù)學關鍵能力觀測維度與指標的Cronbach’s α系數(shù)

在結構效度上，根據(jù)杜克爾（Tuker）的理論，所需要的項目和測驗的相關應在0.30～0.80之間，項目間的組間相關在0.10～0.60之間，在這些相關全距之內的項目為測驗提供滿意的效度[4]。通過相關分析來檢驗各指標之間是否存在相關性，結果如表3所示，6個觀察指標之間的相關系數(shù)在0.156～0.361之間，呈現(xiàn)中度相關；各指標與總測試卷之間的相關系數(shù)在0.712～ 0.827之間，呈現(xiàn)高度相關。可以看出，總測試與各分測試題項的結構效度較好。

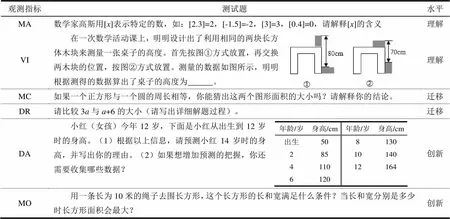
表4 初中生數(shù)學關鍵能力測試題枚舉

根據(jù)項目分析對測試卷進行三次調整，最終形成的測試卷中包含18個測評題項，每個觀察指標設計三個測試題，蘊含理解、遷移與創(chuàng)新三個層次，每個測評維度六個測試題，題目舉例如表4所示。

（五）數(shù)據(jù)分析的標準

本研究采取現(xiàn)場測查的方式，測試題由學生獨立完成，大約需50分鐘。學生測試問卷的評分由一名高校教師和兩名初中數(shù)學教師共同完成。首先，3名教師共同制定詳細的評分標準和細則，每道測評題項最低分為0分，最高分為3分，包含0、1、2、3四個分值，其中1分對應理解水平，2分對應遷移水平，3分對應創(chuàng)新水平，達到某個水平的標準按照60%來計算，問卷滿分為54分。該賦分方式直觀、簡潔，既可以體現(xiàn)能力，又能描述層次。然后，分別由兩名初中數(shù)學教師獨立完成評分，若產生分歧則由第三個教師進行仲裁，教師評分在95%以上一致，一致性程度較高。

三、研究結果分析

（一）初中生數(shù)學關鍵能力整體發(fā)展狀況

初中生數(shù)學關鍵能力整體發(fā)展狀況呈線性上升趨勢，如圖1所示。

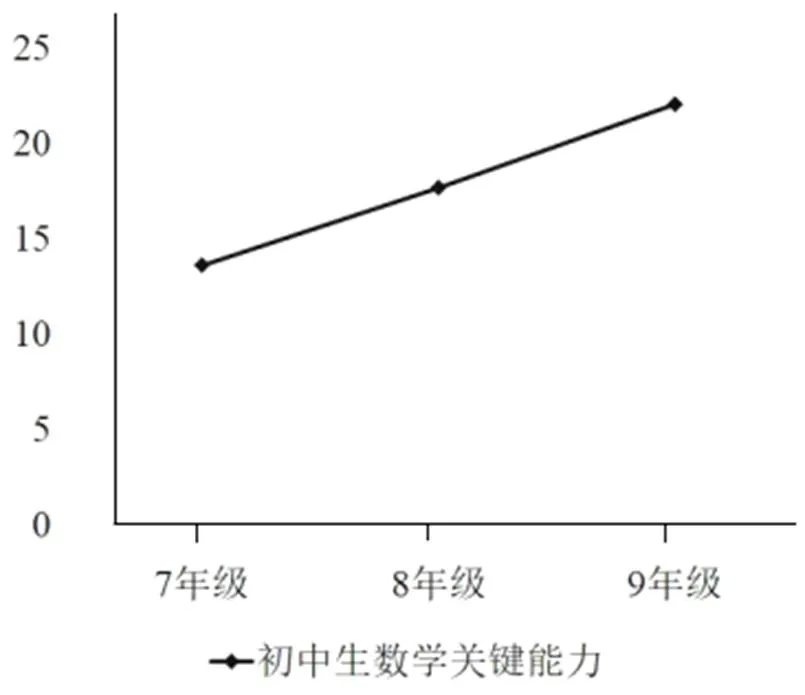
圖1 初中生數(shù)學關鍵能力整體發(fā)展狀況

7年級學生數(shù)學關鍵能力的平均分13.6分，得分率為25.2%，8年級學生數(shù)學關鍵能力的平均分17.7分，得分率為32.8%，9年級學生數(shù)學關鍵能力的平均分22.1分，得分率為40.9%。初中三個年級學生數(shù)學關鍵能力的得分率均未達到50%，按照60%的標準來看，初中三個年級學生數(shù)學關鍵能力總成績都沒有達到合格水平，7年級、8年級學生數(shù)學關鍵能力達到理解水平，9年級學生數(shù)學關鍵能力達到遷移水平，三個年級都沒有達到創(chuàng)新水平。

（二）初中生數(shù)學關鍵能力在各測評維度的發(fā)展狀況

初中三個年級學生數(shù)學關鍵能力在各測評維度的發(fā)展狀況如圖2所示。

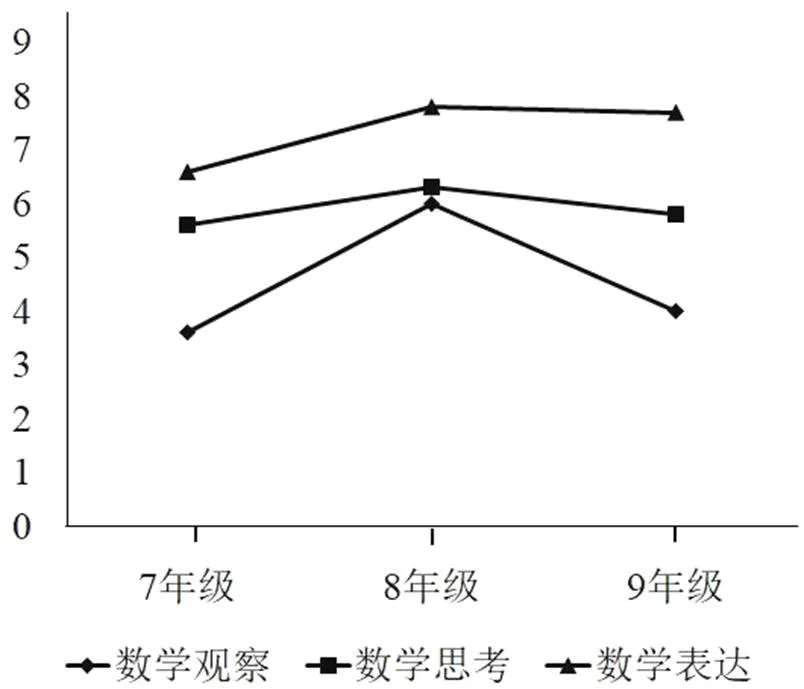
圖2 初中生數(shù)學關鍵能力各測評維度發(fā)展狀況

在數(shù)學觀察維度，7年級學生平均得分為3.6分，8年級學生平均得分為6.0分，9年級學生平均得分為4.0分；在數(shù)學思考維度，7年級學生平均得分為5.6分，8年級學生平均得分為6.3分，9年級學生平均得分為5.8分；在數(shù)學表達維度，7年級學生平均得分為6.6分，8年級學生平均得分為7.8分，9年級學生平均得分為7.7分。

從縱向來看，初中三個年級學生在3個測評維度的發(fā)展狀況呈現(xiàn)先增后降的變化趨勢，其中8年級學生得分高于7年級學生得分，這可能與學生在初中學習的適應性有關，同時，8年級學生得分高于9年級學生得分，這可能與9年級學生準備中考有關。

從橫向來看，在三個年級中，數(shù)學表達的得分最低，數(shù)學思考的得分最高，數(shù)學觀察得分居中，這也說明在《課程標準（2011年版）》的指引下，教師的課堂教學開始關注到了學生的數(shù)學思考。

（三）初中生數(shù)學關鍵能力在各觀察指標的發(fā)展狀況

初中三個年級學生數(shù)學關鍵能力在各觀測指標的發(fā)展趨勢各不相同，具體如圖3所示。

從圖3可以看出，初中生數(shù)學關鍵能力在各觀察指標的發(fā)展狀況分為三種類型，一是先增后降，二是逐漸遞增，三是先降后增，其中，數(shù)學抽象能力屬于先增后降型，數(shù)學猜想能力屬于先降后增型，直觀想象、演繹論證、數(shù)據(jù)分析、模型運用四個能力屬于逐漸遞增型。在數(shù)學抽象能力方面，7年級學生平均得分為2.3分，8年級學生平均得分為3.1分，9年級學生平均得分為2.6分，這樣的變化可能是因為數(shù)學抽象更多是呈現(xiàn)在課堂教學中，幫助學生形成數(shù)學概念與規(guī)律，9年級由于處于中考準備階段，不再關注數(shù)學概念的形成。

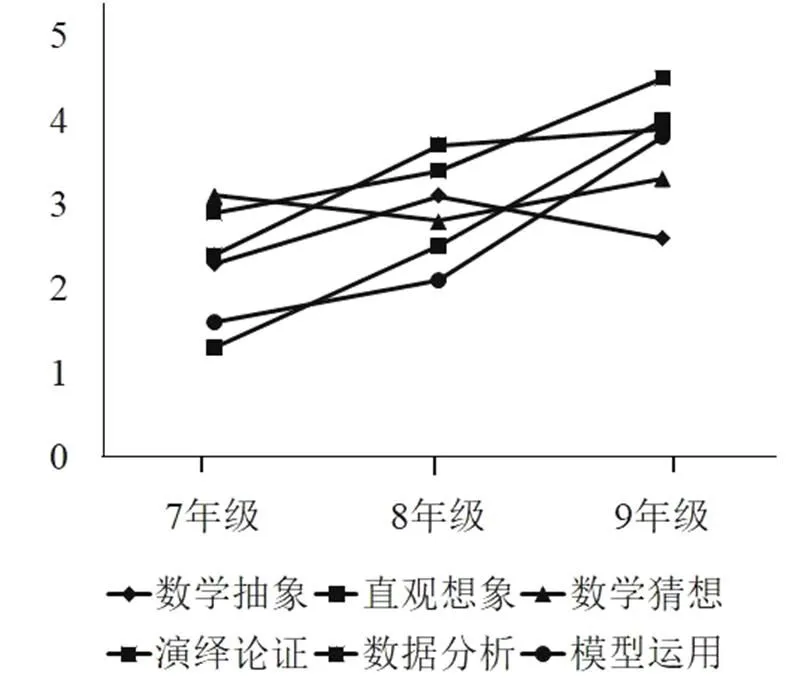
圖3 初中生數(shù)學關鍵能力各觀測指標發(fā)展狀況

在直觀想象能力方面，7年級學生平均得分為1.3分，8年級學生平均得分為2.5分，9年級學生平均得分為4.0分；在數(shù)學猜想能力方面，7年級學生平均得分為3.1分，8年級學生平均得分為2.8分，9年級學生平均得分為3.3分，這可能因為小學階段比較注重學生的數(shù)學猜想，更多是通過找規(guī)律的內容來呈現(xiàn)，而初中階段的教學更多關注邏輯推演，從而導致數(shù)學猜想能力的下降。

在演繹論證能力方面，7年級學生平均得分為2.9分，8年級學生平均得分為3.4分，9年級學生平均得分為4.5分。在數(shù)據(jù)分析能力方面，7年級學生平均得分為2.4分，8年級學生平均得分為3.7分，9年級學生平均得分為3.9分。

在模型運用能力方面，7年級學生平均得分為1.6分，8年級學生平均得分為2.1分，9年級學生平均得分為3.8分。

根據(jù)60%的標準，在六個觀察指標上，三個年級學生均未達到創(chuàng)新水平。在數(shù)學抽象能力、數(shù)學猜想能力、演繹論證能力與數(shù)據(jù)分析能力方面，三個年級學生都達到理解水平，均未達到遷移水平；在直觀想象能力方面，7年級學生沒有達到理解水平，8年級學生達到理解水平，9年級學生達到遷移水平；在模型運用能力方面，7年級與8年級學生未達到理解水平，9年級學生達到遷移水平。

（四）不同年級學生在數(shù)學關鍵能力各測評維度上的差異分析

在了解初中生數(shù)學關鍵能力整體發(fā)展狀況基礎上，對于不同年級學生在數(shù)學關鍵能力各測評維度進行方差分析，其方差檢驗結果如表5所示。

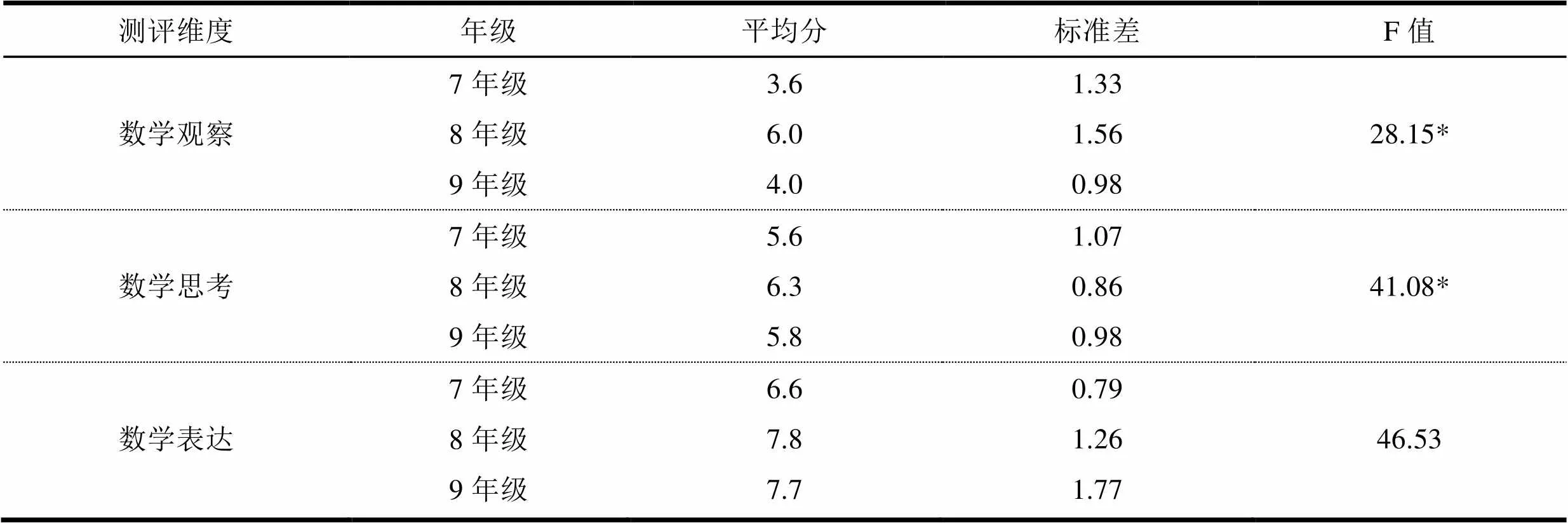
表5 不同年級的學生在測評維度上的差異

注：*表示p<0.05

不同年級學生在數(shù)學觀察、數(shù)學思考、數(shù)學表達方面存在顯著差異。為進一步說明兩個年級之間在測評維度上的具體差異，采用LSD法進行多重比較。

在數(shù)學觀察維度上，7年級與8年級學生之間存在顯著差異（p=0.007<0.05），7年級與9年級學生之間不存在顯著差異（p=0.271>0.05），8年級與9年級學生之間存在顯著差異（p=0.000<0.05）；在數(shù)學思考維度，7年級與8年級學生之間存在顯著差異（p=0.012<0.05），7年級與9年級學生之間不存在顯著差異（p=0.165>0.05），8年級與9年級學生之間存在顯著差異（p=0.005<0.05）；在數(shù)學表達維度，7年級與8年級學生之間存在顯著差異（p=0.007<0.05），7年級與9年級學生之間存在顯著差異（p=0.011<0.05），8年級與9年級學生之間存在顯著差異（p=0.000<0.05）。

（五）不同年級學生在數(shù)學關鍵能力各觀察指標上的差異分析

為了解不同年級學生在數(shù)學關鍵能力各觀測指標上的差異，對三個年級學生數(shù)學關鍵能力六個觀察指標進行方差分析。從表6可以看出，不同年級學生在數(shù)學關鍵能力的六個觀測指標都存在顯著差異。下面采用LSD法進行多重比較。

在數(shù)學抽象能力上，7年級與8年級之間存在顯著差異（p=0.000<0.05），7年級與9年級之間不存在顯著差異（p=0.121>0.05），8年級與9年級學生之間存在顯著差異（p=0.016<0.05）。

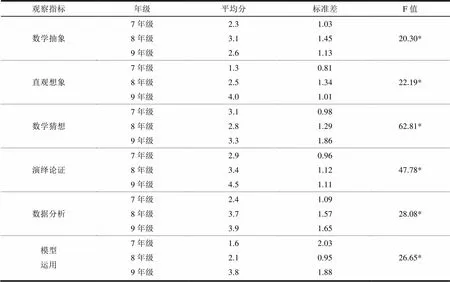
表6 不同年級的學生在觀測指標上的差異

注：*表示p<0.05

在直觀想象能力上，7年級與8年級之間存在顯著差異（p=0.010<0.05），7年級與9年級之間存在顯著差異（p=0.023<0.05），8年級與9年級學生之間存在顯著差異（p=0.004<0.05）。

在數(shù)學猜想能力上，7年級與8年級之間不存在顯著差異（p=0.105>0.05），7年級與9年級之間存在顯著差異（p=0.000<0.05），8年級與9年級學生之間存在顯著差異（p=0.024<0.05）。

在演繹論證能力上，7年級與8年級之間存在顯著差異（p=0.046<0.05），7年級與9年級之間存在顯著差異（p=0.018>0.05），8年級與9年級學生之間存在顯著差異（p=0.000<0.05）。

在數(shù)據(jù)分析能力上，7年級與8年級之間存在顯著差異（p=0.000<0.05），7年級與9年級之間存在顯著差異（p=0.000<0.05），8年級與9年級學生之間不存在顯著差異（p=0.217<0.05）。

在模型運用能力上，7年級與8年級之間存在顯著差異（p=0.031<0.05），7年級與9年級之間存在顯著差異（p=0.000<0.05），8年級與9年級學生之間存在顯著差異（p=0.000<0.05）。

四、研究結論與討論

（一）初中生數(shù)學關鍵能力整體的發(fā)展水平不理想

從初中生數(shù)學關鍵能力測查成績來看，學生數(shù)學關鍵能力整體發(fā)展水平偏低，三個年級的得分率均未達到50%。一方面，義務教育課程標準還在修訂中，目前的教學依據(jù)的是《課程標準（2011年版）》，在標準中也沒有明確提及數(shù)學關鍵能力，因此，可能導致教師在教學中還沒有足夠重視學生數(shù)學關鍵能力的培養(yǎng)；另一方面，義務教育長期受到基礎知識與基本技能的影響，無論是教學，還是評價，考試重點成為教學的重要指引，與能力相比，更關注知識的測評。從高中數(shù)學課程標準來看，數(shù)學關鍵能力是非常重要的考核目標，義務教育數(shù)學課程標準的修訂也應將其作為主要的目標導向，隨著新版義務教育課程標準的頒布與實施，初中生數(shù)學關鍵能力的水平可能會有所提升。

（二）初中生數(shù)學關鍵能力的創(chuàng)新水平亟待提升

在所選樣本中，無論是測評維度還是觀察指標，三個年級學生的數(shù)學關鍵能力均未達到創(chuàng)新水平，初中生數(shù)學關鍵能力的創(chuàng)新水平急需提升。近年來，數(shù)學教育提倡創(chuàng)新能力，《課程標準（2011年版）》更是將創(chuàng)新意識作為十大核心概念，要求學生在數(shù)學學習過程中，發(fā)現(xiàn)和提出數(shù)學問題，這應貫穿整個義務教育階段。

創(chuàng)新涵蓋三個層面的內涵，第一層內涵是學生能對教學內容作適當?shù)耐卣古c延伸，第二層內涵是能對問題進行推廣與變式，第三層內涵是學生能夠形成學科思維[3]。從學生回答問題來看，創(chuàng)新第一層內涵表現(xiàn)得就不夠好，學生難以對所學內容進行拓展與延伸，因此，加強初中數(shù)學學習的拓展與延伸，是提升其數(shù)學關鍵能力創(chuàng)新水平的第一步。

（三）初中生數(shù)學關鍵能力的發(fā)展態(tài)勢呈現(xiàn)多樣化

初中生數(shù)學關鍵能力在測評維度與觀察指標上都呈現(xiàn)出多樣化的發(fā)展狀況。首先，在測評維度上，初中生數(shù)學思考要遠遠高于數(shù)學觀察，這也解釋了學生難以在實際情境中獲取數(shù)學概念，提出數(shù)學問題，這都與缺少數(shù)學觀察有關；其次，在觀察指標上，從學生的測查成績來看，三個年級學生在各觀察指標上的表現(xiàn)差異較大，在各指標的變化上呈現(xiàn)先增后減、先減后增、逐漸遞增三種類型，可以根據(jù)各種類型，找到初中生數(shù)學關鍵能力的重要節(jié)點，關注小學與初中在數(shù)學教學的銜接，遵循其年級特征，制定有針對性的教學設計，選擇適當?shù)慕虒W方法，這對于促進初中生數(shù)學關鍵能力的發(fā)展具有一定的指導意義。

[1] 史寧中,林玉慈,陶劍,郭民.關于高中數(shù)學教育中的數(shù)學核心素養(yǎng)——史寧中教授訪談之七[J].課程·教材·教法, 2017,37(4):8-14.

[2] 朱立明.高中生數(shù)學關鍵能力測評指標體系的構建[J].課程·教材·教法,2020,40(3):34-42.

[3] 喻平.學科關鍵能力的生成與評價[J].教育學報,2018, 14(2):34-40.

[4] 劉婷,陳倩.高中生訂正數(shù)學錯題態(tài)度量表的編制和檢驗[J].數(shù)學教育學報,2019,28(1):30-36.

An Empirical Study on the Development Level of Junior Middle School Students' Mathematics Key Ability

WU Li-sha

(School of Mathematics and Computational Sciences, Tangshan Normal University, Tangshan 063000, China)

The key mathematical ability of junior high school students includes three measurement dimensions: mathematical observation, mathematical thinking and mathematical expression, which can be divided into six observation indexes: mathematical abstraction ability, intuitive imagination ability, mathematical guess ability, deductive demonstration ability, data analysis ability and model application ability. The performances of key mathematical ability of 334 junior high school students in 4 cities are investigated and analyzed. The conclusion is as follows: The overall development level of junior high school students’ key mathematical ability is relatively low. Their innovation level needs to be improved urgently. The development trend of junior high school students’ mathematics key ability is diversified in the measurement dimension and observation index.

key mathematical ability; measurement dimension; observation index; level of development

G625.5

A

1009-9115(2021)05-0154-07

10.3969/j.issn.1009-9115.2021.05.028

唐山市人才資助項目（A202002033），唐山師范學院教育教學改革研究項目（2018001003）

2021-02-24

2021-08-09

武麗莎（1986-），女，河北唐山人，碩士，講師，研究方向為數(shù)學教育。

（責任編輯、校對：高俊霞）