考慮隨機生產等待的串行生產系統機會維護建模

寧小涵， 周曉軍

(上海交通大學 機械與動力工程學院，上海 200240)

維護是保障生產系統正常運行、提高設備可靠性的有效手段.隨著市場需求的日趨多樣化，越來越多的制造企業采用面向訂單的生產模式.在這一模式下，由于原材料缺乏、需求不足等原因，生產系統常面臨著隨機的生產等待，進而導致系統整體停機，這也為系統維護帶來了機會.為此，如何充分利用隨機生產等待以合理優化系統的維護方案，對制造企業降低維護成本、提高生產效率有重要的現實意義.

目前，已有的機會維護研究多圍繞如何利用系統中設備強制預防維護所引發的確定性停機時間進行機會維護.Xia等[1]采用單維護時間窗方法判斷串行系統中的設備是否接受預先計劃的確定性預防維護機會，并對維護活動進行整合優化.俞夢琦等[2]則引入雙維護時間窗方法進一步確定維護組合的最佳維護時刻.Zhou等[3]、Zhao等[4]和Nguyen等[5]基于設備的狀態判斷其是否接受這種確定性機會.Zhou等[6]以最大化短期機會費用節余為目標，采用動態規劃求解，判斷是否接受強制預防維護引發的機會.顯然，已有研究均集中于如何利用設備強制預防維護所引發的系統內部維護機會，沒有考慮生產等待帶來的外部維護機會，不利于進一步降低維護成本.

在利用外部機會的機會維護研究中，先期有學者針對確定性的外部機會進行研究.Do van等[7]針對多設備串聯系統提出新的動態成組維護策略，對預先已知的外部機會進行維護活動規劃.Nzukam 等[8]基于Bruss算法選擇最優的外部機會對單設備系統進行機會維護.Khatab等[9]考慮利用生產計劃中預先已知的生產間歇進行機會維護，提出基于彈性維護力度的串并聯系統選擇性維護優化模型.隨著市場需求的多樣化，生產等待的隨機性越來越高，為此，Li等[10]提出基于年齡的單設備更換策略，隨機生產等待到達時，若設備年齡達到機會更換閾值則對其進行更換.Wu等[11]提出兩階段單設備機會維護策略，第1階段對設備進行等周期檢測，第2階段利用隨機到達的生產等待進行機會維護，以充分利用設備剩余壽命.Yang等[12]采用逆高斯分布來表示設備衰退增量，針對生產等待隨機到達的單設備系統，基于狀態維護與機會維護相結合的策略，獲得預防更換衰退閾值和機會更換衰退閾值.在考慮機會到達隨機性的基礎上，Truong等[13-14]還考慮機會持續時間的隨機性，提出基于時變持續時間閾值的單設備機會維護策略.綜合來說，由于隨機性導致決策過程復雜，目前對利用隨機外部機會進行機會維護的研究多局限于單設備維護規劃層面，且沒有兼顧系統中其余設備強制預防維護帶來的內部機會.

本文以多設備串行生產系統為研究對象，考慮齊次泊松到達且持續時間隨機的生產等待，提出一種時間窗與引力窗相結合的維護決策模型，充分利用了生產等待帶來的外部維護機會以及系統中設備強制預防維護引發的內部維護機會實施維護優化，以獲取系統在維護規劃期內的最優維護計劃，為面臨隨機生產等待的串行系統維護決策優化研究提供基礎.

1 問題描述及維護策略

串行生產線中的生產等待如圖1所示，該生產線由n臺設備組成.以串行生產系統為研究對象，在實際生產場景中，該生產線面臨隨機到達的生產等待且持續時間隨機.通常，串行生產系統中任何一臺設備的停機往往意味著系統的整體停機，為了減少設備維護造成的停機時間，節約停機成本，可利用生產等待帶來的外部機會對生產線進行維護.

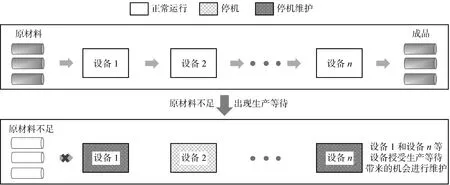
圖1 串行生產線中的生產等待Fig.1 Production waits in serial production line

在維護策略方面，對于串行生產系統中的每一臺設備，當出現可接受的生產等待時，該設備實施機會維護；若在計劃的預防維護周期內沒有生產等待被接受，則進行預防維護；設備發生故障時，則進行故障小修.從整個系統的角度考慮，設備的同時維護也意味著系統停機成本的節約，故當某些設備停機進行機會維護或預防維護時，其余設備也存在著提前維護的內部機會.對于由設備強制預防維護(內部機會)引發的維護活動，采用時間窗[1]判斷其余設備是否同時維護；而對于由設備接受生產等待(外部機會)引發的維護活動，由于每個設備進行維護的時刻并不固定，傳統時間窗無法有效組合這類維護活動，所以引入引力窗判斷未接受生產等待機會的設備是否同時維護.

基于以上維護策略，維護建模及決策分為兩部分.首先，建立一個隨機狀態下的設備層維護決策優化模型，分別構建機會維護和預防維護的期望維護成本模型，以最小化各維護周期內各設備期望維修總成本率為目標，獲得最優設備時間窗和生產等待持續時間閾值并判斷是否接受生產等待的機會；其次，構建綜合考慮內部機會和外部機會的系統層維護決策優化模型，以最小化維護規劃期內系統維護總成本率為目標，基于系統時間窗與引力窗相結合的維護模型獲得系統的最優維護計劃.其中，引力窗的定義綜合考慮了機會到達時刻與持續時間、設備維護相關成本及機會與設備時間窗之間的關系對于系統層維護整合趨向的影響.

2 維護建模及決策

2.1 考慮隨機生產等待的單設備維護建模及決策

考慮到模型的復雜性，首先提出以下假設：① 預防維護與機會維護均為修復非新，且效果相同；② 故障小修僅恢復設備功能不改變其衰退狀況；③ 維護活動和生產等待的持續時間相比于維護周期很短，故忽略不記；④ 生產等待到達服從齊次泊松過程，持續時間為已知分布的隨機變量[10-13].

預防維護和機會維護往往不會使設備恢復到全新狀態.Pham等[15]概括總結了8種修復非新的建模方法，其中虛擬役齡法在工程實踐中應用廣泛，故基于該建模思想，采用虛擬役齡描述設備狀態，并用虛擬役齡因子θ∈(0,1)表示維護設備健康衰退演化的影響，則第i臺設備在第j+1次維護后的虛擬役齡Ai,j+1為

Ai,j+1=Ai,j+θiTi,j+1

(1)

式中：θi為第i臺設備的虛擬役齡因子；Ti,j+1為第i臺設備第j+1個維護周期的長度.

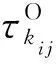
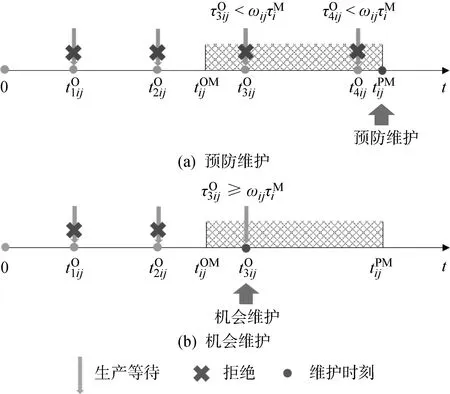
圖2 設備維護的兩種情況Fig.2 Two situations of equipment maintenance

(2)

預防維護總成本包括維護成本、停機成本和故障小修成本，故第i臺設備在第j個維護周期預防維護的期望維修成本率為

(3)

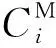
(4)

(5)

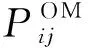
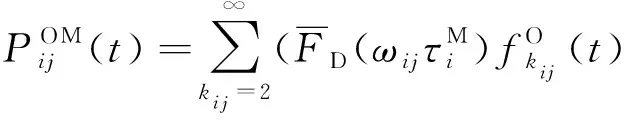
(6)

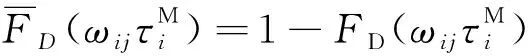
(7)

(8)

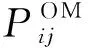
(9)

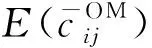
(10)

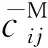
(11)

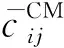
(12)

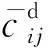
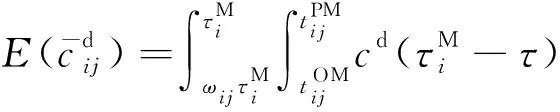
(13)

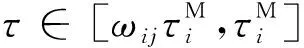
(14)

(15)

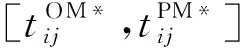
2.2 時間窗與引力窗相結合的系統維護建模及決策

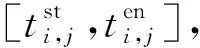
(16)

(17)

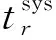
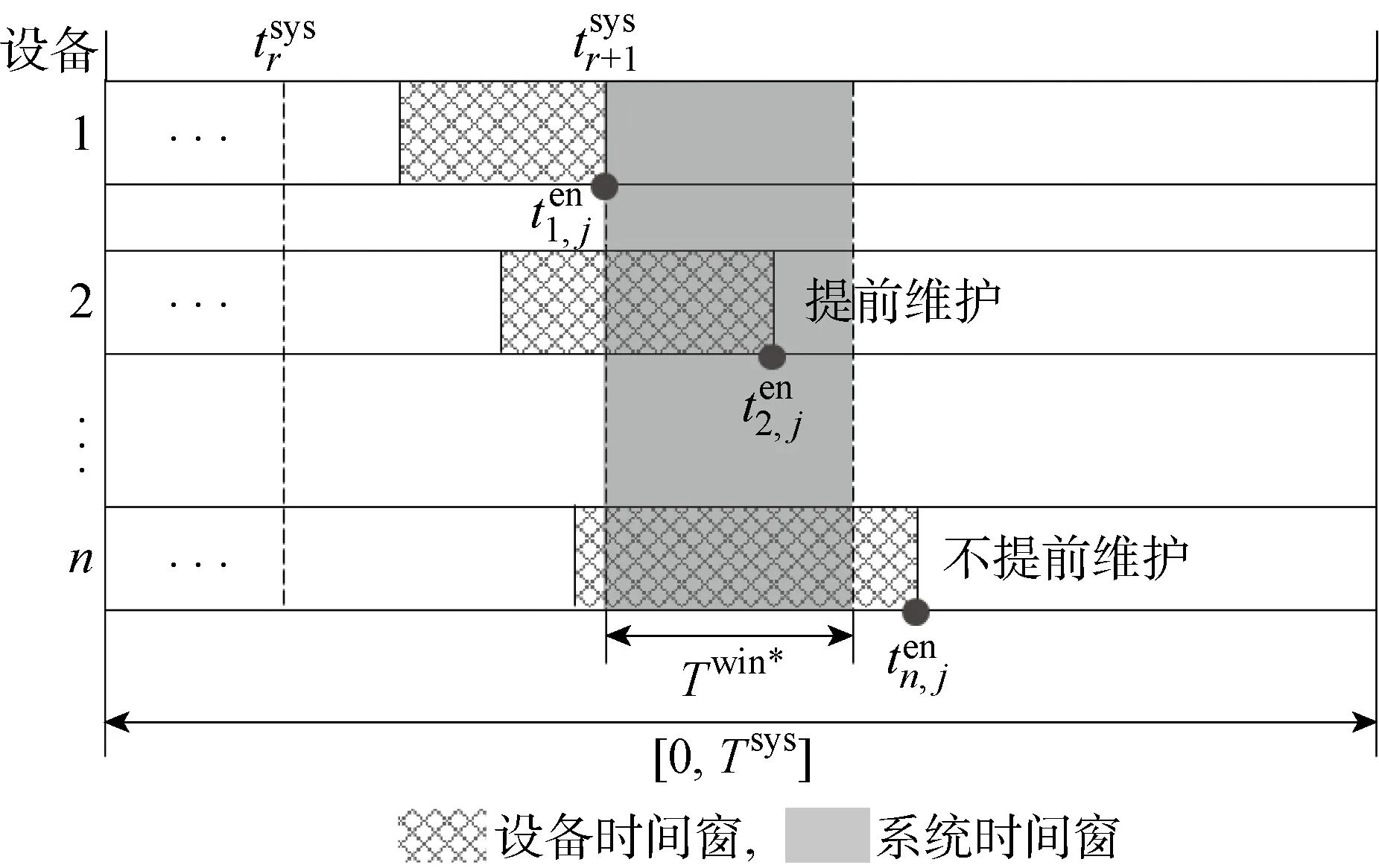
圖3 針對強制預防維護的時間窗模型Fig.3 Time window model for mandatory preventive maintenances

而對于外部機會(接受生產等待)引發的系統維護活動，由于每個設備都分別通過設備時間窗判斷是否接受生產等待的機會，而不是在一個計劃的時間點進行維護，系統時間窗無法處理這類維護活動的優化整合，所以引入引力窗這一概念來進一步對維護活動進行優化整合.

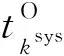
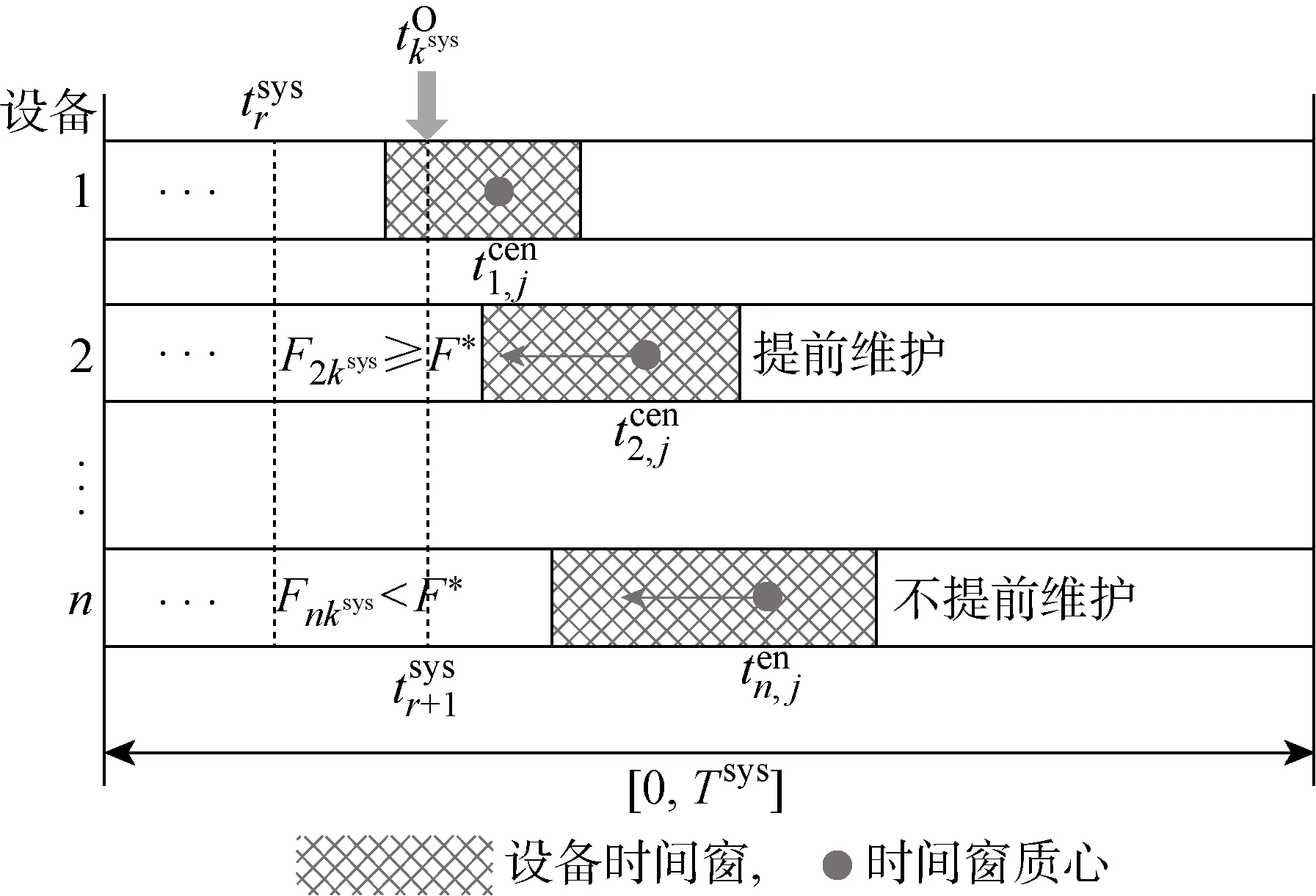
圖4 針對隨機生產等待的引力窗模型Fig.4 Gravity window model for stochastic production waits

類比于萬有引力公式Fiksys可以定義為

(18)

式中：G為引力常量；miksys為機會的“質量”；Mi為第i臺設備時間窗的“質量”；Riksys為機會與設備時間窗之間的“距離”.將萬有引力公式與機會維護策略相結合的關鍵在于如何定義以上“質量”和“距離”.引力常量G是一個比例系數，為了計算方便，取為G=1 N·h2/元2；“質量”表示維護整合趨向的大小.機會的持續時間和設備的停機成本影響這一趨向的大小，故機會的“質量”miksys可定義為

(19)

(20)

(21)

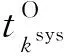
(22)

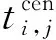
(23)

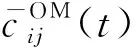
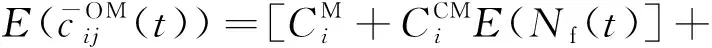
(24)

基于以上所述的系統維護整合模型，具體決策步驟如下.

步驟1從系統初始活動次數，即r=1開始，各設備處于全新狀態；

步驟2輸入各設備維護時間窗及質心，并賦值給3個時刻tst、ten和tcen，即

步驟3判斷累計系統維護活動次數是否達到維護規劃期Tsys.若是，結束系統維護規劃；否則，轉入步驟4；

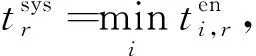
(25)

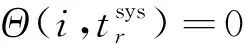
(26)

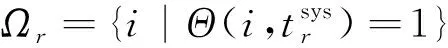
(27)

步驟5進入下一次維護活動，賦值r=r+1，則

(28)

i=1,2,…,n

(29)

i=1,2,…,n

(30)

i=1,2,…,n

然后轉回步驟3進行下一次維護活動的維護規劃.

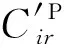
(31)

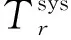
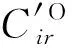
(32)

3 算例分析

3.1 算例概覽及策略對比

考慮一個由6臺串行設備組成的機械加工生產線，如車床、磨床、銑床等組成的串行生產系統，生產線維護規劃期Tsys=1 500 h.Weibull分布特別適用于機械加工設備的故障率建模，故假設該串行生產線中每臺設備的故障率分布均服從Weibull分布，即為

(33)

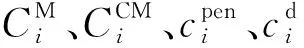
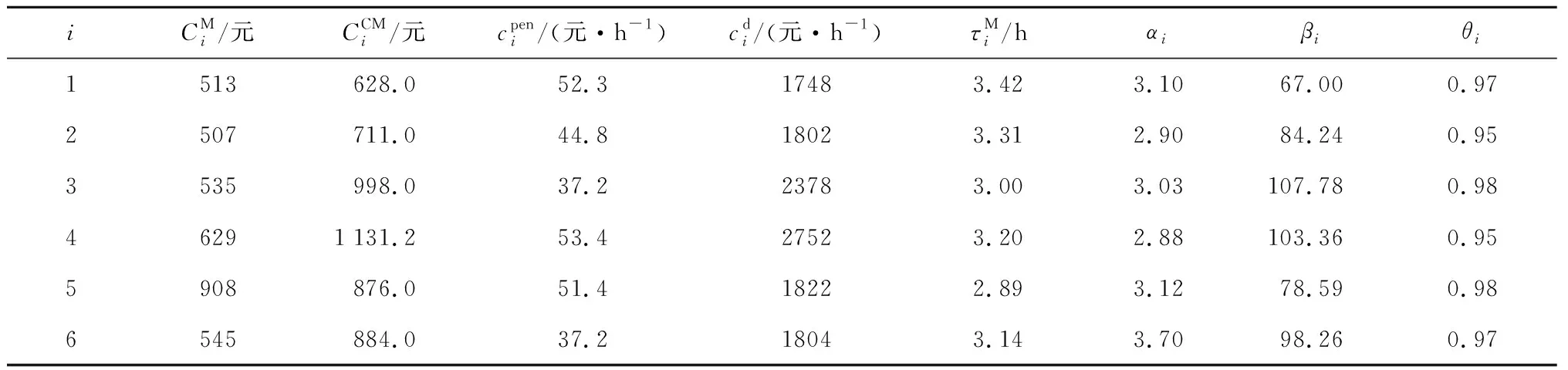
表1 設備參數Tab.1 Equipment parameters

為獲得時間窗和引力窗維護整合模型下系統的最優維護策略，基于MATLAB對系統進行仿真，系統維護模型的決策變量為Twin*和F*.Twin*取值以設備預防維護周期為依據，通過設備層的數值模擬得到系統中設備的最長預防維護周期約為250 h，因此Twin*的搜索范圍為[0,250] h，搜索步長為10 h，通過仿真得到F*的最優取值落在[3,9] kN區間內，即為搜索范圍，搜索步長為0.1 kN.生產等待的隨機性給系統帶來了不確定性，因此利用仿真獲得系統平均總維護成本率，每次數值模擬均對系統做 2 000 次隨機場景中的仿真.

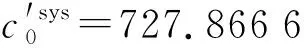
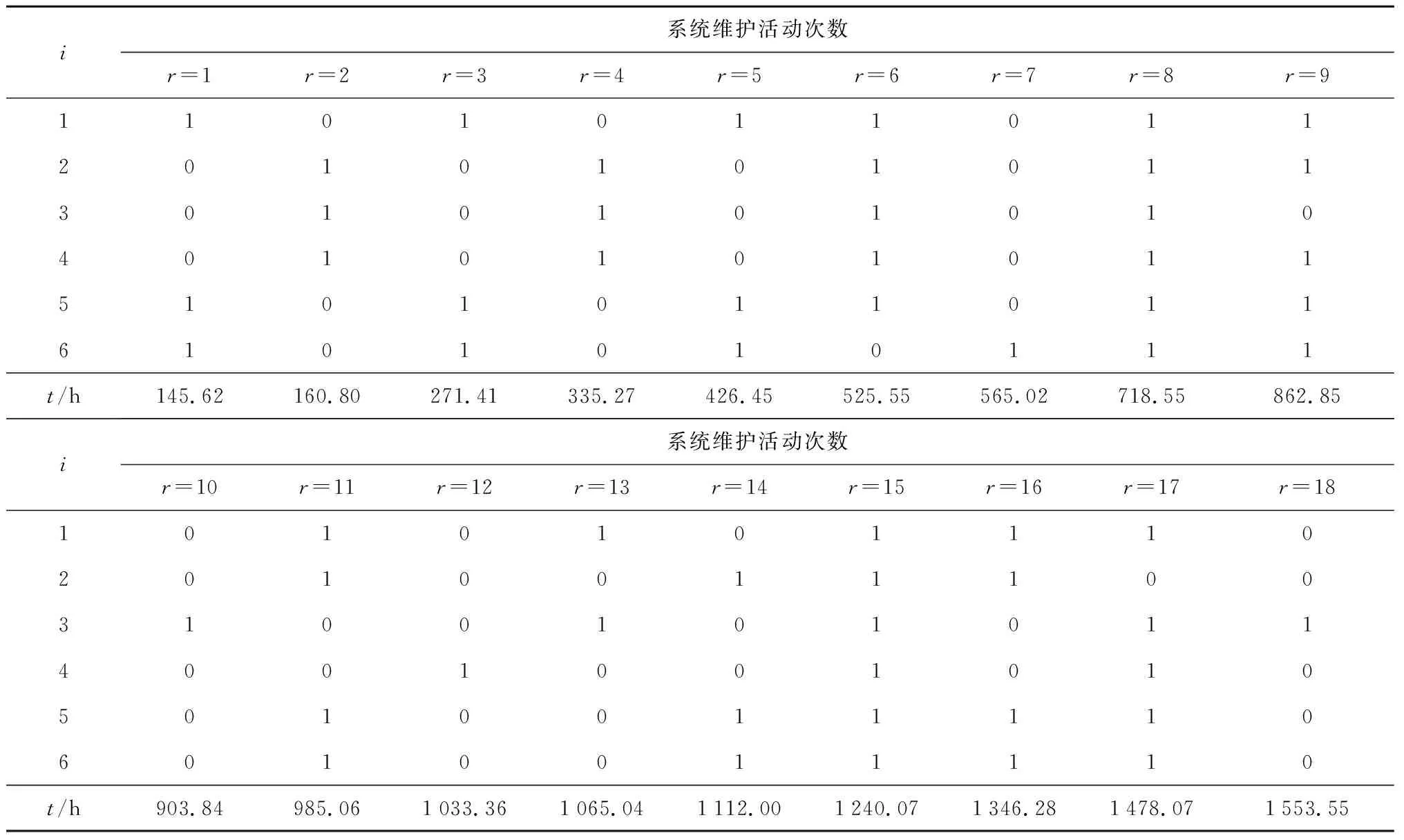
表2 系統維護時刻表Tab.2 System maintenance schedule

3.2 不同停機成本下的策略對比

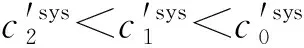
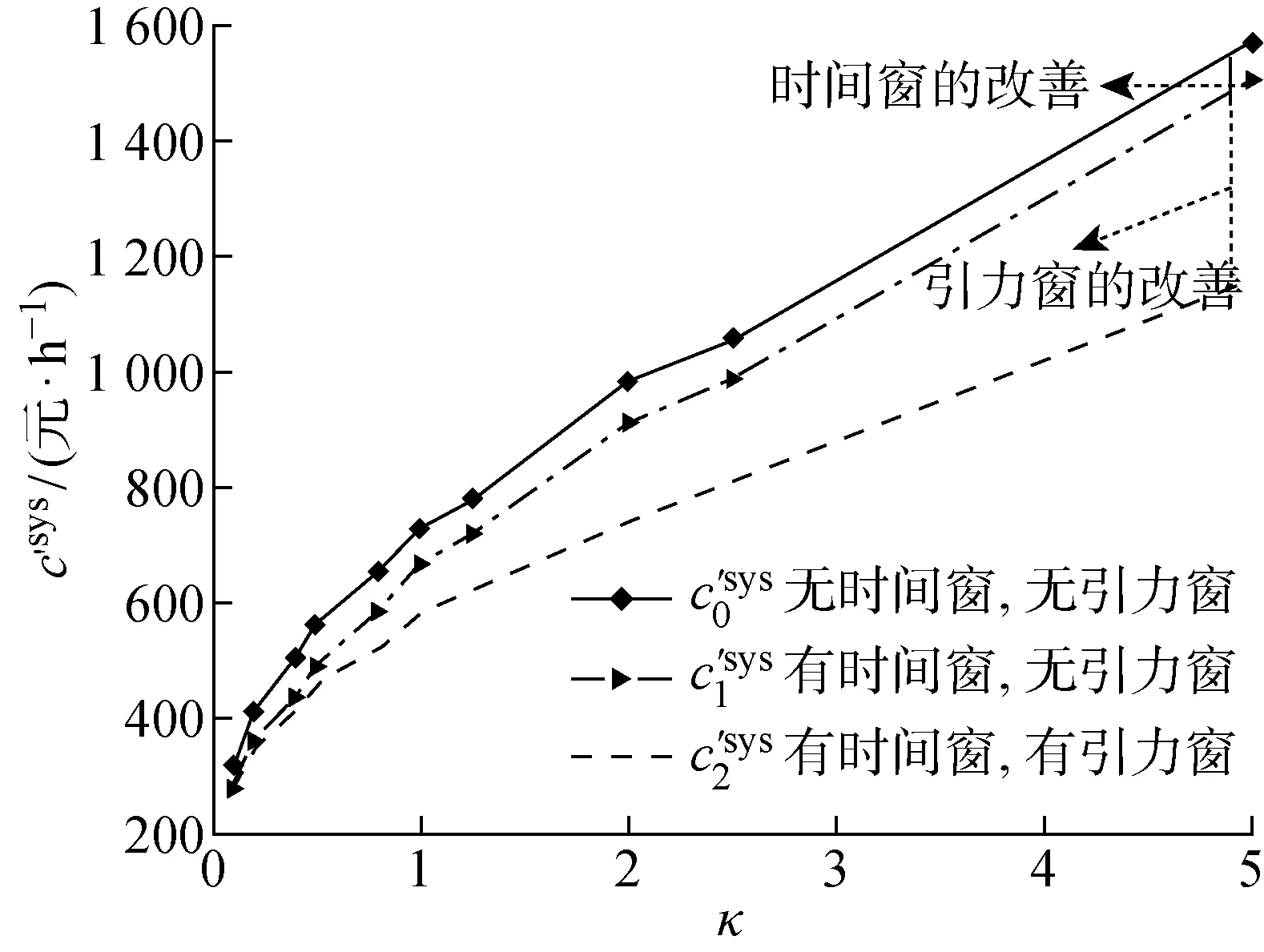
圖5 不同停機成本下的系統維護總成本率分析Fig.5 Total cost rate analysis of system maintenances at different downtime costs

(34)

隨著停機成本的增加，φ的變化如圖6所示.由圖6可知，停機成本越大，φ越大，意味著引力窗改進的效果越明顯.這是因為當停機成本增加時，設備更趨向于利用生產等待進行機會維護，從而避免設備強制性預防維護導致巨額停機成本的情況.由仿真結果可知，當κ=0.1時，最優維護策略下，在維護規劃期內由外部機會引發的系統維護的平均次數為10.152 5次，由內部機會引發的系統維護的平均次數為6.928次；而當κ=50時，最優維護策略下，由外部機會引發的系統維護的平均次數為7.826次，由內部機會引發的系統維護的平均次數僅為0.015次.故停機成本越大時，引力窗對于系統維護計劃的改進越為重要；停機成本相對較小時，時間窗對于系統維護計劃的改進越為重要.不同停機成本下的具體仿真及優化結果如表3所示.

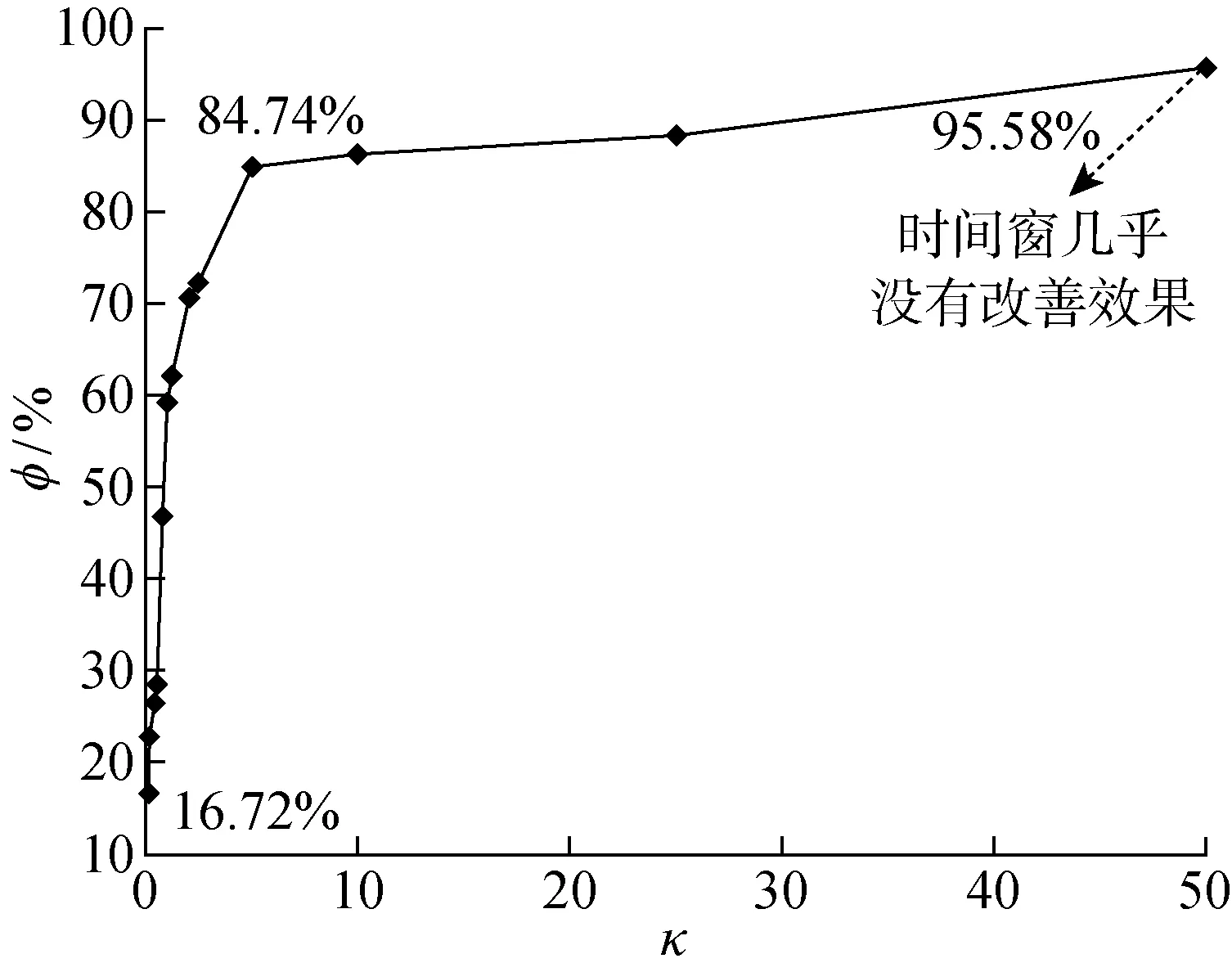
圖6 不同停機成本下的引力窗改善占比分析Fig.6 Analysis of the proportion of gravity window improvements at different downtime costs

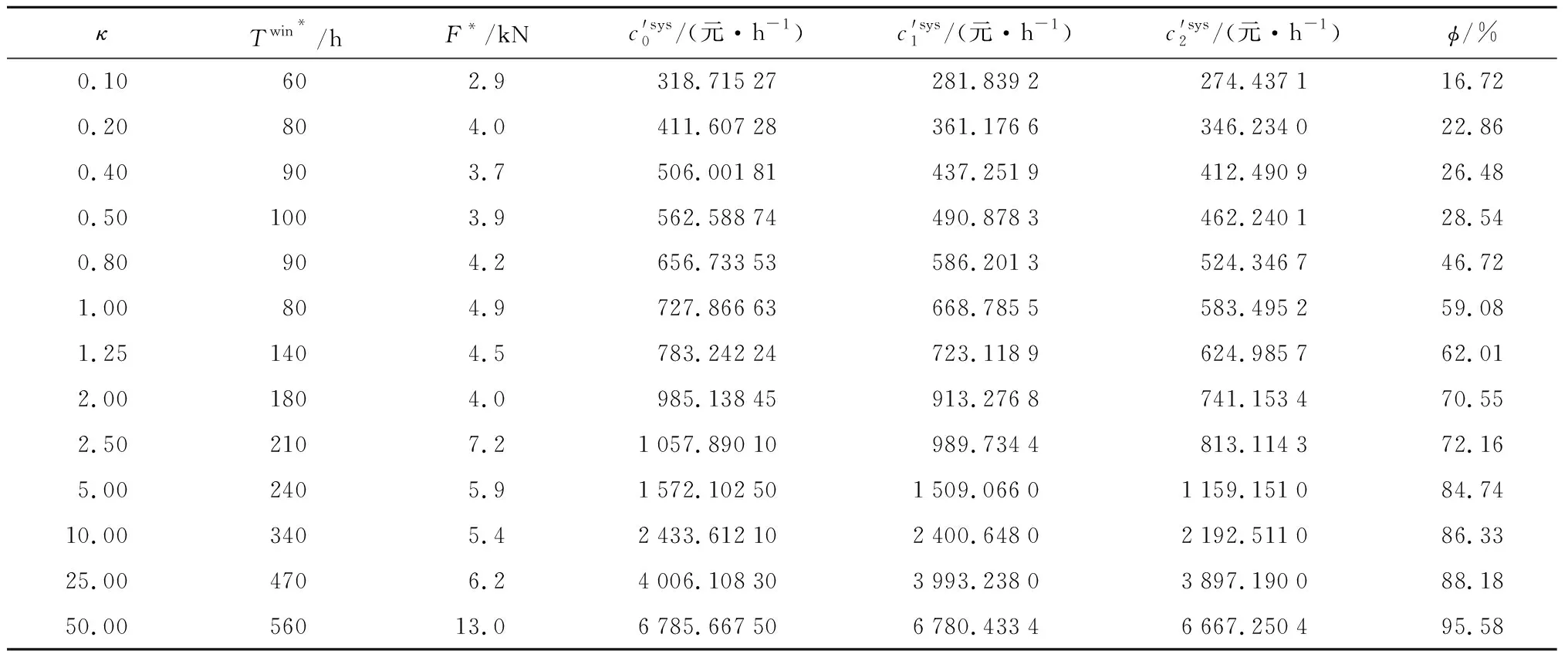
表3 不同停機成本的仿真結果Tab.3 Simulation results of different downtime costs

3.3 不同生產等待到達頻率的策略對比

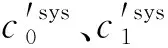
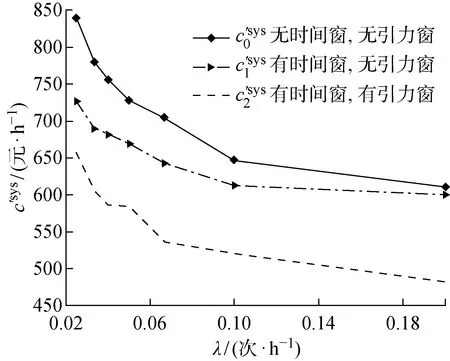
圖7 不同生產等待到達頻率下的系統維護總成本率分析Fig.7 Total cost rate analysis of system maintenances at different production wait frequencies

此外，隨著λ的增大，φ的變化如圖8所示.由圖8可知，λ越大，φ越大，意味著生產等待的到達越頻繁，引力窗改進的效果越明顯.這是因為生產等待的到達越頻繁，設備越大概率地利用生產等待進行機會維護.由仿真結果可知，當λ=0.025 次/h時，在維護規劃期內由外部機會引發的系統維護的平均次數為7.462次，由內部機會引發的系統維護的平均次數為 1.730 5 次；而當λ=0.2 次/h時，由外部機會引發的系統維護的平均次數為14.082次，由內部機會引發的系統維護的平均次數僅為 0.045 5 次.故生產等待的到達越頻繁，引力窗對于系統維護總成本率的改進越為重要；生產等待到達相對稀疏時，時間窗對于系統維護總成本率的改進越為重要.不同生產等待到達的頻率下的具體仿真及優化結果如表4所示.

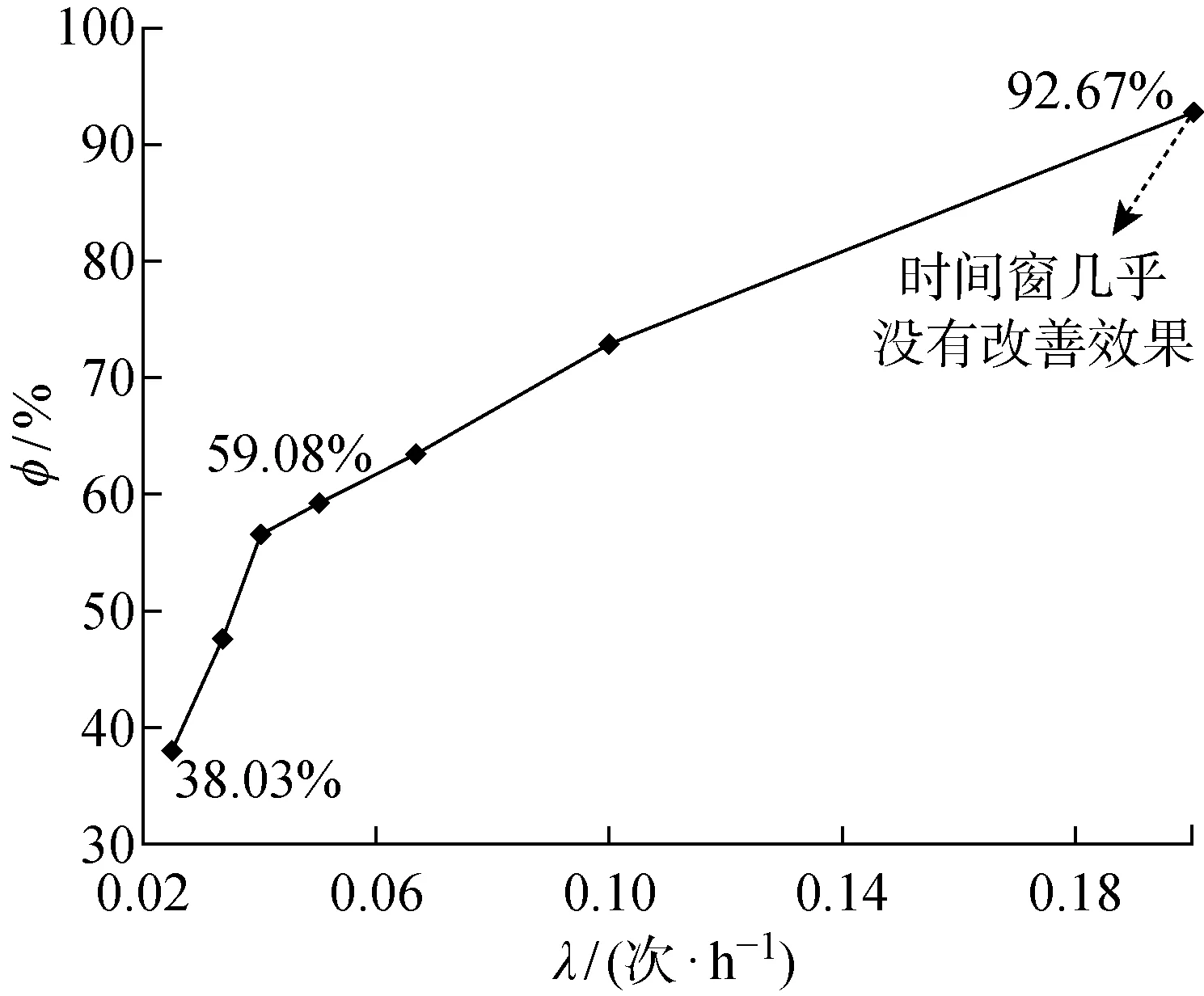
圖8 不同生產等待到達頻率下的引力窗改善占比分析Fig.8 Analysis of the proportion of gravity window improvements at different production wait frequencies

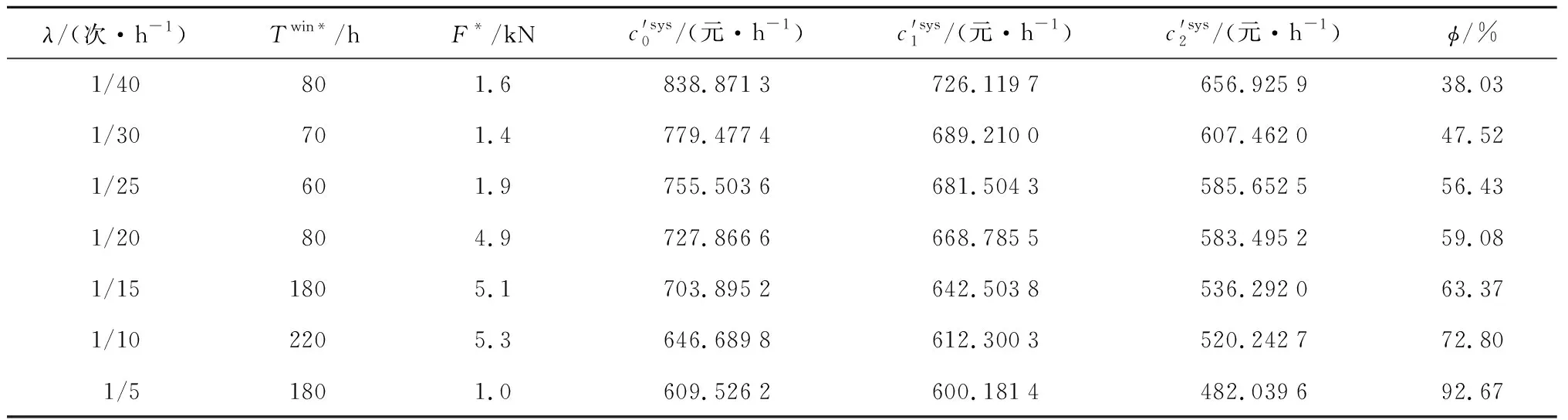
表4 不同生產等待到達頻率的仿真結果Tab.4 Simulation results of different production wait frequencies

4 結語

本文同時考慮了串行生產系統面臨的由預防維護引發的內部維護機會以及由生產等待帶來的隨機外部維護機會，提出時間窗與引力窗相結合的機會維護策略.對設備和系統分別進行維護建模，利用時間窗對內部機會引發的維護活動進行整合，利用引力窗對外部機會引發的維護活動進行整合.算例分析結果表明，在復雜的參數環境中，相對于無維護整合模型和時間窗模型，時間窗與引力窗相結合的決策模型均可以獲得更低的系統維護總成本率，具有廣泛的適應性與穩定性，且隨著停機成本的增大或生產等待到達頻率的提高，引力窗的改善占比呈遞增趨勢.因此，在停機成本較高或生產中斷頻繁發生的串行生產系統中，引力窗對于維護計劃的改進更為重要.