考慮延遲的汽車線控轉向系統自適應內模控制

劉文通, 陳 俐, 陳 峻

(上海交通大學 動力裝置及自動化研究所；海洋工程國家重點實驗室，上海 200240)

線控轉向利用電子線路取代從方向盤到轉向執行器之間的機械連接，具有結構緊湊、布置方案靈活且更易于實現集成控制等優點，是自動駕駛汽車實現路徑跟蹤與避障避險的關鍵技術之一[1-2].但是，由于信號傳輸、轉向執行機構中機械間隙、摩擦等原因，線控轉向系統存在響應延遲.延遲使得控制系統的調節時間變長、超調量增大，嚴重時甚至能引起振蕩或失穩[3].此外，延遲時間會隨著不同系統的結構、老化程度和通信負荷等發生變化.為了改善線控轉向系統的動態性能，有必要設計對延遲具有自適應補償效果的控制策略.

近年來，線控轉向系統中的延遲問題逐漸引起關注.文獻[4]的研究表明，當網絡傳輸延遲大于一個通信周期的概率超過10%時，將引起線控轉向系統功能失效.文獻[5-6]發現當延遲大于50 ms時，采用比例微分控制的線控轉向系統會發生失穩.為了消除延遲對線控轉向系統轉角跟蹤性能的影響，文獻[6]針對轉向執行系統的固定延遲，提出基于 Lyapunov漸近穩定性判定方法確定轉角跟蹤的反饋增益.文獻[7]針對方向盤與轉向執行系統之間的不確定有界信號的傳輸延遲，設計模糊反饋增益，以保證系統的漸近穩定性.這些方法局限于固定或有界延遲，不適用于時變、界限未知的線控轉向系統的高精度轉角跟蹤.

內模控制(IMC)具有對偶穩定性、理想控制器特性和零穩態偏差特性[8]，對模型誤差具有一定的穩健性和較強的抗干擾能力[9]，內模控制能較好地減弱延遲的影響[10].自適應內模控制(AIMC)可隨著系統參數時變而自動調整增益，提高跟蹤精度[11].然而，延遲是非線性環節，給自適應內模控制的實施帶來了困難.一方面，難以對延遲進行高精度辨識，比如近年來基于模型的最小二乘法[12]和梯度下降法[13]，以及模型無關的階躍響應法[14]和相關分析法[15]等研究采用較復雜的算法試圖提高辨識精度；另一方面，內模控制的逆控制器需要對被控對象的名義模型求逆，并據此設計濾波器，延遲環節為逆控制器和濾波器的設計帶來諸多不便.因此，一些研究在逆控制器求解時不得不將延遲環節摒棄.文獻[16]采用的最速下降法、文獻[17]采用的人工神經網絡來辨識時變延遲，雖然獲得了含延遲的名義模型，但是延遲環節信息并未用于逆控制器的設計，故未能嚴格實現內模控制理想控制器特性和零穩態偏差特性.

對延遲環節進行線性近似，可以克服非線性環節導致的內模控制的設計障礙.文獻[18]采用的Pade近似、文獻[19]采用的Taylor近似都是將延遲環節線性化后，再設計增益自調整的自適應控制律.但是，這些研究尚存在兩個缺陷，一是Pade和Taylor近似均產生右半平面零點，引入非最小相位部分，這部分在設計內模控制的逆控制器時往往也被摒棄；二是線性近似表達式的系數取定值未能反映時變延遲的特性，限制了跟蹤精度的提高.全極點近似方法將延遲環節分母進行Taylor展開，可避免產生右半平面零點，不會出現非最小相位部分[20]，可直接用于逆控制器的設計.迄今，全極點近似尚未用于內模控制器的設計.Kalman濾波算法簡單、高效且易于實現，被廣泛應用于各種有噪聲的參數估計問題[21].

本文首先建立線控轉向系統的轉向執行機構動力學模型與延遲環節模型，然后設計自適應內模控制框架中的線性近似名義模型、逆控制器和Kalman濾波辨識算法;提出采用全極點近似方法近似延遲環節，將線性近似延遲模型與線控轉向系統模型相結合，為被控對象構建新的含有延遲項的名義模型；引入Kalman濾波方法辨識名義模型參數，據此設計自適應內模控制律，從而適應時變延遲對控制性能的影響，與采用線性近似模型的自適應內模控制相結合，既降低算法的復雜度，又可提高具有時變延遲的線控轉向系統的轉角跟蹤精度.MATLAB/Simulink仿真給出不同延遲作用下線控轉向系統的轉角跟蹤性能，與逆控制器未計入延遲的傳統內模控制，比例、積分、微分(PID)控制分別進行比較.最后，開展臺架試驗，并比較這3種方法的跟蹤性能.本文為含有延遲的線控轉向等遙操作系統的控制提供了理論依據.

1 線控轉向系統建模

在線控轉向系統中，轉向執行系統接收線控轉向系統控制器發出的扭矩指令并執行.從控制器發出扭矩指令到轉向執行系統開始執行該扭矩指令之間存在延遲.延遲主要源于3個因素，其一為通信延遲，其二為轉向執行系統間隙、摩擦相關的機械延遲，其三為傳感器信號的采集與處理延遲.這些因素對線控轉向系統的影響可以歸結為對扭矩指令的響應延遲.因此，本節建模分為轉向執行系統模型和延遲環節模型，二者串聯組成被控對象模型.

1.1 轉向執行系統模型

前輪轉向執行系統主要由轉向執行電機和齒輪齒條轉向器組成，如圖1所示.其中：xr為轉向器齒條的位移；Mm為轉向電機輸出力矩.

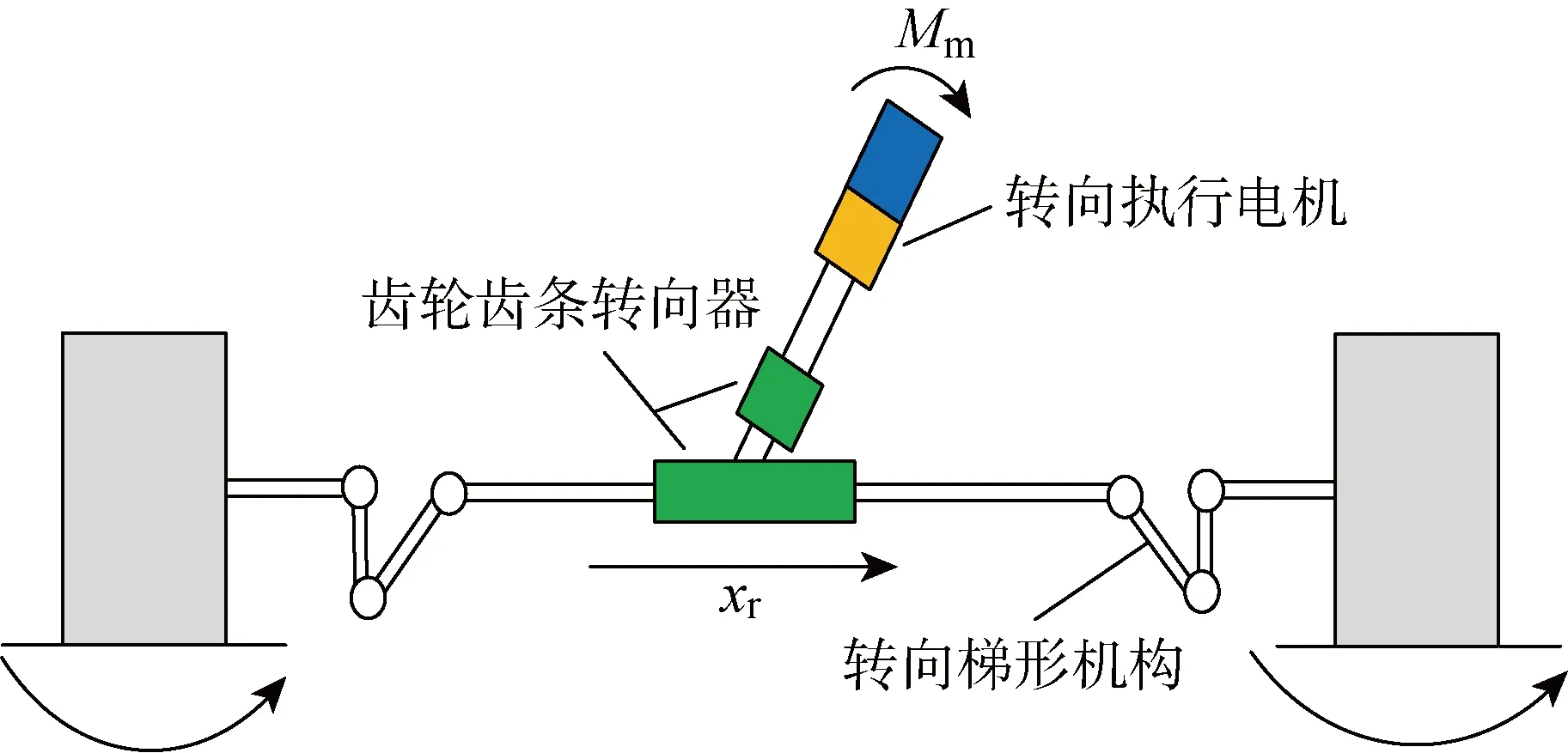
圖1 轉向執行系統物理模型Fig.1 Physical model of steering execution system

轉向執行系統的動力學方程如下[22]：

(1)

式中：mr為齒輪齒條轉向器的質量；Cr為轉向器齒條的阻尼系數；gm為轉向電機的減速比；rp為轉向小齒輪的分度圓半徑；Fr為左右前輪施加齒條上的轉向阻力；δf為前輪轉角；K為梯形轉向機構前輪轉角到齒條位移的比例系數.

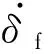
(2)

式中：a11、a12為阻力系數.

定義轉向執行系統的控制輸入u=Mm，輸出y=δf，對式(1)和(2)進行拉氏變換，經推導可得從輸入u(s)到輸出y(s)的傳遞函數為

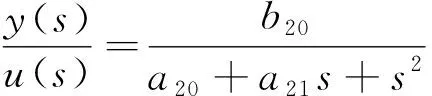
(3)

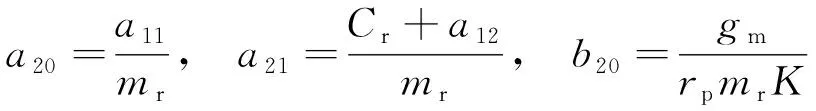
(4)

式中：s為微分算子.

1.2 延遲環節模型

延遲τ使得轉向電機扭矩被延遲執行.令轉向電機扭矩指令為Mmc，式(1)中的轉向電機扭矩Mm由下式表示：

Mm(t)=Mmc(t-τ)

(5)

式中：t為時間.

延遲環節的傳遞函數為

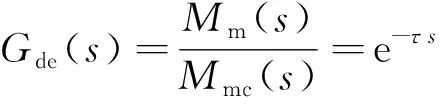
(6)

應用一階全極點近似方法[20]對式(6)進行近似可得：

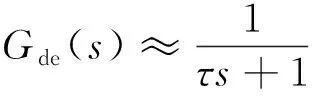
(7)

1.3 線控轉向系統模型

將延遲環節模型(見式(6))與線控轉向執行系統模型(見式(3))串聯，獲得考慮延遲的被控對象系統的傳遞函數如下，其中a20、a21、b20為被控對象的模型參數.

(8)

2 自適應內模控制器

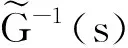
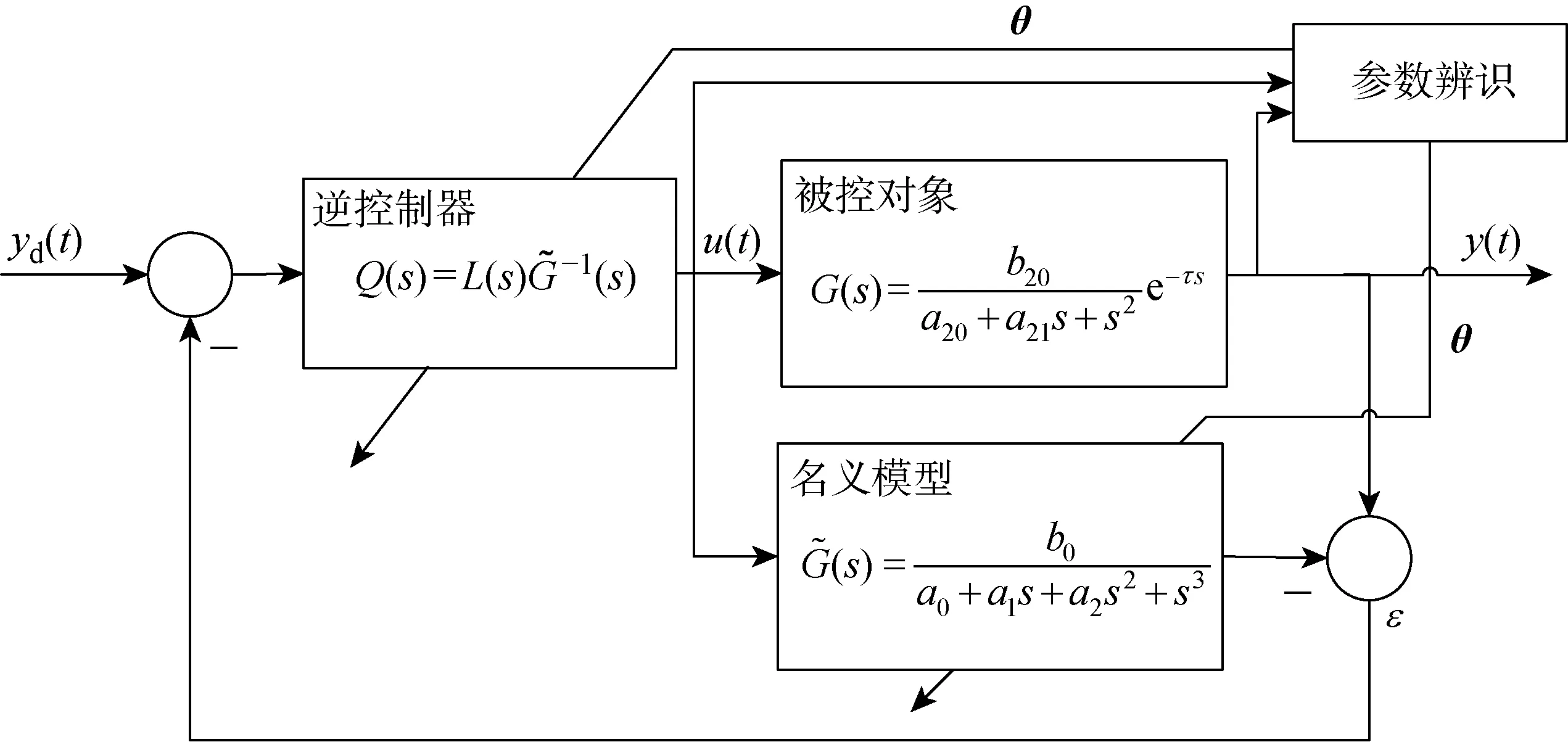
圖2 自適應內模控制框圖Fig.2 Block diagram of adaptive internal model control

2.1 名義模型

將式(7)代入式(8)，可得含延遲的線控轉向系統線性近似名義模型為

(9)

(10)

該模型具有線性系統的表達形式，便于逆控制器中的求逆運算，可見延遲τ能夠改變傳遞函數的系數.

2.2 逆控制器

逆控制器Q(s)按如下設計：

(11)

(12)

低通濾波器L(s)按如下設計：

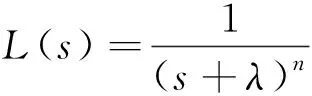
(13)

式中：λ為濾波器時間常數，用于調節跟蹤控制性能；n為正整數，用于補償逆控制器Q(s)的相對階，使逆控制器可實現.

2.3 參數辨識

式(9)的線性近似模型可表達如下：

z=φTθ

(14)

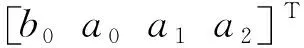
(15)

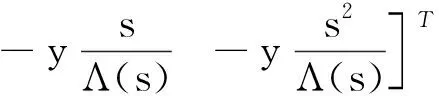
(16)

式中：Λ(s)=(s+λ1)3為Hurwitz多項式，λ1為參數辨識濾波器常數；1/Λ(s)是為了避免在參數辨識中出現求導而引入的濾波器[25].

令采樣周期為Δt，在第k個采樣時刻，參數θ(k)的離散狀態空間表達式為

(17)

(18)

式中：w(k)為過程噪聲，e(k)為測量噪聲，二者均假設為高斯白噪聲；R1為w(k)的協方差矩陣；R2為e(k)的協方差；E為數學期望.

在第k個采樣時刻，Kalman濾波算法的迭代式可表示為

(19)

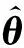
3 仿真結果

在MATLAB/Simulink軟件中進行仿真，參數如表1所示.其中：P0為初始參數協方差矩陣；Δt為采樣周期.本文提出的AIMC與傳統IMC以及PID控制的結果相比較，傳統IMC方法中名義模型含延遲環節，但在逆控制器設計中未對延遲環節求逆，傳統PID方法針對含延遲的被控對象實施PID反饋控制.3種控制策略中，被控對象的參數一致，都來自由臺架試驗獲得的輸入輸出數據并進行離線參數辨識獲得.傳統PID控制的比例、積分、微分增益分別為0.1、0.2、0.01.

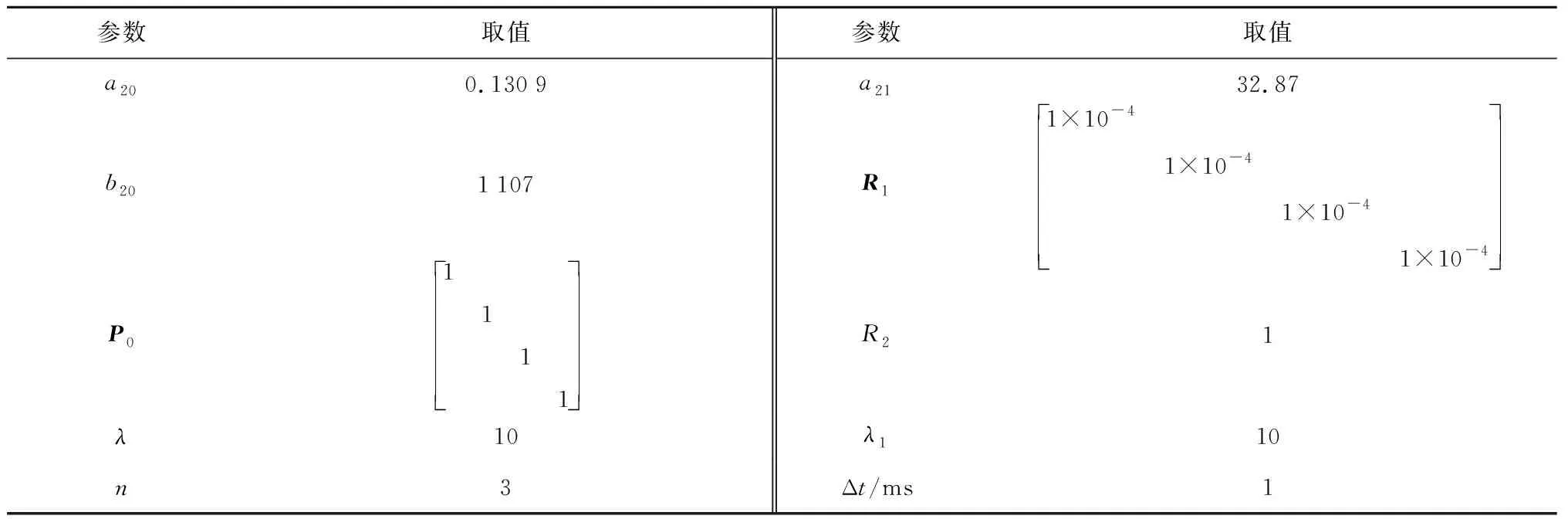
表1 仿真參數設置Tab.1 Parameters of simulation setting

以幅值為10、周期為10 s的方波模擬左右反復轉向作為參考輸入，考慮實際傳感器測量值存在噪聲，在系統輸出中加入信噪比為3%的白噪聲.τ=50、100 ms的仿真結果分別如圖3和4所示，其中Ref為參考信號.每組圖給出了轉向執行電機力矩、名義模型與被控對象輸出的誤差(即模型誤差)、轉向角歷程、轉向角跟蹤誤差以及在線辨識的參數值.對線控轉向控制系統的轉角跟蹤性能，從轉向執行時間、跟蹤穩定時間以及跟蹤超調角度3個方面對轉向角跟蹤控制進行評價.仿真結果的評價指標如表2所示.其中：t1為轉向執行時間，指實際轉角從開始變化到第一次達到目標轉角的時間；t2為跟蹤穩定時間，指實際轉角從開始變化到不超過終值2%的時間；ω為跟蹤超調角度，指實際轉角超過目標角度的最大值.

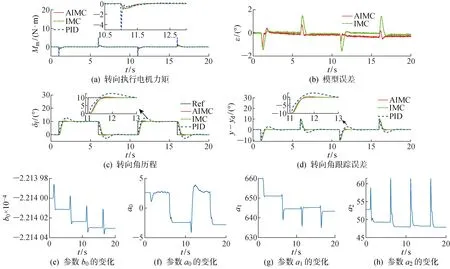
圖3 τ=50 ms時的仿真結果Fig.3 Simulation results at τ=50 ms

由表2和圖3(d)可知，當τ=50 ms時， AIMC的轉向執行時間最長為0.85 s，而IMC與PID控制的轉向執行時間分別為0.58、0.48 s.但AIMC的穩定時間最短，僅為1.06 s， 而IMC與PID控制的穩定時間分別為1.33、3.63 s.此外，AIMC的跟蹤超調角度最小，僅為0°，而IMC與PID控制的跟蹤超調角度分別為0.535°和2.694°.AIMC的控制性能較好得益于其模型誤差較小(見圖3(b))，AIMC的名義模型與被控對象輸出的誤差明顯小于IMC.在AIMC的設計中有兩點為減少模型誤差做出了貢獻，其一是名義模型中考慮了延遲環節，其二是系統模型的參數通過在線辨識獲得.參數辨識的結果如圖3(e)～3(h)所示.參考轉角發生階躍變化引起系統響應的瞬時變化，進而導致參數辨識的結果也發生相應的變化，但每次階躍之后的參數辨識都能快速收斂，使AIMC獲得良好的系統性能.傳統IMC雖然對模型誤差具有穩健性，但由于其名義模型存在誤差，模型誤差較大使得跟蹤誤差也較大.傳統PID控制采用固定增益，為了盡快跟蹤階躍信號，PID控制的轉向執行電機力矩最大(見圖3(a))，其轉向執行時間最短，但也因此引起了較大的超調角和震蕩，進而導致穩定時間有所延長.

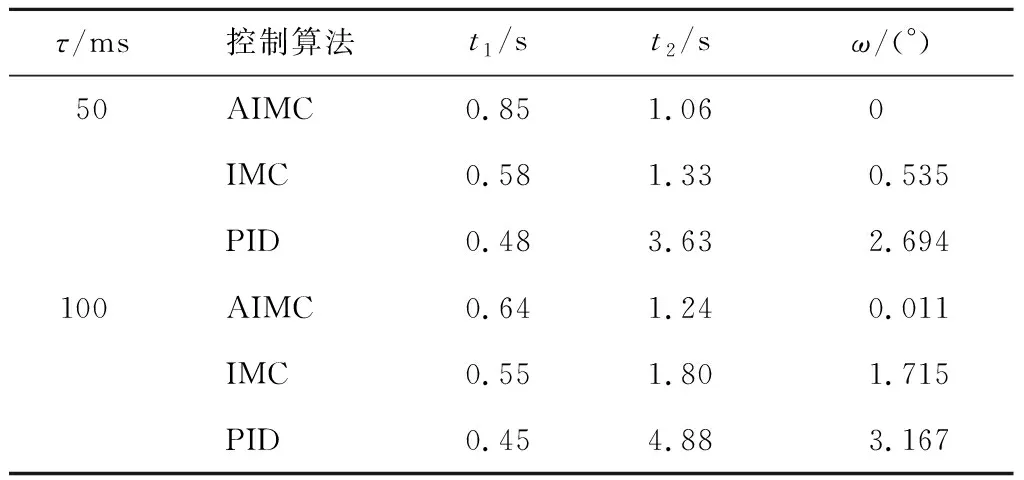
表2 仿真結果Tab.2 Simulation results

由圖4(d)和表2可知，當τ=100 ms時，與τ=50 ms時相比，AIMC的轉向執行時間略縮短為0.64 s，跟蹤穩定時間為1.24 s，略有所延長.跟蹤超調角度雖然增大到了0.011°，但都遠小于其他兩種控制器的結果.由此可見，即使延遲時間增大為2倍，轉向角跟蹤控制的性能基本保持不變，體現了AIMC對延遲變化的自適應能力.相較于傳統IMC和PID控制，與τ=50 ms時的情況類似，AIMC的轉向執行時間最長，IMC為0.55 s，PID控制為0.45 s；但是AIMC的穩定時間最短，IMC為1.8 s，PID控制為4.88 s.此外，AIMC的跟蹤超調角度最小，IMC為1.715°，PID控制為3.167°.綜上所述，與τ=50 ms時的情況相比，傳統IMC和傳統PID控制的性能指標發生了較大變化，反映了對延遲變化的適應能力不足.

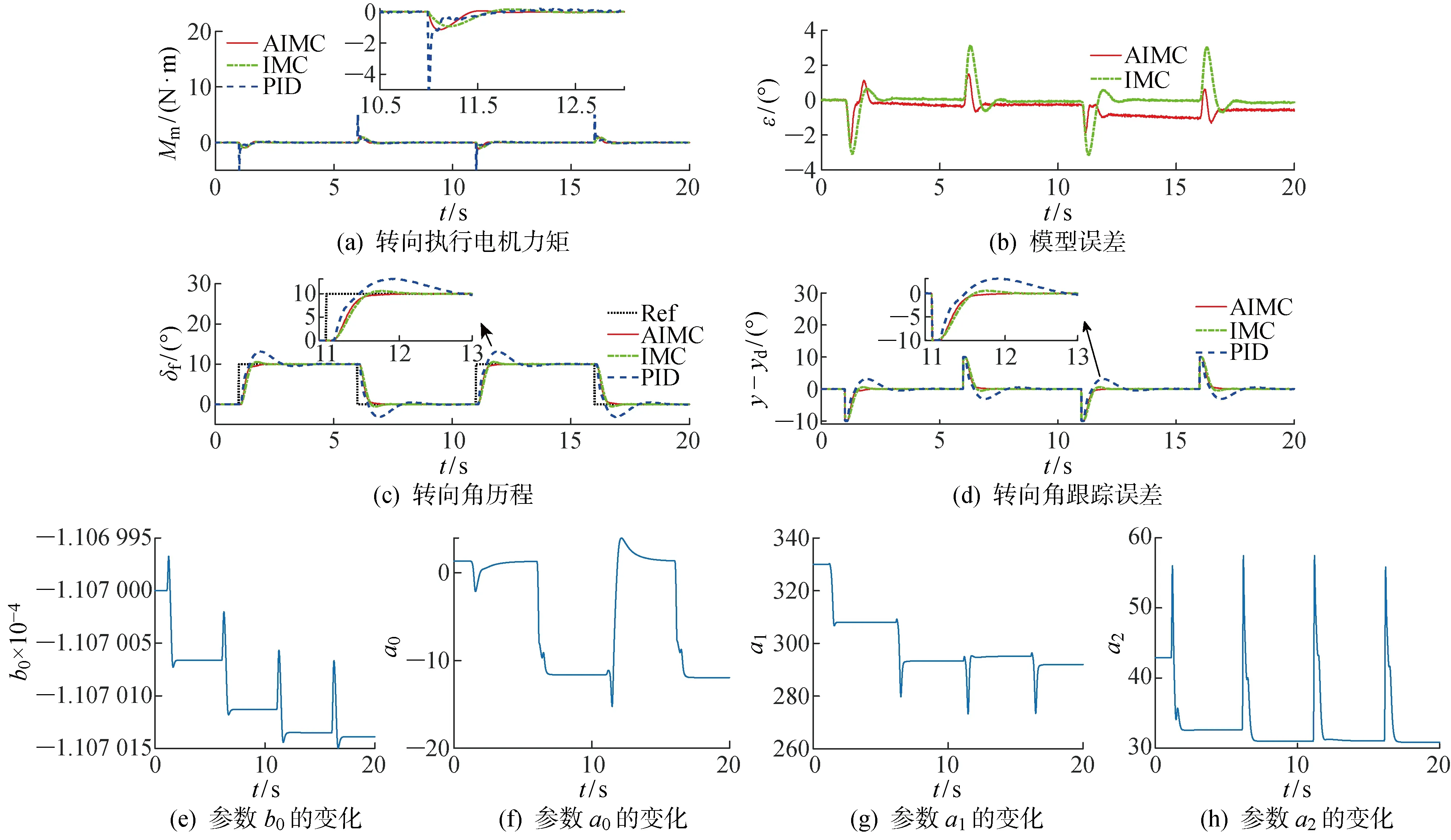
圖4 τ=100 ms時的仿真結果Fig.4 Simulation results at τ=100 ms

4 臺架試驗結果

基于快速控制原型設備建立線控轉向試驗平臺，如圖5所示.試驗平臺由某國產乘用車型實車前橋轉型機構、dSPACE MicroAUTOBOX快速控制原型設備、轉向執行電機、電機控制器、dSPACE ControlDesk開發主機、位移傳感器、電源等組成.直流穩壓電源給電機驅動提供13.5 V電源，為傳感器提供5 V電源.位移傳感器測量轉向機構齒條的位移，可根據式(1)轉換成前輪轉角.本文提出的控制策略首先在MATLAB/Simulink中實現，然后由dSPACE ControlDesk軟件編譯并下載至dSPACE MicroAUTOBOX快速控制原型，采集位移傳感器信息，并通過控制器局域網絡(CAN)總線將轉向電機輸出力矩指令發給電機控制器， CAN的發送周期為10 ms.

圖5 線控轉向試驗臺架Fig.5 Steer-by-wire test bench

試驗中，延遲主要有3個來源，通信延遲、機械延遲和數據采集與處理延遲.其中，機械延遲反映在轉向系統的被控對象模型中，參數可通過離線辨識獲得.被控對象模型參數與仿真匹配如表1所示，但是受溫度、濕度、使用壽命等影響，被控對象模型參數會發生一定程度的變化.數據采集與處理延遲會隨著采集硬件和處理算法而變化.通信延遲與通信周期和網絡負荷有關，后兩者可以通過給τ賦值進行模擬.首先，未施加額外延遲，即τ= 0 ms，試驗結果如圖6所示.然后，額外施加100 ms延遲，即τ=100 ms，試驗結果如圖7所示.所提AIMC和傳統IMC、傳統PID控制的對比結果如圖6和7所示.試驗中的控制性能指標如表3所示.

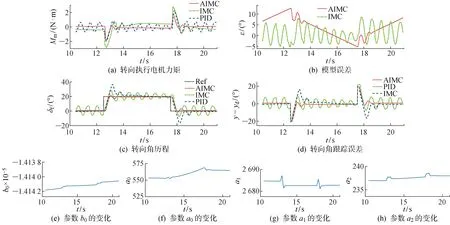
圖7 τ=100 ms時的臺架試驗結果Fig.7 Bench test results at τ=100 ms

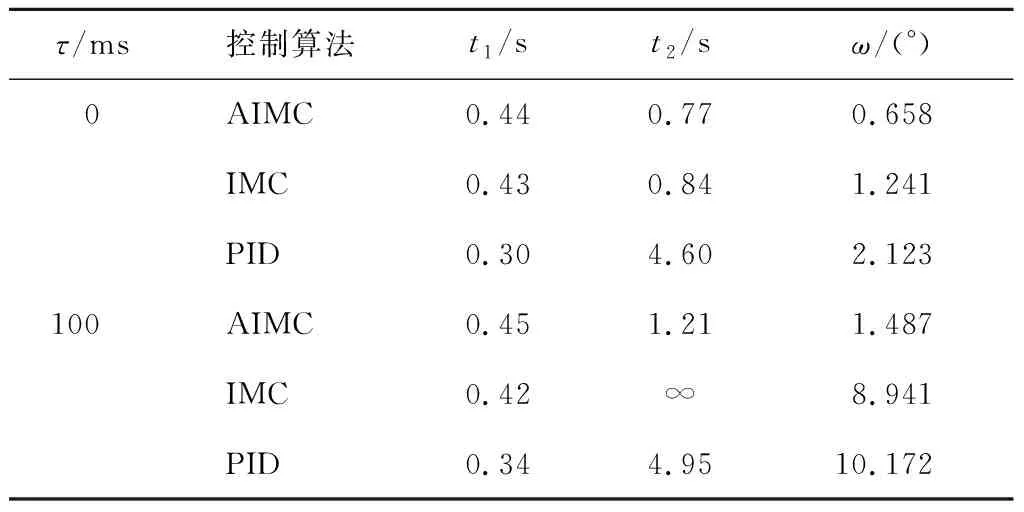
表3 試驗結果Tab.3 Test results

由圖6(a)可知，當沒有額外施加延遲時，AIMC的轉向執行電機力矩均小于傳統IMC和PID控制的轉向執行電機力.由圖6(d)可知，AIMC的轉向執行時間最長為 0.44 s，而傳統IMC和PID控制的轉向執行時間分別為 0.43 s 和 0.30 s；AIMC的穩定時間最短為 0.77 s，而傳統IMC和PID控制的穩定時間分別為 0.84 s 和 4.60 s.此外，AIMC的跟蹤超調角度最小為0.658°，而傳統IMC和PID控制的跟蹤超調角度分別為1.241° 和2.123°.因此，AIMC利用較小的轉向執行電機力矩獲得了比傳統IMC和PID控制更高的跟蹤精度.

圖6 τ=0 ms時的臺架試驗結果Fig.6 Bench test results at τ=0 ms

由圖7(c)可知，當額外施加100 ms延遲時，AIMC和PID控制都能實現跟蹤，但傳統IMC發生了震蕩甚至發散.比較圖7(d)和圖6(d)可知，受額外延遲增大的影響，AIMC轉向延遲時間為0.45 s，有微小增加，穩定時間為1.21 s也有所增加；跟蹤超調角度為1.487°，增大了1倍.同時，傳統IMC和PID控制受到更明顯的影響，傳統IMC無法實現穩定，超調角達到8.941°，增長了約12倍；PID控制的超調角度達到10.172°，增長了約5倍.試驗結果表明，AIMC對實際變化后的不同延遲具有適應性，跟蹤性能優于傳統IMC和PID控制.

5 結語

本文在考慮線控轉向系統中存在未知、時變延遲的情況下，提出采用全極點近似方法，將線性近似的延遲環節與線控轉向系統模型相結合，為被控對象構建新的線性近似名義模型.引入Kalman濾波方法實時辨識名義模型參數，并據此設計自適應內模控制律.不同延遲時間下的仿真、臺架試驗結果均表明，所提自適應內模控制比傳統內模控制和PID控制的跟蹤精度高、穩定時間短，且對不同延遲的適應能力強.