基于壓縮感知的MIMO-OFDM系統自適應信道估計*

李姣軍，蔣 揚，邱 天，左 迅，楊 凡

(重慶理工大學 電氣與電子工程學院，重慶400054)

0 引 言

將多輸入多輸出(Multiple-Input Multiple-Output,MIMO)與頻譜利用率高、抗多徑干擾的正交頻分復用(Orthogonal Frequency Division Multiplexing,OFDM)結合[1]可有效提高頻譜利用率。隨著天線數量的不斷增長，熱噪聲對系統的影響變得微乎其微，發送給目標用戶的信息對其他用戶的干擾趨于消失[2-4]。為獲取這些增益，基站(Base Station,BS)側需要對發射的下行鏈路信道的傳輸信號做預編碼處理，這就需要BS預先獲得下行鏈路的信道狀態信息。下行鏈路的信道信息獲取越精確，做預編碼得到的效果就越好，越能有效克服干擾和失真。為減少信道估計中導頻使用開銷，多數研究集中在時分雙工模式下，利用上下行鏈路互易性避免導頻開銷偏大。然而，上下行鏈路的互易性并不嚴格成立，需要復雜的校準，且相干時間有限，依據互易性獲得的下行鏈路信道狀態信息(Channel State Information,CSI)準確度可能不高，難以滿足基站側預編碼的要求[5]。為達到5G中對于用戶體驗速率的要求，超密集組網的趨勢不可阻擋，為此不可避免在相鄰小區使用非正交導頻，其帶來的干擾將嚴重影響信道估計準確性，限制MIMO-OFDM系統的性能，因此利用短導頻進行下行鏈路信道估計成為當今的研究熱點[6-8]。

在寬帶通信系統中，信道多呈現稀疏性[9]，即信道具有很大的時延擴展，但其能量集中在少數路徑上，其他路徑能量很小。由于信道所具有的特性，故可以利用壓縮感知技術，通過少量觀測值得到良好的信道估計性能，且較于傳統算法復雜度更低[10]。貪婪算法是壓縮感知重建算法中一類常用算法，相較于凸優化方法，具有更低的復雜度，故而使用的更加廣泛。正交匹配追蹤(Orthogonal Matching Pursuit，OMP)作為貪婪算法的代表算法，常用于對稀疏信道進行估計，但其在稀疏度較大時迭代時間長[11]。為減少算法迭代次數，文獻[12]提出了一種變步長分段自適應匹配追蹤(Variable Step Size Stagewise Adaptive Matching Pursuit，VSStAMP) 算法，以索引集原子個數來做階段標識，在不同階段使用變步長來擴展支撐集，以較快速度逼近真實稀疏度，但在稀疏度偏大時仍需較長的迭代時間。

針對上述問題，本文提出了一種冪函數稀疏度自適應匹配追蹤(Power Sparsity Adaptive Matching Pursuit,PSAMP)算法，該算法由稀疏度預估計和追蹤重構兩部分構成。與傳統信道估計算法相比，所提算法增加了冪函數試探進行預估計，減少了后續迭代次數，并引入回溯機制，保證了良好的信道估計性能。

1 系統模型

1.1 壓縮感知基本理論

許多自然界的信號x∈N是可以被壓縮的，即它們可以用稀疏信號表達出來，通常做法是將其在合適的域進行投影，這意味著x可以由N組基向量ψi(i=1,2,…,N)構成正交基字典ψ=[ψ1,ψ2,…,ψN]表示：

x=ψθ。

(1)

此時，若θ最多有K(K?N)個非零元素，那么可以稱信號x在ψ域的投影是具有K稀疏特性的。若設計一個觀測矩陣Φ∈M×N，其與正交基字典相關性為零或最大限度小，用以觀測信號x，則可以得到測量值y∈M，用公式表達即

y=Φx。

(2)

又由式(1)可得

y=Φx=Φψθ=ACSθ。

(3)

式中：ACS為一個M×N維的矩陣，稱為感知矩陣。在已知y和ACS的前提下，可以利用l0范數意義下優化求解上述問題：

(4)

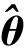
(1-δK)‖x‖2≤‖Φx‖2≤(1+δK)‖x‖2。

(5)

式中：參數δK∈(0,1)。式(4)的優化方程的求解是一個NP-hard問題，求解此類問題存在困難，需要做相應調整。文獻[10]的研究表明，當觀測矩陣Φ具有參數的δK∈(0,1)的RIP性質時，組合優化問題可以轉換成求解最小化l1范數問題，兩者可以得到同樣的解。

(6)

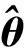
1.2 MIMO-OFDM系統

考慮一個MIMO-OFDM系統，基站側配置有Nt根天線，接收端天線配有Nr根，使用K個子載波，其結構框架如圖1所示。

圖1 MIMO-OFDM系統模型

假設系統傳輸模型為慢衰落頻率選擇性衰落信道，則可以看作在一個符號間隙內信道參數幾乎不變。設插入導頻數量為M，分別放置在k1,k2，…,kM上，則在接收端第j根天線上收到的導頻為

(7)

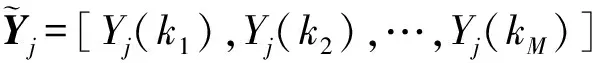
(8)

則式(7)可以改寫為

(9)

Yj=Φhj+Nj，

(10)

進一步寫成

Y=Φh+N。

(11)

由于信道沖激響應h具有稀疏性，故可以應用壓縮感知技術，利用接收信號Y和Φ重構出h。根據估計出的h，可以計算出發射端預編碼的矩陣W。為方便得到預編碼矩陣，令

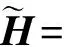
[H11,…,H1Nt,H21,…,HNr Nt]，

則式(11)可以改寫成

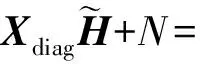
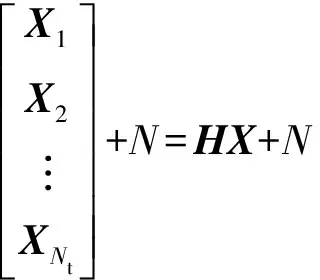
(12)

在采用迫零預編碼的情況下，相應的加權矩陣可以表示成

W=H-1。

(13)

2 壓縮感知重構算法

憑借壓縮感知技術，可以在使用少量導頻的情況下完成對稀疏信道h的估計，估計性能的好壞取決于導頻放置方式和壓縮感知重構算法的設計。本節主要考慮壓縮感知重構算法的設計，分為稀疏度預估計和追蹤重構兩部分，其中導頻位置放置方式為隨機。首先給出算法的第一部分稀疏度預估方法，其思想是通過不斷擴大支撐集進行匹配測試，獲得的支撐集的勢略小于原始信號真實稀疏度。

2.1 冪函數試探思路

由文獻[13]可以給出下面預估計理論的命題：

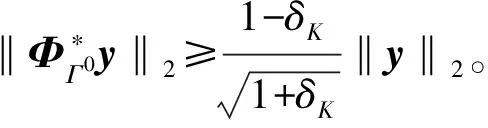
由于上述結論是充分不必要的，因此實際使用時，通常使用其結論的逆否命題來判斷對稀疏度的預估計值是否過估計。

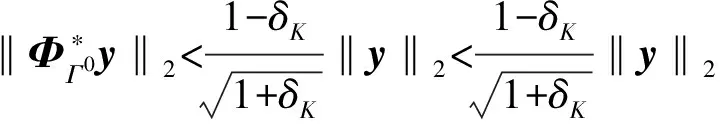
由上述定理可以得到對稀疏度進行預估的方法：首先對K0取1，逐漸增加K0的值，直至上述不等式不成立為止。這樣計算相較于傳統算法可以快速得到一個稀疏度預估計值，但是逐次增加也會降低算法效率。本文引入分段思想，首先以冪函數進行試探，令步長自適應試探次數變化，這樣設計可以快速逼近真實稀疏度。冪函數的基本形式如下所示：

Ki+1=Ki+「ib?×s。

(14)

式中：i=1,2,…,n為階段試探次數；起始步長為s；b為控制搜索步長參數，通常設置為0.5～0.7，這樣設計能在保證精度的同時以較快的速度擴大支撐集來逼近信號真實稀疏度，從而得到一個粗略估計稀疏度值，再通過小步長逐漸逼近得到準確的稀疏度估計值。

2.2 算法步驟

算法的流程圖如圖2 所示。

圖2 算法流程圖

整體算法步驟如下：

輸入：感知矩陣A=XPWP，接收到的導頻信號yP，標識閾值參數μ，原子篩選參數α

Step1 初始化：初始稀疏度估計值K0=1，初始索引支撐集Γ0=?，迭代步長s，迭代次數n=1，初始試探次數i=1。

Step2 獲取索引集：Γ0=max(|ATyP|,K0)，即從|A*yP|選出前K0個最大值索引存入Γ0。

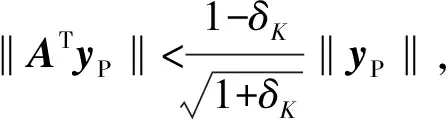
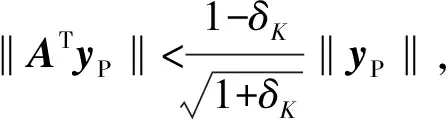
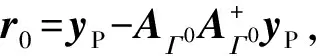
Step6 計算gn=ATrn-1，獲取索引集Jn=max(|gn|,2×card(Γn-1))，card(·)表示集合元素個數，即從|gn|選出前card(Γn-1)個最大元素對應的索引構成集合。

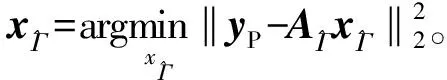
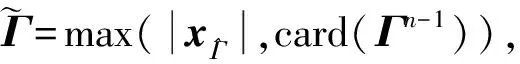
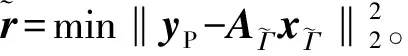
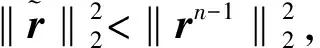
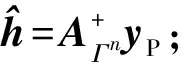
2.3 算法可行性說明

算法將對稀疏度的預估計分為兩個過程，粗略試探過程和精細試探過程。在粗略試探過程，利用冪函數始終增長但增長速率緩慢的特性進行粗略搜索，得到一個粗略的稀疏度估計值；在精細試探過程，以小步長擴大支撐集進行精細搜索，可以保證獲得準確的稀疏度預估值。稀疏度預估計為后面的重構提供了可靠的先驗信息，提高了算法效率，避免了傳統算法對步長的依賴。

根據計算得到最相關的2k個原子構成初始預選集，然后通過回溯剔除不理想原子，改善了估計結果，在保證算法重建精度的同時提高了算法抗噪性能。

在候選集無法達到要求時，需要引進新的原子進行重估，傳統做法是通過原子篩選，再引進L個最相關的原子，隨著支撐集的增大，排序靠后的候選原子為不理想的原子概率也增大，引入這些原子會影響重建效果。為盡量引入理想原子提高重建精度，采用弱選擇原則，通過設置合適閾值來控制選擇原子數量，篩選出大于一定相關性的原子加入支撐集。已有實驗表明[14]，弱匹配參數α在[0.4，0.8]之間取值時可以兼顧算法性能和運算速度。

3 實驗與分析

為比較所提改進的P-SAMP算法與OMP算法、VSStAMP算法及SASP算法在點對點MIMO-OFDM系統下行鏈路的信道估計的性能，本文進行了仿真，驗證所提算法在MIMO-OFDM的下行信道估計中的優勢。仿真實驗所使用的環境為AMD Ryzen 2600X CPU@3.6 GHz,16 GB RAM,Matlab 2018a。假設MIMO-OFDM的天線方案為4×4，即收發天線數目皆為4根，仿真時MIMO-OFDM系統采用16QAM調制，子載波數為512,信道長度為60，并假設系統經歷的是慢衰落，即信道在一個或者多個周期內保持穩定。為了簡便，導頻放置方式為隨機放置。本節仿真中，各算法的迭代停止條件均設為‖rn‖2<ε，其中‖rn‖2代表當前階段的殘差，ε取噪聲功率。采用歸一化均方誤差(Normalized Mean Square Error，NMSE)來衡量估計性能：

(15)

3.1 初始參數的確定

算法首先要對真實稀疏度K進行預估，得到一個略小于K的估計值K0，因此對δK值的選取十分重要。選取合適的δK會使估計出的K0非常靠近真實稀疏度K，以減少迭代次數提升算法效率。通過實驗方法考察約束等距常量δK對稀疏度預估計的影響，在0.25～0.4之間每隔0.05取一個值。圖3比較了K=20條件下不同δK值對稀疏度K的預估，可以看出，δK=0.35時稀疏度預估計的效果最好。同時，對δK取0.35仿真5 000次，得到預估計的K0的平均值為14.581 9，比較接近真實稀疏度K，因此以后的仿真都選取δK=0.35。在粗略試探過程階段，選取合適的搜索步長參數b也十分重要，合適的b值能提高試探速度，因此需要考慮參數b對算法重建時間的影響。由表1可以看出，當b=0.6時，單次平均運行時間最短，故在以后的仿真都取b=0.6。

圖3 稀疏度預估計

搜索步長參數b單次平均運行時間/ms0.55.290.64.930.75.17

接下來通過實驗的方法考查閾值參數α對信號重建性能的影響。α在0.4～0.7 之間每隔0.1取一個值，仿真結果如圖4所示，可見當α= 0.7時，信號的重建恢復率最好，因此之后的仿真都取α= 0.7。

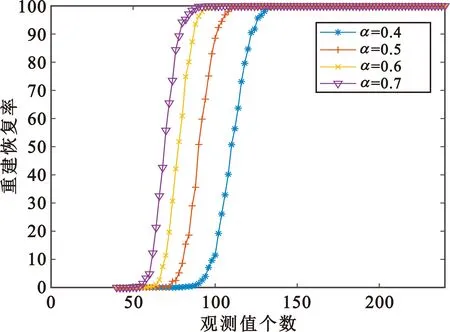
圖4 不同閾值參數α下PSAMP算法的重建恢復率

3.2 性能比較

圖5對比了三種算法在不同信噪比(Signal-to-Noise Ratio,SNR)下的NMSE性能表現，這里使用的導頻數為32。圖中OMP算法效果不好是因為稀疏度未作為先驗信息輸入時，迭代次數不定，且其沒有回溯機制，無法剔除選中的不理想原子，致使算法結果不好；VSStAMP算法引入了變步長思想，過估和欠估的概率下降，但擴充候選集時未引入回溯思想，容易引入大量不理想的原子，影響算法精度；本文提出的PSAMP算法首先對稀疏度進行了預估計，提高了算法效率，同時在第二階段采用回溯機制，得到了更好的信道估計性能。由對比結果可知，VSStAMP和PSAMP算法在0～5 dB信噪比之間時相比OMP有10 dB左右的優勢，且隨著信噪比的增加優勢依舊保持；在0～3 dB下，所提算法性能略低于VSStAMP算法。這是由于PSAMP算法在低信噪比下預估計易出現過估計的情況，進而導致估計結果不佳。在信噪比大于10 dB以后，三種算法的性能均隨著SNR的增大而提高，VSStAMP算法相較OMP算法有4 dB左右的優勢，PSAMP算法的NMSE曲線比VSStAMP低3 dB左右，本文提出的PSAMP算法優于其他算法。

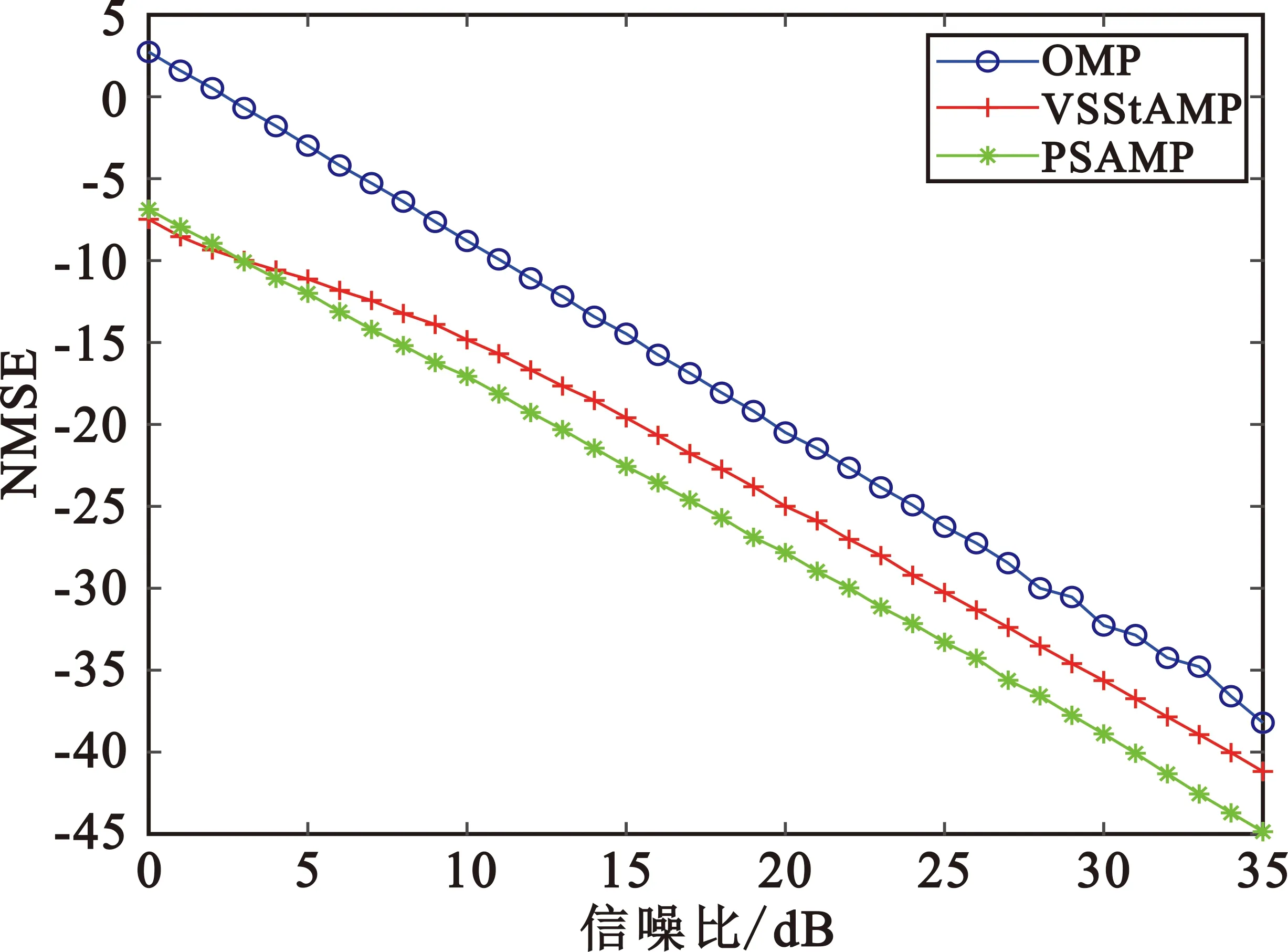
圖5 OMP算法、VSStAMP算法和PSAMP算法在不同信噪比下的均方誤差

在移動通信系統中，接收端收到的信號通常因受到信道的影響而失真，因而需要進行信道估計來均衡信道帶來的影響。因此，比較準確的信道估計能降低系統的誤碼率。圖6給出了導頻數為32時，所采用的三種算法在不同信噪比下的誤比特率性能。從仿真結果可以看出，PSAMP算法和VSStAMP算法相較于OMP算法有明顯優勢，本文提出的PSAMP算法相較于VSStAMP算法在0～10 dB信噪比區間性能相近，但隨著信噪比的增加，為系統帶來的性能改善逐漸明顯，有更低的誤比特率性能；三種算法的曲線在高信噪比處都出現了不光滑的現象，這是對導頻符號選取為隨機導致的，后續的研究將對導頻符號的選取進行優化。

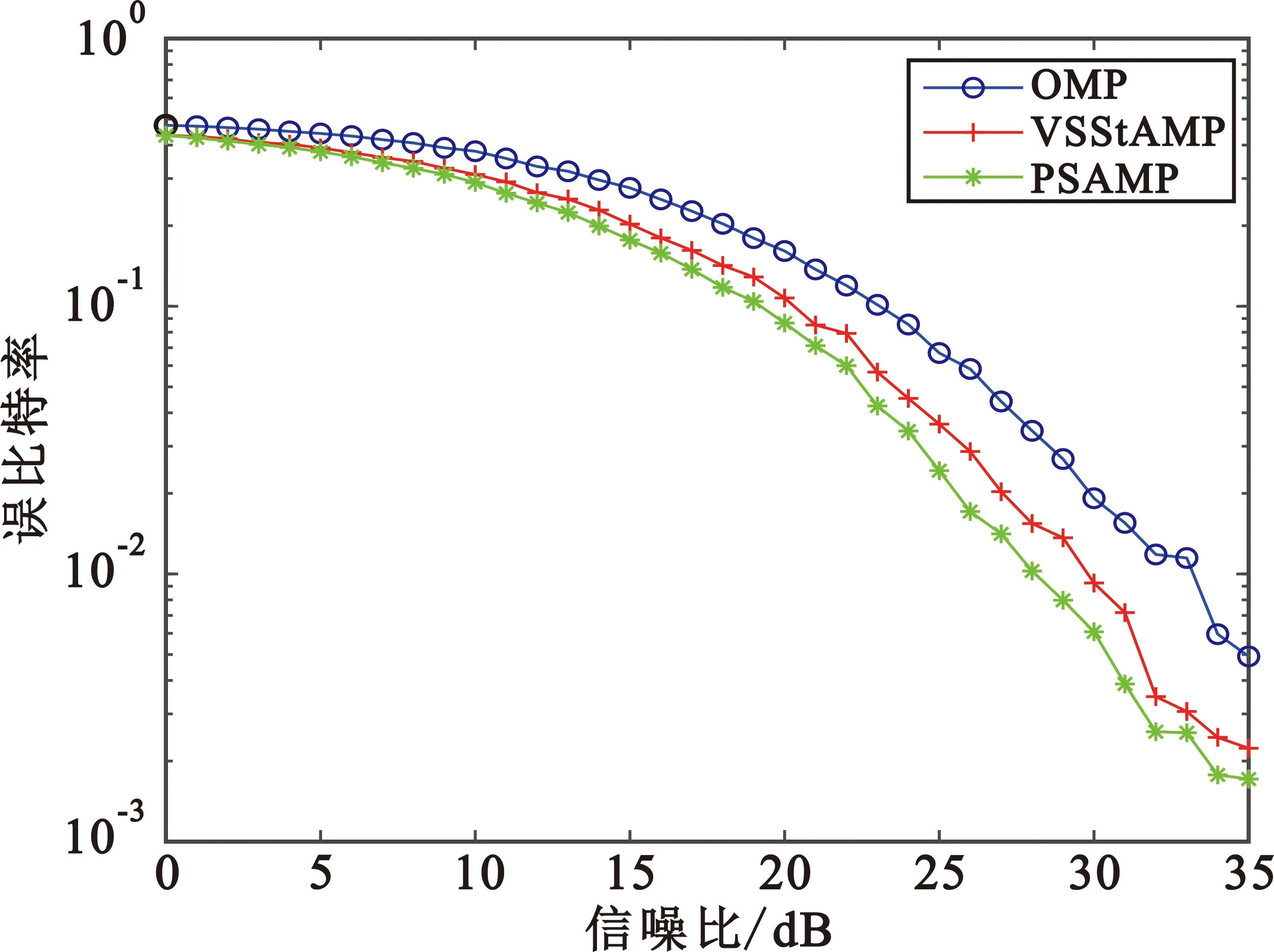
圖6 OMP、VSStAMP和PSAMP算法在不同信噪比下的誤比特率

表2所示的是不同信道估計算法的單次平均運行時間。由表2可知，OMP 算法的運行時間最短，但在稀疏度未知的情況下估計性能較差；本文所提的PSAMP算法和文獻[12]的VSStAMP算法因存在回溯機制，因而運行時間比OMP算法的運行時間長。本文提出的PSAMP算法在重構之前設計了一種冪函數預估計過程，使得后續重構階段可以更快地逼近真實稀疏度，因此算法的運行時間低于VSStAMP 算法。

表2 不同信道估計算法單次平均運行時間

4 結束語

超密集組網不可避免在相鄰小區使用非正交導頻，其帶來的干擾將嚴重影響信道估計的準確性。針對該問題，本文提出了一種使用短導頻的冪函數稀疏度自適應匹配追蹤(PSAMP)算法，實驗仿真驗證了其有效性。

本文利用壓縮感知技術對稀疏信道支撐集進行追蹤時，對導頻符號選取為隨機，盡管它可以與大部分正交基字典保持著不相關，但是仍存在小概率相關性較大，影響數據的傳輸。故在實際應用中，不能在每次數據傳輸之前隨機選取導頻符號，應在系統設計的階段就將對導頻符號固定下來，這對壓縮感知技術在實際中的運用具有重大的意義。