一種基于網(wǎng)格劃分?jǐn)?shù)據(jù)場(chǎng)的雷達(dá)信號(hào)分選方法*

劉峻臣，胡 進(jìn)，何航峰

(中國(guó)船舶重工集團(tuán)公司第七二四研究所，南京 211106)

0 引 言

隨著電子信息技術(shù)的不斷發(fā)展，新的雷達(dá)體制和信號(hào)調(diào)制樣式相繼出現(xiàn)，電子偵察面臨的電磁環(huán)境越來(lái)越復(fù)雜。如何在復(fù)雜的電磁環(huán)境中正確地分選出未知雷達(dá)信號(hào)，一直是電子偵察工作中的重點(diǎn)和難題。

聚類算法是數(shù)據(jù)挖掘中的一種重要算法，它能挖掘未知數(shù)據(jù)間的相關(guān)性，將性質(zhì)相似的數(shù)據(jù)歸為一類[1]。聚類作為一種無(wú)監(jiān)督的分類方法，很適合解決缺乏先驗(yàn)信息的未知雷達(dá)信號(hào)的分類問(wèn)題[2]。K-means聚類算法因收斂快、易于實(shí)現(xiàn)、思想簡(jiǎn)單、不需要先驗(yàn)信息在雷達(dá)信號(hào)分選中應(yīng)用比較廣泛[2]。但是傳統(tǒng)的K-means聚類算法需要人工設(shè)定聚類數(shù)目，并且對(duì)聚類中心敏感，從而影響了雷達(dá)信號(hào)分選準(zhǔn)確率。對(duì)于聚類數(shù)目的確定，一般使用手肘法，但是并不是所有代價(jià)函數(shù)曲線都存在明顯的“肘部”，并且也無(wú)法解決算法對(duì)聚類中心敏感的問(wèn)題。K-means++算法能夠更加合理地給出初始聚類中心，但是當(dāng)數(shù)據(jù)量增加時(shí)，算法的初始化回變得很慢。為了實(shí)現(xiàn)對(duì)聚類數(shù)目和聚類中心的自動(dòng)確定，文獻(xiàn)[3]使用數(shù)據(jù)場(chǎng)對(duì)雷達(dá)信號(hào)進(jìn)行分選，能自動(dòng)選取聚類中心和聚類個(gè)數(shù)，但是需要手動(dòng)設(shè)定影響因子；文獻(xiàn)[4]提出勢(shì)熵的概念，利用勢(shì)熵可以自動(dòng)選取輻射因子，但是運(yùn)算量較大。大部分?jǐn)?shù)據(jù)場(chǎng)使用歐式距離進(jìn)行計(jì)算[5-6]，對(duì)分布多為矩形簇的雷達(dá)信號(hào)進(jìn)行分選時(shí)容易發(fā)生錯(cuò)誤。

本文對(duì)傳統(tǒng)的數(shù)據(jù)場(chǎng)方法進(jìn)行改進(jìn)，使用子空間劃分的方法快速確定影響因子，提高數(shù)據(jù)場(chǎng)的計(jì)算速度，并使用密度閾值清除信號(hào)交疊區(qū)域的網(wǎng)格；針對(duì)雷達(dá)信號(hào)的矩形簇分布，提出使用矩形等效距離替代歐氏距離的方法，從而更準(zhǔn)確地獲得聚類數(shù)目和聚類中心，較好地實(shí)現(xiàn)了雷達(dá)信號(hào)的分選。

1 數(shù)據(jù)場(chǎng)理論

李德毅院士[7]參照傳統(tǒng)物理中場(chǎng)的定義，提出了數(shù)據(jù)場(chǎng)理論。數(shù)據(jù)場(chǎng)理論假定數(shù)據(jù)空間中的點(diǎn)都是具有一定質(zhì)量的粒子，每個(gè)數(shù)據(jù)粒子都會(huì)對(duì)周圍空間產(chǎn)生一定的作用效果，數(shù)據(jù)空間中其他數(shù)據(jù)點(diǎn)將受到該點(diǎn)場(chǎng)力的作用，同時(shí)該粒子也會(huì)受到其他粒子場(chǎng)力的作用。

設(shè)定已知空間Ω中包含有n個(gè)數(shù)據(jù)粒子集合D={x1,x2,…,xn}，其中每一個(gè)數(shù)據(jù)粒子為m維向量xi={xi1,xi2,…,xim}，即使用高斯影響函數(shù)來(lái)表示數(shù)據(jù)場(chǎng)中某一個(gè)數(shù)據(jù)點(diǎn)xa在數(shù)據(jù)中點(diǎn)xb產(chǎn)生的場(chǎng)強(qiáng)函數(shù)如下：

(1)

式中：σ表示影響因子，用來(lái)決定每個(gè)數(shù)據(jù)粒子的作用距離；m為每個(gè)數(shù)據(jù)粒子的等效質(zhì)量；d(xa,xb)為兩點(diǎn)之間的歐式距離。

數(shù)據(jù)場(chǎng)中所有數(shù)據(jù)粒子對(duì)xb產(chǎn)生的場(chǎng)強(qiáng)函數(shù)的和稱為勢(shì)函數(shù)，定義如下：

(2)

由式(2)可知，勢(shì)值和距離成反比，即數(shù)據(jù)密集的地方勢(shì)值大，稀疏的地方勢(shì)值小。

2 基于改進(jìn)數(shù)據(jù)場(chǎng)的雷達(dá)信號(hào)分選方法

2.1 雷達(dá)信號(hào)矩形簇特征

雷達(dá)分選中一般使用雷達(dá)信號(hào)的脈沖描述字(Pulse Descriptor Word,PDW)作為分選依據(jù)，PDW一般包含雷達(dá)的幅度(Pulse Amplitude,PA)、到達(dá)時(shí)間(Time of Arrival，TOA)、載頻(Radio Frequency,RF)、脈寬(Pulse Width,PW)、脈沖到達(dá)角(Direction of Arrival，DOA)[8]。其中，PA穩(wěn)定度不高，TOA在混疊的信號(hào)中無(wú)法直接作為分選依據(jù)，因此本文使用RF、PW和DOA作為信號(hào)分選的參數(shù)。

現(xiàn)代雷達(dá)信號(hào)參數(shù)復(fù)雜多變，在載頻的調(diào)制上一般有固定載頻、載頻捷變、載頻滑變和載頻參差組變。其中，固定載頻由于存在系統(tǒng)測(cè)量誤差，在分布上呈現(xiàn)正態(tài)分布規(guī)律；載頻捷變?yōu)樾盘?hào)載頻在一個(gè)區(qū)間內(nèi)隨機(jī)變化，變化規(guī)律服從均勻分布；載頻參差組變?yōu)樾盘?hào)有多個(gè)頻點(diǎn)，信號(hào)在每個(gè)頻點(diǎn)上持續(xù)一定時(shí)間，然后跳變到下一個(gè)頻點(diǎn)；載頻滑變的分布取決于滑變步長(zhǎng)的大小，當(dāng)步長(zhǎng)較小時(shí)可看作與載頻捷變類似，步長(zhǎng)較大時(shí)與載頻參差組變類似。脈寬的調(diào)制方式一般有固定脈寬、脈寬捷變，其分布規(guī)律與載頻相似。

雷達(dá)信號(hào)的到達(dá)角參數(shù)的改變僅取決于電子偵察系統(tǒng)與輻射源之間的相對(duì)位置，DOA的變化相對(duì)較慢，可以假設(shè)為一個(gè)勻速變化的過(guò)程。DOA參數(shù)的計(jì)算如下式所示：

DOA=DOAs+δ(t)。

(3)

式中：DOAs為初始的DOA參數(shù)，δ(t)為目標(biāo)的角度變化值。DOA的變化在分布上也可看作均勻分布。

為了對(duì)參數(shù)復(fù)雜多變的雷達(dá)信號(hào)進(jìn)行研究，選擇信號(hào)的載頻、脈寬和到達(dá)角中任意兩種參數(shù)進(jìn)行組合，得到可能的雷達(dá)信號(hào)參數(shù)組合如表1所示。

表1 雷達(dá)信號(hào)二維分布形式

為了直觀表現(xiàn)出雷達(dá)信號(hào)參數(shù)在二維空間上的分布特點(diǎn)，將表1中雷達(dá)信號(hào)的各種分布形式展示在二維平面上，如圖1所示。

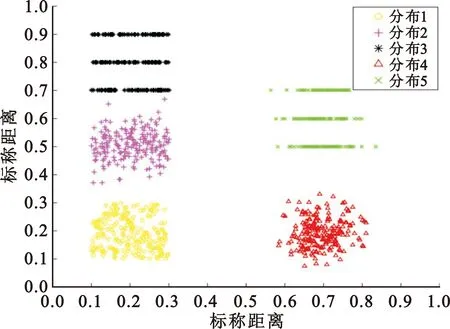
圖1 雷達(dá)信號(hào)分布特征示意圖

結(jié)合表1和圖1可以看出，當(dāng)雷達(dá)信號(hào)的兩個(gè)參數(shù)的調(diào)制類型為捷變或者參差組變時(shí)，雷達(dá)信號(hào)在二維空間上呈現(xiàn)出近似矩形簇的形態(tài)(如圖1中的分布1、分布3、分布5)。

2.2 改進(jìn)距離函數(shù)

傳統(tǒng)的數(shù)據(jù)場(chǎng)在計(jì)算時(shí)使用歐式距離，單個(gè)數(shù)據(jù)點(diǎn)產(chǎn)生的數(shù)據(jù)場(chǎng)的等勢(shì)線在二維空間中體現(xiàn)為以數(shù)據(jù)點(diǎn)為圓心、作用范圍為半徑的圓。當(dāng)數(shù)據(jù)的分布近似圓形簇時(shí)，歐氏距離數(shù)據(jù)場(chǎng)分析可以取得較好的效果。當(dāng)雷達(dá)信號(hào)為圖1中的分布1、分布3、分布5時(shí)，其分布形狀近似為矩形簇，使用歐氏距離數(shù)據(jù)場(chǎng)進(jìn)行分析時(shí)，效果不太理想。為了提高數(shù)據(jù)場(chǎng)對(duì)矩形簇的雷達(dá)信號(hào)分析的效果，本文對(duì)數(shù)據(jù)場(chǎng)中的距離函數(shù)進(jìn)行改進(jìn)，使用矩形等效距離代替歐式距離，使得數(shù)據(jù)場(chǎng)中的單個(gè)數(shù)據(jù)點(diǎn)的作用范圍變?yōu)榫匦危瑥亩岣邤?shù)據(jù)場(chǎng)對(duì)雷達(dá)信號(hào)的分析能力。

以二維空間為例對(duì)數(shù)據(jù)空間中的單個(gè)數(shù)據(jù)點(diǎn)進(jìn)行分析，單個(gè)數(shù)據(jù)點(diǎn)的空間分布如圖2所示。

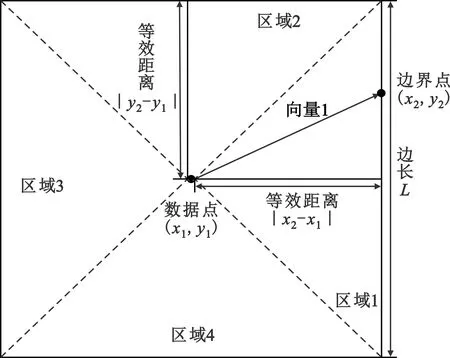
圖2 矩形等效距離原理圖

假設(shè)改進(jìn)的數(shù)據(jù)場(chǎng)中數(shù)據(jù)點(diǎn)產(chǎn)生的作用范圍為邊長(zhǎng)為L(zhǎng)的正方形。將正方形劃分為4個(gè)區(qū)域，求取每個(gè)區(qū)域的等效距離。假設(shè)數(shù)據(jù)點(diǎn)的坐標(biāo)為(x1,y1)，位于正方形邊長(zhǎng)上的任意點(diǎn)為(x2,y2)，則向量1可表示為(x2-x1,y2-y1)。利用向量1在x軸方向和y軸方向上的投影距離對(duì)正方形進(jìn)行區(qū)域劃分：

(4)

對(duì)于不同的區(qū)域，分別求出其等效距離為

(5)

使用兩種距離函數(shù)的數(shù)據(jù)場(chǎng)對(duì)雷達(dá)矩形簇信號(hào)進(jìn)行分析，如圖3所示。

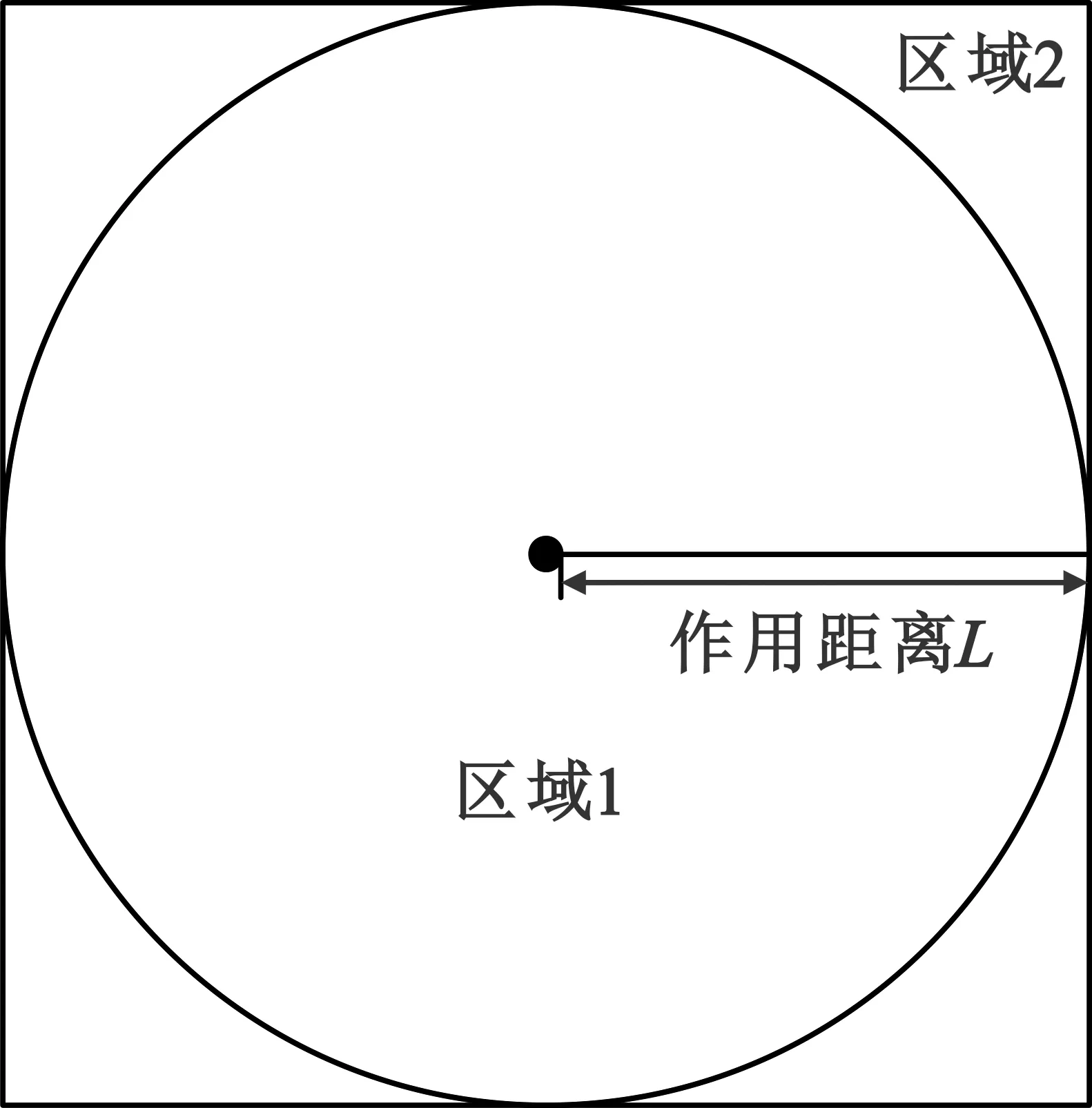
圖3 數(shù)據(jù)場(chǎng)作用范圍對(duì)比

在影響因子相同的情況下，原始數(shù)據(jù)場(chǎng)和矩形數(shù)據(jù)場(chǎng)的作用范圍分別為直徑為2L的圓和邊長(zhǎng)為2L的正方形。當(dāng)數(shù)據(jù)分布為矩形簇時(shí)，有一部分?jǐn)?shù)據(jù)會(huì)落在區(qū)域2中，對(duì)比數(shù)據(jù)場(chǎng)的作用范圍可知，原始數(shù)據(jù)場(chǎng)會(huì)將區(qū)域2中的數(shù)據(jù)點(diǎn)劃分到另外一類中，矩形數(shù)據(jù)場(chǎng)則會(huì)將這部分的數(shù)據(jù)點(diǎn)與中心數(shù)據(jù)點(diǎn)歸為一類，因此，對(duì)于數(shù)據(jù)分布為矩形簇的信號(hào)，使用改進(jìn)的數(shù)據(jù)場(chǎng)能得到更好的分析效果，并且相對(duì)于原始的歐式距離，改進(jìn)的距離函數(shù)在計(jì)算上只有減法和判斷，在運(yùn)算速度上有所提高。

2.3 基于網(wǎng)格劃分的影響因子σ選取方法

由式(2)可知，數(shù)據(jù)對(duì)象的作用距離與σ值的大小成正比。當(dāng)σ值過(guò)小時(shí)，數(shù)據(jù)空間中的每個(gè)數(shù)據(jù)粒子都不能對(duì)其他數(shù)據(jù)粒子產(chǎn)生作用，每個(gè)數(shù)據(jù)粒子相互獨(dú)立，自成一類；當(dāng)σ值過(guò)大時(shí)，整個(gè)數(shù)據(jù)場(chǎng)會(huì)只出現(xiàn)一個(gè)勢(shì)心。上述的兩種情況都不能準(zhǔn)確反映數(shù)據(jù)空間中數(shù)據(jù)的分布情況，所以如何選擇一個(gè)合適的輻射因子值對(duì)數(shù)據(jù)場(chǎng)的構(gòu)建十分重要。

目前常用的影響因子選取方法有兩種。一種是根據(jù)經(jīng)驗(yàn)，在數(shù)據(jù)量小于1 000時(shí)，選取影響因子為0.1，數(shù)據(jù)量增加一個(gè)數(shù)量級(jí)時(shí)，影響因子設(shè)定為0.05[1]。但使用這種方法設(shè)定影響因子不夠靈活，在對(duì)不同類型數(shù)據(jù)進(jìn)行處理時(shí)容易出現(xiàn)錯(cuò)誤。第二種方法為找到勢(shì)熵的最小值，利用勢(shì)熵的最小值來(lái)求取影響因子[4,9]。此方法可以較好地確定影響因子的值，但是運(yùn)算量很大。

本文提出一種基于網(wǎng)格劃分的影響因子選取方法。首先根據(jù)數(shù)據(jù)總數(shù)N來(lái)確定每一維區(qū)間劃分個(gè)數(shù)K[10]：

(6)

式中：m為可調(diào)參數(shù)，m取值越大，劃分網(wǎng)格數(shù)越少；m取值越小，劃分網(wǎng)格數(shù)越多，一般數(shù)據(jù)點(diǎn)數(shù)越多時(shí)，m取值越大，當(dāng)數(shù)據(jù)量在100～10 000時(shí)m通常取值為2～4。歸一化后的數(shù)據(jù)空間的每個(gè)區(qū)間的邊長(zhǎng)為

(7)

定義每個(gè)網(wǎng)格中包含的數(shù)據(jù)點(diǎn)個(gè)數(shù)為網(wǎng)格密度ρ，對(duì)被劃分到一個(gè)網(wǎng)格中的所有數(shù)據(jù)點(diǎn)的參數(shù)求平均值合成一個(gè)新的等效數(shù)據(jù)點(diǎn)，其等效質(zhì)量的數(shù)值設(shè)為網(wǎng)格密度ρ。在最后進(jìn)行數(shù)據(jù)場(chǎng)計(jì)算時(shí)，使用等效數(shù)據(jù)點(diǎn)進(jìn)行計(jì)算，進(jìn)一步提高了數(shù)據(jù)場(chǎng)的計(jì)算速度。

完成網(wǎng)格劃分后，借鑒網(wǎng)格聚類原理，在進(jìn)行數(shù)據(jù)場(chǎng)的計(jì)算時(shí)將兩個(gè)相鄰網(wǎng)格的數(shù)據(jù)點(diǎn)歸為同一個(gè)勢(shì)心。當(dāng)兩個(gè)數(shù)據(jù)點(diǎn)的距離減小時(shí)，兩個(gè)數(shù)據(jù)點(diǎn)會(huì)被歸為一個(gè)勢(shì)心；當(dāng)兩個(gè)數(shù)據(jù)點(diǎn)的距離增加時(shí)，兩個(gè)數(shù)據(jù)點(diǎn)會(huì)被劃分為兩個(gè)勢(shì)心。兩個(gè)數(shù)據(jù)點(diǎn)疊加的勢(shì)F為

(8)

式中：l為單個(gè)網(wǎng)格的邊長(zhǎng)，d為與數(shù)據(jù)點(diǎn)的距離。兩個(gè)數(shù)據(jù)點(diǎn)的勢(shì)函數(shù)在l=d時(shí)相交，當(dāng)交點(diǎn)的勢(shì)為最大值時(shí)，兩個(gè)數(shù)據(jù)點(diǎn)會(huì)被歸為一個(gè)勢(shì)心。用式(8)對(duì)d求一階偏導(dǎo)：

(9)

當(dāng)l=d時(shí)，式(9)等于0。用式(8)對(duì)d求二階偏導(dǎo)，可得

(10)

在l=d點(diǎn)解得式(10)嚴(yán)格小于0的條件為d<σ，此時(shí)F在l=d處取得最大值，因此利用子空間的邊長(zhǎng)l可以確定影響因子為

σ=1.01×l。

(11)

2.4 信號(hào)交疊部分的處理

數(shù)據(jù)場(chǎng)算法的本質(zhì)是基于密度的聚類算法。在兩個(gè)信號(hào)交疊的時(shí)候，交疊處的密度大于兩個(gè)信號(hào)本身的密度，數(shù)據(jù)場(chǎng)算法很容易將兩個(gè)信號(hào)聚類為一個(gè)勢(shì)心，因此本文在網(wǎng)格劃分的基礎(chǔ)上對(duì)信號(hào)交疊部分的網(wǎng)格進(jìn)行處理。首先對(duì)2.3節(jié)中每一個(gè)帶數(shù)據(jù)的網(wǎng)格求取平均得到平均網(wǎng)格密度ρmean為

(12)

式中：N為帶數(shù)據(jù)的網(wǎng)格總數(shù)，ρi為單個(gè)網(wǎng)格的密度。利用網(wǎng)格中數(shù)據(jù)密度的標(biāo)準(zhǔn)差S來(lái)設(shè)置密度閾值，將密度大于平均密度兩倍標(biāo)準(zhǔn)差的網(wǎng)格清除，因此密度閾值ρthreshold的設(shè)定如下：

ρthreshold=ρmean+2×S。

(13)

2.5 改進(jìn)數(shù)據(jù)場(chǎng)的雷達(dá)信號(hào)分選方法

2.5.1 數(shù)據(jù)預(yù)處理

本文使用RF、PW和DOA作為信號(hào)分選的參數(shù)。為了確保聚類算法不受量綱的影響，多維數(shù)據(jù)聚類時(shí)需要對(duì)數(shù)據(jù)進(jìn)行歸一化處理。假設(shè)需要對(duì)N個(gè)PDW進(jìn)行分選，其歸一化過(guò)程如下：

(14)

式中：i表示PDW的第i維參數(shù),i=1,2,3；j表示第j個(gè)數(shù)據(jù),j=1,2,…,N。

2.5.2 算法流程

首先對(duì)信號(hào)PDW進(jìn)行歸一化處理，然后使用網(wǎng)格劃分方法對(duì)數(shù)據(jù)空間進(jìn)行劃分，根據(jù)網(wǎng)格的長(zhǎng)度確定數(shù)據(jù)場(chǎng)的影響因子，并且對(duì)交疊的高密度網(wǎng)格進(jìn)行清除處理，通過(guò)矩形數(shù)據(jù)場(chǎng)的分布獲得聚類數(shù)目和初始聚類中心，最終使用K-means均值算法完成信號(hào)分選。算法的總體流程如圖4所示。

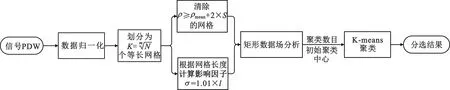
圖4 算法總體流程圖

3 仿真實(shí)驗(yàn)

3.1 矩形數(shù)據(jù)場(chǎng)測(cè)試

為了測(cè)試矩形數(shù)據(jù)場(chǎng)對(duì)雷達(dá)信號(hào)的分析效果，使用原始數(shù)據(jù)場(chǎng)和矩形數(shù)據(jù)場(chǎng)分別對(duì)圖1中5種分布的數(shù)據(jù)進(jìn)行分析測(cè)試，其中數(shù)據(jù)場(chǎng)的影響因子范圍設(shè)置為0.01～0.15，增加步長(zhǎng)為0.01，結(jié)果如表2所示。

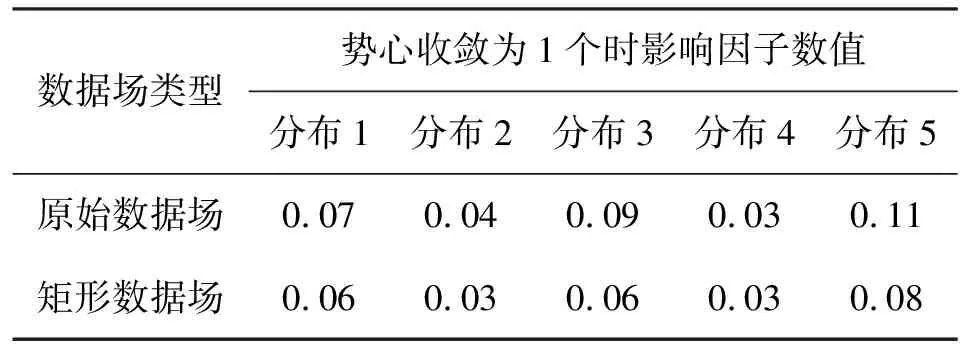
表2 數(shù)據(jù)場(chǎng)對(duì)比測(cè)試效果

由表2可以得出，當(dāng)數(shù)據(jù)為分布1、分布3和分布5時(shí)，矩形數(shù)據(jù)場(chǎng)比原始數(shù)據(jù)場(chǎng)更快收斂到正確的勢(shì)心個(gè)數(shù)；當(dāng)數(shù)據(jù)為分布2和分布4時(shí)，矩形數(shù)據(jù)場(chǎng)和原始數(shù)據(jù)場(chǎng)保持相近的分析能力，因此使用矩形場(chǎng)對(duì)雷達(dá)信號(hào)進(jìn)行分析時(shí)可以獲得比原始數(shù)據(jù)場(chǎng)更好的分析效果。

3.2 信號(hào)分選測(cè)試

本文使用Matlab對(duì)算法進(jìn)行仿真驗(yàn)證，仿真信號(hào)參數(shù)如表3所示，并且在仿真時(shí)對(duì)各個(gè)參數(shù)加入一定的高斯測(cè)量誤差。

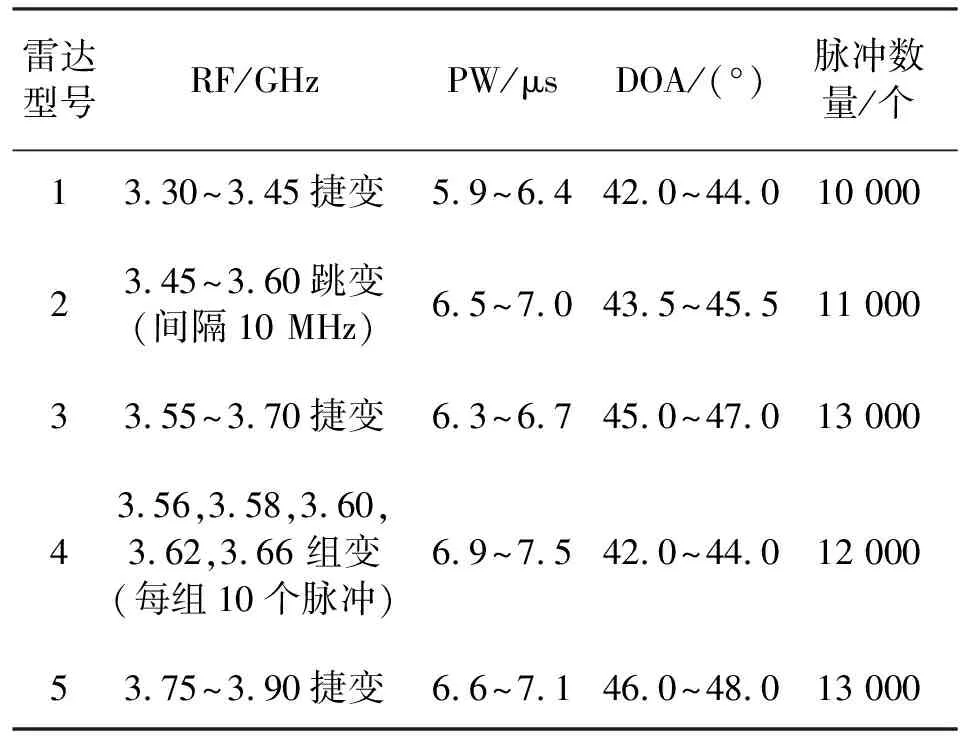
表3 仿真信號(hào)參數(shù)

對(duì)仿真的雷達(dá)信號(hào)分別使用原始數(shù)據(jù)場(chǎng)和改進(jìn)后數(shù)據(jù)場(chǎng)進(jìn)行計(jì)算，其中原始數(shù)據(jù)場(chǎng)的影響因子取值為0.03，改進(jìn)后數(shù)據(jù)場(chǎng)的網(wǎng)格劃分參數(shù)m取值為4，得到的數(shù)據(jù)場(chǎng)二維圖如圖5～7所示。

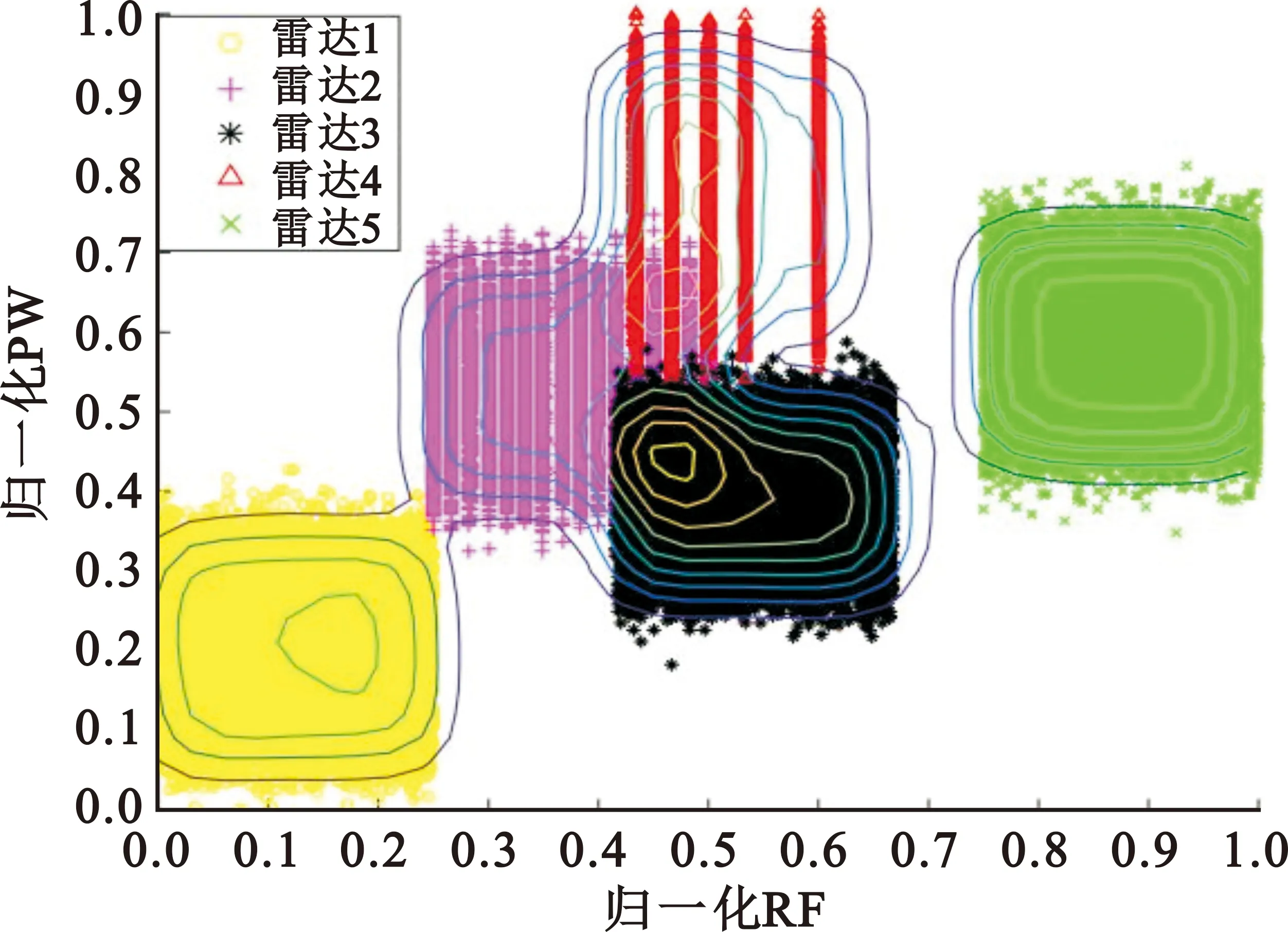
(a)原始數(shù)據(jù)場(chǎng)

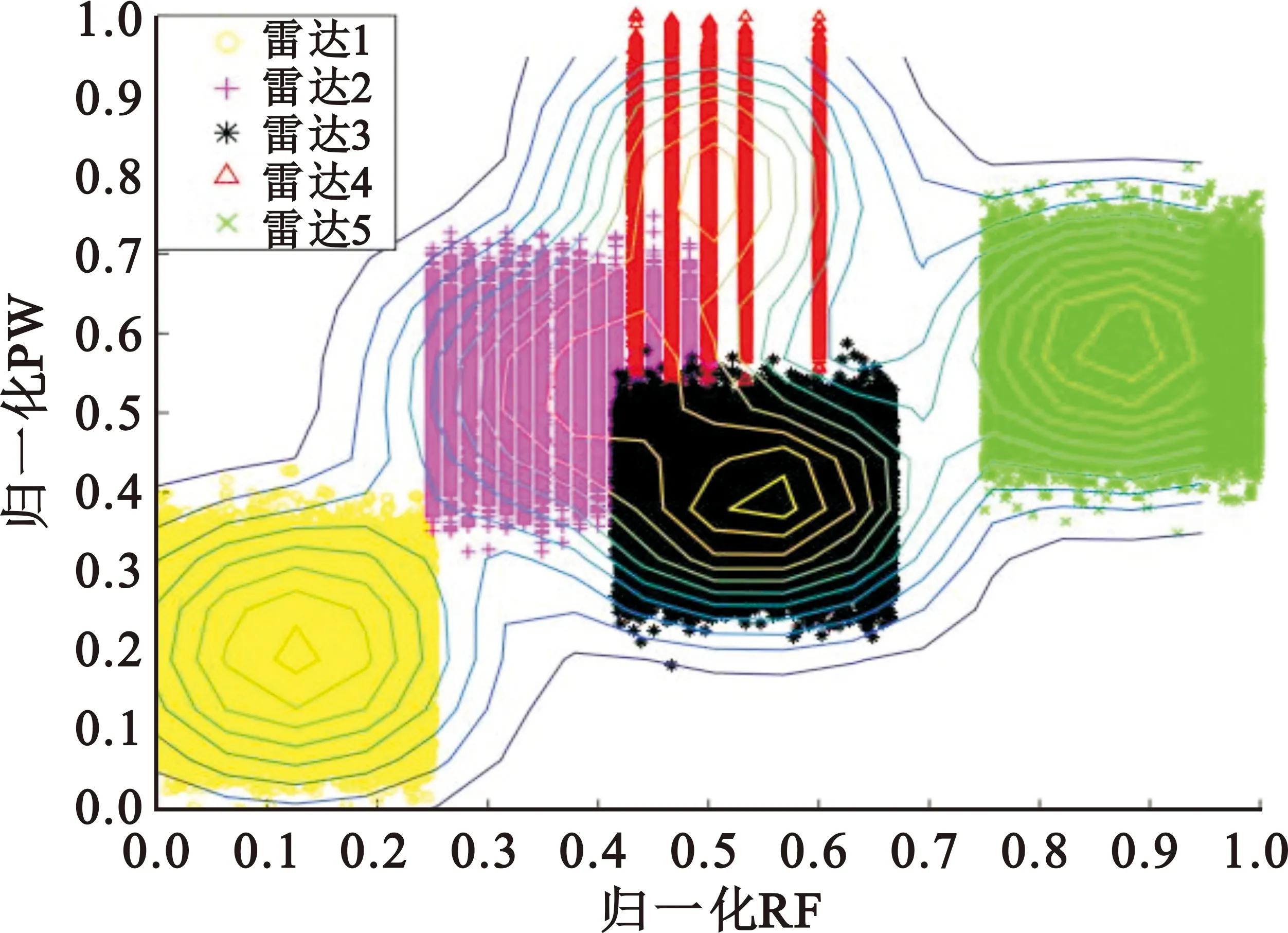
(b)改進(jìn)數(shù)據(jù)場(chǎng)圖5 載頻和脈寬數(shù)據(jù)場(chǎng)二維圖

(a)原始數(shù)據(jù)場(chǎng)

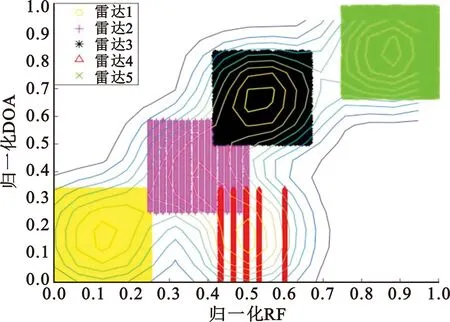
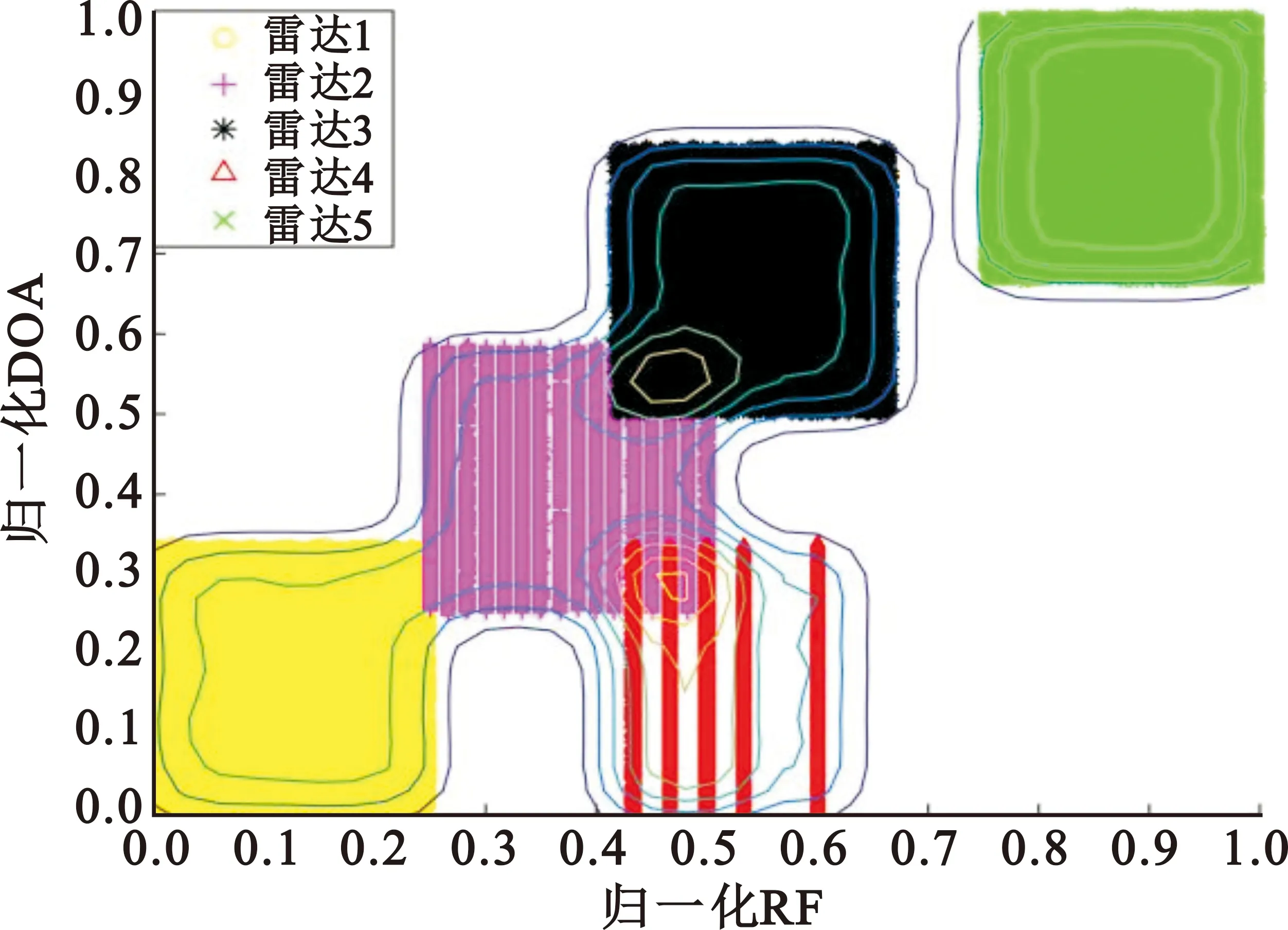
(b)改進(jìn)數(shù)據(jù)場(chǎng)圖6 載頻和方位角數(shù)據(jù)場(chǎng)二維圖

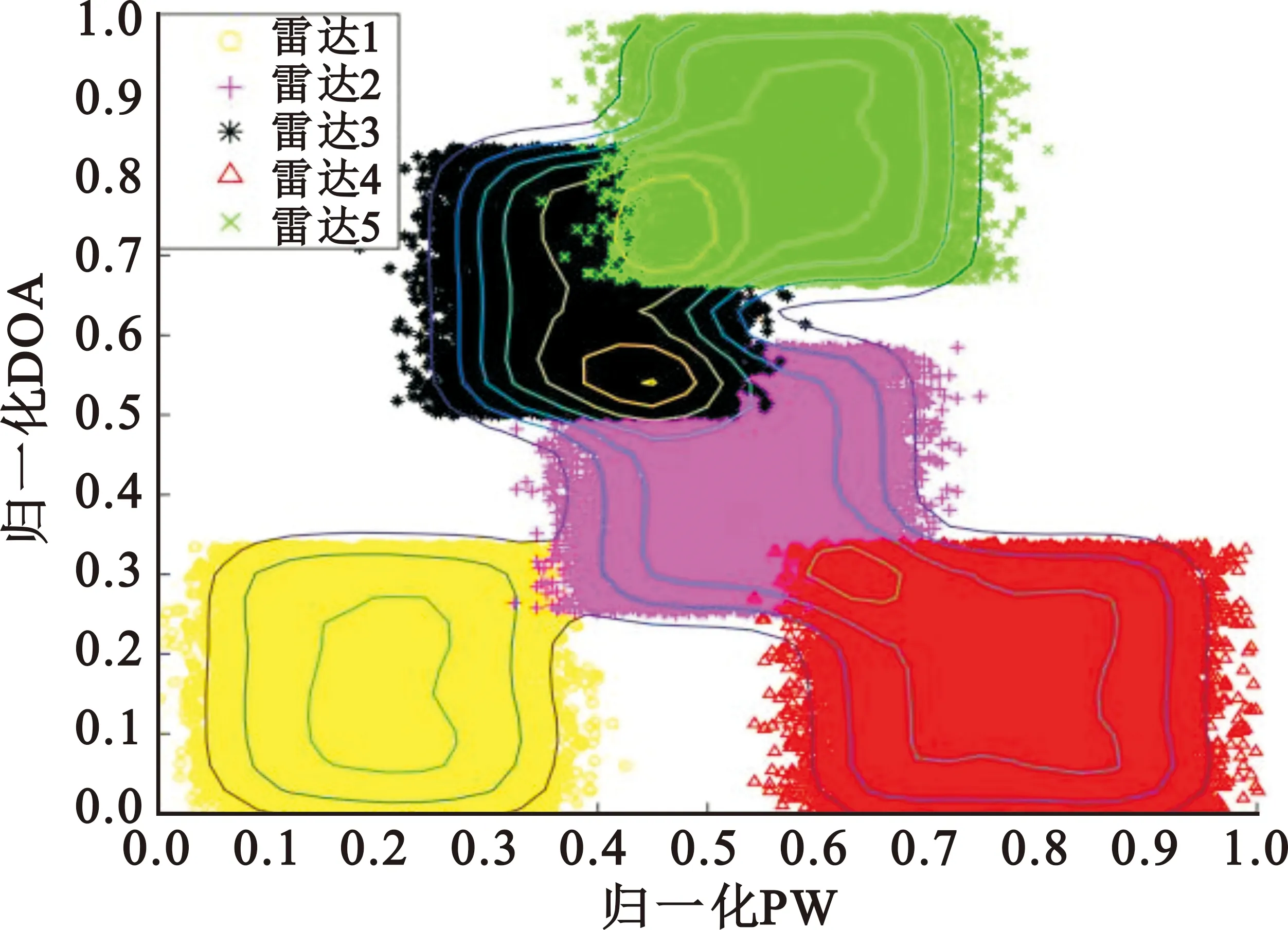
(a)原始數(shù)據(jù)場(chǎng)

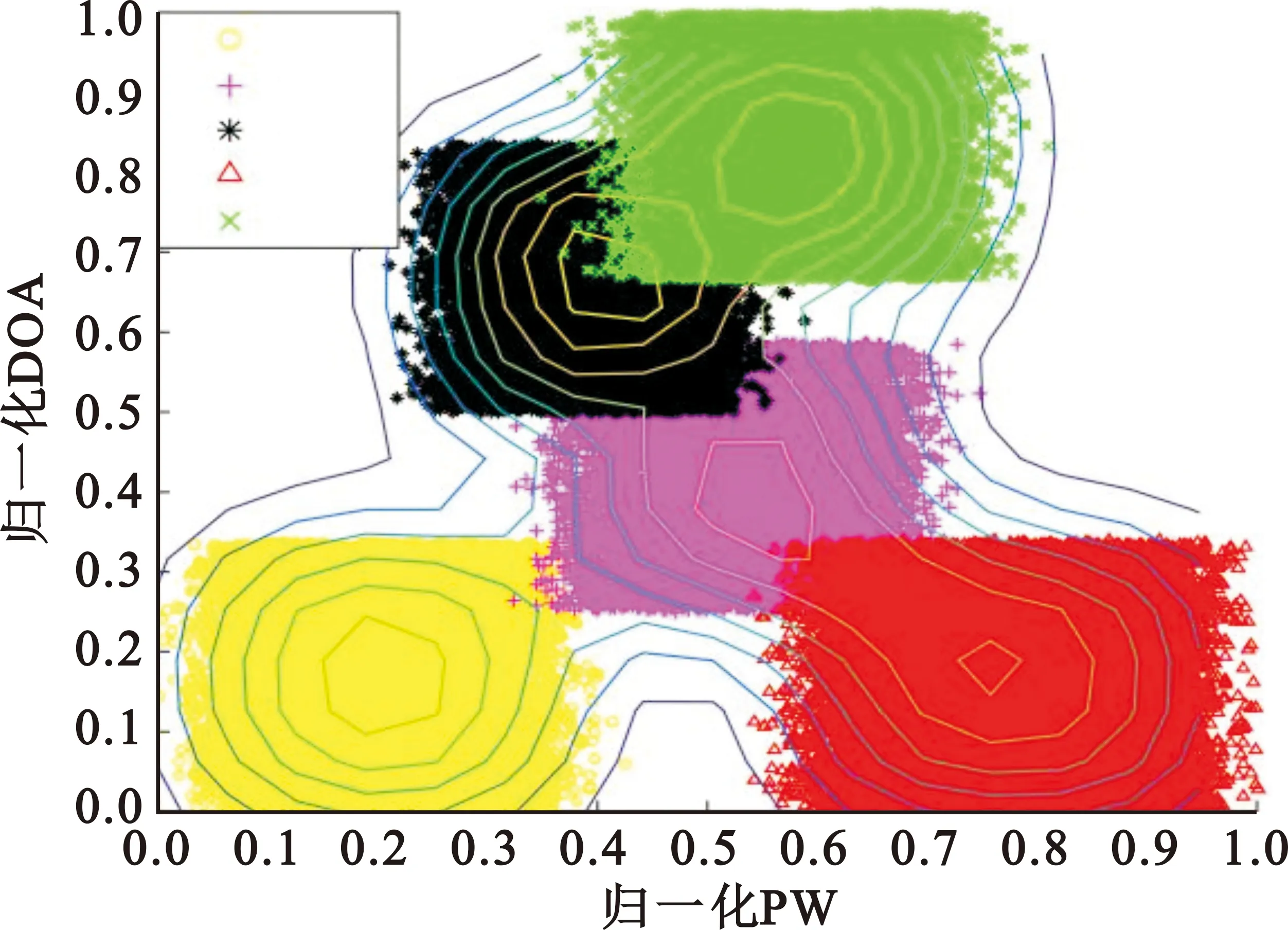
(b)改進(jìn)數(shù)據(jù)場(chǎng)圖7 脈寬和方位角數(shù)據(jù)場(chǎng)二維圖

根據(jù)數(shù)據(jù)場(chǎng)的定義可知，影響因子取值越大，單個(gè)數(shù)據(jù)點(diǎn)的作用范圍越大，數(shù)據(jù)場(chǎng)的勢(shì)心數(shù)減少；影響因子取值越小，單個(gè)數(shù)據(jù)點(diǎn)的作用范圍越小，數(shù)據(jù)場(chǎng)的勢(shì)心數(shù)增加。由圖5(a)中可以看出，雷達(dá)4被數(shù)據(jù)場(chǎng)分為了兩個(gè)勢(shì)心，如果需要使數(shù)據(jù)場(chǎng)中的雷達(dá)4變?yōu)?個(gè)勢(shì)心，則需要增大影響因子的值，但此時(shí)雷達(dá)2和雷達(dá)3被劃分為一個(gè)勢(shì)心，要使其被數(shù)據(jù)場(chǎng)分為兩個(gè)勢(shì)心，則需要減小影響因子的值，與雷達(dá)4的劃分需求矛盾，圖6(a)和圖7(a)均存在類似問(wèn)題。由圖5(b)、圖6(b)和圖7(b)可以看出，對(duì)于同樣的雷達(dá)信號(hào)，改進(jìn)的數(shù)據(jù)場(chǎng)方法相比于傳統(tǒng)方法，可以更好地確定雷達(dá)的數(shù)目和聚類中心。

使用手肘法(聚類個(gè)數(shù)范圍設(shè)定為1～7)，傳統(tǒng)數(shù)據(jù)場(chǎng)(影響因子與改進(jìn)數(shù)據(jù)場(chǎng)求得的影響因子0.063 1保持一致)和改進(jìn)數(shù)據(jù)場(chǎng)對(duì)雷達(dá)信號(hào)進(jìn)行100次蒙特卡洛實(shí)驗(yàn)，得到結(jié)果如表4所示。

表4 聚類個(gè)數(shù)算法迭代時(shí)間

由表4可以看出，手肘法因?yàn)樾枰褂枚鄠€(gè)k值(聚類個(gè)數(shù))進(jìn)行聚類和計(jì)算損失值，運(yùn)算速度最慢；改進(jìn)的數(shù)據(jù)場(chǎng)方法因只需要對(duì)網(wǎng)格合并后的數(shù)據(jù)點(diǎn)進(jìn)行計(jì)算，并且避免了歐氏距離的計(jì)算，運(yùn)算速度最快。取數(shù)據(jù)場(chǎng)計(jì)算后的峰值(勢(shì)心個(gè)數(shù))作為聚類個(gè)數(shù)，可以得到數(shù)據(jù)的聚類個(gè)數(shù)為5個(gè)，得到聚類中心如表5所示。

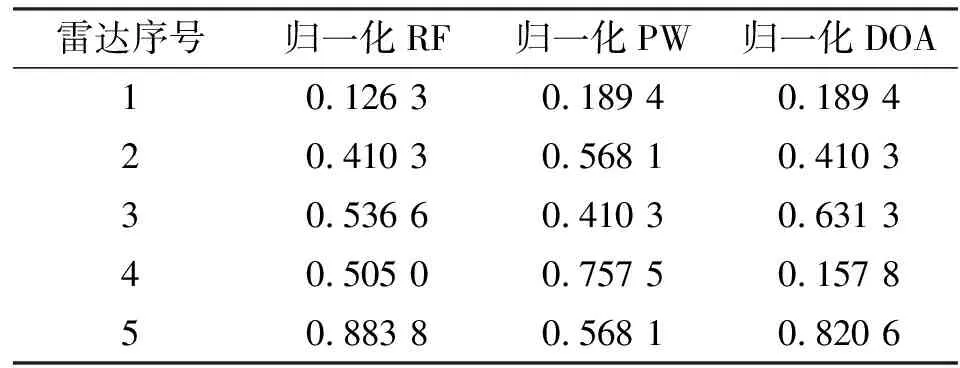
表5 初始聚類中心

使用5作為K-means算法的聚類數(shù)目，表5中的參數(shù)作為K-means算法的初始聚類中心，對(duì)雷達(dá)信號(hào)進(jìn)行100次蒙特卡洛實(shí)驗(yàn)，對(duì)分選正確率和運(yùn)行時(shí)間取平均值，對(duì)比原始K-means算法和K-means++算法，得到的結(jié)果如表6所示。

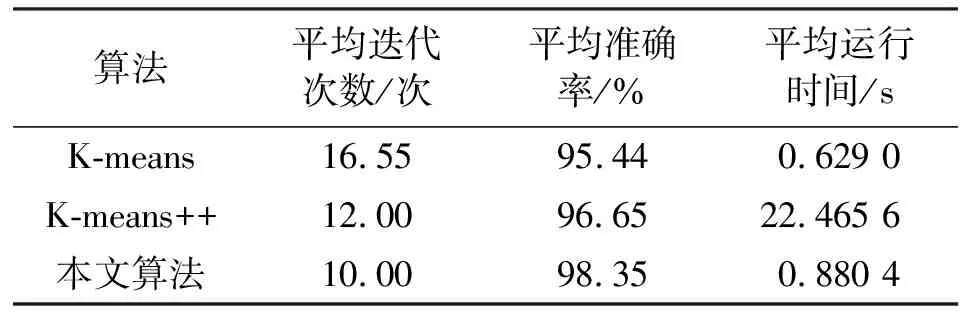
表6 算法準(zhǔn)確率與運(yùn)行時(shí)間對(duì)比

由表6可以看出，改進(jìn)后算法相比于傳統(tǒng)的K-means算法，雖然運(yùn)行時(shí)間有所增加，但是算法的迭代次數(shù)減少，分選準(zhǔn)確率更高；K-means++算法雖然有較高的準(zhǔn)確率，但是運(yùn)行速度很慢。K-means算法、K-means++算法和本文算法的迭代次數(shù)折線圖(運(yùn)行30次)如圖8所示。

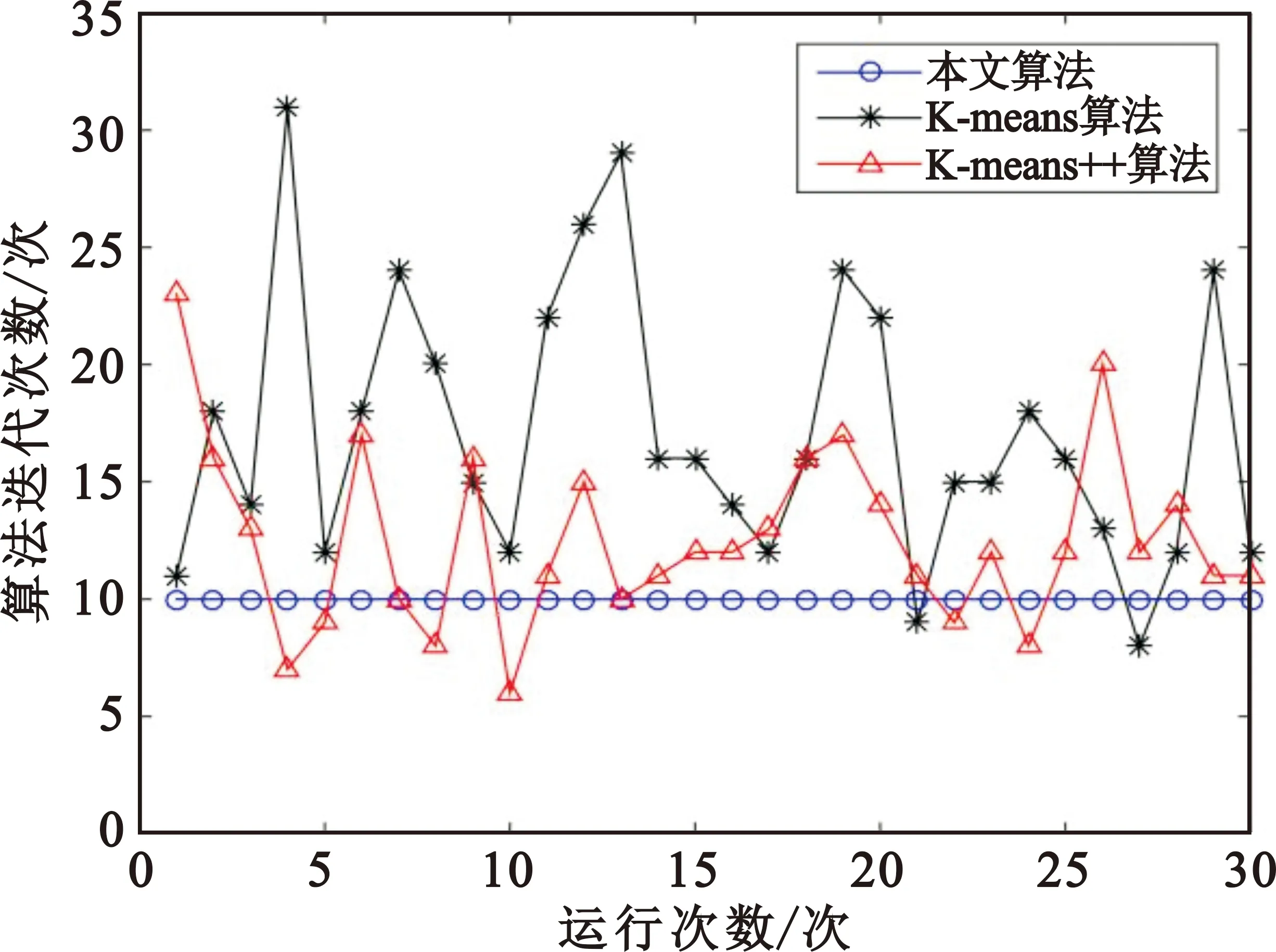
圖8 算法迭代次數(shù)對(duì)比

由圖8可以看出，改進(jìn)的數(shù)據(jù)場(chǎng)算法在提供了聚類數(shù)目和初始聚類中心后，算法的迭代次數(shù)趨于穩(wěn)定，只提供聚類數(shù)目的K-means算法和K-means++算法的迭代次數(shù)不夠穩(wěn)定，每次運(yùn)行的迭代次數(shù)變化較大。

4 結(jié)束語(yǔ)

本文針對(duì)雷達(dá)信號(hào)的特點(diǎn)，對(duì)傳統(tǒng)的數(shù)據(jù)場(chǎng)算法進(jìn)行改進(jìn)，使用矩形等效距離替代原始?xì)W式距離，并且利用網(wǎng)格劃分的方法，快速確定影響因子，清除信號(hào)交疊處的高密度網(wǎng)格，最后結(jié)合K-means算法對(duì)信號(hào)進(jìn)行聚類分選。仿真實(shí)驗(yàn)表明，網(wǎng)格劃分?jǐn)?shù)據(jù)場(chǎng)算法能更好地求取聚類個(gè)數(shù)和聚類中心，并且能夠減少K-means算法的迭代次數(shù)，提高數(shù)據(jù)場(chǎng)計(jì)算速度和分選準(zhǔn)確率，具有一定的參考價(jià)值。但文中只給定了網(wǎng)格劃分中m參數(shù)的選取策略，對(duì)于m參數(shù)的自動(dòng)化選取還有待進(jìn)一步研究。