摒棄以形定量，直抵概念本質

周海斌

摘要：一些教師在實際教學中，照搬教材中靜態的平面圖形，教學方法單一，使學生一開始就形成“量的均分等同于形的均分”的刻板印象，沒有真正理解分數的本質。對此，重構“認識分數”第一課時的教學，重點借助天平讓學生感受“量”的均分，再通過“形”與“量”的變化對比讓學生理解分數的本質，并且由“量”到“數”升華學生對分數意義的理解，為后續單位“1”的教學埋下伏筆。

關鍵詞：分數問題;分數概念;圖形;數量

一、教師和學生對一道分數問題的錯誤認識

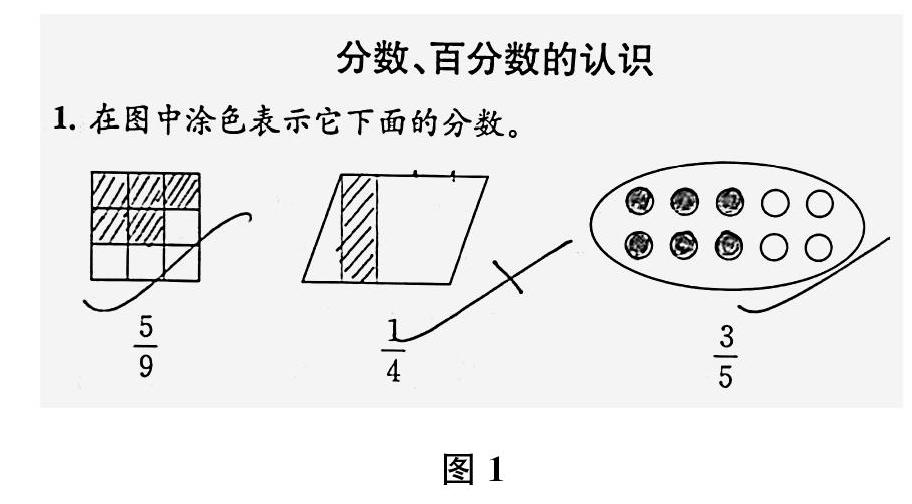
學校組織教師互查互評作業批改情況。我檢查的是一位剛工作的年輕教師。一道六年級的復習題，學生解答和教師批改的情況如圖1所示。

我指著中間打了“×”那幅圖，問那位年輕教師：“學生錯在哪兒？”她說：“他沒有平均分。”我繼續問：“圖中，學生不是有等分點了嗎？”她找來尺和筆作圖，得到圖2，說道：“你看，這是5份，而且大小不一。”我追問：“怎樣才算平均分？”她擦掉之前學生和她畫的，重新作圖，得到圖3。我心想下周的學科組培訓內容有了——事實上，這里只要涂色面積是平行四邊形的14就行了，和形狀無關，畫成長方形、三角形或平行四邊形都不重要。

教師出現這樣的錯誤，那學生呢？隨后，我拿著上述學生解答在六年級學生中做了調查：“這樣涂色算錯嗎？”528名學生中有186人與年輕教師觀點一致，約占35.2%。這一比例著實不低。

二、對教學內容和現狀的深思

分數是從三年級就開始學習的概念，為什么剛入職的教師和六年級的學生會犯這樣的錯誤？問題出在哪兒？得從教學內容和現狀入手分析。

（一）數學歷史追溯

追溯分數的起源有三種視角。從比例關系看，《周禮·考工記》記載“六分其金而錫居一”，就是錫占六分之一的意思。這是對部分與整體或兩個部分之間關系的數學表示，它們之間的不同占比或配比就產生了分數。從度量意義看，《商鞅量》記載“大良造鞅，爰積十六尊（寸）五分尊（寸）壹為升”，這里的“五分”表示五等分得到分數單位五分之一，“壹”表示取其中的一個分數單位。這里的分數是用計數單位（標準）度量被測對象的結果。從整數除法看，《九章算術》中的“合分術”云：“實如法而一，不滿法者，以法命之。”這里的“命之”即“命分”。整句話意為：“……如不能除盡，則定義一個分數。”

（二）教材編排解析

研讀人教版和蘇教版小學數學教材發現，它們都是分兩個階段安排分數概念教學的。第一個階段，從“比例關系”視角出發，通過平均分產生部分和整體的量的對比，讓學生初步感知和體會分數。第二個階段，延續“比例關系”視角，引出單位“1”，定義分數和分數單位概念;并且從“整數除法”視角出發，使得分數與除法建立聯系，拓展分數的內涵。這樣的編排既遵循知識的邏輯體系，又尊重學生的認知規律。

在素材選取上，兩個版本的教材也有相似之處。如第一個階段的第一課時，人教版例題選取的是“分月餅”情境，蘇教版例題選取的是“分蛋糕”情境;習題也大致相同，多以長方形、圓等幾何圖形為背景。可見在第一個階段，教材都是通過“形”的均分來刻畫“量”的均分的。究其原因，教材是靜態的、平面的，引導學生通過視覺感受量的均分更為方便。

（三）教學現狀掃描

第一個階段的分數概念教學至關重要，尤其是第一課時，它是學生已有數概念的一次擴展，同時為后續進一步學習分數奠定基礎。無論追溯數學的歷史，還是解析教材的編寫，第一個階段第一課時的教學都應該從“比例關系”出發，引入“量的均分”。

但是，一些剛入職的年輕教師對知識理解不深刻，對學情把握不準確，對分數的意義和分數的教學缺乏正確認識。同時，由于長期存在“教教材”的錯誤傾向，一些教師在實際教學中，照搬教材中靜態的平面圖形，教學方法單一，使學生一開始就形成“量的均分等同于形的均分”的刻板印象，沒有真正理解分數的本質。后期的教學又沒能將分數由比例關系提升到除法意義，使部分學生到了六年級還停留在“形”的水平。

三、對教學過程的重構

基于以上分析，我對《認識分數》第一課時的教學進行了重構。

（一）借助天平感受“量”的均分，激發創造分數的動機

1.感受“量”的均分。

師（課件出示動畫情境）大雄和小叮當分年糕，怎么分才公平？還剩下一塊，該怎么分呢？

（教師給出實驗材料，用橡皮泥代替年糕。學生小組合作操作天平，將剩下的“年糕”分成相等的兩部分，然后展示交流。）

師如果把其中一個壓扁了，數量有無變化？

（學生小組合作，借助天平驗證“年糕”的“形”變了，但“量”不變。）

師每人分到的數量一樣多，在數學上叫作平均分。

2.激發創造分數的動機。

師現在每人分到了多少個？

生半個。

師數學是研究數量的學科，既然一個可以用“1”來表示，那么半個可以創造什么數來表示呢？

（學生在紙上畫畫寫寫，嘗試創造“新數”。）

[設計意圖：借助天平稱重，將橡皮泥變形，讓學生初步感受平均分的實質：分的是“量”，而不是“形”。半個用什么數表示？當整數不適用時，便引發學生的認知沖突，產生創造分數的動機。]

（二）優化形式，賦予意義，經歷分數產生的過程

1.優化分數形式。

師（展示學生創造的分數：、、，0.5，12）這些形式好在哪里，缺點又是什么？

生幾位同學把“1”“一”“個”寫一半，我覺得挺有意思的，但是不容易把握，一不小心就寫錯了，而且有時候看不懂，容易讓人誤解。

生我在超市見過0.5元，它是1元的一半。

生（指著12）這個數讀作二分之一，也表示一半，是我爸告訴我的。

生我覺得12最好，即使你沒學過數學，也能一眼看出它表示半個，因為上面的1是下面的2的一半。

師同學們寫的這些數都有一定的價值，講得也非常好。尤其是最后一個，正是我們今天要研究的數——分數。

2.賦予分數意義。

師這個數與以往學過的數有什么不同？

生以前的數都是左右寫的，這個是上下寫的，而且中間還有一條線。

生中間的線叫分數線，上面的數叫分子，下面的叫分母。

師猜一猜：數學家為什么用2和1組成這個數？

生因為把一個年糕分成2份，表示其中的1份。

生應該說全了，是平均分。

生把一個年糕平均分成2份，其中的1份就是它的12。

師這一份是整個年糕的12，那么另一份呢？

生也是整個年糕的12。

師如果我把這一份搓成其他形狀，它還是整個年糕的12嗎？

生是的。

師形狀變了，為什么還是12呢？

生盡管形狀變了，但是它的數量沒有變，所以它仍然是整個年糕的12。

師（課件演示）現在把這個年糕平均分成3份，那么1份是它的幾分之一？

生13。

……

師把一個年糕平均分成幾份，其中的一份就是它的幾分之一。

[設計意圖：盡管部分學生通過各種途徑已經知道分數，但是分數為什么這樣寫、它的本質意義是什么，學生并不清楚。任何符號都是形式和意義的統一體，分數的形式反映了其意義。通過分數形式的再創造，不僅能激發學生的創新意識，培養創造能力，而且自然地過渡到分數意義的理解。通過年糕的變形，讓學生初步感知分數反映的是“量”之間的關系，“形”是非本質屬性。]

（三）“形”與“量”變化對比，理解分數的本質

1.“做”分數。

師任選兩張白紙，折一折，涂一涂，說一說你創造了幾分之一。

……

2.“比”分數。

師（出示圖4）這是兩個相同的長方形，但是涂色部分形狀不同，為什么都能表示14呢？

生因為它們都是把長方形平均分成4份，涂了其中的1份。

師這兩個形狀不同的涂色部分大小一樣嗎？

生一樣大，因為它們都是長方形的14。

師（課件演示，如圖5）現在把圖形放大，這1份能還表示14嗎？

生能。

師這1份不是變大了嗎？

生雖然這1份變大了，但整個圖形也一起放大了，仍然是平均分成4份，涂了其中的1份。

師（出示圖6）這幾個圖形形狀、大小都不一樣，為什么涂色部分都能表示14呢？

生因為它們都是把圖形平均分成4份，涂了其中的1份。

師（出示圖7）這兩個涂色部分一樣大，為什么一個表示14，另一個表示16呢？

生因為兩張長方形紙大小不同，平均分的份數也不同。

師如果兩張紙大小相同呢？分數表示變嗎？

生不變。

師所以，分數表示是由什么決定的？

生平均分的份數。

[設計意圖：分數反映的是比例關系，這是學生認識上的一次飛躍。這一環節在“形”和“量”的不斷變化中，引導學生聚焦“量”與“量”之間的比例關系，避開“形”的誤導，初步感知分數的本質意義。]

（四）由“量”到“數”，升華意義的理解

師（出示一個被平均分成8份的長方形）看到這個圖形，你能想到幾分之一？

生18。長方形被平均分成了8份，1份就是18。

師（課件演示，如圖8）現在這8個小長方形變成了8個玩具，你還能想到18嗎？

生能。

師可是，這8個玩具大小、形狀都不同呀？

生可以把它們看作一樣的。

生它們都是同一個系列的玩具。

生可以只看數量，因為是8個，所以是18。

師咱班有多少位同學？你又能想到幾分之一？

生45，145。

[設計意圖：避開了“形”的誤導，學生還會對“量”產生思維定式。進一步變式，將“形”和“量”抽象成物體個數，確認本質屬性，摒棄非本質屬性，以升華學生對分數意義的理解，同時讓學生體會到“數學是人們對客觀世界的定性把握和定量刻畫”。此外，從一個圖形的平均分變為一些玩具的平均分，已經自然地過渡到第二個階段的內容，為學生理解單位“1”埋下了伏筆。]

參考文獻：

[1] 滕艷輝.以“無名”命“微數”——論中國十進制小數的起源與發展[J].遼寧師范大學學報（自然科學版），2010（3）.