基于節點耦合技術的螺栓強度可靠性分析

李永華，王百發，殷浩，孫琦

(大連交通大學 機車車輛工程學院，遼寧 大連 116028)*

螺栓作為起緊固連接作用的機械基礎件，標準和通用程度極高，具有結構簡單，拆裝方便等優點.螺栓的材料屬性以及工作過程中所受載荷具有隨機性，螺栓失效會導致機械零部件甚至整個機械系統的功能失效，因此對螺栓強度進行可靠性分析是十分必要的.傳統的螺栓強度可靠性分析基于MPC接觸方法和蒙特卡羅法進行.接觸分析耗時長，蒙特卡羅法抽取的樣本點數量龐大，導致傳統的螺栓強度可靠性分析耗時，難以實現.

惠燁等[1]基于結合面變形和構件變形的耦合關系，提出在構件間增加虛擬材料層反映結合部非線性特性的假設并建立包含結合部特性的模型，提高了螺栓和構件整體分析的準確性；李玲等[2]對螺栓與結合面因素進行綜合考慮，運用功率譜函數以及WM函數表征結合面微觀特征，利用Mindlin理論和統計學方法建立了能正確反映螺栓結合面剛度的分析模型；姚星宇等[3]將層單元方法應用到螺栓連接部位模擬中，給出其參數化建模方法，并證實了該方法在實際結構應用中的有效性；孫志勇等[4]基于薄層單元參數與模態參數的關系，建立響應面，并采用遺傳算法實現薄層單元參數的優化辨識；Mael Couchaux等[5]基于增強束理論，建立了預測螺栓連接彈性行為的機械模型，可對螺栓力進行較為精確的評估.以上研究提高了接觸區域建模的精確度，使螺栓強度分析結果更接近于工程實際，然而并未解決傳統螺栓強度可靠性分析耗時嚴重的問題.

本文以某地鐵司機室座椅連接螺栓為研究對象，建立其節點耦合模型進行強度分析，并與接觸非線性分析的結果進行對比.基于節點耦合技術和響應面法對螺栓強度可靠性進行分析，該可靠性分析方法可在極大程度上節省分析時間.

1 理論基礎

1.1 節點耦合技術

螺栓在實際工作的過程中，通過預緊力將多個部件連接起來.各個部件主要通過接觸來傳遞力和力矩.可以采用在接觸位置添加節點耦合的方法模擬接觸行為，這種方法基于小變形理論，使部件間連接變得更加簡單[6].

節點耦合就是將有接觸關系的不同部件的網格節點連接，使連接的網格節點在指定坐標方向上的位移取相同數值.

根據節點耦合技術需要建立不同節點間的耦合自由度集，該集合包含一個主自由度和一個或多個其他自由度，在計算時只將主自由度在分析的矩陣方程里進行保存，而將耦合集內的其他自由度刪除.計算的主自由度值將分配到耦合集內的所有其他自由度中[7-8].

一般情況下，對兩個不同節點的所有自由度進行耦合，所需創建的約束方程為

UX(i)-UX(j)+0.1ROTZ(j)=0

UY(i)-UY(j)+0.1ROTZ(j)=0

ROTZ(i)-ROTZ(j)=0

(1)

當對多個節點的自由度進行耦合時，約束方程的通用關系式為

(2)

式中，i為節點的下標號，Ci為自由度系數，ui為節點自由度，C0為常數項.

1.2 響應面法

響應面法就是用一系列基函數來近似隱式極限狀態函數[9-10].多項式響應面基本思想為，通過確定性試驗得到一系列輸入和輸出值，采用最小二乘法擬合多項式函數來近似設計變量和響應值之間的映象關系.

二階響應面(不包含交叉項)的基本形式為

(3)

式中，α0、αi、αii均為待求系數.

寫成向量的形式為

X×α=Y

(4)

把樣本點的值代入式(5)，利用最小二乘法得到系數向量

(5)

1.3 結構可靠性

在實際使用過程中，由于螺栓本身的材料屬性及受載的不確定性，導致其工作強度會發生一定波動，當螺栓的工作強度超過其材料的屈服強度時，就會發生斷裂，無法完成規定的連接功能；當螺栓的工作強度小于材料的屈服強度，則其處于安全狀態，可以繼續工作[11-12].

根據應力-強度干涉理論建立螺栓強度的極限狀態函數

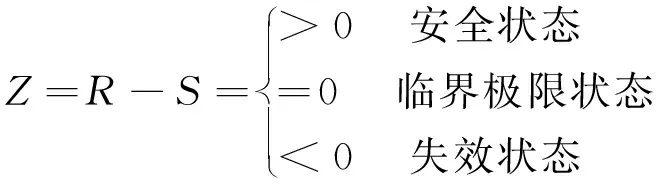
(6)

式中，R為螺栓材料的屈服強度，S為實際工況下螺栓的最大Von. Mises應力.

結構的可靠度就是Z>0的概率.

2 工程案例

2.1 節點耦合模型強度分析

為驗證基于節點耦合技術和響應面法的螺栓強度可靠性分析方法可行性，以地鐵司機室座椅連接螺栓為研究對象，進行螺栓強度可靠性分析.

地鐵司機室座椅有限元模型如圖1～2所示，主要包括頭枕、靠背、座墊、座椅架和底座等結構，座椅通過螺栓與司機室地板連接.

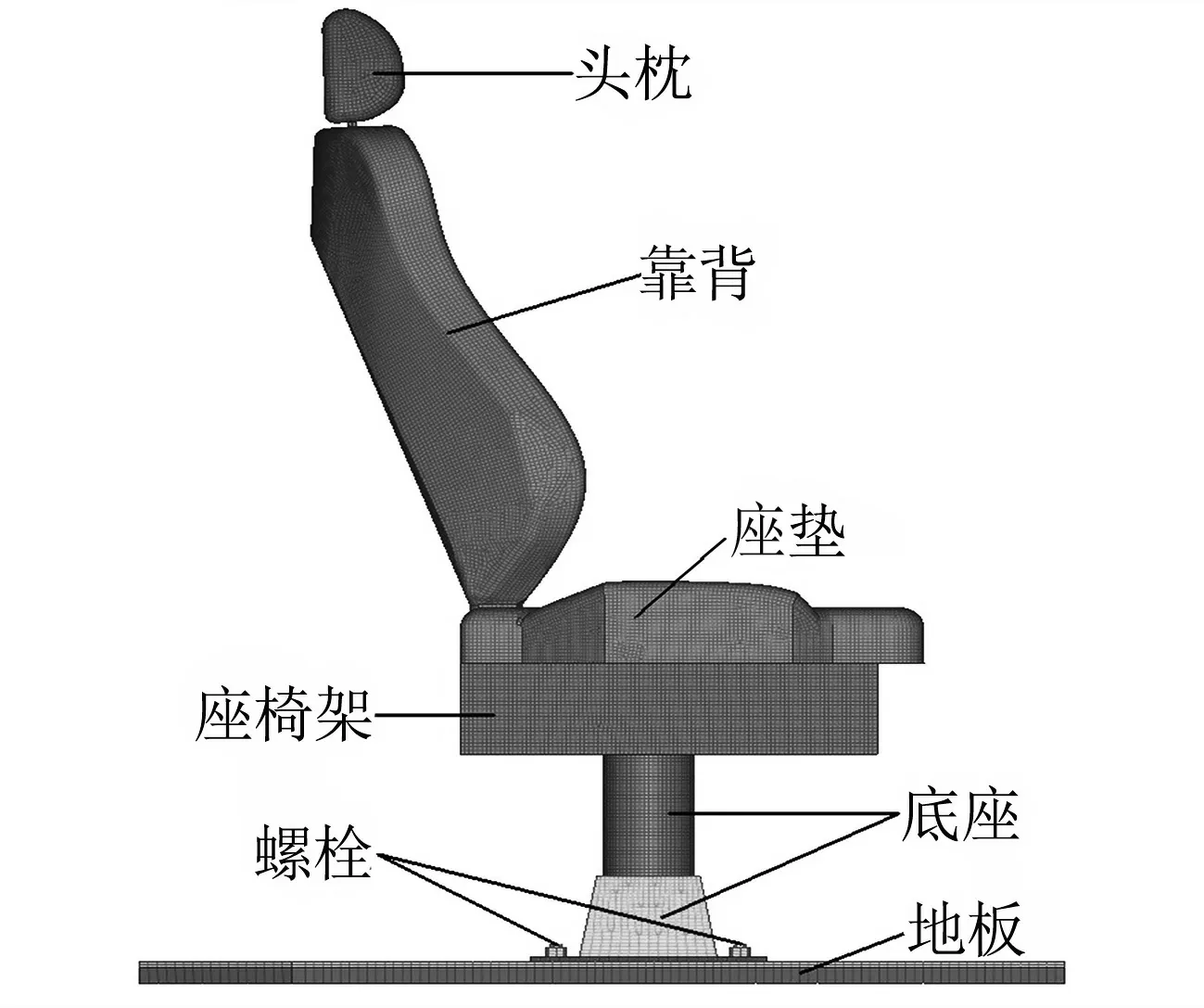
圖1 地鐵司機室座椅有限元模型

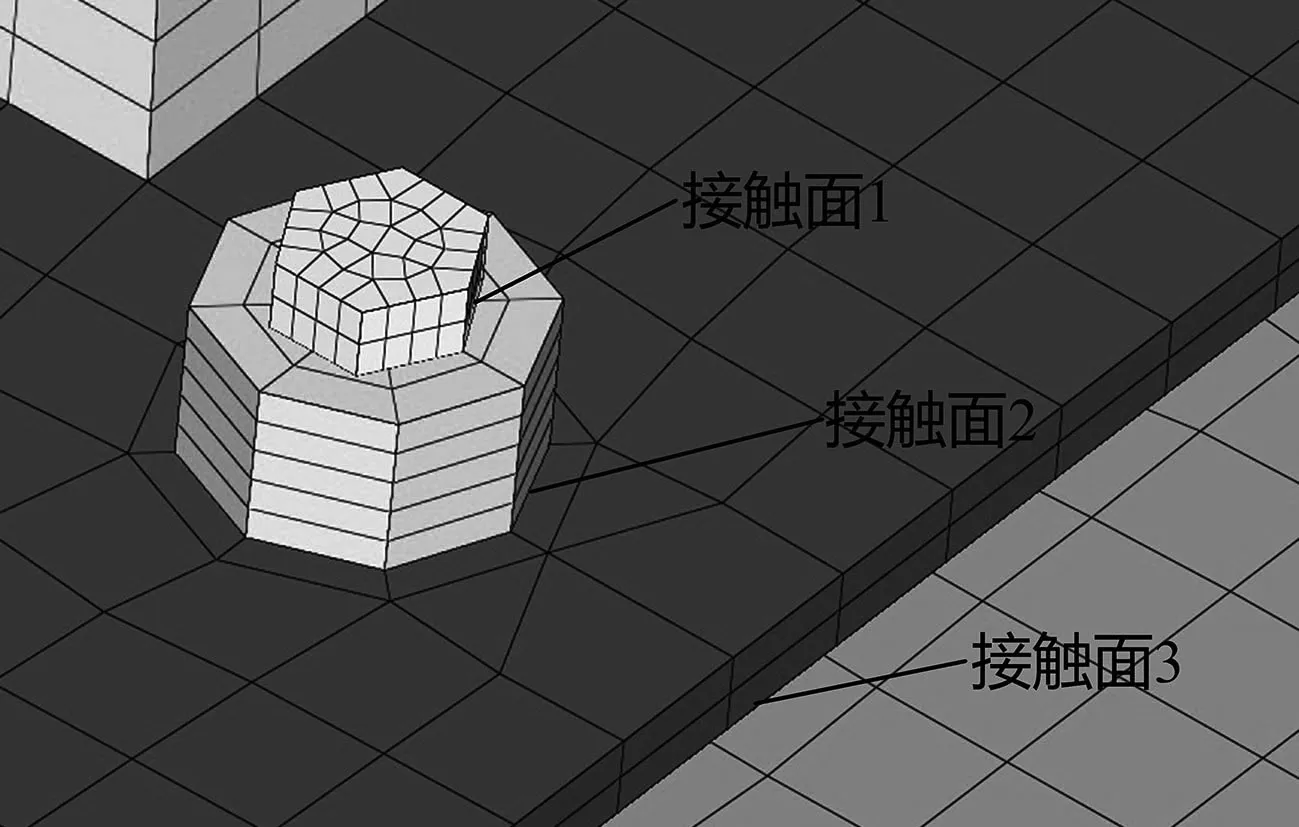
圖2 連接螺栓位置局部放大圖

司機室座椅連接螺栓的靜強度工況包括螺栓預緊力工況和緊急制動工況，其具體工況見表1.

在對接觸區域進行節點耦合建模時，首先根據模型的總體受力和約束情況初步確定節點耦合區域，再根據應力和變形的分布確定耦合節點的范圍，最后根據模型的傳力情況確定主節點、從屬節點和需要耦合的自由度.

基于節點耦合技術對接觸區域進行建模，得到其有限元模型如圖3所示，在螺栓預緊力工況下和緊急制動工況下分別包括13和15個耦合集.對基于節點耦合技術的有限元模型進行線性分析，所得螺栓Von. Mises應力結果如圖3所示.

(a) 螺栓預緊力工況接觸區域有限元模型

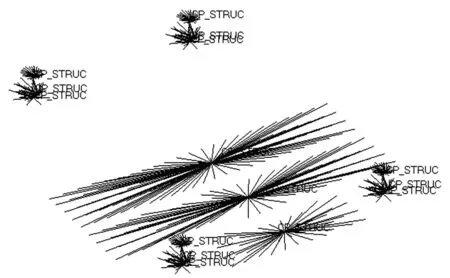
(b) 緊急制動工況接觸區域有限元模型圖3 基于節點耦合技術的接觸區域有限元模型

由圖4可知，在螺栓預緊力工況下，其最大應力出現在螺帽螺桿過渡區域，這是由于節點耦合區域過約束造成的；在緊急制動工況下，螺栓最大應力出現位置為螺桿與地板的連接位置，其分析結果符合工程實際.兩個工況下的螺栓最大Von. Mises應力值為243.63 和538.12 MPa，小于螺栓材料的屈服強度640 MPa，滿足強度要求.

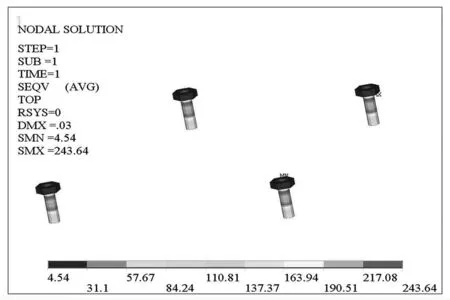
(a) 螺栓預緊力工況螺栓Von.Mises應力云圖

(b) 緊急制動工況螺栓Von.Mises應力云圖圖4 節點耦合模型的螺栓Von. Mises應力云圖

2.2 接觸模型強度分析

對地鐵司機室座椅連接螺栓進行基于MPC接觸算法的非線性分析，并將強度分析結果與節點耦合模型的強度分析結果進行對比，驗證節點耦合模型強度分析結果的正確性.

進行螺栓強度的接觸非線性分析前，為保證強度分析結果的準確性，需要對接觸計算參數進行合理的賦值.按照工程實際經驗，法向懲罰剛度(Normal Penalty Stiffness)和穿透容差(Penetration Tolerance)取0.5，摩擦系數(Friction Coefficient)取0.15，同時打開大變形開關.為加快迭代收斂速度選用牛頓-拉普森迭代法(Full Newton-Raphson).

根據表1中的靜強度工況，對座椅連接螺栓進行接觸非線性分析，得到螺栓預緊力工況和緊急制動工況下的迭代曲線和螺栓Von. Mises應力結果如圖5 ～ 6所示.

由圖5可知，在螺栓預緊力工況下，非線分析迭代到第4步時， 力F，位移U以及轉矩M的范數均低于收斂準則，迭代到第11步時計算結束；在緊急制動工況下分析迭代到第13步時，力F，位移U以及轉矩M的范數均低于收斂準則，迭代到第19步計算結束.兩個工況的非線性分析迭代次數較少，說明分析的非線性程度較低，證明可以考慮采用線性節點耦合技術進行接觸區域建模.

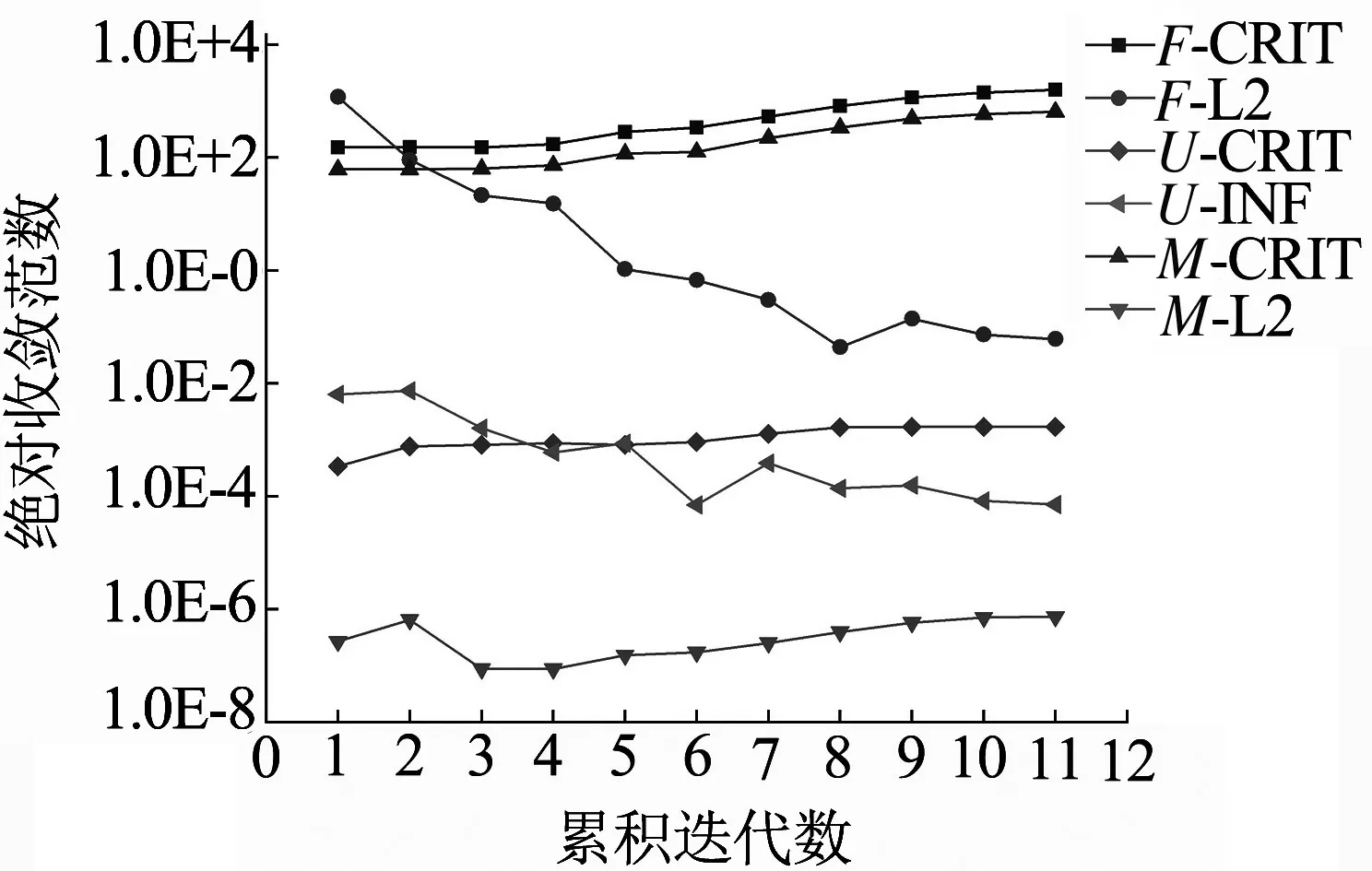
(a) 螺栓預緊力工況迭代曲線圖

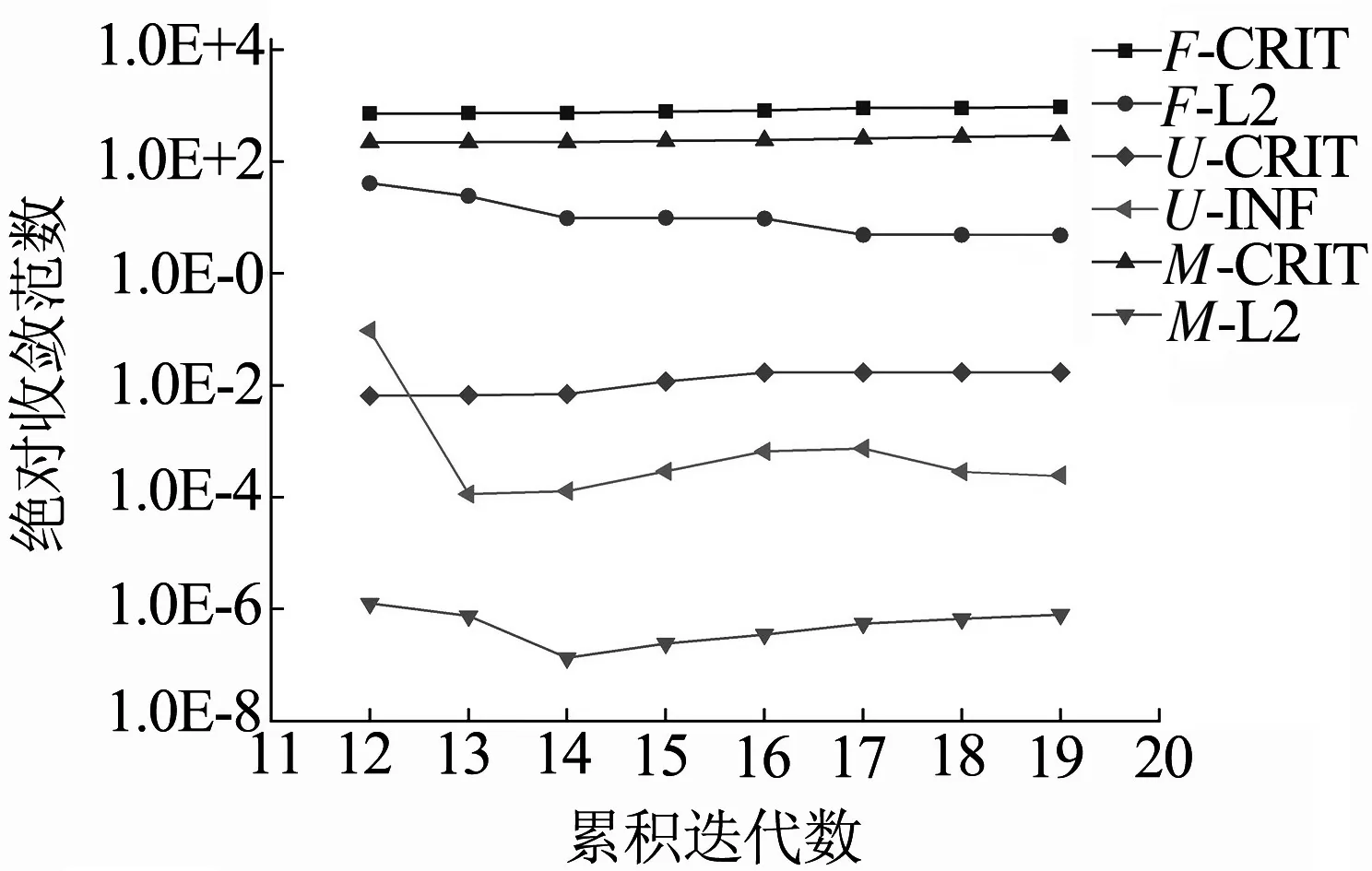
(b) 緊急制動工況迭代曲線圖圖5 非線性分析迭代曲線圖

由圖6可知，在螺栓預緊力工況和緊急制動工況下，螺栓最大應力均出現在螺桿與地板連接位置，說明在螺栓工作過程中螺桿受力較大.螺栓應力值較大的位置存在形狀突變，屬于應力集中高發區，說明分析結果符合工程實際.兩個工況下螺栓最大Von.Mises應力值分別為249.34 和562.55 MPa，小于螺栓材料的屈服強度640 MPa.兩種建模方式和工況下的螺栓最大Von.Mises應力值對比見表2.

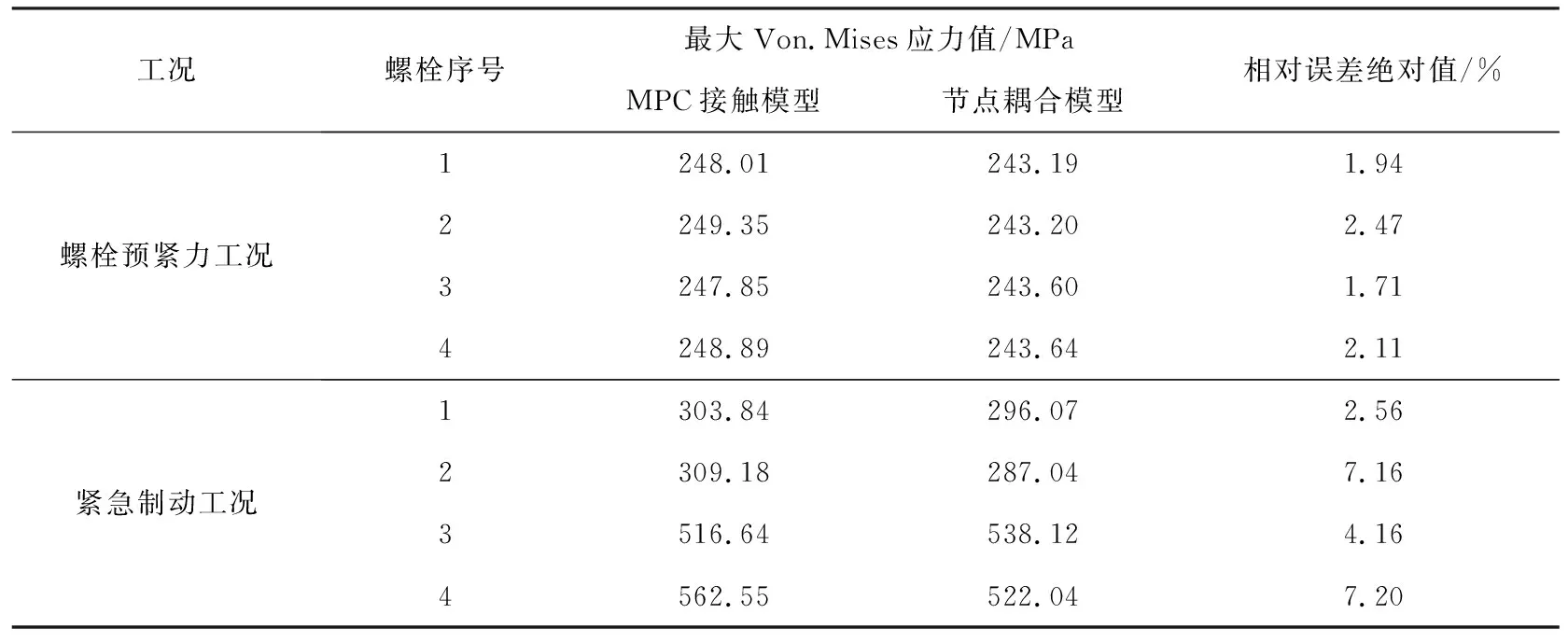
表2 螺栓最大Von.Mises應力值對比

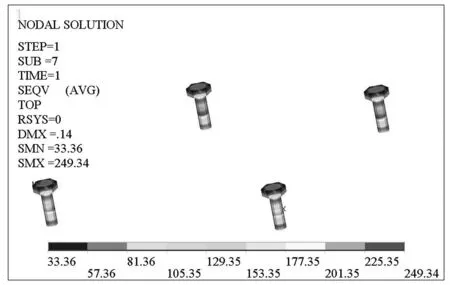
(a)螺栓預緊力工況螺栓Von.Mises應力云圖

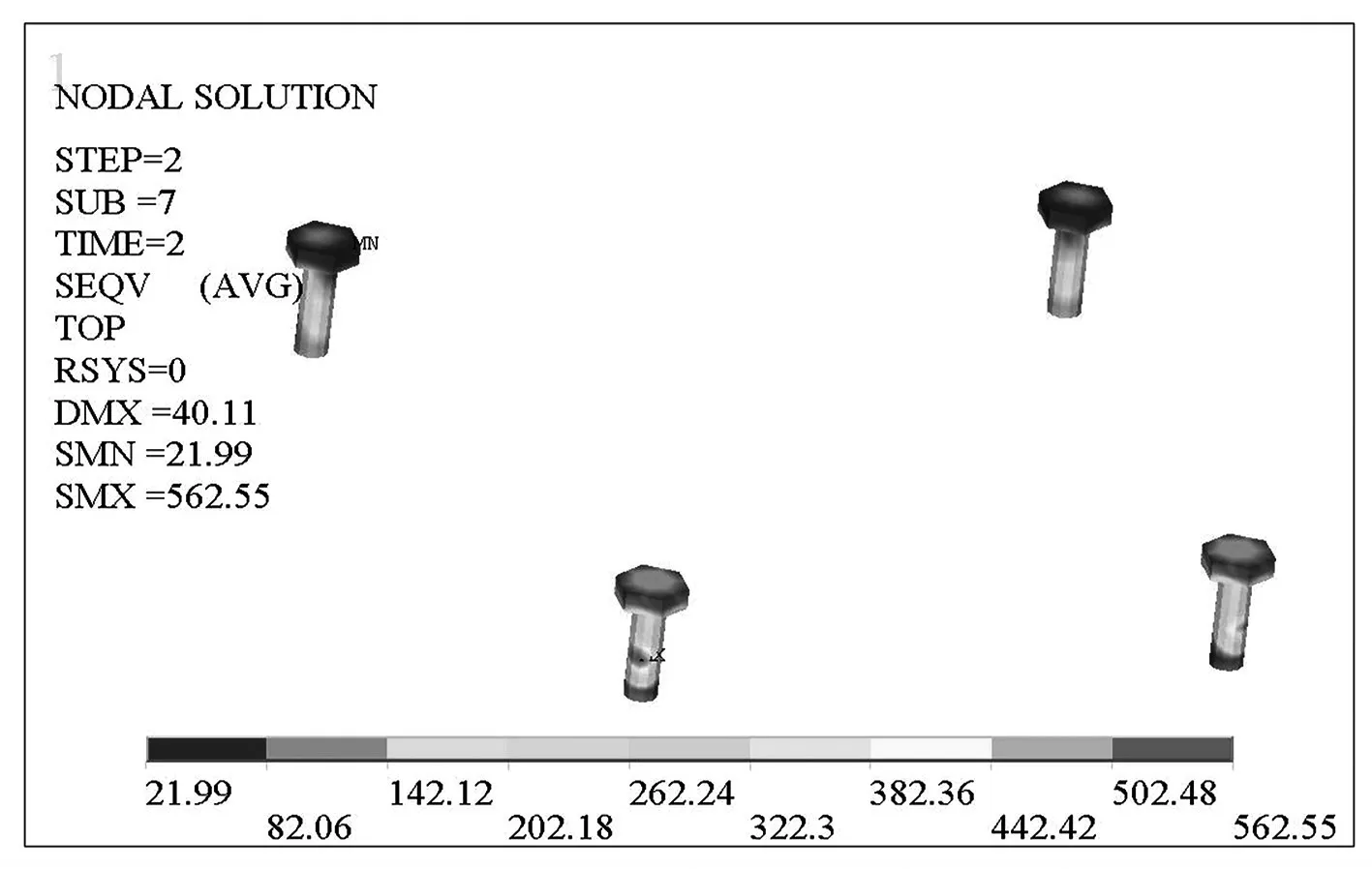
(b)緊急制動工況螺栓Von.Mises應力云圖圖6 接觸模型的螺栓Von.Mises應力云圖

由表2可知，在螺栓預緊力工況下，兩種建模方式下分析所得螺栓最大Von.Mises應力值結果最大相對誤差絕對值為2.47%；在緊急制動工況下，兩種建模方式下分析所得螺栓最大Von.Mises應力值相對誤差絕對值最大值為7.20%，保持在10%以內，證明在滿足一定的計算精度要求的前提下，可以使用節點耦合技術進行接觸區域建模并進行強度分析.

對兩種建模方法下的分析時間進行記錄，發現基于節點耦合技術的線性分析時間僅為接觸非線性分析時間的4.89%.

2.3 螺栓強度可靠性分析

上文已經證明在保證一定計算精度的前提下，可以使用節點耦合技術對接觸區域進行建模，且可以減少大量強度分析時間.為進一步節省可靠性分析所耗時間，在節點耦合技術進行建模的基礎上，采用響應面法代替傳統的蒙特卡羅法進行螺栓強度可靠性分析.

將司機室座椅兩種材料的彈性模量、泊松比、螺栓預緊力以及工作外載作為設計參數，對有限元模型進行參數化，各設計參數以及分布類型見表3.

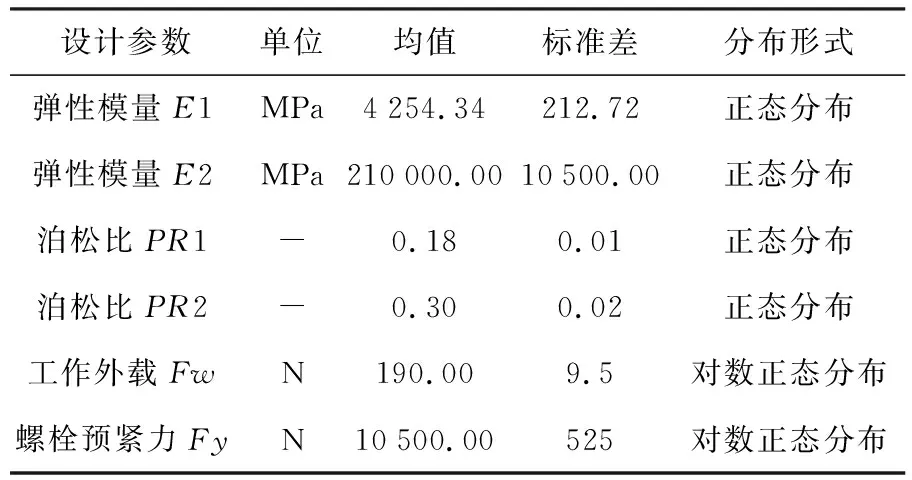
表3 設計參數及分布類型

運用中心復合設計選取初始樣本點，并將其帶入有限元模型中進行確定性分析，得到對應的螺栓最大Von.Mises應力值，試驗設計所得部分樣本點及響應值見表4.

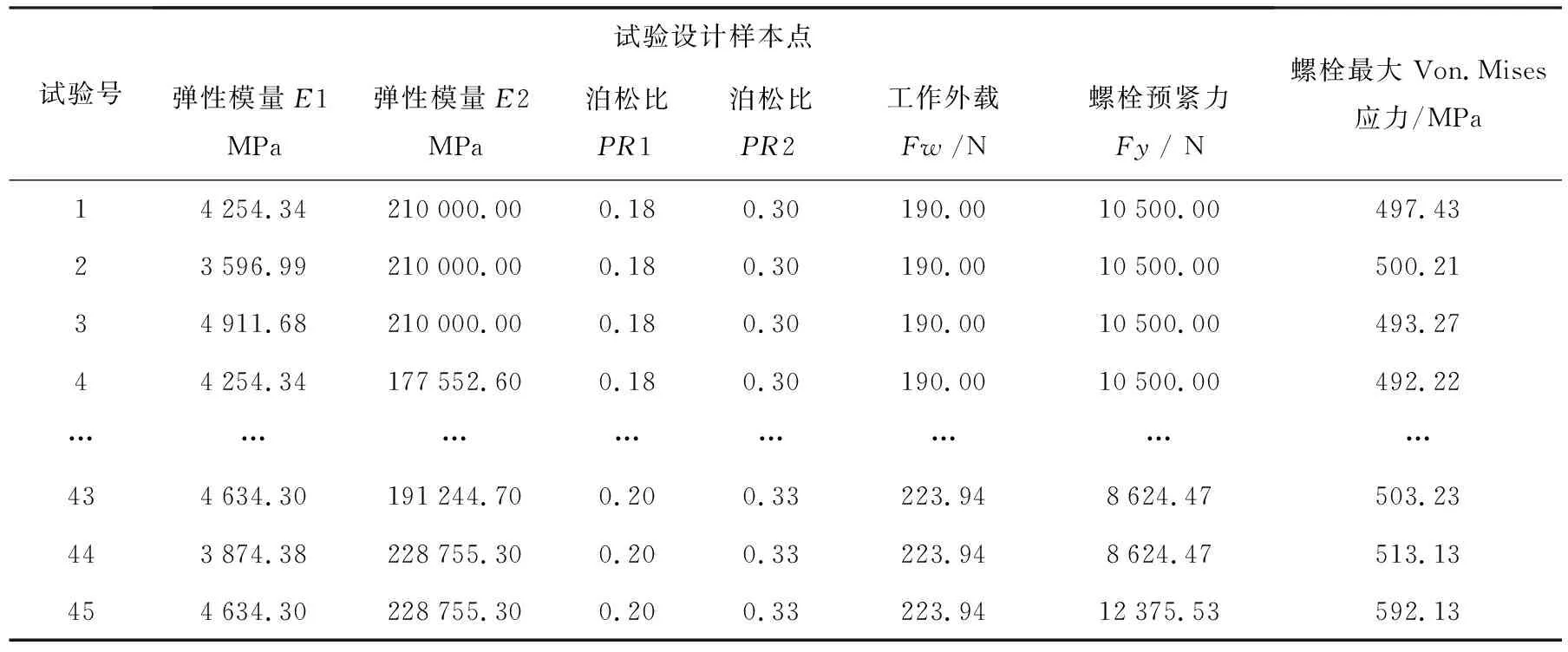
表4 試驗設計及響應值

根據表4的45組樣本點數據，利用最小二乘法擬合二次項系數，建立螺栓強度的多項式響應面函數為

(7)

式中，x1、x2、x3、x4、x5以及x6分別對應彈性模量E1、彈性模量E2、泊松比PR1、泊松比PR2、工作外載Fw以及螺栓預緊力Fy.

各設計參數對螺栓最大Von.Mises應力值的三維響應曲面如圖7所示.

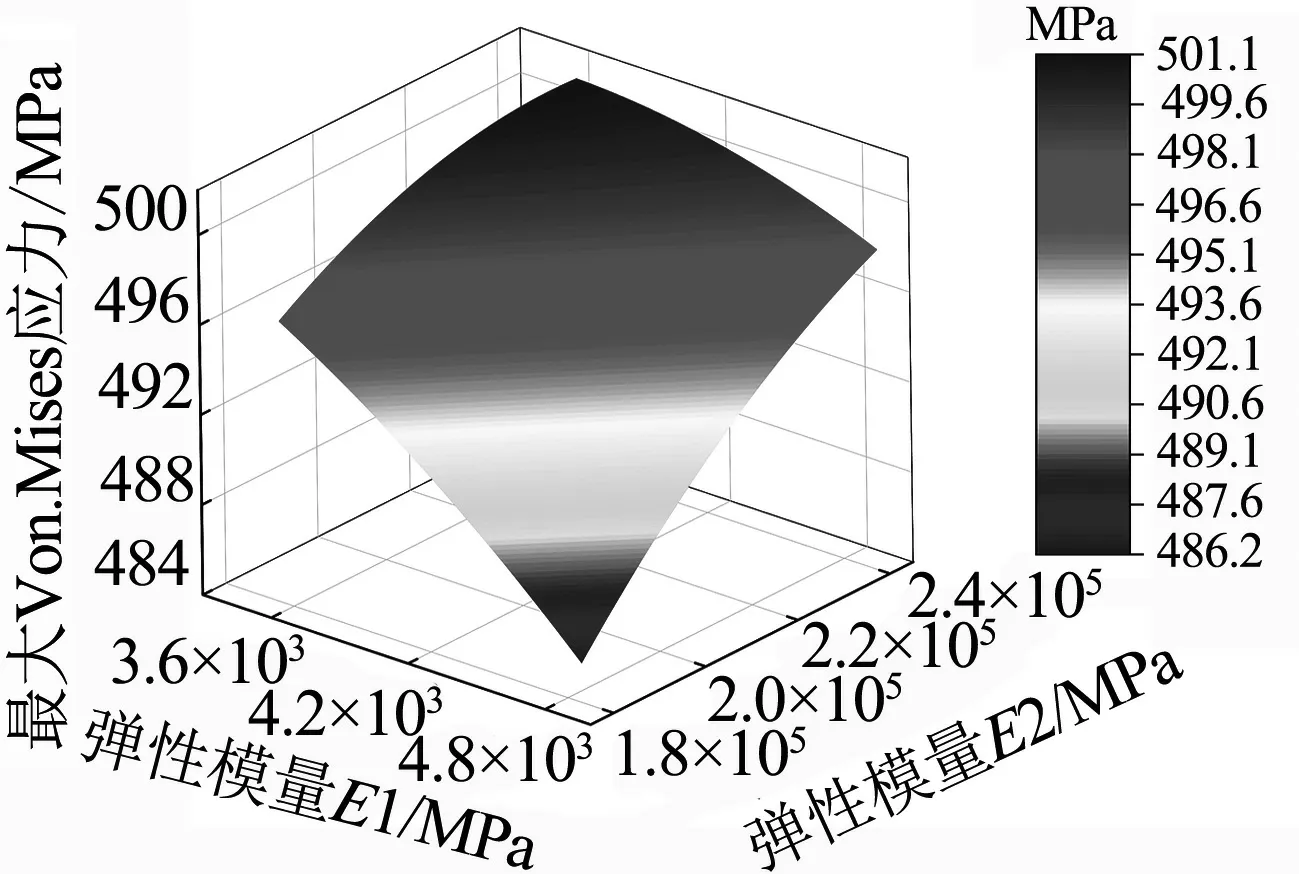
(a)彈性模量E1、E2的響應曲面

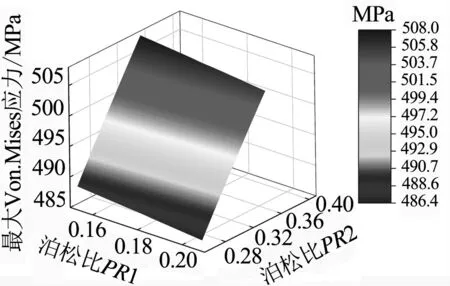
(b)泊松比PR1、PR2的響應曲面

(c)載荷Fw、Fy的響應曲面圖7 設計參數對螺栓最大Von.Mises應力值的響應曲面

由圖7可知，各設計參數的變化對螺栓最大Von.Mises應力值均具有一定影響，彈性模量E1和泊松比PR1的增加會導致螺栓最大Von.Mises應力值的減小，工作外載Fw、螺栓預緊力Fy、彈性模量E2和泊松比PR2的增加會導致螺栓最大Von.Mises應力值的增大，符合工程實際中的情況.工作外載Fw以及螺栓預緊力Fy對螺栓最大Von.Mises應力值的敏感性較強.

運用拉丁超立方抽樣技術進行100 000次抽樣，進行可靠度計算，得到極限狀態函數Z的概率密度以及各設計參數對螺栓強度可靠性的靈敏度水平分別如圖8 ～9所示.

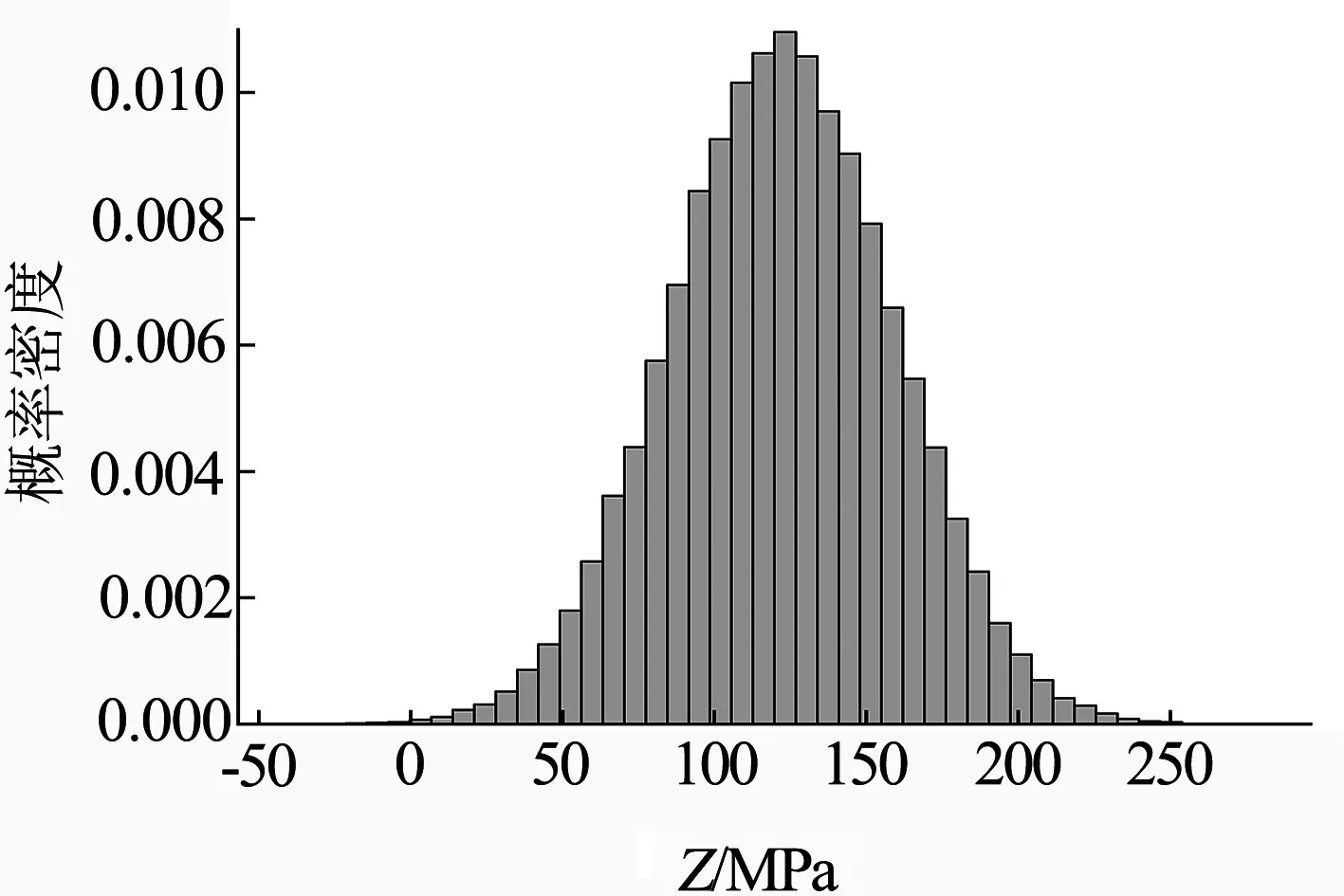
圖8 極限狀態函數Z的概率密度

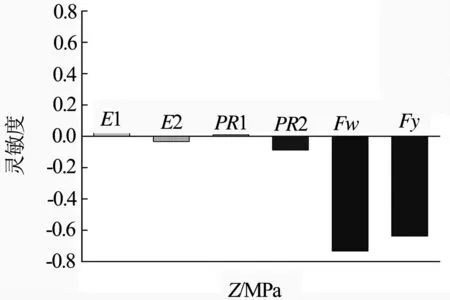
圖9 各設計參數對極限狀態函數Z的靈敏度水平

由圖8可知，極限狀態函數Z的抽樣結果接近正態分布曲線，樣本點落在50 ～200 MPa之間的數量較多.提取可靠性分析結果可得到極限狀態函數Z大于0的可靠度為0.999 6，即螺栓最大Von.Mises應力小于材料屈服強度，結構不會發生失效的概率為99.96 %.

由圖9可知各設計參數對極限狀態函數Z的影響程度.對螺栓強度可靠性影響較大的設計參數為工作外載Fw和螺栓預緊力Fy，且與工作外載和螺栓預緊力成負相關，即螺栓強度可靠性隨著工作外載和螺栓預緊力的增大而減小，與工程實際情況相符.彈性模量E1、彈性模量E2，泊松比PR1以及泊松比PR2對螺栓強度可靠性的影響相對較小，可以忽略不計.螺栓強度可靠性主要受到工作外載和螺栓預緊力的影響，工作外載受現場實況的影響較大，不可控程度高，而螺栓預緊力屬于人工施加，可控程度高，所以可以通過提升螺栓預緊力施加的精確度來保證螺栓強度具有較高的可靠性.

3 結論

(1)基于節點耦合技術對地鐵司機室座椅連接螺栓建模并進行強度分析，解決了基于MPC接觸方法的螺栓強度分析耗時問題;

(2)提出了一種基于節點耦合技術和響應面法的螺栓強度可靠性分析方法，該方法可以在極大程度上節省可靠性分析時間;

(3)可靠性分析結果顯示螺栓結構不會發生失效的概率為99.96 %.由靈敏度結果可知，對螺栓強度可靠性影響最大的設計參數為工作外載Fw和螺栓預緊力Fy.在實際工程中可以通過提高螺栓預緊力施加的精確度來保證螺栓強度具有較高的可靠性.