基于馬爾可夫鏈理論的埋地鋼管內腐蝕狀態預測分析

陳 偉 王友義 嚴俊偉 陳 長

（1.浙江省特種設備科學研究院；2.浙江省特種設備安全檢測技術研究重點實驗室）

管道輸送是油氣工程和市政工程中流體介質最主要的運輸方式。 城市市政管道和油氣管道可在地下延伸數百公里， 由于地質條件復雜，地下管網易受外部環境的損傷，其中管道腐蝕是最常見、最重要的損傷模式。 我國華東地區經濟發達，頻繁的市政建設工程可能使地下管道受到嚴重的第三方破壞，如外保護層破損、陰保失效等。公開發表的文獻中研究管道腐蝕的方法主要包括模糊邏輯理論、阿倫尼烏斯外推法、灰度理論及蒙特卡洛-馬爾可夫理論等。Mohsin K M等基于模糊邏輯理論建立了一種預測保溫層下管道腐蝕狀態的模型，該模型考慮了影響管道腐蝕狀態最關鍵的5種因素（保溫層狀態、保溫層類型、環境因素、管道復雜程度和運行溫度），預測結果顯示，保溫層類型對管道腐蝕狀態影響最顯著［1］。胡松青等基于BP神經網絡理論分析得知影響輸油管道內腐蝕速率的主要因素為介質硫含量和酸值［2］。 Wang H等基于隱藏馬爾可夫理論建立了一種群論方法來預測埋地管道外腐蝕狀態的變化規律，通過對某110 km管道的分析可知，結合該理論與土壤分析、管道內檢測等手段可更精確分析管道整體腐蝕狀態的變化［3，4］。 Ossai C I等通過蒙特卡洛-馬爾可夫理論分析了內腐蝕管道的可靠性并將該理論用于分析某X52鋼管［5，6］。

筆者基于離散馬爾可夫鏈理論建立了管道內腐蝕狀態預測模型，通過漏磁內檢測器和超聲測厚手段獲取了浙江省內某管道的3個檢驗周期內壁厚數據并代入預測模型。

1 管道內腐蝕的離散馬爾可夫模型

檢驗周期中管道的腐蝕時間和腐蝕量皆可當成離散空間變量，即管道的腐蝕過程具有馬爾可夫性。 筆者假設馬爾可夫過程（{Xn，n∈T}）中的參數T（T=1，2，3，…，n）屬于離散時間變量且Xn屬于離散空間集S={i0，i1，i2，i3，…，in}，如果參數n和狀態集合（i0，i1，i2，i3∈S）滿足如下條件［7］：

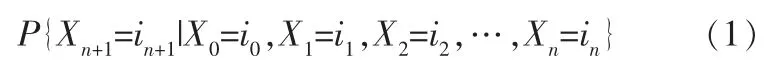
則該馬爾可夫過程{Xn，n∈T}可當成馬爾可夫鏈，且條件概率方程pn（i，j）=P｛Xn+1=j｜Xn=i｝稱為從狀態i到狀態j的一步轉移概率。 其一步轉移概率矩陣為［8］：

對于馬爾可夫鏈，其一步轉移概率矩陣具有如下性質：

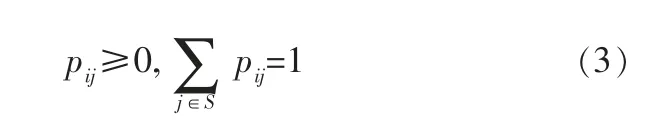
其中，pij=P{Xm+n=j│Xm=i}是條件轉移概率，P（n）=是馬爾可夫鏈的n步轉移概率矩陣，具有如下性質：

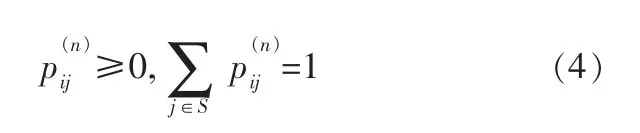
當n≥0且0≤l≤n時，該矩陣具有如下性質：

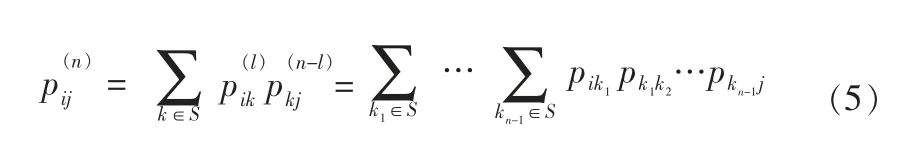
式（5）揭示了n步轉移概率矩陣可由一步轉移概率矩陣定義，將埋地管道腐蝕過程定義為馬爾可夫過程，則轉移概率僅與檢驗時的腐蝕狀態有關而與檢驗時間無關，其初始狀態空間為［9］：

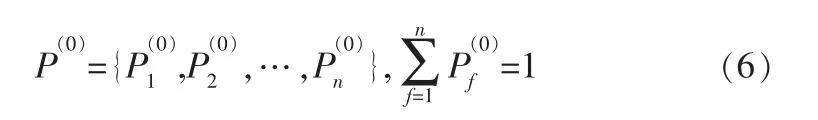
結合實際情形，如果管道的初始狀態p（0）是已知的，則其第n步狀態為：

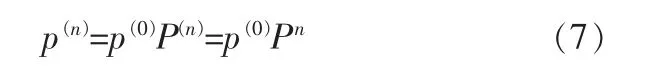
2 管道腐蝕狀態評估流程

通過馬爾可夫鏈評價管道的腐蝕狀態主要包括3個步驟［10］：確定管道腐蝕狀態的壁厚標準；確定管道腐蝕初始狀態并建立腐蝕狀態轉移概率矩陣；確定管道腐蝕過程屬于馬爾可夫過程并預測其腐蝕狀態變化。

2.1 管道腐蝕狀態的壁厚標準

CJJ95—2013《城鎮燃氣埋地鋼質管道腐蝕控制技術規程》依據管道剩余壁厚要求或剩余強度要求將管道腐蝕狀態劃分為7個等級［11］（表1）。 其中Tmin（最小安全壁厚）可通過ASME B31G 獲得［12］。 為了方便評價管道腐蝕狀態，將表1中7種腐蝕狀態等級簡化為5種等級（Ⅰ——輕微腐蝕，Ⅱ——中度腐蝕，Ⅲ——嚴重腐蝕，Ⅳ——非常嚴重腐蝕，Ⅴ——失效），對應的，在馬爾可夫鏈中其狀態向量可表述為K=［1，2，3，4，5］。

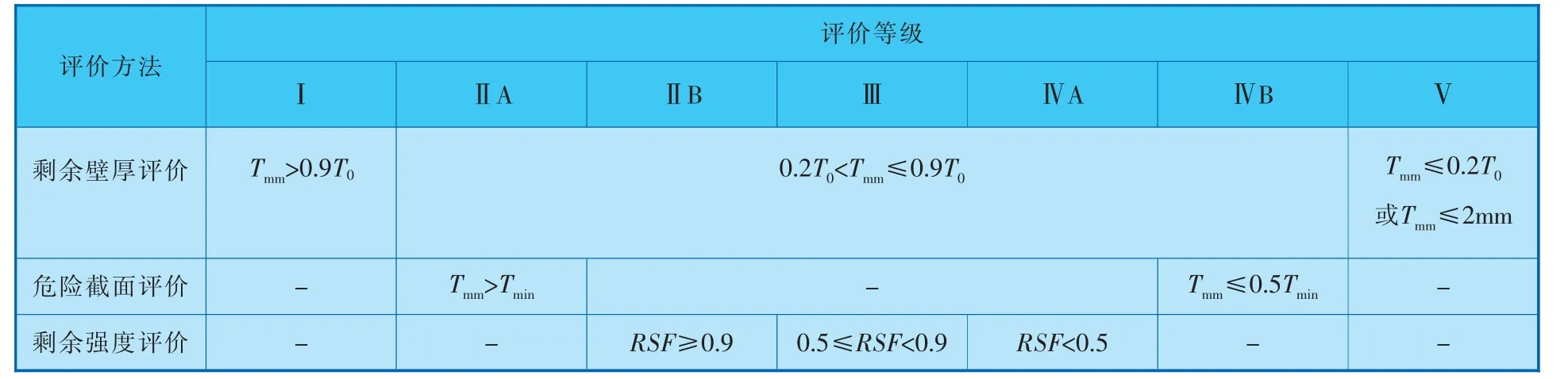
表1 管道腐蝕損傷評價指標

2.2 狀態轉移概率矩陣

當管道腐蝕狀態已確定，可建立相應的狀態轉移概率矩陣。 該矩陣中每個元素皆代表管道狀態處于從“輕微腐蝕”到“失效”的5種狀態中的某一種狀態，典型的狀態轉移概率矩陣如下［13］:

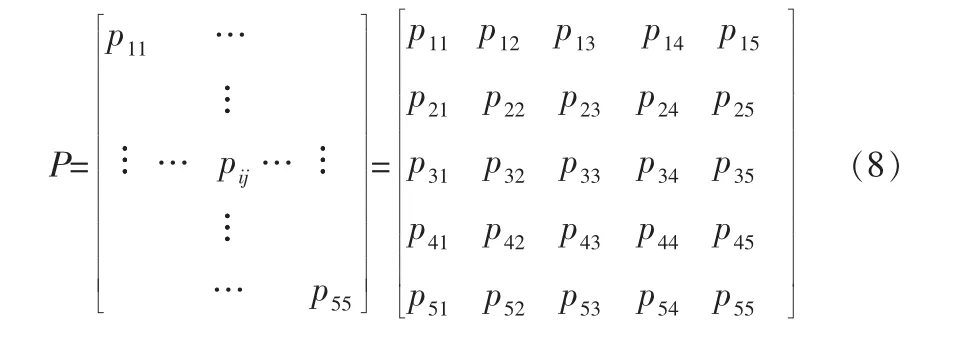
式（8）中的矩陣元素pij代表管道腐蝕狀態從狀態i一步轉移到狀態j的概率，實際情形中由于管壁的腐蝕狀態是不可逆轉的， 不采取補救措施的情形下管道的腐蝕狀態只能更加惡化而不可能逆轉［14］，即當i＞j時，pij=0，因此可將式（8）簡化為：

3 實例分析

選取寧波市至衢州市的管網中某段管道作為分析對象，該段管道長167 km，管道尺寸規格φ406 mm×8 mm。 管道腐蝕狀態具有隨機性，此處選取蝕坑深度最大的位置作為評價對象。 管道服役后第15年進行了第1次基于漏磁技術的內檢測，檢測器示意圖如圖1所示。

圖1 基于漏磁技術的管道內檢測器

檢測器性能參數如下：

凈長度 4 542 mm

凈重 515 kg

最大運行速度 5.5 m/s

最小運行速度 0.3 m/s

檢測里程 167 km

運行時間 34 h

運行壓力 1.5 MPa

運行溫度 0～40 ℃

為了方便內檢測時的收球和發球操作，對管道結構進行改造，增加了收球筒和發球筒的長度并加大端蓋打開角度。 此次檢測發現管道最大腐蝕深度為4 mm。 由于最大腐蝕深度已大于50%管道原始壁厚，因此下次檢驗周期縮短為3年（管道服役后第18年）。

第2次檢驗基于超聲測厚原理， 重點關注前一次檢驗中發現的壁厚最薄的位置。 此次檢驗中測得管道最大腐蝕深度為4.8 mm。

第3次檢驗為管道服役后第20年， 基于超聲測厚原理本次檢驗測得同一位置管壁最大腐蝕深度為5.0 mm，測試現場如圖2所示。

圖2 剝離防腐層后管道本體

簡化后管道腐蝕狀態評價標準見表2。

表2 簡化后管道腐蝕狀態評價標準

最后一次檢驗時測得的管道最大腐蝕深度為5.0 mm，管道剩余壁厚3.0 mm，由表2可知此時管道腐蝕狀態為4（非常嚴重腐蝕），對應腐蝕狀態向量K=［0，0，0，1，0］。一般而言，都認為在外界環境保持基本不變的情形下，管道剩余壁厚隨時間的變化規律符合指數規律，其經驗公式為［15，16］：

式中 a、h——非量綱因子；

t——使用年限，a；

δ——管道剩余壁厚，mm。

將4組檢驗數據（包括t=0，δ=8）代入式（10）并采用最小二乘法進行曲線擬合，可確定式（10）中未知參數：

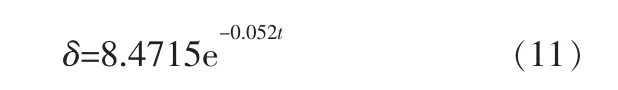
對式（11）中t分別賦值1，2，3，4，5…可確定對應年限的剩余壁厚δ。 結合管道腐蝕狀態評價標準，可獲得不同時期管道腐蝕等級（表3）。

表3顯示了管道腐蝕等級隨使用年限的變化規律，為了使腐蝕等級變化趨勢更明顯，可分別求出不同時期管道最大概率狀態。 文中管道腐蝕狀態為離散時間序列，不同時期管道腐蝕等級的轉移概率矩陣可通過如下所述統計方法獲得。

定義gi為狀態i出現的次數，gij為從狀態i一步轉移到狀態j的次數，pij為從狀態i到狀態j的一步轉移概率，則可得：

根據表3中所列的腐蝕等級可獲得管道腐蝕狀態的一步轉移概率矩陣：

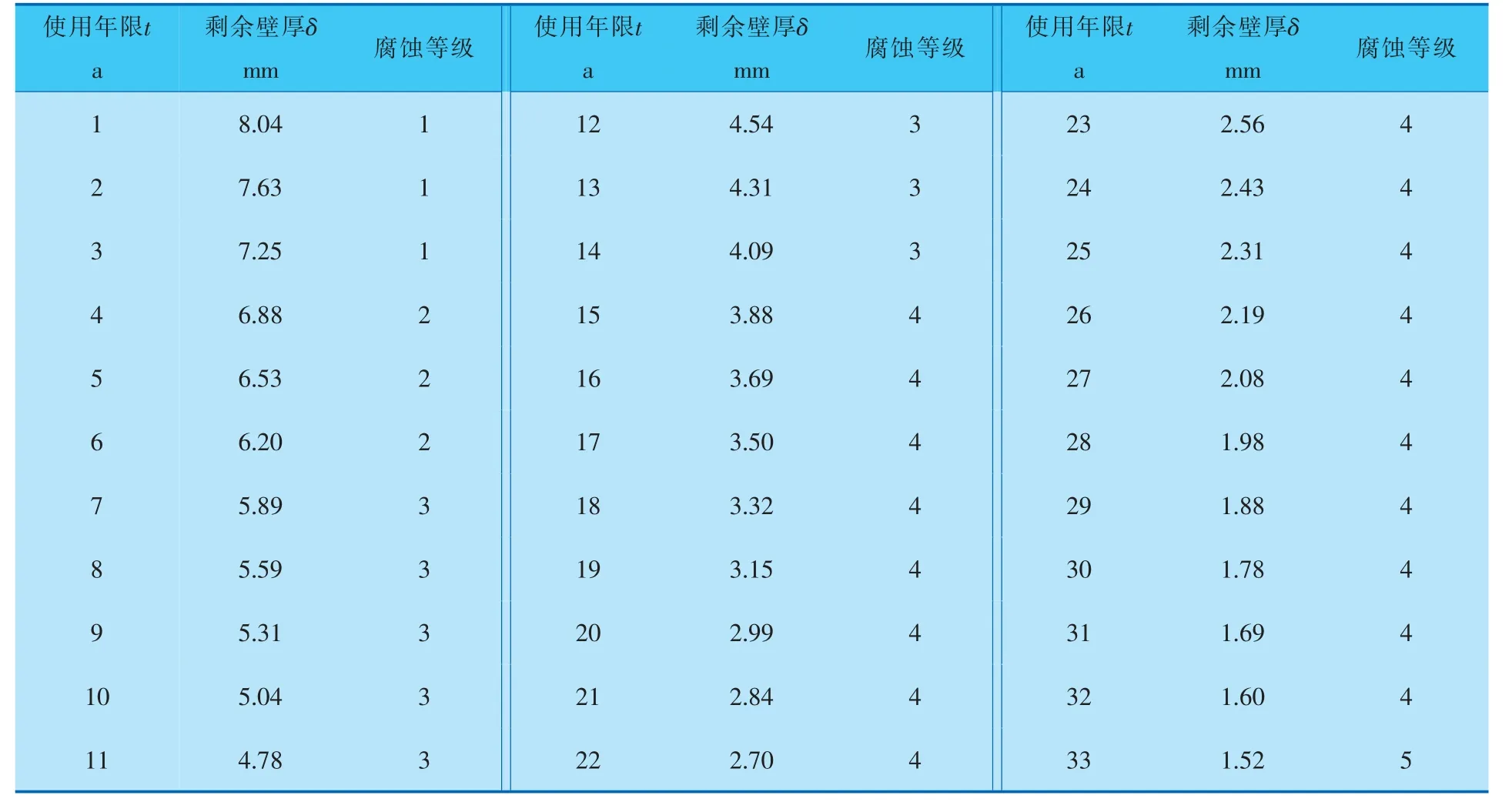
表3 不同時期管道腐蝕等級

此處選取最后一次（第20年）檢驗數據作為初始條件，代入到馬爾可夫鏈中預測管道腐蝕狀態的變化規律。 結合式（4）、（13），可得管道腐蝕狀態預測結果見表4。

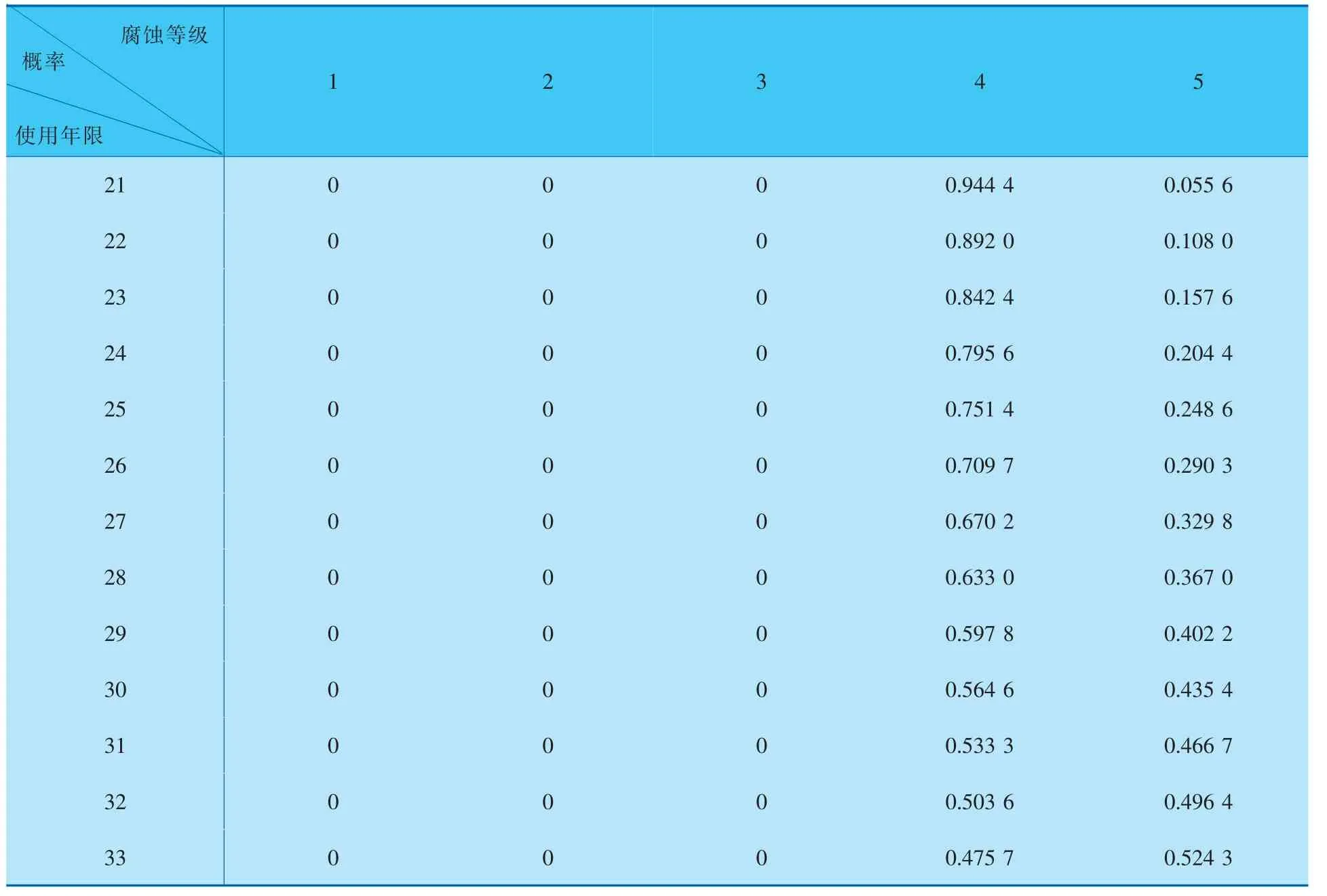
表4 管壁腐蝕等級預測結果

由表4中預測結果可知， 該段管道將在服役33年后失效，該結果與表3中的預測結果相吻合，說明數據量有限的情形下，仍可通過馬爾可夫鏈理論預測管道的腐蝕狀態變化趨勢。 但是該預測結果與“初始狀態”的選取有關，通過計算可知當選取第18年的檢驗數據作為“初始狀態”時，通過馬爾可夫理論預測的管道失效時間為服役后第31年。 若忽略二者之間微小的差距，則采用馬爾可夫鏈理論預測管道腐蝕狀態變化趨勢的優勢仍不可忽略。

由于相鄰兩次檢驗周期之間時間間隔長達數年且現場的工作環境惡劣，同時不同檢驗周期中的檢驗工作可能由不同檢驗單位承擔，導致獲得同一缺陷的連續多次檢驗數據的可操作性較低。 因此目前已公開發表的文獻中涉及到的管道檢驗數據大都為3個或3個以下檢驗周期內獲得的數據。 對于非連續時間周期內的檢驗數據，一種可行的方法是將灰度理論引入馬爾可夫鏈［17］。總體而言，灰度理論是對原始數列進行重新生成操作以使新數列滿足某種已知的分布模型。 例如對于廣泛應用的灰度理論模型GM（1，1），重新生成操作是對原始數列進行一次累加操作（1-AGO）［18］，即：

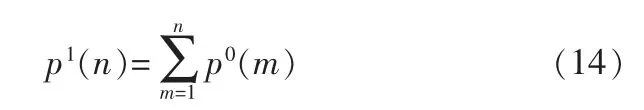
其中，p0（m）為原始數列，p1（n）是新生成的1-AGO數列，此步操作可將任何非負、非擺動數列轉化為遞增數列［19］。 有關灰度理論在非連續檢驗數據中的應用在接下來的研究重點之一。

4 結束語

筆者基于馬爾可夫鏈理論分析了埋地腐蝕狀態的變化趨勢， 結合CJJ95—2013 與ASME B31G確定了以管壁剩余厚度為依據來劃分管道腐蝕狀態。 以某段管道中3組腐蝕數據為例，采用本模型分析了該段管道的腐蝕狀態變化規律。 分析結果顯示，該段管道將在服役33年后因腐蝕失效，盡管該預測結果受預測模型中管道“初始狀態”選取的影響，但仍能反映出該管道的腐蝕狀態隨時間的變化趨勢。 對于非連續的檢驗數據，亦初步探討了引進灰度理論對數據進行處理的可行性，所提出的預測方法和管道腐蝕狀態劃分標準對埋地管道的檢驗工作具有一定指導意義。