時間觸發分布式實時系統容錯時鐘同步算法設計

關博文，朱長昊，張鳳登

（上海理工大學光電信息與計算機工程學院，上海 200093）

0 引言

隨著計算機系統以及大規模集成電路的不斷發展，分布式系統越來越多地應用在人們的日常生活及工業生產中［1-2］。分布式系統從網絡類型上可分為時間觸發（Time Trigger，TT）系統和事件觸發（Event Trigger，ET）系統［3］。事件觸發系統基于事件的發生觸發動作，時間觸發系統基于既定的時刻表或事件調度器的調度，在某個精確時刻觸發動作。為保證系統的實時性以及應對突發事件的魯棒性，通常會同時采用這兩種結構，如FlexRay 與Ethernet 網絡等。從時域上分布式系統又可分為實時系統與非實時系統，實時系統又可進一步分為強實時系統和弱實時系統［4］。本文所研究的是在時間觸發分布式實時系統環境下的時鐘同步算法。

在時間觸發分布式實時系統中，各個節點通常需要大致同時執行某些動作。在這樣的系統中，每個處理器通常都擁有自己的獨立物理時鐘，它們相對于實時都具有一定的偏移率［5-6］。即使讓所有節點的物理時鐘同時啟動，隨著時間的推移，這些節點上的物理時鐘也會偏移實時時間。因此，時鐘必須定期重新同步。在進行設計時鐘同步算法時，不僅要考慮因時鐘老化等物理因素引起的時鐘不同步問題，還要考慮節點的時鐘出現故障或者節點本身出現故障的問題。本文將節點和鏈路故障進行簡化，統一假設為節點的時鐘故障問題［7］。此外，還要容忍系統中的節點為拜占庭將軍問題時的情況。

過去研究中最為經典的是Lamport 等［8］的交互式算法——CNV 算法和交互式一致性算法——COM、CSM 算法。這兩類算法可在任意時鐘故障情況下工作，其中包括出現時鐘拜占庭故障。但是CNV 算法要求出現故障的進程數量不能超過分布式系統總數量的1/3；COM 和CSM 算法雖然能夠在故障節點數量少于總結點數一半的情況下保持時鐘同步，但是需要額外的硬件來提供消息的數字簽名。維也納大學的Kopetz 等［9］分析了CNV 算法并在硬件上測試了該算法；Ramanathan 等［10］、Shin 等［11］提出一種硬件輔助軟件時鐘同步的方法，其軟件同步算法部分借鑒了Lamport 的交互式收斂算法，硬件部分主要實現同步消息的發送和接收，以及記錄同步信息的本地時間戳。最終實驗表明，采用這種軟硬件結合的方法比純軟件同步算法效果更好，精度提高2 個數量級以上，但是增加了經濟上的開銷。在大型分布式系統中，其硬件開銷會成倍增長。

本文提出一種收斂性軟件時鐘同步算法，該算法不需要額外增加硬件開銷，并且它的修正效果相比于容錯中值時鐘同步算法更為明顯。

1 模型設計

1.1 時鐘同步模型建立

在描述本文的容錯性內部時鐘同步算法之前，首先建立一個系統模型，該模型遵循一個寬泛的通用范例［12］，具體就是讀取遠程時鐘技術。讀取遠程時鐘技術分為兩大類：①基于請求回復機制的遠程時鐘讀取技術（Remote clock reading，RCR）［13］，其大體步驟如下：進程pj估算遠程進程pi的時鐘，向pi發送一個請求消息，并等待一段確定的時間來獲取pi的回復；②基于初始同步的時鐘檢測技術（Time Transmission，TT），每輪重復執行同步算法。節點在某個設定的時刻發送包含其時間信息的消息，而不需要先發送時間請求［14］，其代表模型由Lundelius 和Lynch 提出，故通常稱為LL 模型。

由上述文獻可知，基于第一種技術的模型存在的最大估計誤差為2D(1+2ρ)-2(δ-ε)，基于第二種技術的模型最大估計誤差為2(ε+β+ρδ)，其中D 以pj的發送與pi回復這一過程用時的一半為值；ρ是時鐘漂移率；δ是可能的消息延遲范圍中值；ε是消息延遲的不確定度；β是初始時刻節點間的同步程度。

由于時間觸發分布式實時系統是基于時間觸發來發送節點的時間信息，不需要請求回復，因此相較于第一種模型，LL 模型的通信開銷更小。但是相比于第一種模型，因為節點不知道下一條時間消息將由哪個節點發出，所以增加了讀取誤差。但若在非點對點網絡，如廣播式網絡中就不存在該問題。因此，本文采用廣播式通信的LL 模型。LL 模型對重同步周期TP 及節點的初始狀態有一定要求。

1.1.1 基本假設與前提條件

在建立模型并分析算法前，需要對模型做相應假設，同時應用相應的定理以簡化算法的性能分析。

令P 表示系統中節點的集合，由前文可知，其中每一個節點pi∈P 都有一個對應的本地硬件時鐘，用Hpi表示。該時鐘通常由一個晶振和不斷計數增加晶振器節拍的計數器組成。雖然時鐘是離散的，但所有算法都假設時鐘連續運行，如Hpi是一段實時間隔的連續函數。此外，雖然硬件時鐘由于溫度改變和老化會偏離真實時鐘，但通常假設其與真實時間的偏移量在一個很小的范圍內，因此本文做如下假設：

假設1 本地硬件時鐘漂移率假設：存在一個極小的常數ρ >0，定義對任意時刻t，所有硬件時鐘Hpi(t)與ρ的關系如下：

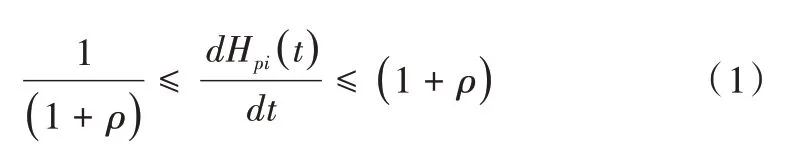
其中，Hpi(t)表示處理器pi 在真實時間t時的本地硬件時鐘值，ρ稱為硬件時鐘的漂移率。該假設表示任一節點的本地硬件時鐘與真實時間的偏差存在一個極小范圍，其上限是ρ，即硬件時鐘的漂移率存在一個合理范圍，若超過該范圍，可能沒有算法能夠將時鐘同步回來。

假設2 通信鏈路全鏈接：節點間通過廣播的方式進行通信，且任一節點pi∈P 在網絡中發送的消息最終都能到達其目的節點，即模型不存在鏈路丟失故障。

在分布式系統中，根據不同的網絡類型以及對網絡負載所作的假設，消息延遲可能或多或少是可預測的［15］。本文假定存在的傳輸（如發送、傳播、接收）延遲的上下限已知。

假設3 傳輸延遲有界：通過任何鏈接發送、傳輸與接收任何消息與真實時間的通信延遲Td存在一個已知的邊界。即：

其中：δ為消息可能延遲范圍的中值，ε為消息延遲的不確定度。當上述假設成立時，時鐘同步算法保證了所有正確的邏輯時鐘間的最大差值在一個范圍內，即精密度γ。這也是確定性算法的顯著特征——通過對通信延遲的上下限做出假設來得到一個定量的精密度值。

假設4 故障節點數有限：時鐘同步算法執行過程中最多存在n個故障節點，其中n是一個正整數。由文獻［16］可知，當系統中故障節點數超過總節點數的1/3 時，在不使用外部數字簽名的技術下，將無法維持時鐘同步。因此，對假設4 進一步假設：系統由m個節點組成，其中的故障節點數為n，它們的關系是：

假設5 算法執行時間：消息延遲除了假設3 中所提的傳輸延遲外，還存在一系列延遲，如任一節點pi∈P在網絡中發送的消息前生成消息所需時間，接收消息后解析消息所需的時間，以及執行同步算法所需的時間。本文假設這些時間都可忽略。通常情況下，造成消息延遲的主要原因是傳輸延遲，而上述的延遲都與節點的處理器有關，簡化起見，將忽略這些延遲。

假設6 初始同步：設T0表示節點時鐘時間的初始時刻表示p節點在初始時刻的真實時間，那么系統中的非故障節點在一開始時是同步在某個固定先驗范圍內的。即：

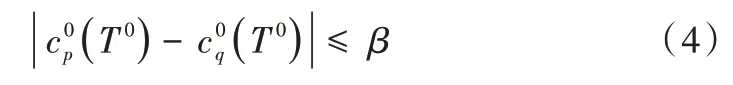
其中為一個定值，p和q為非故障進程。

假設7 同步周期限制條件：為了使同步中非故障節點p發送消息時其余的非故障節點q都與p處于同一輪次，重同步周期TP要滿足以下條件：

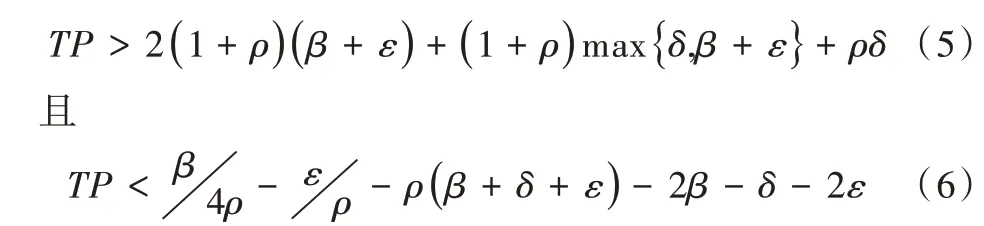
其中，ρ為時鐘漂移率；δ為可能的消息延遲范圍中值，ε為消息延遲的不確定度。β為一先驗常數，表示初始同步程度的上限。

假設8 初始化同步程度限制條件：

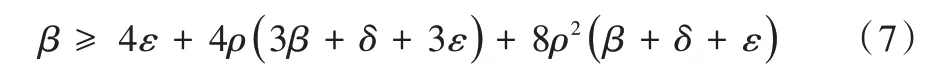
若未特殊指明，本文的其它假設與前提條件都與LL 模型一致［20］。

1.1.2 模型描述

如上述假設及條件所述，系統內節點全鏈接，即可以通過廣播的方式發送消息。算法將在一系列輪次中進行，也就是說，將邏輯時鐘以輪次的形式表示。每輪的時間長度恒定，用L表示，由k個宏時隙組成，其中k＞0。即：

因為每一輪都進行一次時鐘同步，因此其長度也要滿足上述重同步周期條件。每輪要留出固定長度的時間作為修正段，通常稱為NIT 段。在NIT 段內節點執行邏輯時間狀態修正與速率修正，因此在該時間段內通常不執行任何事件。以4 個節點在理想狀態（即完全同步）下為例說明第i輪結構，節點的相關參數如表1 所示。

系統包含一類特殊消息：同步消息Mp，其中p為系統內任一節點。因為采用了上文所述的消息傳輸技術（TT），因此系統的時鐘同步通過時間觸發的方式進行。在輪次i中，i≥0i，每個節點都存在一個互不相同的同步時刻。當本地硬件時鐘達到時就發送同步消息Mp，節點q一旦收到Mp就記下本地時鐘觀測的該時刻

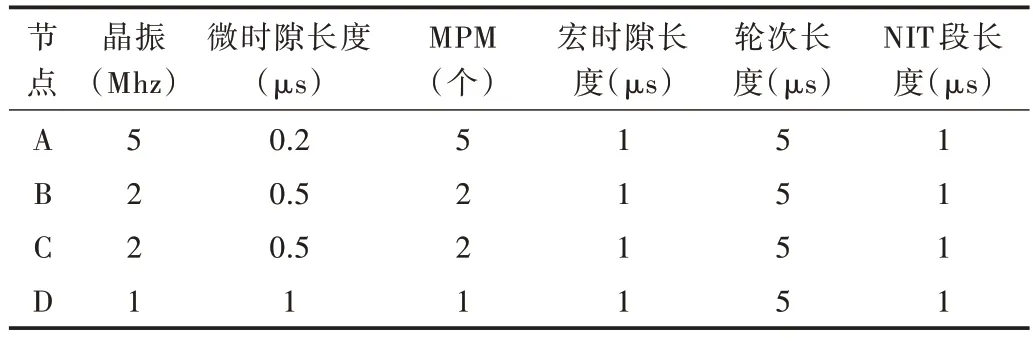
Table 1 Node parameter表1 節點參數

根據表1，各節點第i輪情況如圖1 所示。其中mtj表示節點第j次宏節拍，也就是相應邏輯時鐘的第j個節拍。TNIT表示系統進入NIT 段時的時鐘時刻。系統內各節點的同步時刻都是可知的，即根據不同的網絡和應用需求通過離線設定所得。由可得出在第i輪同步中，節點q觀測的p與q的本地時鐘狀態差，而根據便可得出節點q觀測的p與q的速率差。在得出與各節點的狀態與速率差后，即可應用收斂算法得出修正值，并在NIT 段應用該修正值，完成修正。

Fig.1 State of round i in ideal state圖1 理想狀態下第i 輪狀態

值得注意的是，該結構與FlexRay 十分相似，其原因是FlexRay 同樣也是基于LL 模型，所以準確來說，基于LL 模型的協議都具有相似的結構。同時，FlexRay 分為動態段與靜態段。在靜態段內，節點只能在相應的時隙內發送消息，而本模型則不存在該規則，節點可以在任何時刻發送同步消息。此外，關于為何要將邏輯時間分為輪次的形式也是一個值得探討的問題。究其原因，主要是為了與外部時基進行統一，換言之，系統總是為用戶服務的。而分輪次類似于日常生活中將時間分為年、月、日、分、秒的做法，便于用戶的時間與系統的時間相對應。其次，輪次的結構也便于進行節點間的周期測量，使得節點可以獲得與其它節點的速率差，從而進行速率修正。

1.2 容錯性最值算法

1.2.1 算法提出

基于LL 模型的容錯最值算法思路與LL 模型原始的容錯均值算法類似，不同之處在于容錯最值算法能夠更快完成收斂，使得時鐘間能夠更快達成一致。相應地，其代價是實現的最壞情況下精密度略低于容錯中值算法。

如上文所述，利用收斂函數計算修正項進行容錯時鐘同步的算法，其容錯性的保證實質上在于對修正值的限制。不論是容錯中值算法直觀地對修正項大小進行限制，還是容錯均值算法隱性地在計算過程內部進行限制，都是如此。同樣，容錯最值采用與容錯中值算法類似的對修正值大小進行隱性限制，以保證算法的容錯性，即在故障節點不超過總節點數1/3 的情況下，使得非故障節點的時鐘仍維持在某個精密度下的同步。

1.2.2 算法過程

下面以偽代碼的形式描述第i輪同步中節點q的容錯最值時鐘同步算法過程。

（1）函數及符號定義（見表2）。

Table 2 Pseudocode parameter表2 偽代碼參數

（2）算法描述。

算法：容錯最值算法

輸入：重同步時間

輸出：修正后的節點時鐘值

綜上，通過舍棄掉q節點與其它節點時鐘差值的f個最大值與f個最小值，將余下值中的最大值作為修正值，然后通過修正，實現容錯性內部時鐘同步。容錯最值算法比容錯均值算法少了一個排序的過程，在節點數目較多的情況下可以有效節省計算時間。同時，其收斂速度將快于容錯均值算法與容錯中值算法，這是該算法的顯著特點，但其代價是精密度降低。相對而言，本同步算提供了一種新的思路，在不同場景下使得分布式系統的設計者能夠多一種選擇。

2 實驗驗證

2.1 仿真系統構成

對基于LL 模型的容錯中值時鐘同步算法及容錯最值時鐘同步算法進行仿真實驗，采用專業的現場總線仿真測試工具CANoe 軟件進行仿真測試，從實驗的角度驗證算法理論的正確性。將4 個節點構成一個總線型網絡，網絡中各節點通過廣播方式進行通信。節點1、2、4 為正常節點，節點3 為拜占庭故障節點，即兩面性時鐘節點，其網絡結構如圖2 所示。

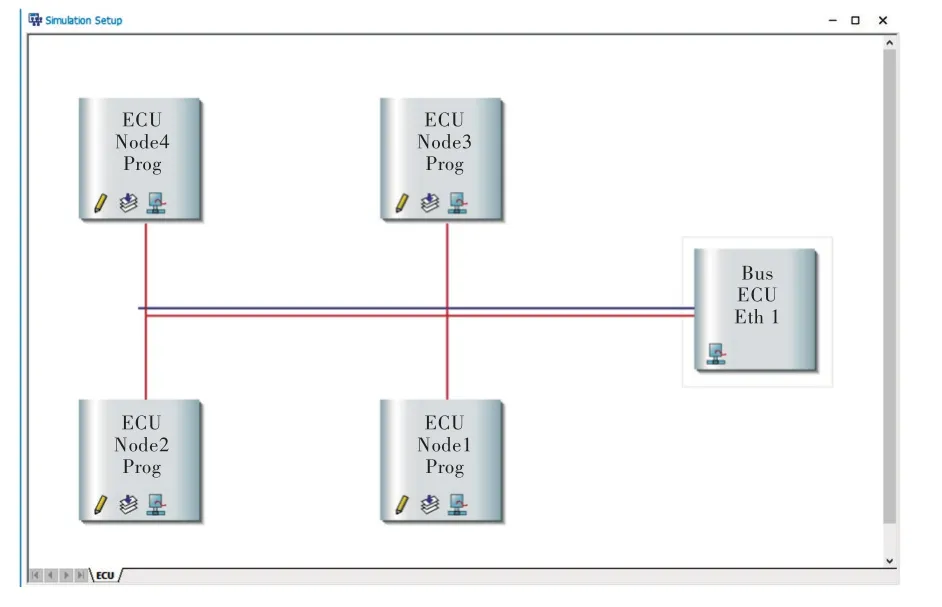
Fig.2 Simulation system network structure圖2 仿真系統網絡結構

實驗中一共有7 條消息，其中4 條是算法相應節點必須發送的同步消息，余下3 條消息用于軟件觀測同步后節點時間差，并非算法所需。同時建立相應的環境變量來表示定時器模擬的節點邏輯時鐘。算法相應的發送接收關系及消息ID 等關系定義見表3。

2.2 仿真系統參數

在搭建好實驗系統網絡框架后，需要確定具體參數。根據之前的研究成果［17-18］及LL 模型的基本約束條件，確定部分系統參數如下：系統容忍的最大漂移率ρ=10-4s，系統內傳輸延遲最大為10×10-6s，最小延遲為5×10-6s，即系統的消息延遲在μs 內［19］。系統內消息延遲不確定度ε=2.5×10-6s，消息延遲范圍的中值δ=7.5×10-6s。根據LL 模型初始同步的基本約束條件式（3），忽略量級過小的參數，在上述條件下系統內初始同步程度βs，因此設系統內初始同步程度β=12×10-6s。再根據LL 模型同步周期的約束條件式（5）及式（6），忽略量級過小的參數，得出系統同步周期TP 的下限量級微秒級，而上限為TPs，即5ms。設系統內每輪同步長度即同步周期TP=0.22ms=220μs，參數如表4 所示。

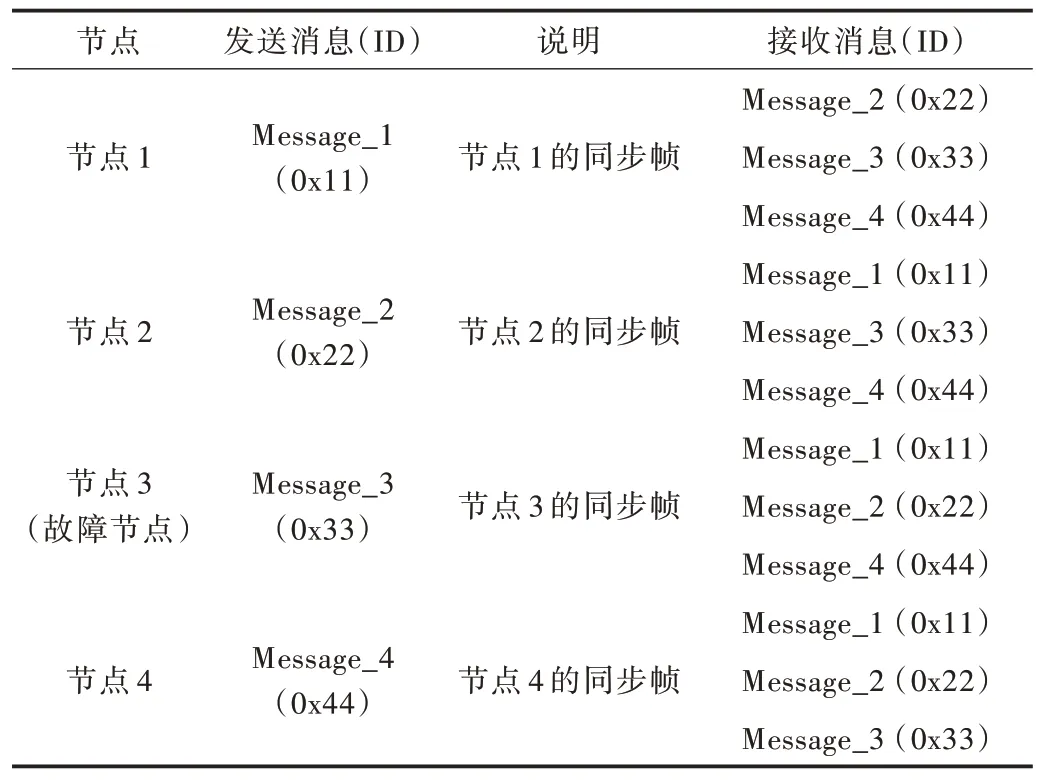
Table 3 Algorithm and message description表3 算法及報文說明

Table 4 System parameter表4 系統參數

根據文獻［20］及前述結論，將表4 中的參數代入精密度計算公式，可得在上述配置下基于LL 模型的容錯中值時鐘同步算法的精密度為：0.014 512 4ms，即14.512 4μs；本文提出的容錯最值時鐘同步算法精密度為0.020 512 4ms，即20.512 4μs。同時根據表4 得節點間的具體參數配置如表5 所示。

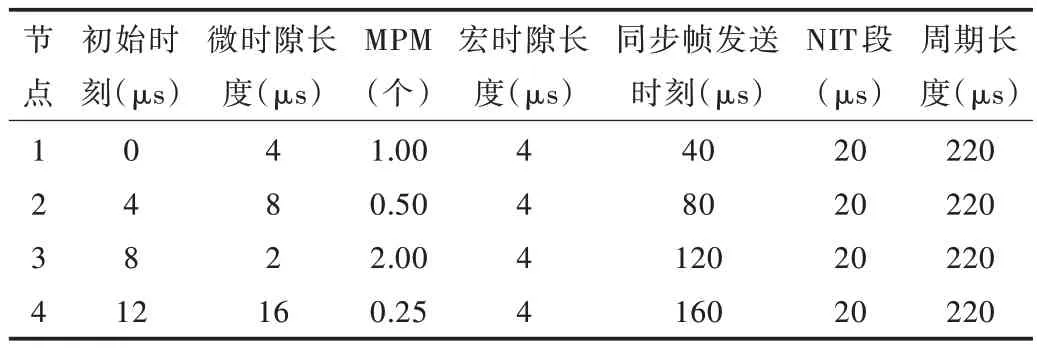
Table 5 Node parameter configuration表5 節點參數配置

2.3 基于LL 模型的容錯中值算法（FTM）仿真結果

根據上述配置搭建系統并運行，使e1、e2、e3、e4 表示節點1 計算的與相應節點的邏輯時鐘差值，而mid為據此得出的中值，Mtick為修正后的單位宏時隙長度，其中節點3為拜占庭故障節點，故e3 的值為隨機值。e12、e13、e14 分別為修正后節點1 與相應節點的邏輯時間差值。而上一輪修正后的理論差值e12、e13、e14 不一定等于本輪測量的實際時鐘差值e2、e3、e4，其原因在于通信延遲的存在。具體修正過程如圖3 所示。

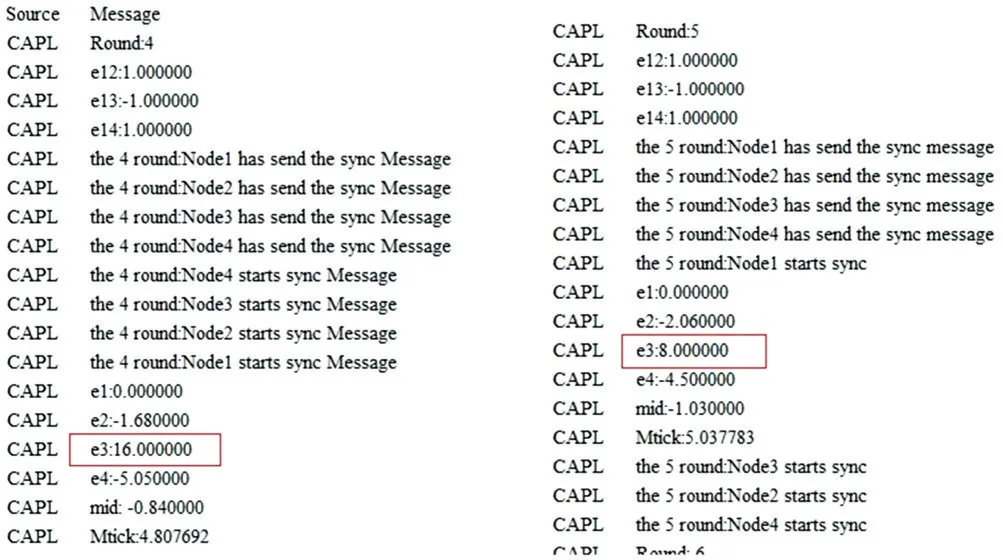
Fig.3 Fault-Tolerant Median（FTM）algorithm correction process圖3 容錯中值算法（FTM）修正過程

詳細結果如圖4（彩圖掃OSID 碼可見，下同）所示，其中兩條紅線分別為以微秒和邏輯時鐘個數為單位表示的FTM 容錯中值算法理論精密度。

Fig.4 Fault-Tolerant Median（FTM）algorithm result圖4 容錯中值算法（FTM）結果

藍色三角實線表示仿真實驗過程中，每輪同步節點1與其它節點邏輯時鐘差值的最大值，單位為微秒；黑色三角虛線表示理論邏輯時鐘差值最大值與實驗邏輯時鐘差值最大值的殘差，單位是微秒；藍色圓點實線表示仿真實驗過程中每輪同步節點1 與其它節點邏輯時鐘差值的最大值，單位為邏輯時鐘的個數；黑色圓點虛線表示理論邏輯時鐘差值最大值與實驗邏輯時鐘差值最大值的殘差，單位為邏輯時鐘的個數。

2.4 基于LL 模型的容錯最值算法仿真結果

同理，根前述配置搭建系統并運行，在注入容錯最值時鐘同步算法到系統中之后，系統節點的邏輯時鐘在任一時間段內的修正過程如圖5 所示。

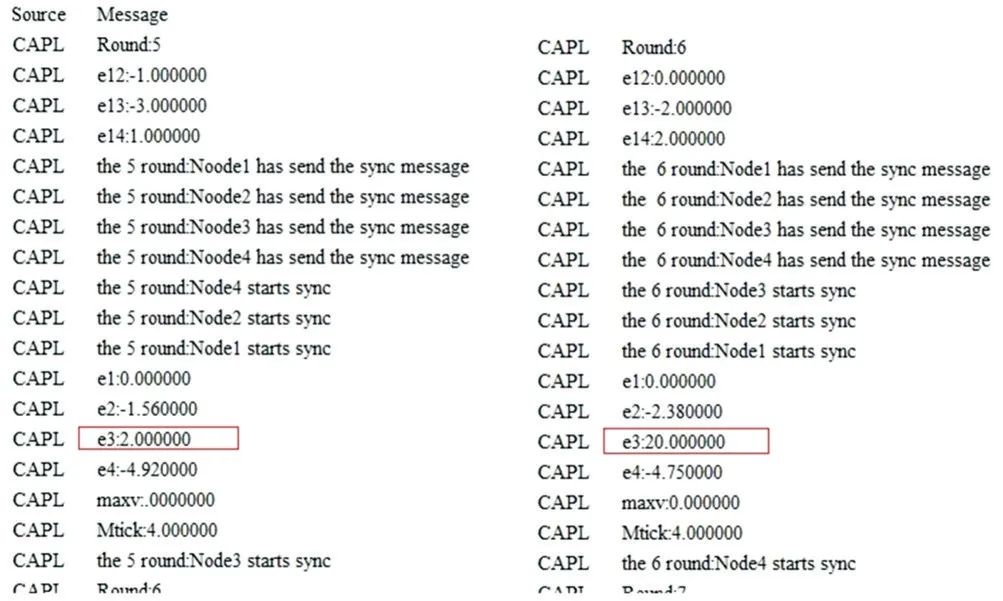
Fig.5 Fault-tolerant maximum value clock synchronization algorithm correction process圖5 容錯最值時鐘同步算法修正過程

其中e1、e2、e3、e4 表示節點1 計算的與相應節點的邏輯時鐘差值，而Maxv 為據此得出的最大值，Mtick為修正后的單位宏時隙長度，其中節點3 為拜占庭故障節點，故e3 的值為隨機值。e12、e13、e14 分別為修正后節點1 與相應節點的邏輯時間差值。而上一輪修正后理論上的差值e12、e13、e14 不一定等于本輪測量的實際時鐘差值e2、e3、e4，原因在于通信延遲的存在。

詳細結果如圖6 所示，其中兩條紅線分別為以微秒和邏輯時鐘個數為單位表示的FTM 容錯中值算法理論精密度。藍色三角實線表示仿真實驗過程中每輪同步節點1 與其它節點邏輯時鐘差值的最大值，單位為微秒；黑色三角虛線表示理論邏輯時鐘差值最大值與實驗邏輯時鐘差值最大值的殘差，單位是微秒；藍色圓點實線表示仿真實驗過程中，每輪同步節點1 與其它節點邏輯時鐘差值的最大值，單位為邏輯時鐘的個數；黑色圓點虛線表示理論邏輯時鐘差值最大值與實驗差值最大值的殘差，單位為邏輯時鐘的個數。

2.5 仿真結果分析

（1）根據容錯中值時鐘同步算法的結果圖可知，本實驗所搭建的系統模型滿足LL 模型的基本條件，其實驗結果完全符合理論結論。容錯中值時鐘同步算法的結果圖符合本文提出的容錯最值時鐘同步算法理論結果，從實驗上證明了本算法的有效性與正確性。

（2）根據容錯中值時鐘同步算法（FTM）修正過程圖與容錯最值時鐘同步算法修正過程圖可知，容錯最值時鐘同步算法的修正過程相比容錯中值時鐘同步算法更為激進，其修正效果更為明顯。同時根據結果圖可知其后果就是精密度的下降。

Fig.6 Fault-tolerant maximum value clock synchronization algorithm results圖6 容錯最值時鐘同步算法結果

（3）根據實驗數據分析發現本文的實驗數據均為整數，究其原因是因為本文實驗計算的結果以邏輯時鐘為單位來表示，因此其最小粒度就是單位邏輯時鐘長度，初始設為4μs。而邏輯時鐘則是用軟件的定時器進行模擬，而軟件定時器用到的最小粒度同樣是整數。由于同一實時時刻不同節點間的時間差就是單位邏輯時鐘長度乘以邏輯時間差值，而單位邏輯時間長度與邏輯時間差都為整數，因此差值也以整數的形式呈現。如果從絕對的完美和嚴謹出發，由于仿真工具及仿真限制的原因，實驗數據結果相當于省去了小數部分，因此并不完全精確。但即便對數據進行向上取整處理，結果仍表明系統中非故障節點的邏輯時鐘差值最大值低于理論精密度，因此該數據仍能證明本算法及觀點的正確性，并不影響得出的結論。

3 結語

本文針對時間觸發分布式系統中的時鐘同步問題，提出了容錯最值算法。基于專業的現場總線仿真測試工具CANoe 軟件進行仿真測試，結果表明，容錯最值算法能有效地同步系統中的故障節點，包括惡劣情況下的拜占庭故障。通過對既往的FTM 算法和本文的容錯最值算法比較可以看出，容錯最值算法的修正效果更為明顯，但代價是同步后的精確度有所下降。本文提供了一種新的思路，使在不同場景下進行分布式系統的設計者能夠多一種選擇。