具有長程相互作用振子環的同步動力學分析

唐智權，朱留華

（1.梧州學院電子信息工程系，廣西梧州，543002；2.玉林師范學院物理與電信工程學院,廣西玉林，537000）

0 引言

復雜網絡作為一種研究復雜系統行之有效的方法，在非線性動力學、生物學、統計力學、現代醫學及工程技術等領域得到了廣泛的應用[1-3]。這些應用主要包含兩方面內容。一方面，一個高度交互的復雜系統可以通過一個圖來恰當的建模，圖中的節點表示動力學單元，連邊表示它們之間的相互作用。從網絡的角度來探究系統的全局特性相對比較容易，例如電網的穩定性、通信系統中數據包的傳播特性；另一方面，研究相應的網絡可為實際系統的操作提供預演，并有助于更好的控制、預測、優化或重構它們。

最近，復雜網絡上的同步引起了科學家們的極大興趣，因為它有助于人們更深刻地理解真實復雜系統的動力學過程的功能和結構[4-5]，例如電力網絡的級聯失效、神經系統中神經元的異常同步。隨著生物網絡和社會網絡的興起,人們對復雜網絡上非線性耦合振子的同步相變進行深入的研究[6-11]。Kuramoto 模型是研究非線性耦合振子同步的經典范例，振子間的同步與否取決于相位差的正弦值與振子固有頻率之間的競爭[12]。

近年來，Kuramoto 模型得到了改進與延伸。一方面，為了獲得理論解析結果，需采用全局耦合；另一方面，為了提高計算效率，需考慮有限范圍或最近鄰耦合。如何調節這一矛盾？在本文中，我們提出了一個按r α-規律衰減的長程耦合策略，其中α≥0 定義了其作用范圍。若α=0 對應于全局均一耦合；α→0 對應于最近鄰耦合。本文的主要目的在于揭示臨界耦合強度對冪律指數α的依賴關系。

1 Kuramoto 模型的變體

本文考慮一個耦合振子環，單個振子的動力學演化滿足下列方程：

式中N是振子總數,θi和ωi分別是第i個振子的瞬時相位和固有頻率，k≥ 0表示系統的耦合強度，固有頻率ωi服從N(0,1)分布，調節冪律指數α可以實現最近鄰耦合和平均場耦合之間的切換。因為周期邊界條件被采納，所以兩個振子之間的距離可表示：

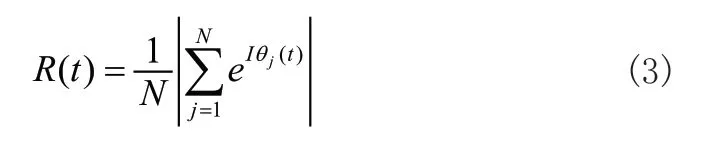
式中為I虛數單位；R(t) ∈ [0,1]，表征系統中振子的相干程度，R(t)的值越大表示想干性越高。R(t)=1意味著系統中振子實現了完全同步。

對于全局均一耦合的情況α=0，耦合強度的臨界值[12]:

式中ω0是固有頻率分布的平均值。接下來我們討論α≠ 0時耦合強度的臨界值。

2 數值模擬與理論分析

圖1 模擬了給定衰減指數α，不同系統尺寸下序參量隨耦合強度增加的變化規律。圖1 顯示：系統的同步特性對系統尺寸不敏感，不同系統尺寸的曲線重疊在一起。對比圖1(a)和(b)發現：臨界耦合強度隨α的增加而增大。

圖1 不同尺寸的系統序參數R 隨耦合強度K 的變化規律。(a)α=0.25,(b)α=0.75

耦合強度未被采用標度變換；(b)耦合強度已被采用標度變換。

圖2 模擬了相同系統尺寸,不同衰減指數α下的序參量隨耦合強度增加的變化規律。圖2(a)顯示：系統的同步特性對衰減指數α有很強的依賴性。圖2（b）顯示橫坐標的適當縮放，使得4 條同步曲線幾乎完全重疊，其中包括平均場曲線。依據這種尺度變換可以很容易地獲得α≠ 0時耦合強度的臨界值：

圖2 不同衰減指數下序參量隨耦合強度的變化規律，其中系統尺寸N=1600

為什么要限定冪律指數的上限？先前的文獻[13]已經證實：當振子數足夠大且α＞ 32時，有限的耦合強度不足以使一維振子環取得全局同步。

如圖3 所示，這種分析解與文獻[14-15]的研究結果吻合的很好，從而有助于我們更好的理解冪律指數對振子環同步動力學行為的影響。

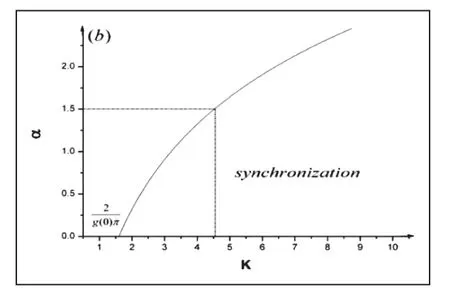
圖3 由方程5 獲得的冪律指數與臨界耦合強度關系曲線

接下來，我們著重討論為什么系統的同步特性對系統尺寸不敏感。文獻[16]指出：在振子環系統中，能量的有限性條件導致了一個共同的修正因子：

研究發現本文模型中的歸一化常數與此處的修正因子是等價的。圖4(a)證實：在誤差允許的范圍內，這兩個因子是可以互換的。為了細致的刻畫它們之間的差異，我們引入相對偏差，其定義式為：

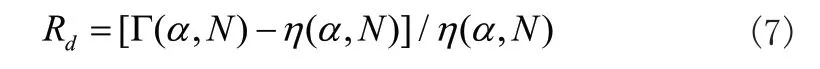
圖4（b）顯示，兩者的相對偏差在α變化的整個區間內均小于4%。歸一化常數與修正因子的等價性，抹平了系統的同步特性對系統尺寸的依賴性。

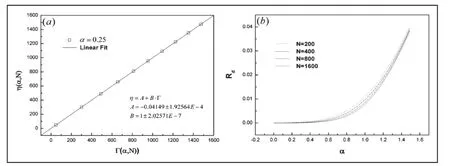
圖4 歸一化常數與修正因子的等價性。(a)歸一化常數與修正因子呈線性關系；(b)相對偏差曲線。

3 結束語

本文利用尺度變換給出了具有長程冪律相互作用的非線性振子環的臨界耦合強度的分析解。研究結果表明：臨界耦合強度雖然對系統尺寸并不敏感，但是對隨距離衰減的冪律指數有很強的依賴性。這為人們研究冪律指數對振子網絡同步動力學行為的影響邁出了第一步。