考慮多類型負荷及風光不確定性的配電網優化規劃
田 浩,王可慶,俞 斌,田文輝,宋長坡,吳肇赟
(1.南京信息工程大學濱江學院,無錫 214105;2.電力系統及發電設備控制和仿真國家重點實驗室(清華大學電機系),北京 100084)
由于一次能源的短缺及越來越嚴重的環境問題,清潔無污染的新能源開始越來越受到重視,并且隨著技術的發展越來越多的分布式電源開始接入到配電網中[1-2]。但是,由于高滲透的分布式電源具有強不確定性的特點,容易使電網產生電壓波動、網損加劇等問題,給電網運行和規劃帶來了極大的挑戰[3]。同時,這些問題也會導致商業負荷、住宅負荷、工業負荷等不同類型的負荷受到影響,即產生了不同程度的負荷波動,從而對配電網的穩定運行造成極大的影響。因此,在進行分布式電源規劃時充分考慮到不同類型負荷的靜態電壓特性具有十分重要的意義。
針對含有分布式電源的配電網規劃,國內外專家學者已經從不同角度進行了大量研究。文獻[4-6]對含有分布式電源的配電網規劃模型及優化方法進行了研究,為后續研究提供了思路與方向。文獻[7]建立了一種基于風電極限場景的兩階段魯棒規劃方法,不僅可以使投資與運行成本最小,還能最大程度降低風電波動對配電網運行的影響。文獻[8]則提出了一種雙層模糊隨機機會約束規劃模型對風電接入配電網進行規劃,規劃過程中將風速處理為一個隨機模糊變量,降低了風電預測的誤差。文獻[9]利用機會約束方法考慮各方面成本建立了光伏并網規劃的多目標模型,并利用混合智能算法進行求解。文獻[10]利用多參數算法改進了傳統的多場景優化方法,對光伏接入電網的容量進行評估,極大地提高了計算效率。但是上述方法在規劃過程中只是考慮了單一分布式電源的配電網接入,與實際中多種分布式電源共同接入配電網存在偏差。
考慮到風電及光伏的優缺點,未來風光互補的配電網規劃將會是重點發展方向。文獻[11]提出了一種基于機會約束規劃的智能軟開關SOP(soft open point)優化配置方法,利用SOP與分布式能源之間的強耦合性規劃運行更靈活可靠的配電網。文獻[12]首先對影響分布式能源的因素進行了變量相關性特征聚類處理,然后建立了收益最大化的多目標規劃模型,并利用帶有精英保留策略的快速非支配多目標優化算法進行了模型的求解。文獻[13-15]通過構建多場景集方法來降低分布式電源的不確定性,并通過雙層規劃模型獲得最優規劃方案。文獻[16-18]在進行分布式電源規劃時,考慮負荷不確定性的影響,利用需求響應特性對負荷進行預測,提高了配電網的穩定性,使得規劃結果更貼合實際應用。
上述研究目標大多集中在降低分布式電源出力的不確定性從而實現其在配電網中最優規劃,但是少有文獻在進行配電網規劃時考慮多種分布式電源情況下不同類型負荷的靜態電壓特性。因此,本文在上述研究的基礎上,考慮分布式電源對負荷的影響,提出了一種考慮多類型負荷分類和風光強不確定性的主動配電網優化規劃設計方法。首先,針對風光出力的強不確定性,在分布式電源出力預測模型的基礎上,通過仿射數原理進一步降低出力的不確定性;其次,考慮到高滲透分布式電源引起的電壓波動會對各類負荷造成不同程度的影響,建立了各類負荷相應的冪函數模型;然后,以網損和電壓波動最小為目標建立了歸一化的數學模型,并利用自適應遺傳算法進行求解;最后,通過算例仿真驗證了本文方法的有效性與可行性。
1 分布式電源及負荷靜態特性電壓模型的建立
合理準確地預測分布式電源的出力是解決其接入配電網規劃問題的基礎。同時,在規劃時還需要考慮分布式電源接入對不同類型負荷的影響。因此,在進行配電網規劃時,需要對各類分布式電源、負荷等重要組成部分進行建模[19]。
1.1 光伏出力預測模型
作為最為常見分布式電源,光伏出力主要受到建設所在地的太陽輻射強度影響。研究發現,太陽光照強度變化符合Beta分布,可表示為
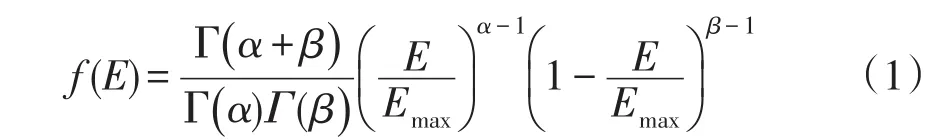
式中:E為太陽輻射強度;Emax為最大太陽輻射強度,可由歷史數據獲得;Γ為Gamma函數;α和 β分別為Beta分布的形狀參數和尺寸參數。
光伏出力與當地的光照輻射強度成正比[20],因此光伏出力可以表示為

式中:PPV為光伏預測出力;S為太陽能電池板面積;τ為太陽能光電轉換效率。
通過對光伏出力的多次預測可以獲得各個時段內預測均值和方差,進而t時段光伏出力區間的上限、下限可表示為

區間數轉換為仿射數需要增加噪聲元標記信息ω[21],假設1個區間數為[x]=[xl,xu],則對應的仿射數為
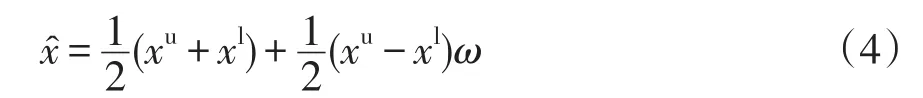
式中,xu、xl分別為所求變量的上限、下限。
因此,利用仿射數進一步降低光伏預測出力的不確定性[22],可表示為
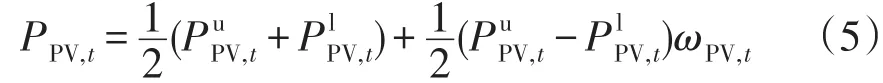
式中,ωPV,t為影響光伏出力不確定性的參數,ωPV,t∈[-1,1]。
1.2 風機出力預測模型
風力發電和光伏發電類似,都是分布式電源中最常見的類型之一。在風力發電系統中,風機出力主要受風速的影響[23]。根據概率學研究發現,風速變化符合Weibull分布,可表示為
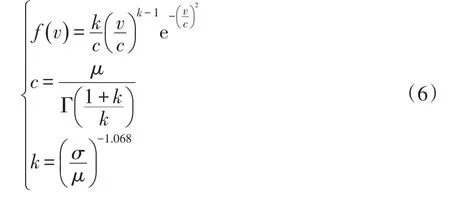
式中:c和k分別為Weibull分布的尺度參數和形狀參數(二者均大于0);σ和 μ分別為其標準差和期望;v為風速。
由于風速具有極強的隨機性,使得風機輸出功率在0至額定功率之間波動。此時,結合風速模型可以將風機出力的數學模型[23]表示為
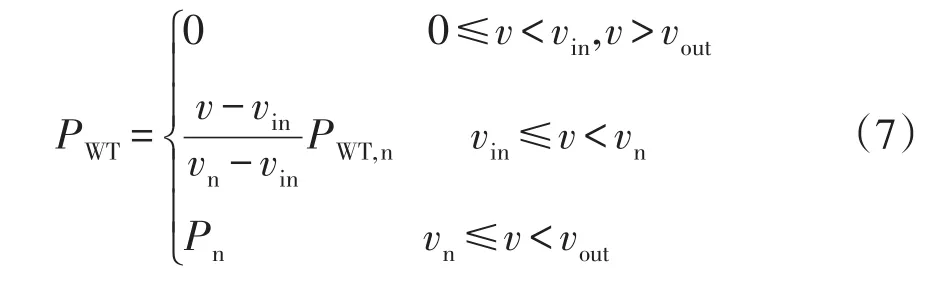
式中:PWT和PWT,n分別為風機出力的有功出力及額定出力;vin、vout和vn分別為風機的切入、切出及額定風速。
與預測光伏出力類似,對風機出力進行多次預測獲得各個時段的預測均值與誤差,則t時段的風機出力的上限、下限可以表示為

同理,根據式(4)可將風機出力變化區間轉換為仿射形式,即
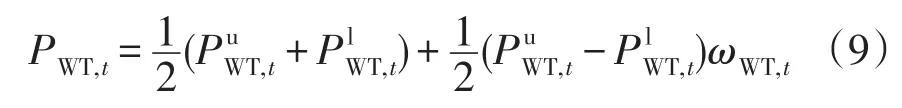
式中,ωWT,t為影響風機出力不確定性的參數,ωWT,t∈[-1,1]。
1.3 各類負荷靜態特性電壓模型
在配電網中,分布式電源的接入會引起電壓波動,而各類負荷的運行工況都是依賴電壓而變化的,并且特性各不相同[24]。因此在進行分布式電源規劃時,考慮負荷靜態電壓特性是很有必要的。
根據行業負荷分類方式,將負荷分為商業負荷、工業負荷、住宅負荷3大類[25]。未接入分布式電源前,系統中整體負荷可表示為
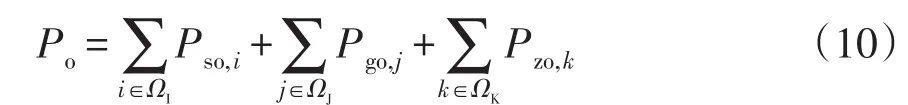
式中:Po為分布式電源接入前配電網整體負荷功率;Pso,i、Pgo,j、Pzo,k分別為整合前節點i的商業負荷功率、節點 j的工業負荷功率、節點k的住宅負荷功率;ΩI、ΩJ、ΩK分別表示各類負荷節點的集合。
負荷功率與其接入母線的電壓和頻率有著一定的函數關系,一般表示為

式中:P為負荷的有功功率;V、f分別為接入負荷母線的電壓和頻率。
對于負荷靜態電壓特性一般可表示為二次型、冪函數兩種形式[26]。考慮到在進行分布式電源規劃時,已經盡可能減少對配電網電壓的影響,在這種情況下冪函數模型相較于二次型模型有著更高的精度。因此,本文選取冪函數模型來表示負荷靜態電壓特性,即
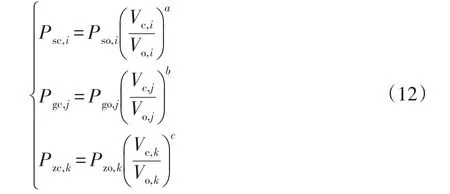
式中:Psc,i、Pgc,j、Pzc,k分別為加入分布式電源后的商業負荷功率、工業負荷功率及住宅負荷功率;Vo,i、Vo,j、Vo,k分別為分布式電源接入前節點i、j、k的原始電壓;Vc,i、Vc,j、Vc,k分別為分布式電源接入后節點i、j、k的電壓;a、b、c分別為各類負荷電壓指數。
同時,文獻[25]給出了不同季節下負荷電壓指數的參考值,如表1所示。
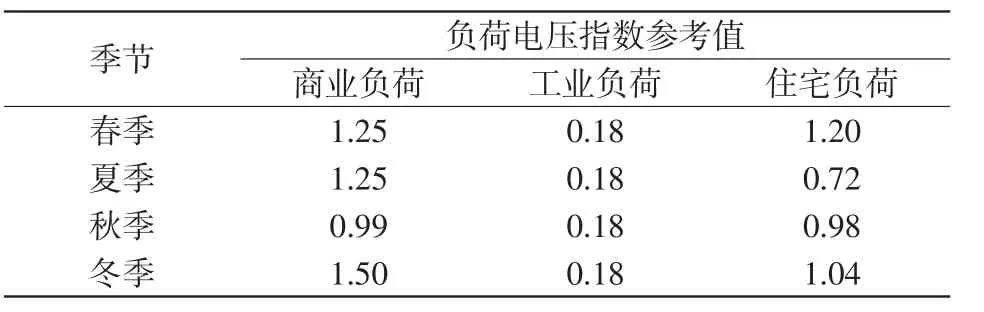
表1 不同季節負荷電壓指數參考值Tab.1 Reference values of load voltage index in different seasons
考慮分布式電源接入后的配電網負荷可表示為
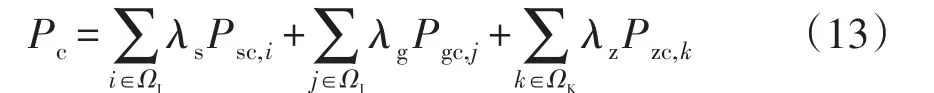
式中:Pc為分布式電源接入后的配電網負荷;λs、λg、λz為其他影響因素造成不同負荷波動的影響系數。
2 計及負荷分類的分布式電源規劃模型
2.1 規劃目標函數
分布式電源由于其不確定性,在接入配電網后,會引起電壓波動和網絡損耗的變化。在分布式電源接入配電網規劃時,為了配電網運行有著更好穩定性,本文以網絡損耗和電壓波動最小為目標函數建立數學模型,可表示為

式中:F為加權處理后的目標函數;F1、F2分別為網絡損耗和電壓波動;ρ1、ρ2分別為可將F1、F2轉換為同一單位的權重系數,二者均大于0,且ρ1+ρ2=1。
本文采用了負荷分類方法,對不同類型的負荷給予不同的權重系數,因而網損可表示為
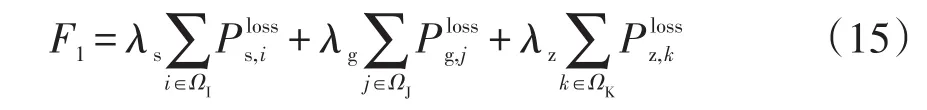
各節點電壓的平均波動率可表示為

式中:Vm和Vnm分別為節點m的當前電壓幅值和額定電壓幅值;ΩM為在配電網中所有節點的集合;M為節點總數。
2.2 約束條件
(1)電壓和電流約束為

(2)功率潮流約束為
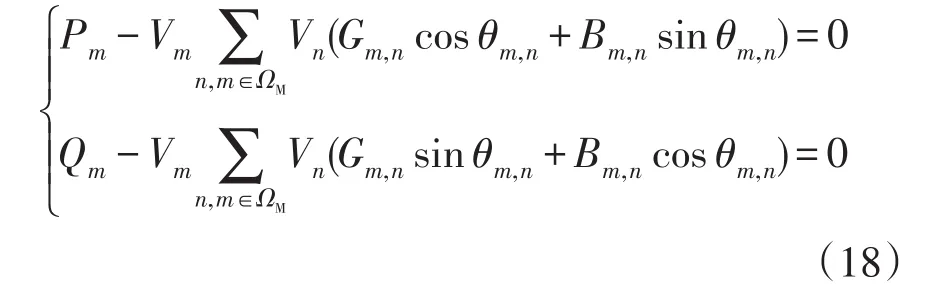
式中:Pm、Qm分別為節點m流過的有功和無功功率;Vn為與節點m直接相連的節點n的電壓;θm,n為節點m與節點n之間的功角;Gm,n、Bm,n分別為節點m與節點n的電導和電納。
(3)分布式電源接入功率約束為
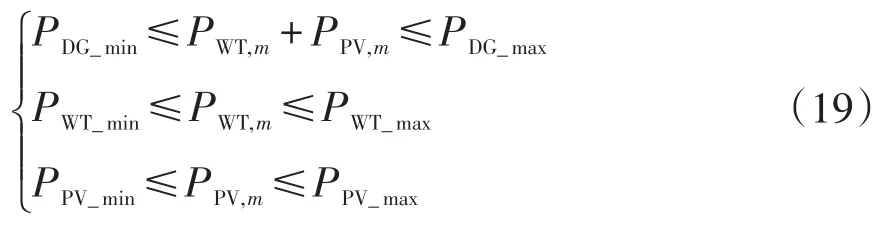
式中:PDG_min、PDG_max分別為配電網允許接入的分布式電源有功功率的最小值和最大值;PWT_min、PWT_max分別為接入配電網的風機出力的最小值和最大值;PPV_min、PPV_max分別為接入配電網的光伏出力的最小值和最大值;PWT,m、PPV,m分別為節點m接入的風機、光伏的當前出力。
2.3 優化求解算法
遺傳算法具有全局尋優能力強、收斂性好等優點,被廣泛應用于復雜的規劃領域[11]。但是,傳統的遺傳算法很大程度上受到交叉率與變異率等參數的影響,使得尋優結果往往不理想。因此,本文采取了自適應遺傳算法AGA(adaptive genetic algo?rithm)進行模型求解。
根據個體適應值調整交叉率和變異率,使得整體進化方向趨近最優解。
交叉率可表示為
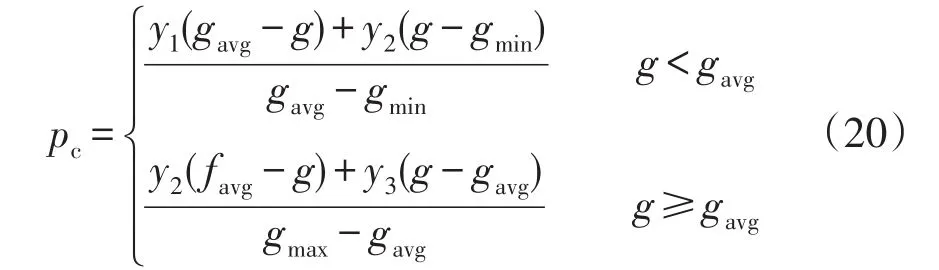
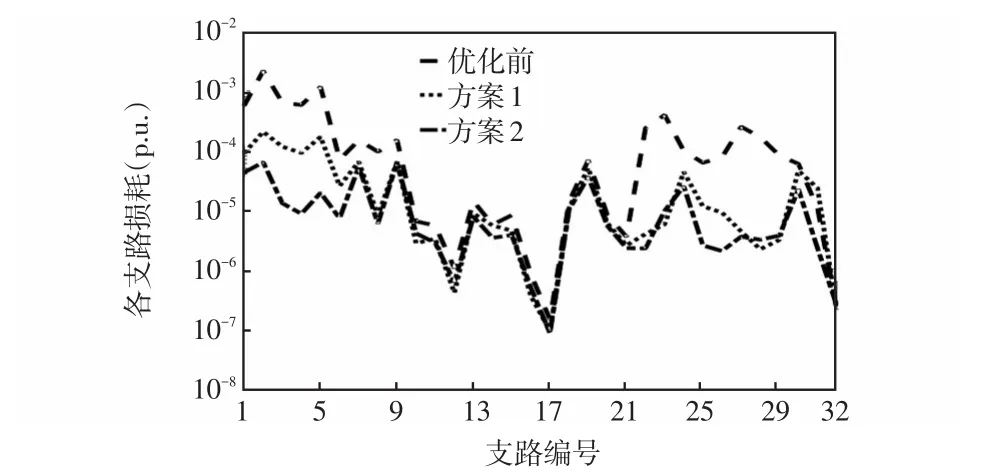
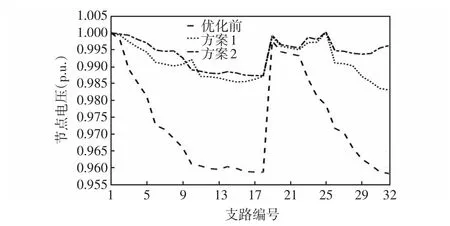
式中:pc為交叉率;y1、y2、y3分別為選定的初始交叉率,且有0 變異率可表示為 式中:pm為變異率;z1、z2、z3分別為選定的初始變異率,且有0 同時,為了保證種群每代的優秀個體會持續保持,當下一代產生的個體中有最佳適應度值小于父代的適應度值時,采用精英保留策略,將父代種群中的最優個體復制隨機替換掉子代種群中適應度值交叉的個體。通過精英保留策略可以保證在迭代過程中所產生的優秀個體不會因為交叉、變異所丟失。 基于AGA求解本文所提出的計及多類型負荷分類和風光強不確定性的主動配電網優化規劃模型,具體求解流程如圖1所示。 圖1 優化流程Fig.1 Flow chart of optimization 為了更好驗證本文方法的有效性,在改進的IEEE-33節點系統(主要表現為各節點負荷分類)上進行了仿真驗證。所采用的IEEE-33節點系統如圖2所示,其他配電網線路的具體參數見文獻[27]。典型日風機及光伏出力如圖3所示。配電網各節點的負荷分類如表2所示。本文所采用的AGA最大種群數設置為100,最大迭代次數設置為200次。出力預測模型考慮風電及光伏出力的時變特性,得出分布式電源在各個時段內預測均值和方差,之后再通過仿射模型進行區間計算,最后獲得完整的結果區間。設定在00:00—05:00及20:00—24:00光伏出力區間的上限和下限均為0。 圖2 改進的IEEE-33節點系統Fig.2 Improved IEEE 33-node system 圖3 典型日風機及光伏預測出力Fig.3 Forecasted output from wind turbine and photovoltaic on typical day 表2 配電網各節點分類Tab.2 Classification of nodes in distribution network 為了更好驗證本文方法的有效性,本文采取了兩種方案進行對比分析:方案1不考慮負荷分類的分布式電源規劃;方案2考慮負荷分類的分布式電源規劃。兩種方案下分布式電源在配電網中的規劃情況如表3所示。從表3可以看出,在進行分布式電源規劃時,考慮負荷分類的影響會改變各類分布式能源的出力比重。這是因為在進行負荷分類之后,晝夜之間的負荷變化差距會更加明顯,各類分布式電源出力相較于未進行負荷分類時有著明顯變化,使得規劃更加符合實際情況。 表3 不同規劃方案對比Tab.3 Comparison among different planning schemes 從整體來看方案2分布式電源的總容量有所減少,即在分布式電源規劃時考慮負荷分類的影響會減少規劃成本。方案1整體網絡損耗為2 591.5 kW,而方案2整體網絡損耗僅有1 042.7 kW,網絡損耗降低了59.76%,也進一步說明了本文方法不僅能夠減少規劃的投資成本,還能夠減少配電網的網絡損耗,極大地提高了配電網運行的經濟效益。 兩種方案下各個支路的網絡損耗如圖4所示。可以看出,兩種方案都能夠很好地減少線路網絡損耗,但是方案2相比于方案1有著更好的優化效果。這是因為在進行分布式電源規劃時考慮負荷分類,會根據不同類型的負荷制定更加詳細的規劃方案,使得規劃結果更加符合不同類型的負荷要求,進而減少各線路損耗。 圖4 不同方案網絡損耗對比Fig.4 Comparison of network loss among different schemes 兩種方案下各節點電壓對比如圖5所示。從圖5可以看出,采用方案2后,各個節點電壓的穩定性相比方案1有了更進一步提升。這是因為進行負荷分類后考慮到不同負荷的靜態特性,在進行規劃時會接入更多無功功率,而這些無功功率會更好地進行電壓調整,進而保證電壓穩定。同時,更小的電壓波動也會為各類負荷提供更加穩定的運行環境,有利于其長期安全運行。 圖5 不同方案節點電壓對比Fig.5 Comparison of nodal voltage among different schemes 針對多種分布式電源強不確定性的特點及對配電網中不同負荷的影響,提出了一種考慮多類型負荷分類和風光強不確定性的主動配電網優化規劃設計方法。針對分布式電源出力的不確定性利用仿射數方法減少不確定性,并在配電網規劃時考慮到不同負荷的靜態特性,建立了各類負荷的冪函數模型,以此減少分布式電源造成的電壓波動對負荷的影響,最后利用AGA進行求解。結論如下。 (1)在進行分布式電源規劃時考慮負荷分類,相比傳統的規劃方法會改變各類負荷的出力占比,使得分布式電源出力更加符合實際。 (2)采用本文方法會增加分布式電源無功出力需求,從而使得配電網的電壓波動更小,系統運行更加穩定。 (3)基于本文方法進行配電網規劃,可以減少分布式電源的規劃成本和配電網的網絡損耗,保證系統運行的經濟性。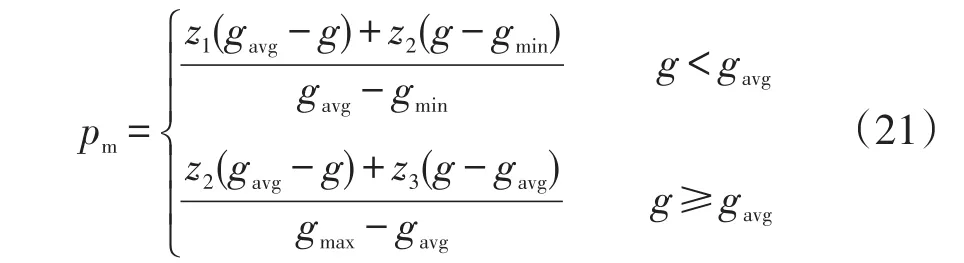
2.4 求解流程
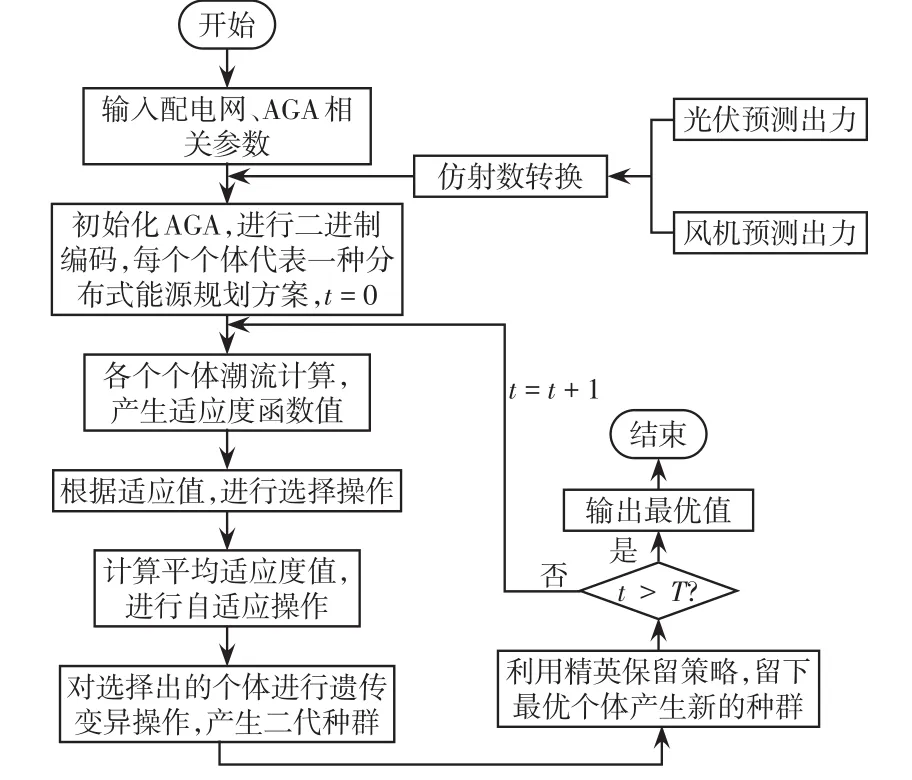
3 仿真分析
3.1 系統參數設置
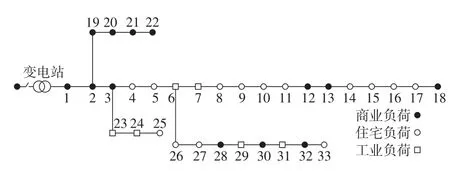
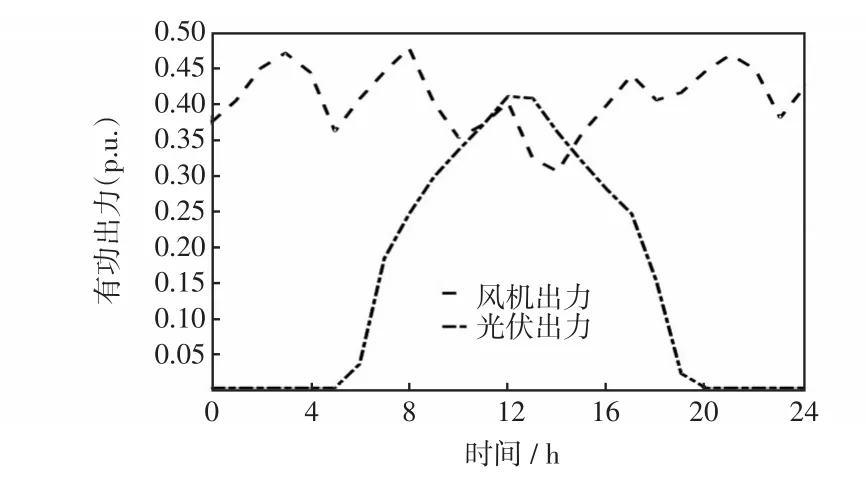
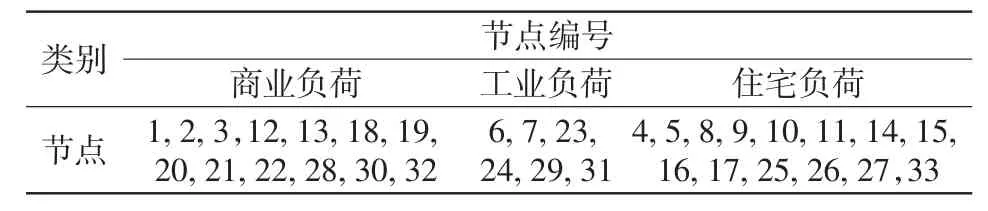
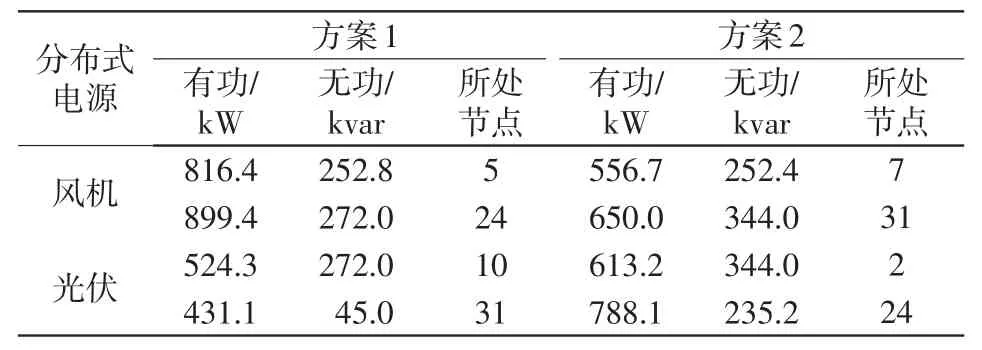
3.2 不同方案對比分析
4 結論

