計及模糊機會約束的電-氣-熱能源樞紐多目標優化調度

李政潔，于 強，龔文杰，張智晟

（1.青島大學電氣工程學院，青島 266071；2.國網青島供電公司，青島 266002）

隨著能源互聯網的發展，能源系統結構發生了很大的變化，各種能源轉換設備技術也得到了進一步發展。在此背景下，融合傳統能源和清潔能源的綜合能源系統IES（integrated energy system）可以使各類能源間的耦合更加密切，使系統運行的經濟性和可靠性提高，因此IES的優化調度成為當前研究的熱門問題。

IES是在某區域內對電-氣-熱-冷等能源進行綜合規劃調度，根據能源間的耦合互補，實現能源的優化配置，從而兼顧系統的經濟性和穩定性。IES的能源轉換和能源儲存設備可以借助能源樞紐EH（energy hub）進行描述。文獻[1]首次提出EH的概念，并介紹了EH的設備及功能。文獻[2]在常規EH模型的基礎上，基于分時電價、分時氣價及經濟性、環保性指標對原模型做了進一步優化，并提出了相應的優化調度策略。文獻[3]考慮了EH的需求響應DR（demand response）策略，將多類型DR負荷納入模型中并展開研究，確定以運行成本最小為目標的運行策略。

在智能用能的背景下，用戶除考慮自身經濟調度外，還可參與電力DR獲取收益，文獻[4]考慮了價格型DR和激勵型DR，建立了一種多時間尺度家庭能量管理系統HMES（home energy management sys?tem）優化模型。綜合需求響應IDR（integrated de?mand response）是在DR的基礎上，引導用戶改變用能方式，通過各類型能源間的需求轉化，實現削峰填谷，加深不同類型能源耦合程度，保證系統可靠運行。文獻[5]首次將IDR定義為DR的延伸擴展，并指出IDR的目標是使用戶消費成本最小、能源供應公司利潤最大。文獻[6]綜合考慮了系統運行成本、碳排放指標和能源利用效率，并構建出IES多目標優化調度模型，給出相應優化策略。

風電出力和負荷預測的不確定性給系統運行帶來了巨大挑戰，對于預測誤差的處理，文獻[7]認定其服從Beta分布，但誤差按特定概率分布太過理想化。也有文獻用模糊參數表示風電出力和負荷[8]，將模型相關約束改進為模糊機會約束進行求解。文獻[9]將含模糊參數的約束條件表示為模糊機會約束，并轉化為清晰等價類求解模型，但文中沒有考慮負荷的模糊性。

隨著IES技術的進步和風力發電的發展，能源間耦合更加密切，經濟調度和環保指標成為了系統運行過程中需要考慮的重要問題。基于此，本文計及IDR，以模糊參數表示風電出力和負荷預測，建立了考慮模糊機會約束的EH多目標優化調度模型：將模糊機會約束轉化為清晰等價類，結合分群渦流搜索算法對模型進行求解。

1 IES模型

IES包括能源供應側、能源轉換、儲存設備及負荷側。

1.1 能源樞紐

EH是多種能源轉換、儲存設備的集合，在接收來自輸入端的各類型能源后，經能源轉換設備實現各類能源間轉換，由輸出端口向負荷側供給能量。當能量供應不足或尤有余量時，EH中能量存儲設備會補足或接收額外的能量。

EH的輸入輸出是線性關系，可由線性能源耦合矩陣表示[10]，即

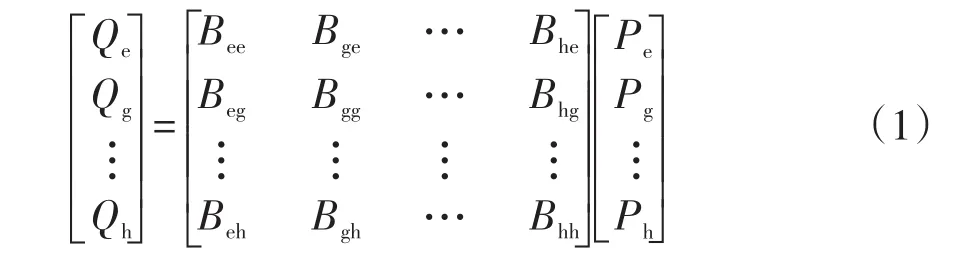
式（1）可簡化為

式中：Qe、Qg、Qh分別為EH的電、氣、熱功率輸出；B為耦合因子，表示EH的輸入與輸出間的轉換系數；Pe、Pg、Ph分別為EH輸入端的電、氣、熱功率。

本文建立的EH模型如圖1所示。

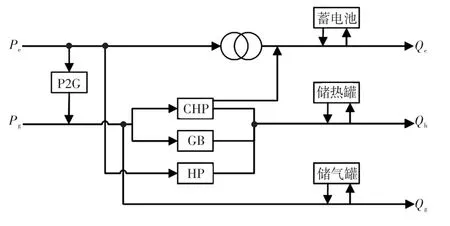
圖1 EH的結構Fig.1 Structure of EH

1.2 能量轉換設備和能量儲存元件

1.2.1 能量轉換設備

1）熱電聯產系統

熱電聯產可利用熱機或發電站同時產生電能和熱能，其電功率可由燃氣輪機GT（gas turbine）輸出，熱功率可由余熱鍋爐WHB（waste heat boiler）輸出。

GT是以流動的氣體帶動葉輪旋轉，將燃料的能量轉化為電能的設備，其模型可表示為電-氣轉換效率的線性函數，即

WHB是對GT發電過程中產生的余熱進行回收，用以生產熱能的設備，其模型可表示為

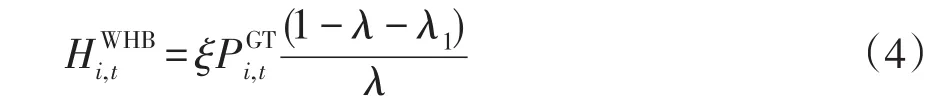
2）P2G、熱泵、燃氣鍋爐

電轉氣 P2G（power to gas）、熱泵 HP（heat pump）及燃氣鍋爐GB（gas boiler）模型與GT模型類似，均為能量轉換效率的線性函數，可參照式（3）。

1.2.2 能量儲存設備

1）儲電裝置

儲電設備是調節系統穩定運行、實現削峰填谷的重要手段，其模型可表示為

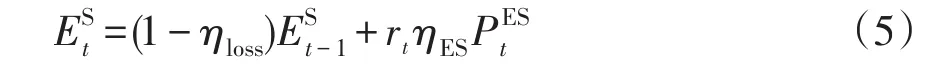
式中：ESt為t時刻儲電裝置存儲的能量；ηloss為儲能自損失率；rt為t時刻儲電裝置的充放電狀態，充電時取1，放電時取-1；ηES為儲電裝置的充放電效率；PESt為t時刻的充放電能量，電量大小要滿足

2）儲氣和儲熱裝置

儲氣和儲熱裝置模型表達式及約束與儲電裝置類似，可參考式（5）和式（6）。

1.3 綜合需求響應

IDR是在DR的基礎上，通過調整峰谷電價，利用IES中不同能源的互補，以其他形式能源替代電能，引導用戶改變用能方式，促進系統穩定運行。

基于電價的IDR是通過引入分時電價機制引導用戶自發調整用電需求，從而減小負載峰谷差值。用戶響應程度與價格變化的關系可由彈性系數表示[11]。彈性系數ε可表示為需求變化率與價格變化率之比，即

式中：Qj和ΔQj分別為電負荷及其改變量；Ci和ΔCi分別為電價及其改變量。

由此可以得到以彈性系數和需求彈性矩陣表示的用戶負荷需求變化模型，即

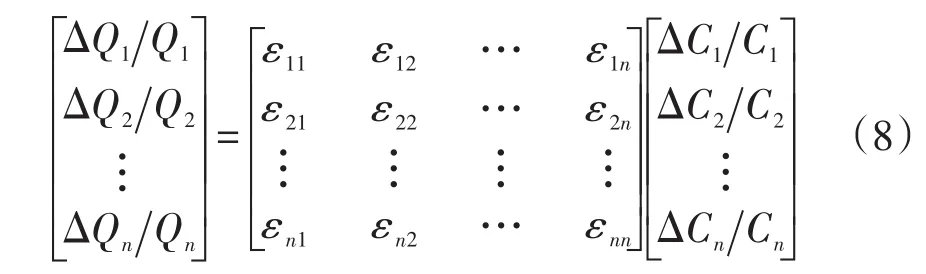
式中，各彈性系數可通過歷史數據分析得到[6]。由式（8）可以得到響應后的電負荷情況，即

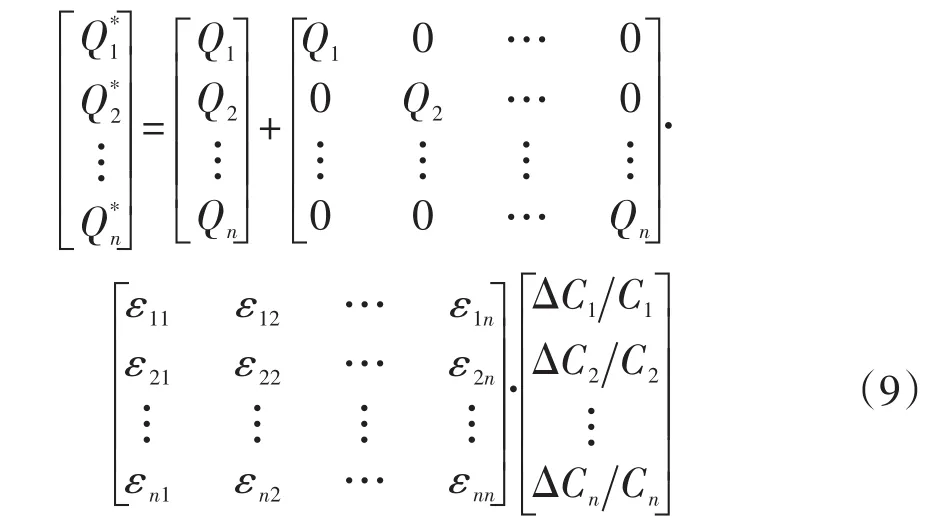
式中，Q*j為用戶對分時電價做出響應后的電負荷需求。

2 計及IDR的電-氣-熱EH調度模型

在滿足系統運行約束的前提下，1個多能耦合系統往往要考慮經濟和環保等多個方面。本文構建了1個以供能公司成本和綜合碳排放量最低為目標的調度模型，并考慮了相關約束。針對風電及負荷預測的不確定性，本文采用模糊參數表示風電及負荷預測值，將確定的系統約束改為模糊機會約束。

2.1 目標函數

模型以供能公司運營成本最低和綜合碳排放量最低為目標函數。運營成本包括購買能源的成本、EH內設備的運維成本和火電機組出力成本。碳排放量主要來源于GT、GB和WHB。本模型中忽略風電出力的成本，運營成本目標函數可表示為

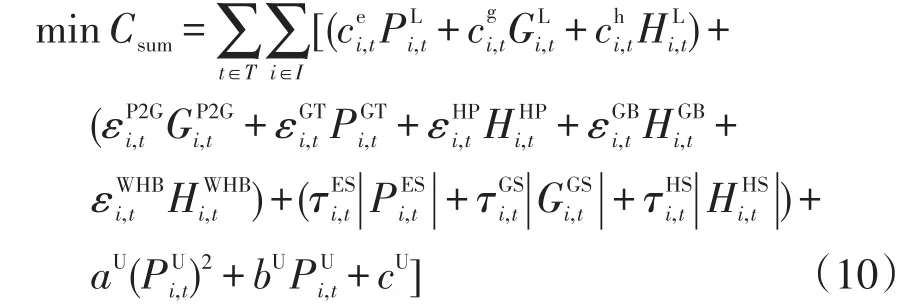
式中：Csum為供能公司運營成本；I為系統節點集合；T為響應時間集合；和分別為購買的電、氣、熱功率；和分別為購買相應單位功率的價格；和分別為P2G、GT、HP、GB和WHB輸出的功率；、分別為相應設備的運維成本系數；和分別為儲電、儲氣和儲熱裝置的輸出功率；和分別為儲能裝置的運維成本系數；為火電機組的輸出功率；aU、bU和cU為火電機組的成本系數。

碳排放量目標函數表達式為

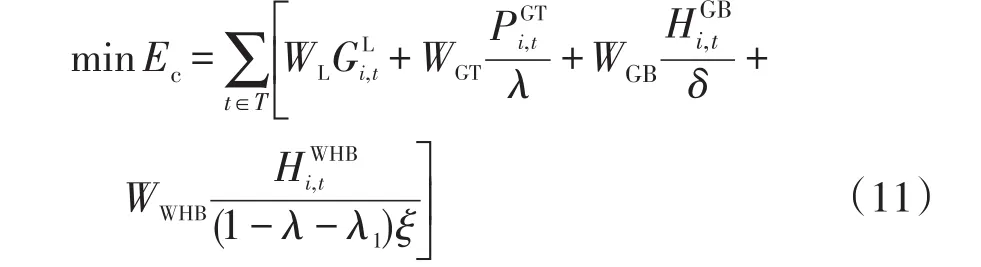
式中：Ec為CO2排放量；WL為上級能源供應商處購買單位氣功率轉化的CO2排放量；WGT、WGB和WWHB分別為GT、GB和WHB單位輸出功率的CO2排放量；δ為燃氣鍋爐的轉換效率。

在保證系統運行約束的前提下，為使系統具有良好的經濟性和環保性，對目標函數式（10）和式（11）做歸一化處理后進行線性加權建模[12]。綜合目標函數可表示為

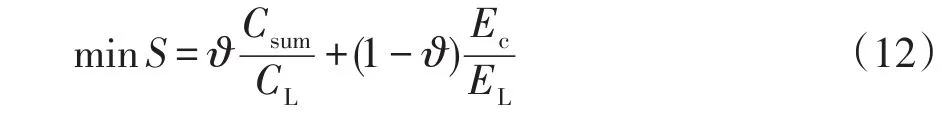
式中：S為綜合得分，其值越小越優；?為成本權重系數，取值范圍[0，1]；CL為只從上級能源供應商處購買能源的成本；EL為只考慮上級能源供應商處轉化CO2排放量。

2.2 約束條件

由于風電及負荷預測的不確定性，本文采用基于可信性測度的模糊機會約束規劃求解，其具體形式如下。

（1）電負荷平衡約束及火電機組出力限制可表示為

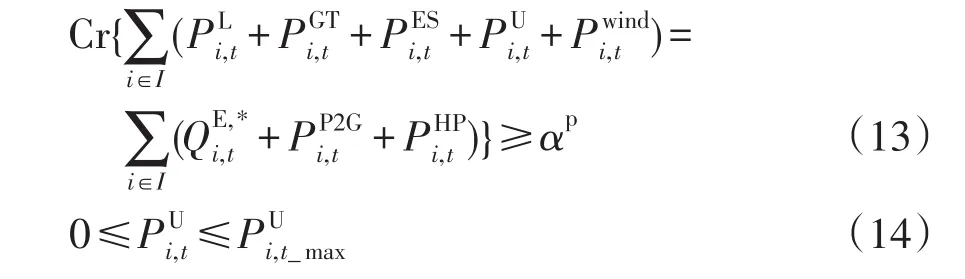
式中：Cr{·}為{·}中事件的可能性；αp為置信水平；為實行IDR后的電力負荷；為火電機組出力上限；為風電出力。

（2）天然氣負荷平衡約束可表示為

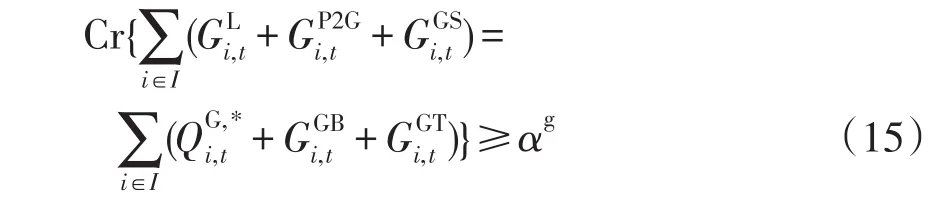
（3）熱負荷平衡約束可表示為

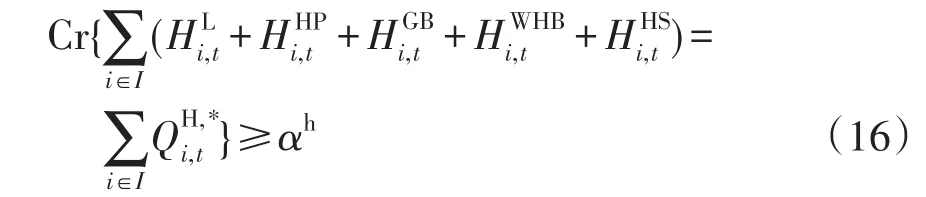
4）能量轉換設備及儲能設備出力限制

各能量轉換及儲能設備出力不應超出其各自出力上限、下限。以GT和電儲能為例，約束條件可分別表示為

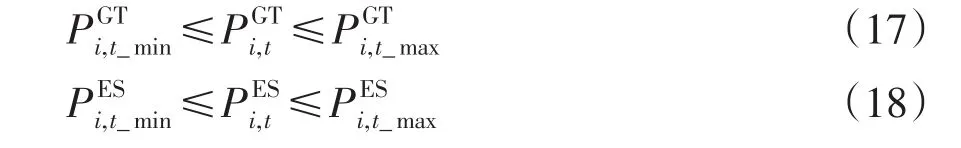
2.3 求解方法

本文對模型采用分群渦流搜索算法[13]進行求解。渦流搜索算法[14]受渦流模式的啟發，是一種采用新的自適應步長調整方案的算法，其算法流程如下。

步驟1產生初始解。設解空間的維數為D維，第j維的取值范圍為[elower,j，eupper,j]，則可確定搜索空間的中心 μ0為

步驟2產生隨機備選解。隨機備選解為通過以 μ0為中心的高斯分布隨機產生的n個數。高斯分布的概率密度函數為

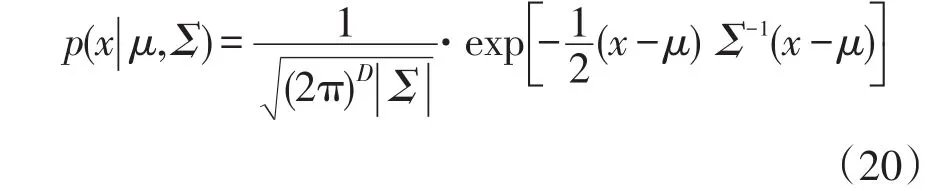
式中：Σ=σ2[I]d×d，其中，[I]d×d為單位矩陣，σ為標準差；x為隨機變量；μ=μ0。σ的初始值σ0可表示為

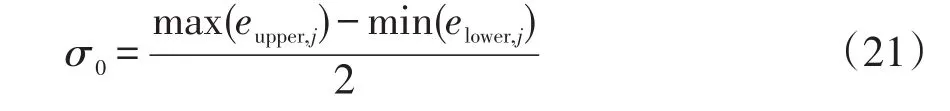
步驟3對當前解進行更新。將上一次迭代生成的隨機備選解帶入目標函數，比較本次迭代最優解和歷次迭代最優解的適應度大小，將適應度較小的備選解更新為新的最優備選解gbest，并將其作為新的搜索空間中心，產生新的備選解。如此循環直到算法結束。

（4）對解空間半徑進行更新。搜索空間的半徑r會隨著迭代的進行自適應減小。初始解的搜索半徑r0為

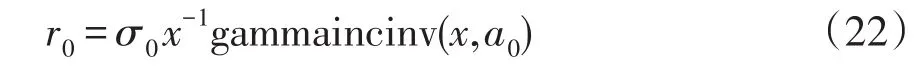
式中：x=0.1；a0=1。

第i次迭代的搜索半徑按下式更新：

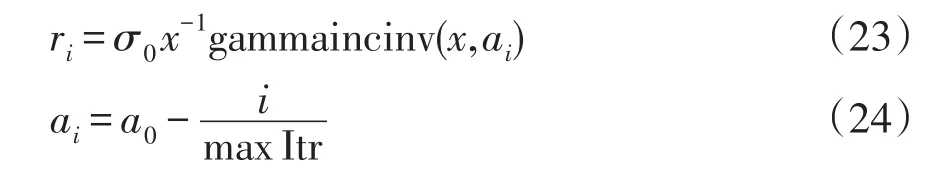
式中，maxItr為最大迭代次數。

渦流搜索算法示意如圖2所示。

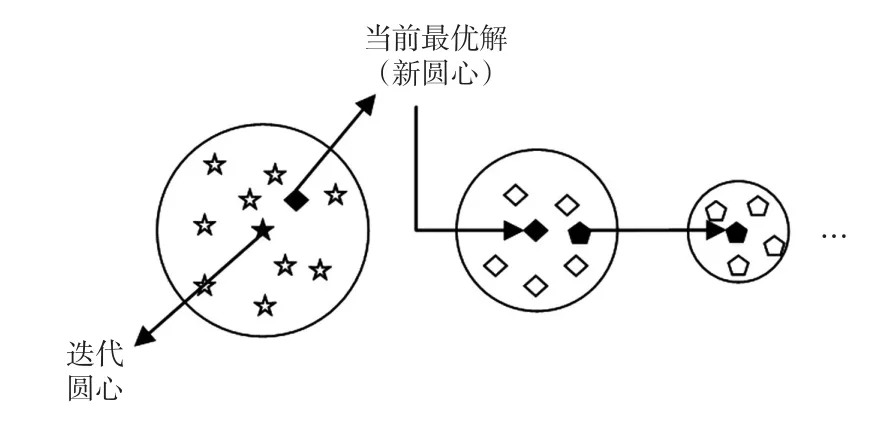
圖2 渦流搜索算法示意Fig.2 Schematic of vortex search algorithm

分群渦流搜索算法是在每次迭代中設置兩個搜索圓心。將備選解分為兩組；種群1以歷次迭代最優解 μbest為圓心產生；種群2以當前迭代最優解關于初始圓心μ0對稱點為圓心產生，即

式中，μ′i為種群2的搜索圓心。為防止迭代前期種群過于分散影響搜索能力，通過下式限制種群2備選解分布：

式中，μ″i為優化后種群2的搜索圓心。

由式（26）可知，μi在迭代前期的位置靠近gbest，在迭代后期的位置更靠近gbest關于 μ0的對稱位置，保證了算法備選解的多樣性。

3 模糊機會約束

3.1 模糊參數隸屬度函數

風電和負荷預測的模糊參數可由梯形函數或三角形函數[15]表示，即

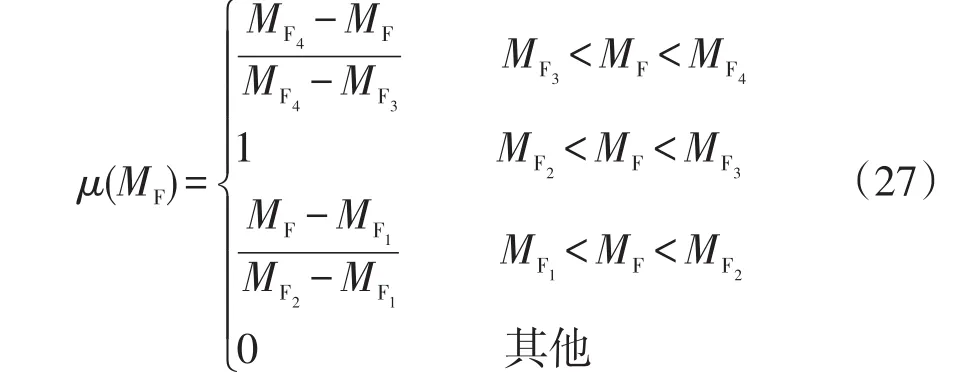
式中：μ(MF)為隸屬度函數；MFi為梯形函數的隸屬度參數，i=1，2，3，4，其計算公式為

式中：ωi為比例系數，其值可根據歷史數據確定；Mfc為參數預測值。當 ω2=ω3=1，即 MF2=MF3=Mfc時，模糊參數為三角形函數。本文采用梯形模糊參數表示模糊變量。

3.2 模糊機會約束的清晰等價類

求解模糊機會約束規劃問題的關鍵是處理機會約束[8]，本文采用將機會約束轉化為清晰等價類的方法，對模型進行求解。文獻[8]中詳細介紹了清晰等價類的原理及轉化方法，故本文直接對式（13）、式（15）和式（16）做清晰等價類處理。

（1）電負荷平衡約束的清晰等價類處理可表示為

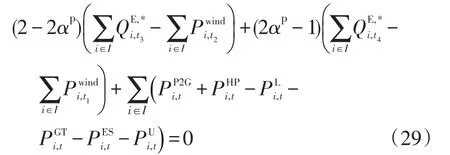
（2）氣負荷平衡約束的清晰等價類處理可表示為

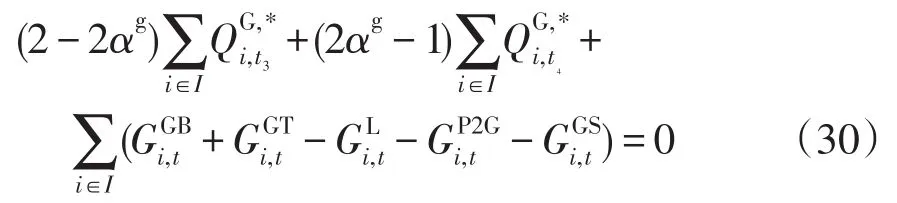
（3）熱負荷平衡約束的清晰等價類處理可表示為

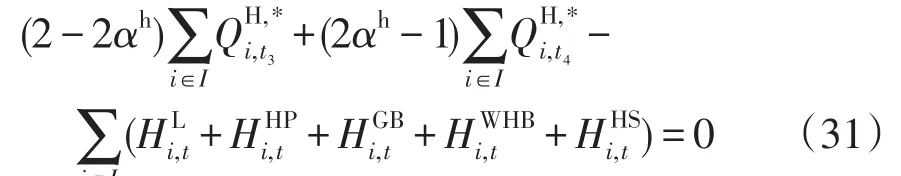
4 算例分析

4.1 算例參數

為驗證所提出的模型和算法的有效性，本文選取冬季典型日某一地區為仿真算例[16]，假設調度運行周期為1 d（24 h），單位調度時間為1 h。設備運行參數如表1所示。

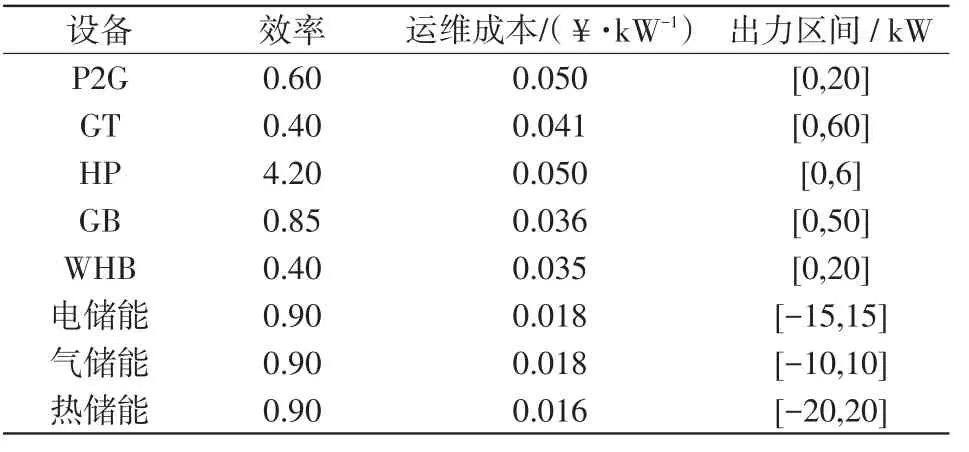
表1 設備運行參數Tab.1 Operating parameters of equipment

從能源供應商處購買能源[17]的價格見表2，其中電價一欄中“/”左右分別為采取IDR前后的價格。

表2 能源購買價格Tab.2 Energy purchase prices

該地區電、氣、熱負荷及風電出力預測如圖3所示。從圖3可以看出，該地區用電時段多集中在日間，夜晚用電較少；氣負荷整體需求較穩定，波動較小；在冬季午間用熱負荷較少，其余時間用熱較多；風電出力多集中在夜間，白天出力較少。

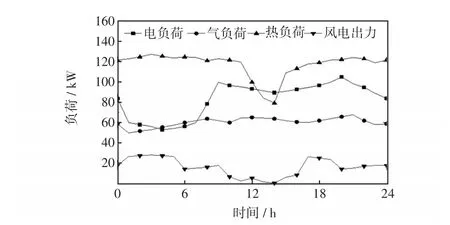
圖3 電、氣、熱負荷及風電出力Fig.3 Power，gas，heat loads and wind power output

梯形隸屬度參數如表3所示，由于風電出力相比負荷更難以預測，故風電的隸屬度參數擴展幅度更大[15]。

表3 隸屬度參數Tab.3 Parameters of membership

4.2 算例結果與分析

為定量分析采取IDR策略后目標函數與可信性置信水平α的關系。結合算例實際情況，取成本權重系數?為0.6，碳排放量權重系數為0.4。

通過分群渦流搜索算法對調度模型進行求解，可信性置信水平α從0.65開始，以0.05步長增加至1.00，所得結果如圖4所示。

由圖4（a）可知，隨著置信水平α的不斷升高，綜合得分S也不斷增大，即高可靠性依賴高投入；由圖4（b）可知，隨著置信水平α的不斷升高，系統運營成本也不斷增大，與圖4（a）曲線均勻上升不同，成本-置信水平曲線在α∈（0.75，0.85]∪（0.90，0.95]內上升緩慢，可認為在該區間內風險降低并沒有帶來成本顯著提高；由圖4（c）可知，碳排放指標隨置信水平α的升高呈波動型，在α∈（0.70，0.80]∪[0.85，0.90]內，隨α升高，碳排放指標略有上升或下降，表明在該區間內，在風險降低的同時，碳排放指標不會上升很多，甚至略有下降。

置信水平反映了決策人員對風險把控的能力。在本文EH調度模型中，風險來自風電出力與各類型負荷預測的不確定性，使得系統功率平衡等式約束難以得到滿足。因此，在實際決策時可引入置信水平，在可以承受的風險下選擇最合適的設備出力方案。

綜合圖4結果可以看出，α在0.75～0.80區間段，綜合得分/成本/碳排放指標-置信水平曲線較平穩；α在0.80～0.85區間，碳排放指標-置信水平曲線漲幅較大，綜合得分/成本-置信水平曲線漲幅平穩，說明當α=0.80時已達到了一個較好的置信水平，若想要進一步提高置信水平會導致碳排放指標的增大；α在0.85～0.90區間，成本-置信水平曲線漲幅較大，碳排放指標-置信水平曲線有明顯降低，說明當α=0.85時，若想要進一步降低風險，雖然碳排放指標會降低，但成本會有明顯升高，考慮到成本因素大多時間比碳排放更重要，故認為α=0.85不是最優置信水平；α在0.90～0.95區間，碳排放指標-置信水平曲線漲幅較大，綜合得分/成本-置信水平曲線漲幅平穩，說明當α=0.90時想要進一步降低風險，會引起碳排放指標的大幅增長。綜上所述，α=0.80為本算例的最優置信水平。

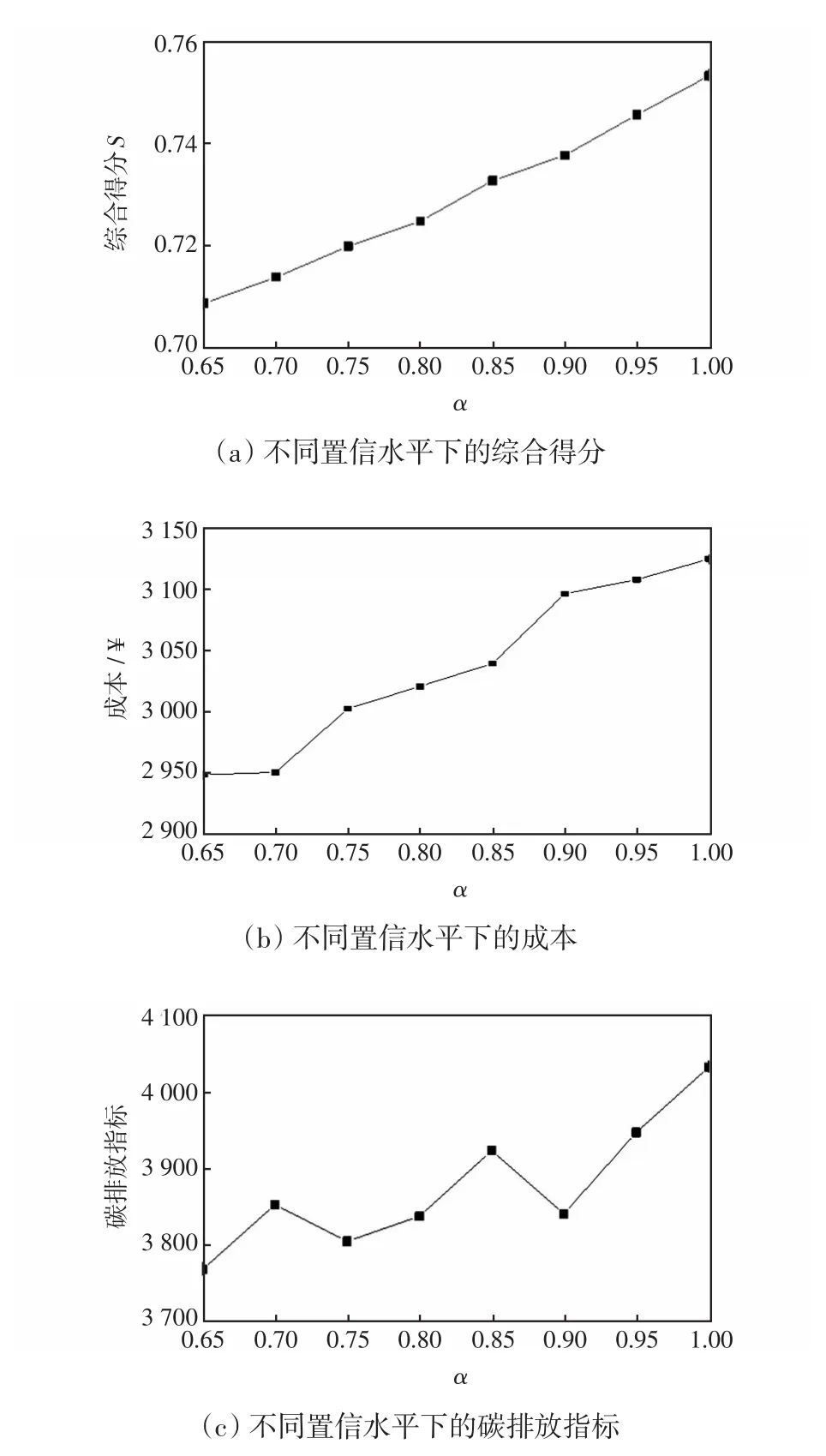
圖4 不同置信水平下的目標Fig.4 Objectives at different confidence levels

取α=0.80，對不采取IDR模型進行求解，將采取IDR模型通過分群渦流搜索算法求解，結果對比如表4所示。采取IDR后，由于用電峰時刻電價升高，平、谷時刻電價降低，用戶會選擇將部分負荷由峰時刻向平、谷時刻轉移，并選擇其他能源替代電能，使負荷特性曲線更加平滑。

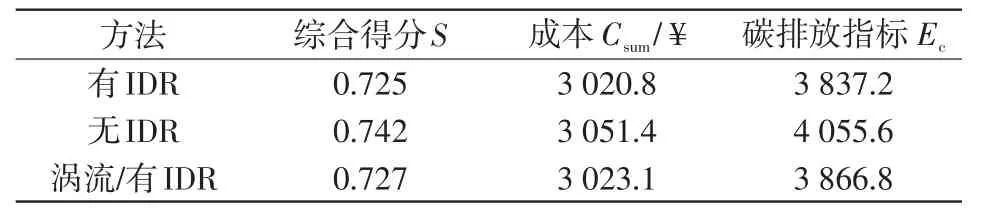
表4 α=0.80時采取IDR與否的結果對比Tab.4 Comparison of results with and without IDR when α=0.80

從表4可以看出，實施IDR后，模型的綜合得分、成本和碳排放指標均有明顯降低，說明IDR可以有效引導用戶調整負荷，合理分配各機組出力，既可以減小系統運行壓力，提高系統可靠性，又可以降低能源成本，提高系統運行經濟性。采用分群渦流搜索算法求解模型，其綜合得分、成本和碳排放指標都稍低于渦流搜索算法的結果，證明該算法有較好的準確性。

5 結論

本文在能源耦合日益密切的背景下，針對風電出力和負荷預測的不確定性，計及含模糊參數的模糊機會約束，建立了電-氣-熱EH多目標優化調度模型，并結合相關算例進行分析，得到以下結論。

（1）成本-碳排放指標綜合評價與置信水平相關，置信水平越高，模型綜合得分越高，即高可靠性會引起高成本和高碳排放指標，高風險帶來高回報。

（2）在根據實際需求確定各目標權重比例后，可通過仿真分析得到該模型權重下的最優置信水平。在可接受的風險水平下，通過將模糊機會約束轉化為清晰等價類可避免模糊模擬過程，實現快速求解。

（3）IDR可有效改善系統負荷曲線，減小系統運行壓力，降低能源成本，提高系統運行的可靠性和經濟性。