一道常見不等式題的“變臉記”

龔才權

(江蘇省靖江高級中學 214500)

不等式求最值題是高中數學的一個難點，本文嘗試從一道常見的不等式求最值題入手，實施一系列的“變臉術”，從而生成一系列的不等式求最值題，以此歸納小結不等式求最值題的解法.

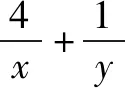
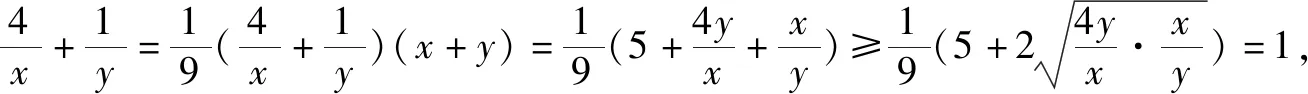
對“題根”實施“變臉術”，令x=m+2，y=2n+1，得到題1.

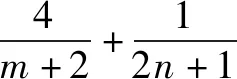
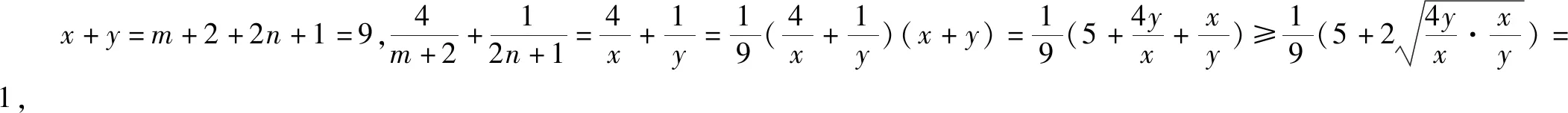
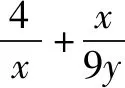
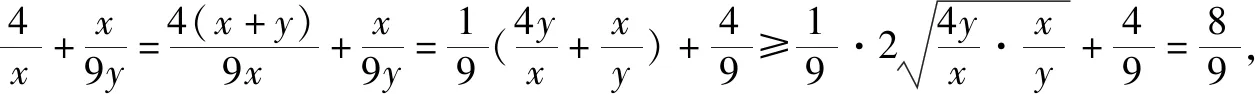
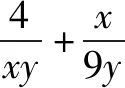
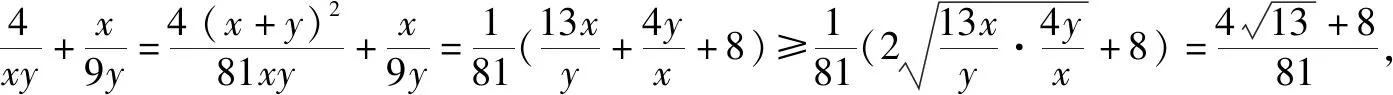
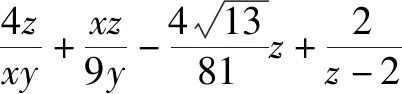
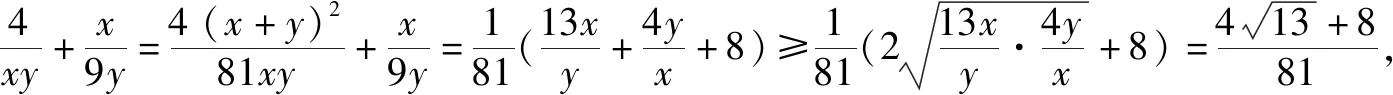
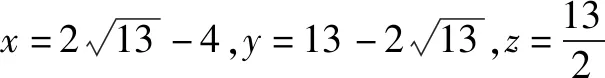
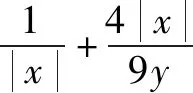
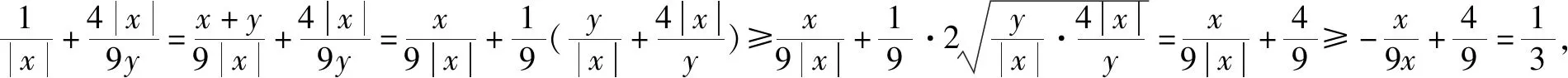
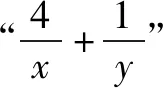
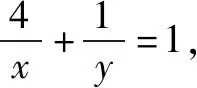
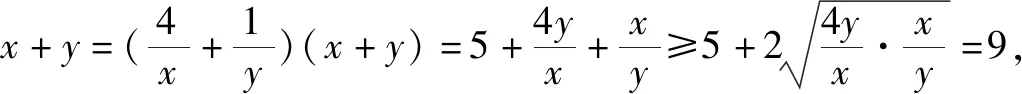
題7 若x>0，y>0，且x+4y-xy=0，求x+y的最小值.

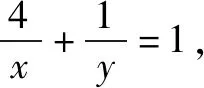
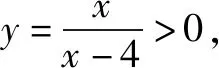
對題7實施“變臉術”，將“x+4y-xy=0”改寫為“x+4y-xy+5=0”，得到題8.

題8 若x>0，y>0，且x+4y-xy+5=0，求x+y的最小值.

解令t=x+y，得x=t-y，代入x+4y-xy+5=0中，得y2+(3-t)y+t+5=0，由判別式Δ=(3-t)2-4(t+5)=t2-10t-11≥0，解得t≥11或t≤-1，因為x>0，y>0，所以t≥11，即x+y的最小值為11，此時x=7，y=4.

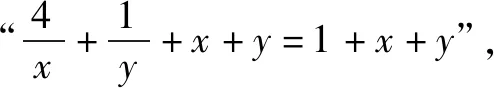
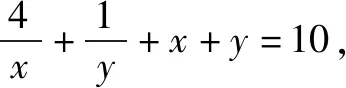
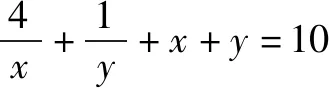
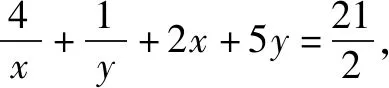
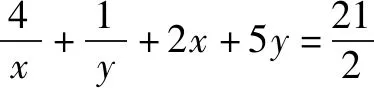
學生總有解不完的題！總有做不完的試卷！新一輪數學課改的目標就是要把學生從題海戰術中解放出來.怎樣解放？就是以數學高考為指揮棒，讓數學高考能真正考查出學生的數學思維能力.數學高考試題以能力立意，學生只有數學思維能力強，才能考得好！不是多刷刷題就能考得好！所以，現在題海戰術要不得.題海無涯，回頭是岸！岸在哪里？岸在數學教材中！岸在平時數學學習一點一滴的思考中！數學教材中的每個概念，每個定理，甚至是每道例題，每道習題都能成為我們思考的源頭.我們要不斷地去探究挖掘，才能真正地提高我們的數學思維能力.問渠哪得清如許？為有源頭活水來.從源頭出發，不斷地延伸，不斷地拓寬，變成小溪，變成河流，最后必將匯聚成我們數學的汪洋大海！