滾輪滾針軸承螺栓強度優化設計方法

張 劍， 李鑫斌， 姜艷紅*， 丁士釗， 劉 靜

(1.中浙高鐵軸承有限公司， 龍游 324400； 2. 重慶大學機械與運載工程學院， 重慶 400044； 3.西北工業大學航海學院， 西安 710072； 4.西北工業大學無人水下運載技術工業和信息化部重點實驗室， 西安 710072)

滾輪滾針軸承通常在民機襟翼和縫翼等部件中作為滾輪使用[1]。與一般滾針軸承相比，滾輪滾針軸承內圈主要采用螺栓與滑輪架連接，其內圈和螺栓為一體化結構，外圈可在滑軌上滾動，為滑輪架在滑軌上滑動提供滾動支撐[2]。滾輪滾針軸承螺栓內部注油孔與螺栓外面圓角的結構和尺寸將改變滾輪滾針軸承螺栓的應力和變形，影響滾輪滾針軸承的使用壽命。因此，開展滾輪滾針軸承注油孔與螺栓外面圓角結構和設計參數優化方法研究，減小軸承螺栓的應力和變形，提高滾輪滾針軸承的使用壽命。

在滾動軸承優化設計方面，已經有眾多學者開展了相關研究。孫玉飛等[3]以軸承額定動載荷為優化設計目標，對深溝球軸承節圓直徑、鋼球直徑和數量進行了優化設計。張亞軍等[4]以油膜厚度、接觸應力和變形量為優化目標，建立了軸向載荷下的圓柱滾子軸承多目標優化模型，確定了滾子端面和擋邊最佳的位置參數。Waghole等[5]采用人工蜂群算法、差分搜索算法、網絡搜索法以及混合方法，以滾針軸承動態承載能力最大為優化目標，對滾針軸承滾子直徑、滾子長度和滾子數等參數進行優化設計。Zhao等[6]建立了鋼絲球軸承優化設計數學模型，以摩擦力矩最小為優化目標，對球數、球的直徑、節圓以及接觸角進行了優化設計。Charitopoulos等[7]以減小摩擦力矩為優化目標，考慮軸承區域的散熱、共軛散熱以及潤滑油區域的剪切減薄和氣穴現象，提出了一種基于計算流體動力學(computational fluid dynamics，CFD)的熱流體力學計算方法，對推力軸承兜孔進行了優化設計。莫易敏等[8]采用遺傳算法，以降低圓錐滾子軸承摩擦力矩為優化目標，對圓錐滾子軸承的節圓直徑、滾子直徑、滾子有效長度、外圈接觸角、滾子半錐角以及滾子端面與內圈擋邊面的接觸高度進行優化設計。閆軒等[9]構建了溫度影響的球軸承動力學模型，采用主成分分析法對預緊力與軸承動態指標間的耦合關系實施動態降維優化。張強強等[10]建立了一種適用于高轉速脂潤滑條件的生熱模型及傳熱模型，以降低軸承外圈溫度為優化目標，對軸承轉速進行優化。趙方偉等[11]以降低軸向軸承溫升為優化目標，采用試驗方法對軸承載荷和轉速進行優化。張功學等[12]建立了軸承總成內腔的數值分析模型，分析了軸承運動對流暢內部氣相流動的影響，揭示了轉速對軸承總成腔內的傳熱特性的影響，從而對軸承轉速進行優化。綜上所述，目前的研究主要集中在球軸承、圓柱滾子軸和圓錐滾子的結構進行優化設計。雖然少量研究對滾子軸承的結構進行了優化，但是在滾輪滾針軸承螺栓結構參數的優化設計方面研究較少。

針對這一問題，以螺栓最大應力和變形為優化目標，提出了滾輪滾針軸承螺栓強度優化設計方法。首先，基于三維建模軟件，建立了滾輪滾針軸承參數化模型；然后，運用有限元方法，提出了滾輪滾針軸承整體有限元仿真模型，分析了注油孔設計參數和螺栓上圓角設計參數對螺栓強度的影響規律；最后，采用響應面分析方法，建立了以螺栓最大應力和最大變形最小為優化目標的滾輪滾針軸承多目標優化模型，獲得了螺栓注油孔孔徑和螺栓上圓角的最優化設計參數。

1 優化設計方法描述

因響應面優化(response surface optimization)方法具有計算快且精度高等優點，在各種機械零件的結構優化優化設計中獲得了廣泛的應用[13-18]。因此，論文采用響應面法對滾輪滾針軸承螺栓結構進行優化設計。該優化算法的流程，如圖1所示。算法的具體步驟包括：①在三維建模軟件Solidworks中對滾輪滾針軸承進行參數化建模；②在有限元分析軟件ANSYS Workbench中建立滾輪滾針軸承整體有限元模型，并對其進行靜力學分析；③在AYSYS Response Surface Optimization模塊中構建優化系統，對滾輪滾針軸承螺栓注油孔和圓角設計參數進行優化設計；④對選用的優化參數進行驗證，確定其合理性。

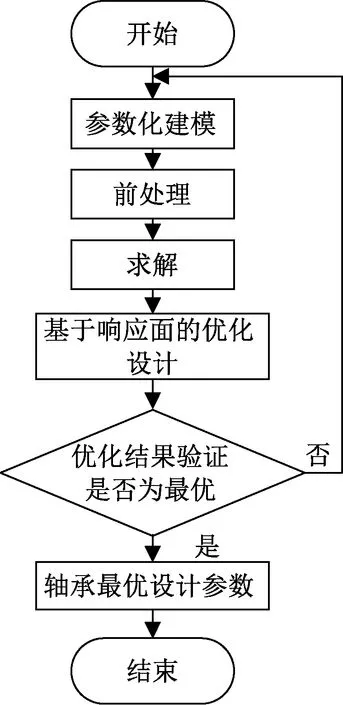
圖1 優化設計方法流程圖Fig.1 Flow chart for the proposed optimization method

2 參數化建模

滾輪滾針軸承的注油孔分為三段。各段注油孔優化參數代號，如圖2所示。對這三段注油孔設計參數進行多參數優化，各選取參數的優化設計范圍，如表1所示。

3 有限元分析

3.1 有限元模型

滾輪滾針軸承的外圈和滾針材料為G20Gr2Ni4，螺栓、機架以及隔離套材料為GGr15Z。兩種材料的力學性能，如表2所示[19]。滾輪滾針軸承的網格劃分主要采用四面體主導的網格劃分方法(Tetrahedrons)，將單元尺寸設置為2 mm，網格質量定義為High，圓角處的網格尺寸設為0.25 mm，進行細化。軸承整體有限元模型，如圖3所示。該模型有102 255個單元和168 524個節點。

3.2 接觸及邊界條件

滾輪滾針軸承運行過程中，滾針和滾針、滾針和外圈以及滾針和內圈之間一般為滾動摩擦，故設置滾針和滾針、滾針和外圈以及滾針和內圈之間的接觸類型為Frictional，摩擦系數設為0.05。外圈和螺栓、機架和螺栓以及機架和隔離套之間為滑動摩擦，故設置外圈和螺栓、機架和螺栓以及機架和隔離套之間的接觸為Frictional，摩擦系數設為0.2。根據滾輪滾針軸承的運行條件，軸承是靠螺栓連接固定在機架上的，因此在螺栓有螺紋一端和機架上添加固定約束(圖4中的A位置)，在軸承外圈上添加z軸負方向的-11 000 N的力，(圖4中B位置)。

圖4 滾輪滾針軸承邊界條件Fig.4 The boundary condition of the tack roller needle roller bearing

3.3 仿真結果分析

通過對該滾輪滾針軸承進行靜力學分析計算，得到螺栓滾輪滾針軸承的整體應力云圖、螺栓應力云圖和變形云圖，如圖5～圖7所示。

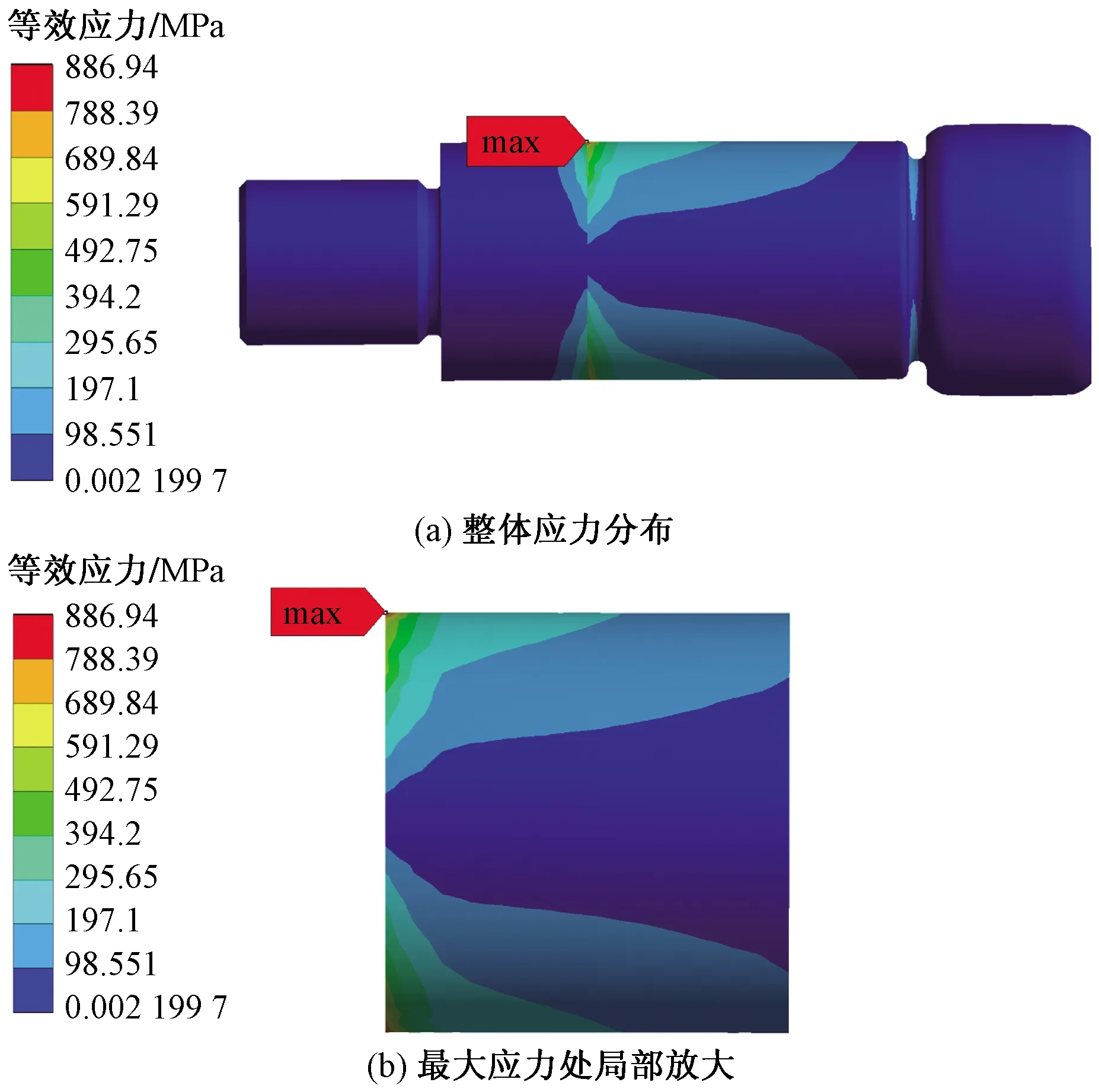
圖5 滾輪滾針軸承應力云圖Fig.5 The stress distribution of the tack roller needle roller bearing

圖6 螺栓應力云圖Fig.6 The stress distribution of the bolt

圖7 螺栓變形云圖Fig.7 The deformation distribution of the bolt

圖5～圖7顯示，滾輪滾針軸承的最大應力為886.94 MPa，位于隔離套與機架的接觸處，該值小于GGr15Z的屈服強度1 815 Pa。螺栓最大應力為247.68 MPa，位于滾針一端與滾道的接觸處，該值小于GGr15Z的屈服強度1 815 Pa；其最大變形為0.132 92 mm，位于外力施加處。結果表明，該滾輪滾針軸承的強度滿足設計要求。

4 基于響應面法的滾輪滾針軸承結構優化設計

4.1 響應面法優化原理

響應面是一個輸出參數用輸入參數表示的變性質函數，可通過若干個實驗確定輸出參數與輸入參數的近似關系，從而快速得到所有設計實驗的輸出參數近似值，不需要執行所有的設計實驗。響應面的精度取決于解變化的復雜性、原始設計實驗的點數和響應面類型等因素。

響應面的主要類型有：基因聚類算法、標準響應面-全2階多項式、克里格法、非參數回歸法、神經網絡以及稀疏網格法。論文采用基因聚類算法[20-21]，該方法是一種基于遺傳算法生成不同類型的響應面同時求解的方法。響應面的適應度函數用于確定最優的響應面，它既考慮了設計點上響應面的精度，又考慮了響應面的穩定性(交叉驗證)。遺傳聚合響應面可以是單個響應面，也可以是多個不同響應面的組合(通過遺傳算法中的交叉操作獲得)。

利用不同模型的加權平均，可將基因聚類算法響應面表示為

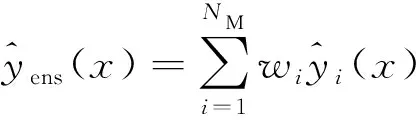
(1)

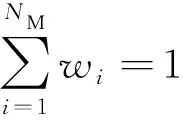
(2)

式(2)中：wi≥0，1≤i≤NM。

為了獲得最佳權重因子值，需將設計點的均方根誤差(root mean squared error，RMSE)最小化，并對相同設計點的均方根誤差進行交叉驗證(PRESSRMSE)。RMSE和PRESSRMSE的表達式分別為

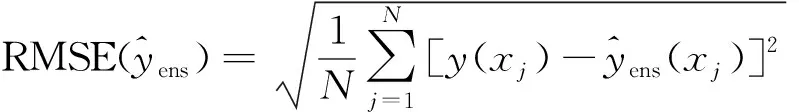
(3)

(4)

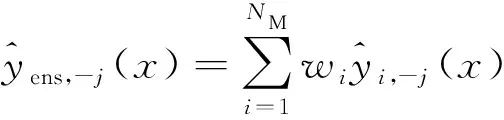
(5)

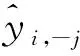
4.2 軸承結構設計參數的靈敏度分析

在所建立的響應面為為中，軸承結構設計參數的敏感性分析結果，如圖8所示。其中，橫坐標為軸承的結構設計參數，縱坐標為靈敏度，靈敏度值越大，說明該設計參數對其影響越大。如圖8(a)所示，單獨考慮各參數時，D6、D8和D9對螺栓最大應力的影響均為正效應，選取參數的靈敏度為：D9>D6>D8；D8對螺栓最大變形的影響為負效應，D6和D9對螺栓最大變形的影響為正效應，其中在建立的響應面中，D6和D8對螺栓最大變形的影響很小，選取參數的靈敏度為：D9>D8>D6。

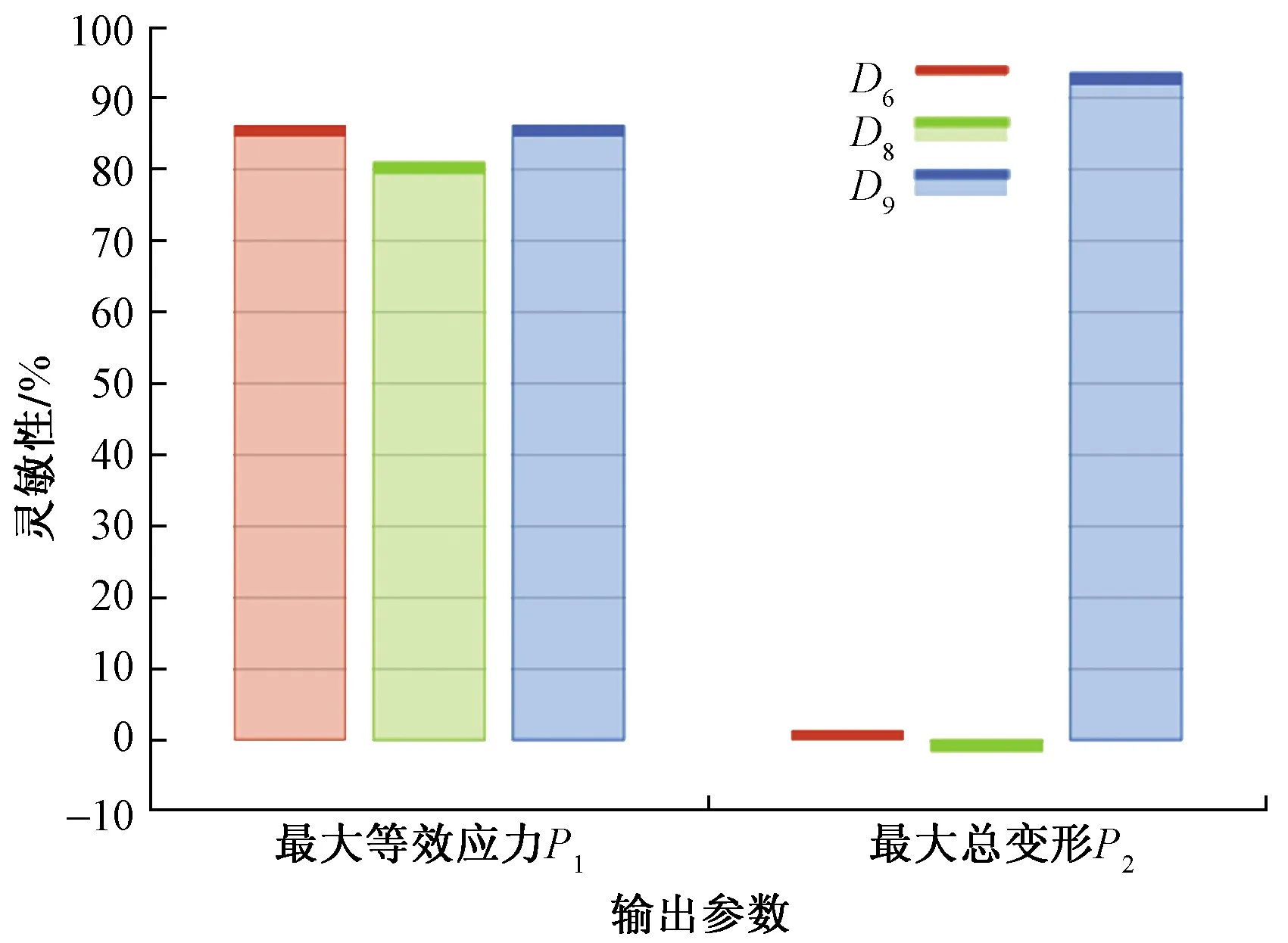
圖8 優化參數靈敏性分析Fig.8 The sensitivity analysis of the optimized parameters

5.3 響應面中各參數螺栓最大應力及最大變形的影響規律

在建立的響應面中，軸承各優化參數對螺栓最大應力以及最大變形的影響規律，如圖9、圖10所示。圖9(a)中，油孔孔徑D9小于2.2 mm時，螺栓最大應力隨著注油孔孔徑D9的增加而增加，D9大于2.2 mm時，螺栓最大應力隨著注油孔孔徑的增加而減小。圖9(b)中，油孔孔徑D8小于1.25 mm時，螺栓最大應力隨著注油孔孔徑D8的增加而增加，D8大于1.25 mm時，螺栓最大應力隨著注油孔孔徑的增加而減小。圖9(c)中，在注油孔半徑D6小于1.56 mm時，螺栓最大應力隨著D6的增加而增加，當D6大于1.56 mm小于1.63 mm時，螺栓最大應力隨著D6的增加而減小當D6大于1.63 mm時，螺栓最大應力隨著D6的增加而增加。

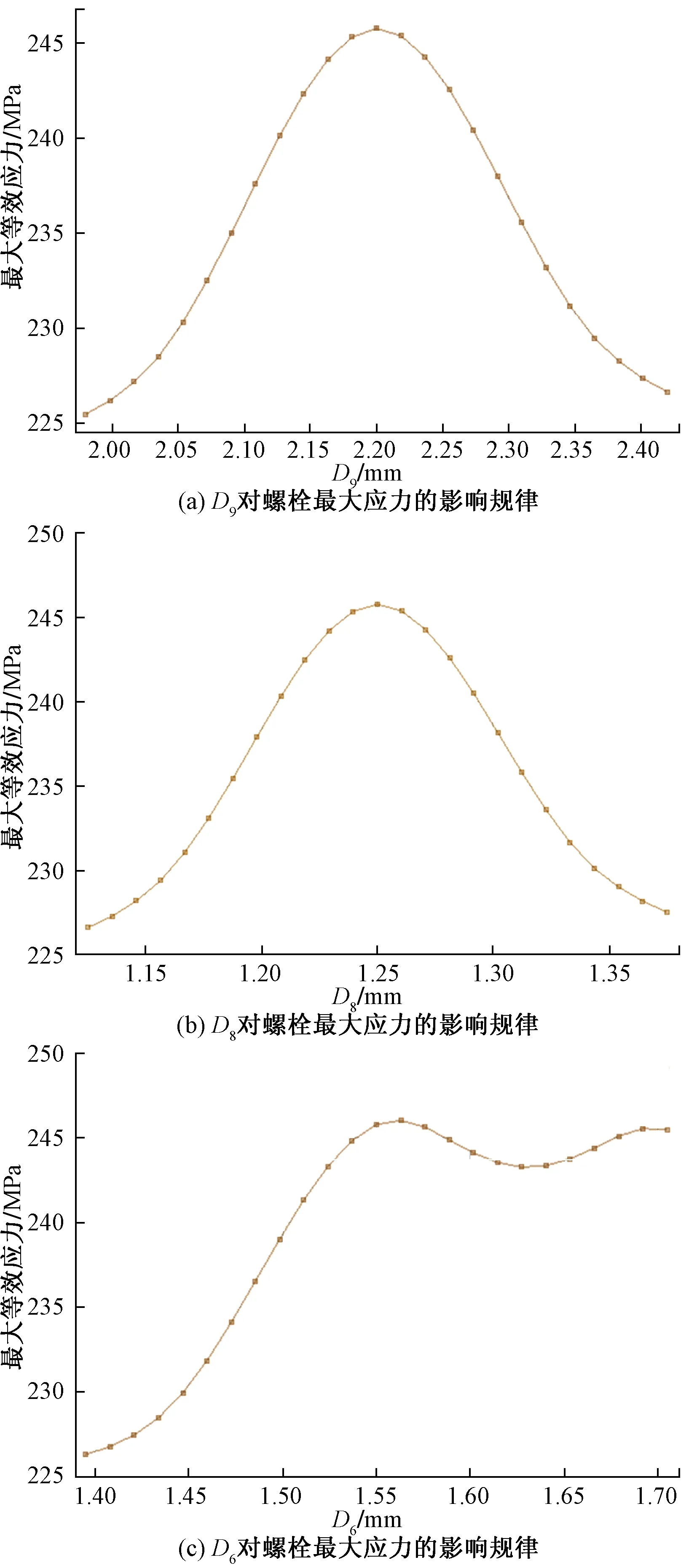
圖9 優化參數對螺栓最大應力的影響規律Fig.9 The effect of optimized parameters on the bolt maximum bending stress

圖10(a)中，螺栓最大變形隨著注油孔孔徑D9的增加而增加。圖10(b)中，D8小于1.19 mm時，螺栓最大變形隨著注油孔孔徑D8的增加而增加，D8大于1.19 mm時，螺栓最大變形隨著D8的增加而減小。圖10(c)中，注油孔半徑D6小于1.66 mm時，螺栓最大變形隨著D6的增加而增加，注油孔半徑D6大于1.66 mm時，螺栓最大變形隨著D6的增加而減小。

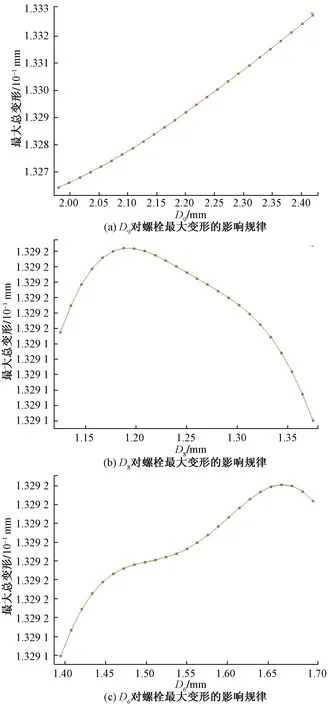
圖10 優化參數對螺栓最大變形的影響規律Fig.10 The effect of optimized parameters on the bolt maximum bending deformation

圖11為建立的響應面的擬合度分析，可以看出，最大等效應力和最大總變形絕大部分都分布在所建立的響應面附近，僅有兩個最大等效應力偏離較大，說明所建立的響應面質量滿足要求。

4.4 優化結果分析

本次優化的目標是：螺栓最大應力最小以及螺栓最大變形最小，優化后Workbench給出的三組注油孔孔徑推薦孔徑如表3所示。根據工程實際，Workbench推薦的參數可能無法加工，因此，對推薦參數進行了修正，以達到加工要求，注油孔孔徑修正參數如表4所示。

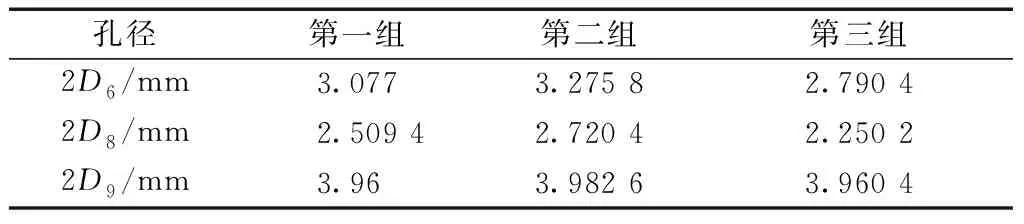
表3 注油孔孔徑優化后推薦數值

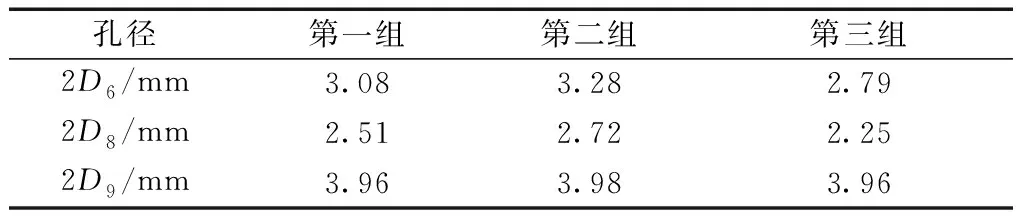
表4 注油孔孔徑修正數值

4.5 優化結果驗證

根據表4中注油孔孔徑修正參數對滾輪滾針軸承的注油孔和螺栓圓角結構設計參數進行修正，分別進行靜力學分析。三組修正孔徑參數的螺栓應力云圖和變形云圖，如圖12～圖14所示。第一組修正參數的螺栓最大應力由247.68 MPa下降至229.21 MPa，下降幅度為7.46%，螺栓最大變形由0.132 92 mm下降至0.132 61 mm，下降幅度為0.23%；第二組修正參數的螺栓最大應力由247.68 MPa下降至228.15 MPa，下降幅度為7.89%，螺栓最大變形由0.132 92 mm下降至0.132 61 mm，下降幅度為0.23%；第三組修正參數的螺栓最大應力由247.68 MPa下降至228.2 MPa，下降幅度為7.86%，螺栓最大變形由0.132 92 mm下降至0.132 64 mm，下降幅度為0.21%。各組修正參數與未優化的螺栓最大應力和最大變形對比結果，如表5所示。綜合三組分析結果，建議選用第二組修正參數作為螺栓滾輪滾針軸承的注油孔孔徑參數。

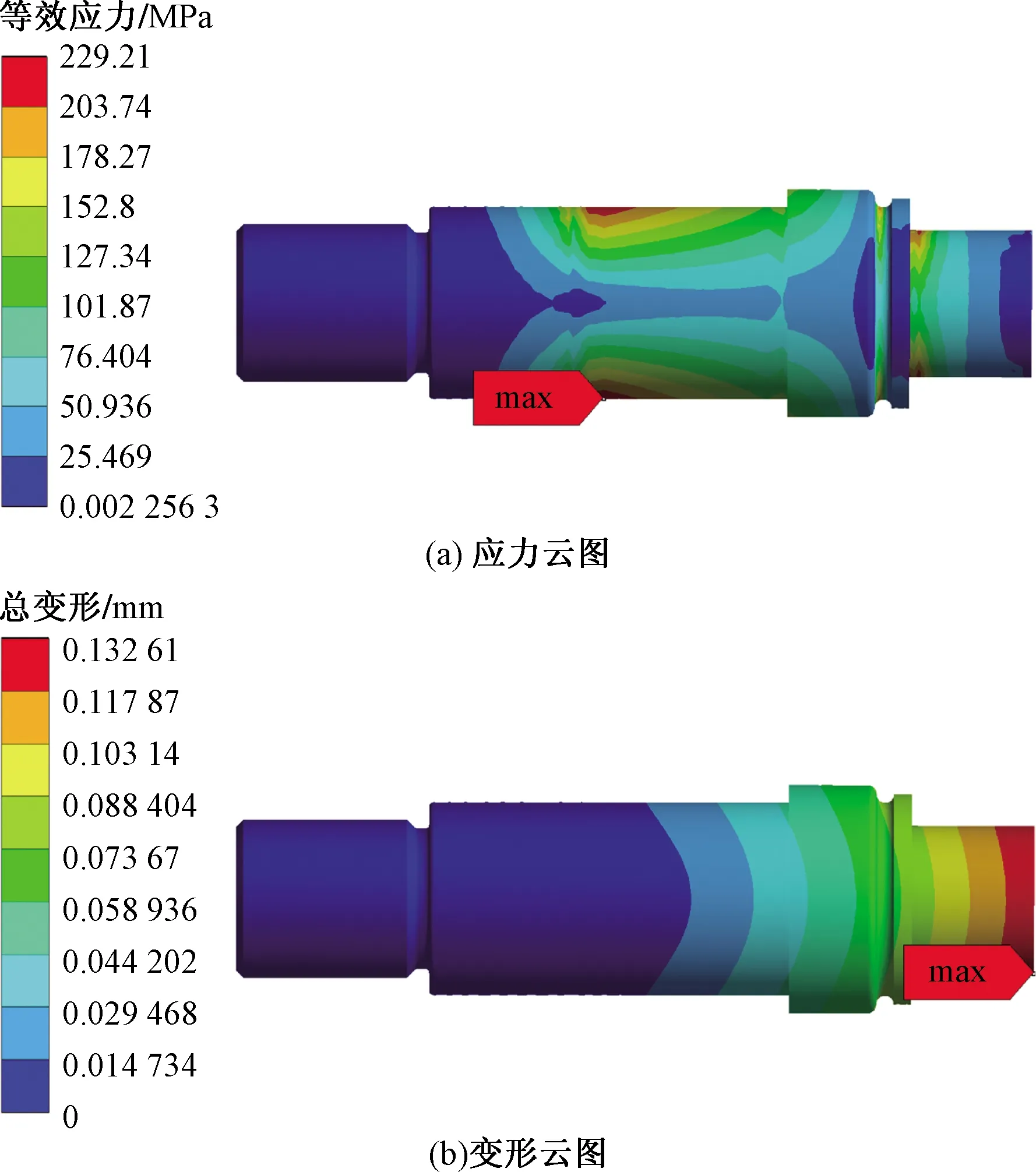
圖12 第一組修正參數螺栓應力云圖、變形云圖Fig.12 The first group of correction parameters bolt stress nephogram, deformation nephogram

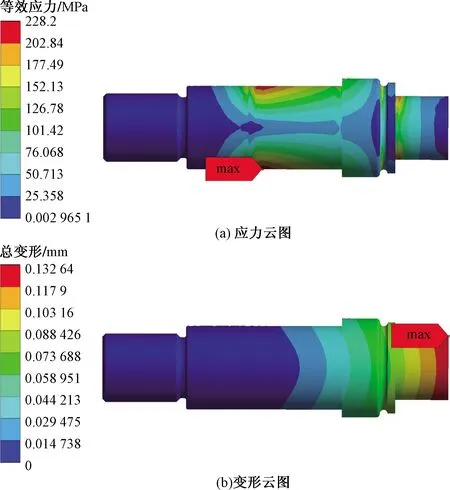
圖13 第二組修正參數螺栓應力云圖、變形云圖Fig.13 The second group of correction parameters bolt stress nephogram, deformation nephogram

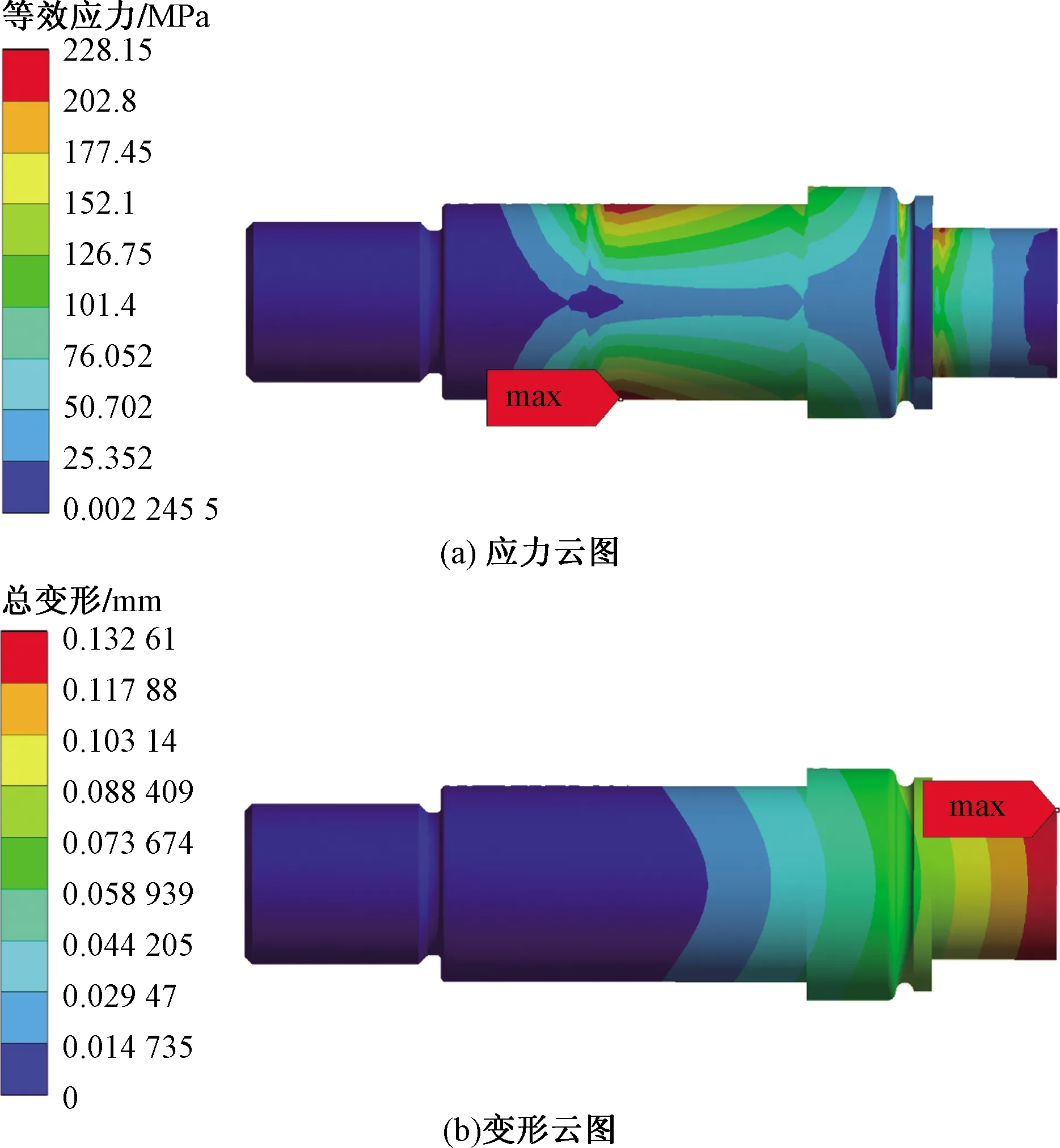
圖14 第三組修正參數螺栓應力云圖、變形云圖Fig.14 The third group of correction parameters bolt stress nephogram, deformation nephogram

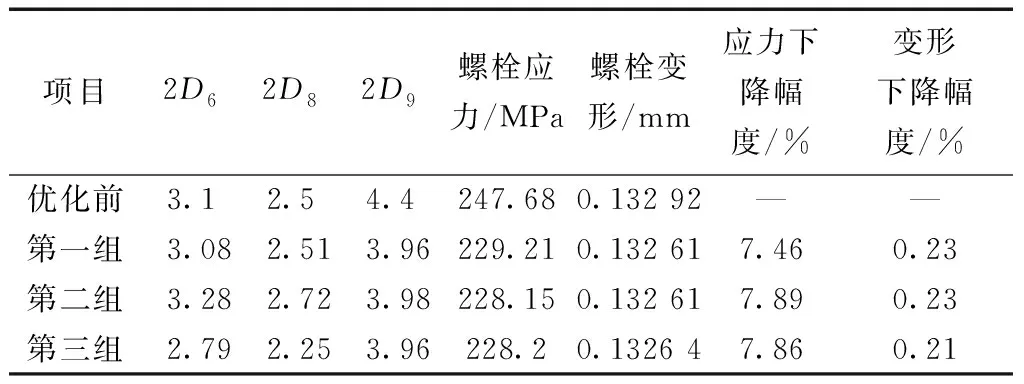
表5 各組修正參數與未優化的螺栓最大應力和 最大變形對比

此外，可以看出，修正參數的螺栓最大應力位置發生了改變，未優化前的螺栓最大應力出現在滾針一端和螺栓的接觸處，而三組推薦參數的螺栓最大應力出現在螺栓和機架的接觸處附近。這可能是因為優化后的螺栓變形減小，導致滾針偏斜量減小，從而導致滾針和螺栓之間的擠壓減小，造成螺栓最大應力位置的改變。

6 結論

以螺栓最大應力和變形為優化目標，提出了滾輪滾針軸承螺栓強度優化設計方法，對滾輪滾針軸承注油孔設計參數進行了優化設計，得出如下主要結論。

(1)滾輪滾針軸承的最大應力出現在隔離套與機架的接觸處，滾輪滾針軸承螺栓最大應力為出現在滾針一端與滾道的接觸處，最大變形出現在外力作用處。

(2)在所建立的響應面中，D6、D8和D9對螺栓最大應力的影響均為正效應，選取參數的靈敏度為：D9>D6>D8；D8對螺栓最大變形的影響為負效應，D6和D9對螺栓最大變形的影響為正效應，D6和D8對螺栓最大變形的影響很小，選取參數的靈敏度為：D9>D8>D6。

(3)在建立的響應面中，D8和D9對滾輪滾針軸承螺栓最大應力的影響規律均為：螺栓最大應力先隨其增加而增加，之后隨其增加而減小。D6對滾輪滾針軸承螺栓最大應力的影響規律為：螺栓最大應力先隨D6的增加而增加，當D6達到1.56 mm后，隨D6的增加而減小，當D6達到1.63 mm后，隨D6的增加而增加。D6和D8對滾輪滾針軸承螺栓最大變形的影響規律為：螺栓最大變形先隨其增加而增加，之后隨其增加而減小。D9對滾輪滾針軸承螺栓最大變形的影響規律為：螺栓最大變形隨其增加而增加。

(4)結合工程實際，推薦了三組注油孔孔徑設計參數。當螺栓滾輪滾針軸承采用這三組修正孔徑參數時，螺栓最大應力相比于優化前下降8%左右，最大變形相比于優化前有所下降。綜合三組參數的驗證結果，建議選用第二組修正參數作為螺栓滾輪滾針軸承的注油孔孔徑設計參數。