時滯獨立狀態下離散控制系統的穩定性分析

孫 鳳 琪

(吉林師范大學數學學院，吉林 四平 136000)

離散系統是實際問題中普遍存在的一類控制系統.為確保在控制上達到較高的精度，需將時滯、不確定性因素對離散系統的影響考慮進去，很多學者在離散時滯不確定系統的穩定性分析方面做了一些研究[1-3].尤其對于時滯依賴情形，參數的增加能夠有效降低系統的保守性，但提高了矩陣不等式條件的復雜性和求解難度.由于時滯獨立情形的穩定性判據簡潔易于操作，有時控制效果往往還會優于時滯依賴情形[4].用結果的保守性來換取控制效果的簡潔性和可行性，控制效果各有所能.在離散時滯依賴方面諸多研究已見諸文獻[5-10]，而對于含有奇異攝動不確定時滯離散這類綜合控制控制系統，時滯獨立的穩定性分析上成果不多，尚需補充完善.

因此，本文對該系統通過設計新的Lyapunov函數，利用相關引理、線性矩陣不等式方法以及新的差分不等式等交叉項界定技術，進行時滯獨立的穩定性研究，對所得結論進行推廣.最后利用數值算例來驗證結論可行性、方法有效性以及相比于文獻的控制效果的優越性.

考慮如下時滯奇異攝動不確定性離散控制系統：

(1)

其中F(k)∈Ri×j是范數有界的不確定系統模型參數矩陣，滿足

FT(k)F(k)≤I.

(2)

其他系統矩陣和相關條件均與文獻[8]的系統(4.1)相同.

1 主要結論

(3)

(4)

證明設計新的Lyapunov泛函如下：

其中Q為對稱正定矩陣，即QT=Q>0，則V(k)為正定的.將V(k)沿著系統(1)向前差分，并由文獻[9]引理3，存在適當維數的矩陣P，對稱陣N和R，使得

-(-xT(k))[(A+ΔA)TZT(ε)Z(ε)(B+ΔB)]x(k-d(k))≤

則ΔV(k)≤ηT(k)G(ε)η(k).其中：

(5)

為求出定理1中未知的參數變量，需要將不確定性從(5)式中消去，利用文獻[9]引理2，以及Schur補引理進行化簡，類似于文獻[8]中定理2，可得如下線性矩陣不等式條件判定定理：

其中E(ε)，Z(ε)，A，B，D，Ea，Eb同上.

將含有時滯上下界的正定項在Lyapunov-Krasovskii函數中去掉，得到以上定理結論.相比于時滯依賴穩定性判據，雖未考慮時滯取值范圍，但簡潔可行，對任何時滯都可行，這是時滯獨立的穩定性判據的優越性所在.

將系統(1)除去不確定性F(k)，可易得以下推論：

其中E(ε)，Z(ε)，ΔA，ΔB，A，B同上.

2 算例

對帶有慣性環節的電力系統問題，建模成如下非標準情形的離散時滯奇異攝動不確定控制系統：

其中：

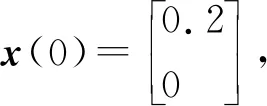
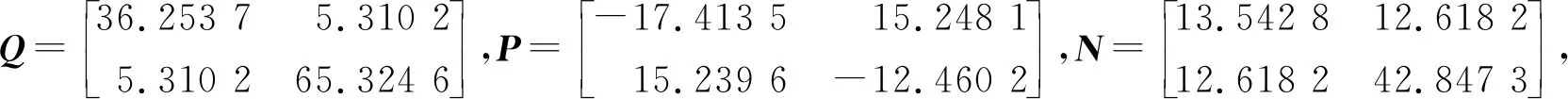
Z4=14.084 3，Z5=-18.346，γ=7.962 1.

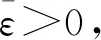
可見，?ε∈(0，6.152 3]，系統(1)漸近穩定.

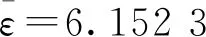
表1 算例穩定性數據分析

本算例說明了本文所得結論的優越性和可行性，進一步體現出在某種程度上，時滯獨立的穩定性效果更好.

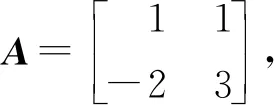
3 結語

(1) 本文是在文獻[8]基礎上的后續理論研究，其創新點在于，對比較復雜的離散控制綜合系統進行了時滯獨立情形下的穩定性研究，突顯了時滯獨立的理論特性及其優越點，可以為相關時滯獨立狀態下的魯棒控制問題研究提供理論參考.

(2) 基于連續的時滯系統中普遍涉及輸入時滯，而在離散的時滯系統中也存在輸入時滯的問題.因此，對于怎樣解決輸入時滯與離散系統之間的關系是需要進一步完善研究的課題.