環(huán)R{D，C}的Armendariz性質(zhì)

任艷麗，王 堯，周 昊

(1.南京曉莊學(xué)院信息工程學(xué)院，江蘇 南京 211171；2.南京信息工程大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，江蘇 南京 210044)

0 引言

本文所研究的環(huán)均指有單位元1的結(jié)合環(huán).設(shè)D是一個環(huán)，C是D的一個子環(huán)且1D∈C，令

R[D，C]={d1，…，dn，c，c，…|di∈D，c∈C，n≥1}，

R{D，C}={d1，…，dn，cn+1，cn+2，…|di∈D，cj∈C，n≥1}.

1 帶自同態(tài)的R{D，C}的性質(zhì)

證明只需證明結(jié)論(1)，結(jié)論(2) 類似可證.

充分性.設(shè)D是右α-可逆環(huán).由于C是α-不變子環(huán)，顯然有C也是右α-可逆環(huán).設(shè)

(a1，…，an，cn+1，cn+2，…)，(b1，…，bm，em+1，em+2，…)∈R{D，C}，

且

(a1，…，an，cn+1，cn+2，…)(b1，…，bm，em+1，em+2，…)=(0，0，…).

若n≥m，則有

a1b1=0，a2b2=0，…，ambm=0，am+1em+1，anen=0，cn+1en+1=0，cn+2en+2=0，…

由D和C是右α-可逆環(huán)知

biα(ai)=0，(i=1，2，…，m)，eiα(ai)=0，(i=m+1，…，n)；eiα(ci)=0，(i≥n+1).

于是有

(b1，…，bm，em+1，em+2，…)(α(a1)，…，α(an)，α(cn+1)，α(cn+2)，…)=(0，0，…)，

即有

證明只需證明結(jié)論(1).

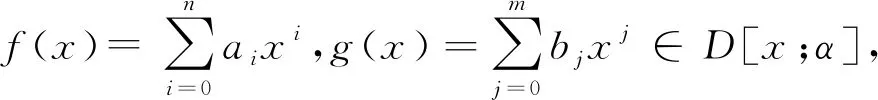
f(x)g(x)=0.

又由于

于是有

從而

證明只需證明結(jié)論(1).

由

2 環(huán)R{D，C}的其他性質(zhì)

稱環(huán)R為exchange環(huán)[2]，如果對任意的a∈R，存在b，c∈R，使得bab=b，c(1-a)(1-ba)=1-ba.

命題2.1S=R{D，C}是exchange環(huán)，當(dāng)且僅當(dāng)D和C是exchange環(huán).

證明必要性.首先注意到S=D1?C1，D1={(d1，0，0，…)|d1∈D}，C1={(0，d2，…，dn，c，cn+1，cn+2，…)|di∈D，n≥2，c，cj∈C}，顯然有D1?D，即D同構(gòu)于S的一個直和項(xiàng)，因?yàn)閑xchange環(huán)的直和項(xiàng)是exchange環(huán)，因此D是exchange環(huán).又由于有S=R{D，C}到C的滿同態(tài)φ：(d1，…，dn，cn+1，cn+2，…)c，exchange環(huán)的商環(huán)是exchange環(huán)，C同構(gòu)于S的一個滿同態(tài)像，于是C同構(gòu)于S的商環(huán)，從而C是exchange環(huán).

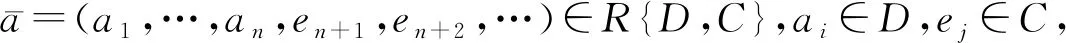
稱一個環(huán)R為強(qiáng)π-正則環(huán)，如果任意a∈R都是強(qiáng)π-正則元，即存在相應(yīng)的b∈R及正整數(shù)n，使得an=an+1b且ab=ba.

定義2.1 若對任意的a∈R，都有a或1-a是強(qiáng)π-正則元，則稱環(huán)R是幾乎強(qiáng)π-正則環(huán).如果環(huán)R/J(R)是強(qiáng)π-正則環(huán)，則稱R是feckly強(qiáng)π-正則環(huán).如果R/J(R)是幾乎強(qiáng)π-正則環(huán)，則稱R是feckly幾乎強(qiáng)π-正則環(huán).

命題2.2 環(huán)S=R[D，C]是feckly幾乎強(qiáng)π-正則環(huán)的充分必要條件是D是feckly強(qiáng)π-正則環(huán)且C/J(D)∩J(C)是幾乎強(qiáng)π-正則環(huán).

并且

稱環(huán)R是Armendariz環(huán)，如果對任意f(x)，g(x)∈R[x]，由f(x)g(x)=0可以推出aibj=0，?0≤i≤n，0≤j≤m.

定義2.2 稱環(huán)R是feckly Armendariz環(huán)，如果R/J(R)是Armendariz環(huán).

證明必要性.即要證明?i∈I，Ri/J(Ri)是Armendariz環(huán).取

這表明Ri(?i∈I)是feckly Armendariz環(huán).

命題2.4S=R{D，C}是feckly Armendariz環(huán)，當(dāng)且僅當(dāng)D是feckly Armendariz環(huán)，C/J(D)∩J(C)是Armendariz環(huán).

設(shè)I為R的一個非零右理想，若對R的任意非零右理想，都有I∩K≠0，則稱I為R的本質(zhì)右理想.記Zr(R)={x∈R|rR(x)為R的本質(zhì)右理想}，稱一個環(huán)R是右非奇異環(huán)，如果滿足Zr(R)=0.類似文獻(xiàn)[4]定理2.3的證明，可以得到：

引理2.1Zr(R{D，C})=R{Zr(D)，Zr(D)∩C}.

命題2.5R{D，C}是右非奇異環(huán)，當(dāng)且僅當(dāng)D是右非奇異環(huán).

證明由引理2.1，結(jié)論是顯然的.

設(shè)I是環(huán)R的一個理想，稱R中的冪等元模I可提升，如果a2-a∈I，則存在e2=a∈R使得a-e∈I.

命題2.6S=R{D，C}中冪等元模J(S)可提升的充分必要條件是D中冪等元模J(D)可提升，且C中冪等元模J(D)∩J(C)可提升.

稱環(huán)R是potent環(huán)[13]，若R中的冪等元模J(R)可提升，且R中不包含于J(R)的任意右理想都含有一個非零冪等元.文獻(xiàn)[13]引理1證明了上述定義是左右對稱的.

命題2.7 若S=R{D，C}是potent環(huán)且C的任意真理想是D的理想，則D和C是potent環(huán).

證明由于S=R{D，C}是potent環(huán)，于是S中冪等元模J(S)可提升，由命題2.6知D中冪等元模J(D)可提升，且C中冪等元模J(D)∩J(C)可提升.設(shè)ID為D的右理想，IDJ(D)，則有R[ID，0]J(S)，R[ID，0]為S的一個右理想.由S是potent環(huán)知存在非零冪等元(e1，…，en，0，0，…)∈R[ID，0]，因此必存在某個這推出D是potent環(huán).下證C也是potent環(huán).由于C中冪等元模J(D)∩J(C)可提升，于是C中冪等元模J(C)可提升.設(shè)IC是C的真右理想，ICJ(C)，于是ICJ(D)∩J(C).令則由題設(shè)知，任意C的真理想都是D的理想，于是為R{D，C}的一個右理想.由于S是potent環(huán)，存在中非零冪等元(0，0，…，ei，ei+1，…)，因此必然有某個C中的非零冪等元ej，從而C是potent環(huán).