基于小波閾值去噪與t-SNE的船舶柴油機故障識別

尚前明，沈 棟，邊祥瑞

(武漢理工大學 能源與動力工程學院，湖北 武漢 430063)

柴油機作為內燃機的一種，在船舶上的應用十分廣泛。作為船上重要的動力來源，人們對其工作的穩定性有著很高的要求。因為設備不可能一直處于正常的工作狀態，會出現各種類型的故障，所以對設備參數的監測與安全檢修、維護保養也是必要的。根據船舶柴油機常見的故障類型，其對應的故障診斷技術有很多，但基本以熱工參數[1，2]為主要診斷依據，其實船舶柴油機的機械振動信號中也蘊含很多的運行狀態信息，基于振動信號進行故障的分析與處理[3，4]有著很大的現實意義。

然而在處理振動信號時，由于原始信號中存在的噪聲信號容易對診斷結果產生一定的影響，故必須對其進行降噪。本文將采用小波閾值降噪的方法對振動信號進行降噪處理，然后利用不同工況下相同頻帶上振動能量不同的特點，將其作為特征向量，并結合部分時頻域的統計參數設計成一個特征集，使用t-SNE對特征進行降維處理，除去部分冗余的相關性小的特征量。最后使用支持向量機進行故障的診斷，求出識別率。經仿真實驗驗證，該診斷方案具有較高的識別準確率。

1 基本原理

1.1 小波閾值去噪

船舶柴油機在運轉時，其振動信號具有噪聲干擾大、非線性、非平穩的特點，所以在對其進行特征提取之前，需要對原始數據進行降噪處理。而小波變換有低熵性、時頻分析優良、多解析率和去相關性等特點，所以本文使用小波分析進行振動信號的非線性降噪。由于小波變換的去相關性特性，在經過小波變換后，信號之間就變得沒有關聯。也正是這種特性使得有效信號在經過小波變換后，能根據小波系數的不同區分出噪聲和能量的位置，從而再進行重構，獲得的新信號就是去噪后的信號。根據選擇的閾值不同，小波閾值去噪可分為硬閾值去噪和軟閾值去噪。小波閾值去噪步驟具體如下。

1)小波分解。選擇合適的小波基函數，確定需要分解的層次，然后對原始信號進行相應層次的小波分解，得到各層的小波系數。

2)閾值處理。用合適的閾值處理方式對分解后所得的高頻系數進行閾值處理。

3)小波重構。根據小波分解最后一層的低頻系數和經過修改的高頻系數，進行小波重構，得到降噪后的信號。

在小波變換后需要對所得的小波系數進行閾值處理，一般的閾值處理方式分為硬閾值函數處理和軟閾值函數處理。

(1)硬閾值函數：當小波系數w的絕對值小于給定閾值λ時，直接令小波系數為0；大于閾值時，則保持不變：

(1)

(2)軟閾值函數：當小波系數w的絕對值小于給定閾值λ時，直接令小波系數為0；大于閾值時，令其減去閾值：

(2)

1.2 t-SNE流形學習算法

t-SNE是Hinton等[5]基于SNE算法提出的一種新算法。它的核心是引入自由度為1的t分布函數代替高斯分布，構建高維空間數據樣本的概率分布，并在低維子空間構建對應樣本的概率分布，采用 KL 散度(相對熵)來衡量高低維空間的概率分布的相似程度，從而實現降維的效果。t-SNE算法降維的原理如下：在高維空間中，假定有N個數據樣本x，xi、yj為高維空間中任意2點，且xi的取值服從以xi為中心、方差為δi的高斯分布，同樣xj服從以xj為中心、方差為δj的高斯分布。首先計算xi和xj之間的條件概率pj|i和pi|j，進一步得到聯合概率pij。然后求取分布在低維空間中的yi和yj之間的聯合概率qij，使用KL散度來構造目標函數，使用梯度下降法來尋找高維樣本映射到低空間表達的最優解。

1.3 支持向量機

支持向量機[6]是1995年Cortes和Vapik提出的一種機器學習算法。其核心原理是利用映射函數將原始數據映射到高維空間，在高維空間內尋求一個分離線或分離面使樣本點間距離最大，從而達到樣本的分離[7]。SVM學習基本思想是求解一個分離超平面，使其能正確劃分訓練數據集且保證幾何間隔最大。作為一種二分類模型，支持向量機在具體使用過程中會結合數據樣本的特點選擇對應的核函數K(x,x′)和適當的懲罰參數C，用以構造目標函數并對其求解最優問題。為獲得最佳的核函數和懲罰參數，本文結合遺傳算法進行尋優。遺傳算法是模擬自然界生物遺傳的尋優算法，在進行交叉驗證方法條件下的準確率達到最高時，當下一組懲罰參數C和核函數K即為最優解，進行對測試集的驗證。優化后的GA-SVM算法流程圖見圖1。

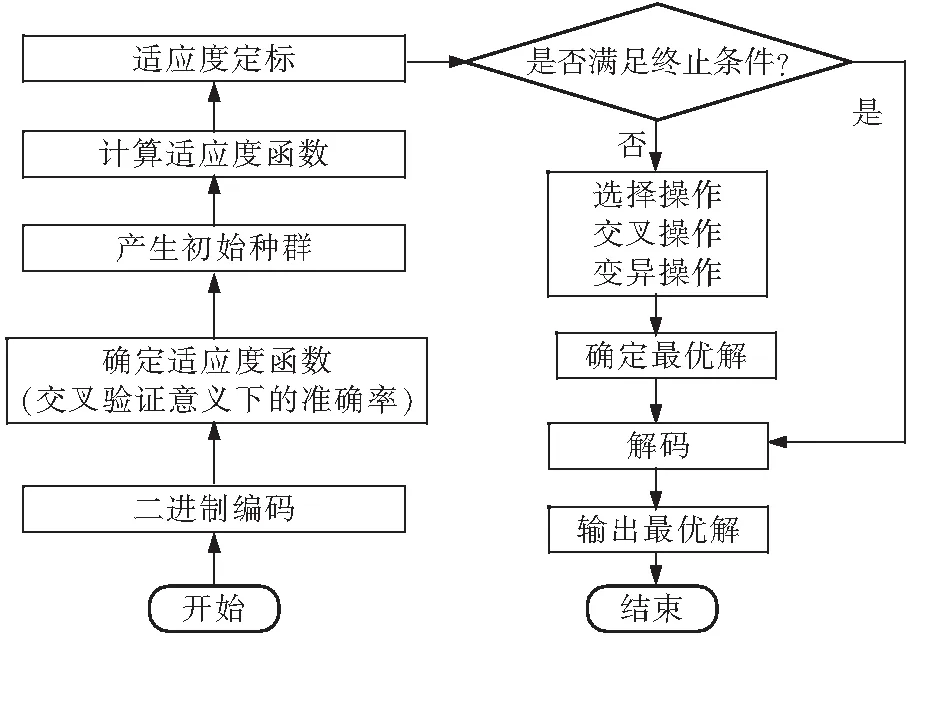
圖1 優化后的GA-SVM算法流程圖

2 故障診斷方法設計

由于不同的小波閾值去噪方法有不同的分析結果，本文提出一種將小波閾值去噪和t-SNE結合的故障診斷方法，最終選取出可以使用SVM判別故障類別的敏感數據集。具體步驟如下：①對振動信號進行小波分解，獲得各尺度的小波系數，對高頻的小波系數分別進行硬閾值處理和軟閾值處理；②針對2種閾值處理方式，計算信號的信噪比(SNR)和均方根誤差(RMSE)；③對比去噪信號圖像與原始信號圖像的相似度，以及SNR和RMSE的大小，找出最合適的小波閾值處理方式；④利用t-SNE對去噪后的特征數據進行降維，去除冗余不相關特征；⑤將降維后的低維特征數據分為訓練集與測試集，將訓練集輸入到GA-SVM中進行訓練；⑥用訓練好的GA-SVM對測試集進行分類，根據輸出結果確定故障類型并計算識別準確率。

3 應用與分析

為了驗證“故障診斷方法”中設計方法的有效性，利用實驗對其進行驗證分析。本文實驗數據是從實驗臺架采集得到的，該實驗臺架上的是YXR6110IZLD型柴油機，通過在1#缸的缸蓋上設置傳感器以獲得振動信號。對該柴油機分別進行了3種不同故障的模擬實驗，在40 kHz的采樣頻率和1 500 r/min的額定轉速下進行數據采集，并獲得實驗數據。故障類型及其模擬方式如表 1所示。

表1 故障類型及其模擬方式

3.1 小波閾值去噪與特征提取

對4種不同工況的樣本數據進行分析，將小波閾值去噪方法應用于樣本數據。選取本實驗柴油機一個工作循環中所采集的振動信號進行分析，取sym6為小波基函數，小波分解的層數為4。對樣本數據進行小波變換之后，使用不同的閾值處理修改高頻的小波系數，再進行信號重構獲得降噪后的信號，同時對比硬閾值處理和軟閾值處理方式對結果的影響，得到不同工況下軟、硬閥值處理后的SNR與RMSE對比如表2所示。

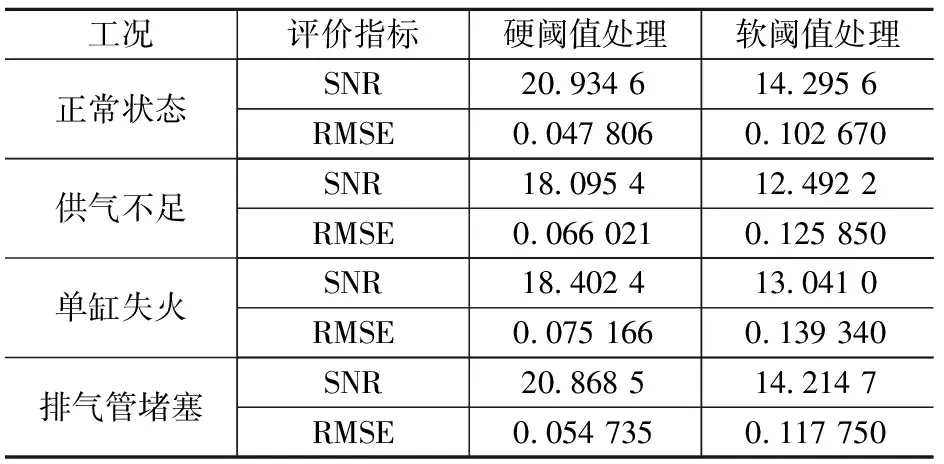
表2 不同工況下軟、硬閾值處理后的SNR與RMSE對比

由表2知，正常狀態、供氣不足、單缸失火和排氣管堵塞這4種工況下，信噪比的大小排列為硬閾值>軟閾值，而均方根誤差剛好相反。同時，硬閾值去噪處理后的信號與原始信號更加接近，保留的細節更多，由此得出在該實驗案例中，硬閾值處理方式優于軟閾值處理方式。

硬閾值處理后的信號進行小波系統重構，根據信號在16個頻段內的能量譜作出小波能量譜的特征向量圖，小波能量譜特征向量圖如圖2所示。實驗所測的4種工況的能量譜特征均值主要分布在頻帶5～16，且不同工況的能量分布不同，適合作為特征向量以區分不同的工況。

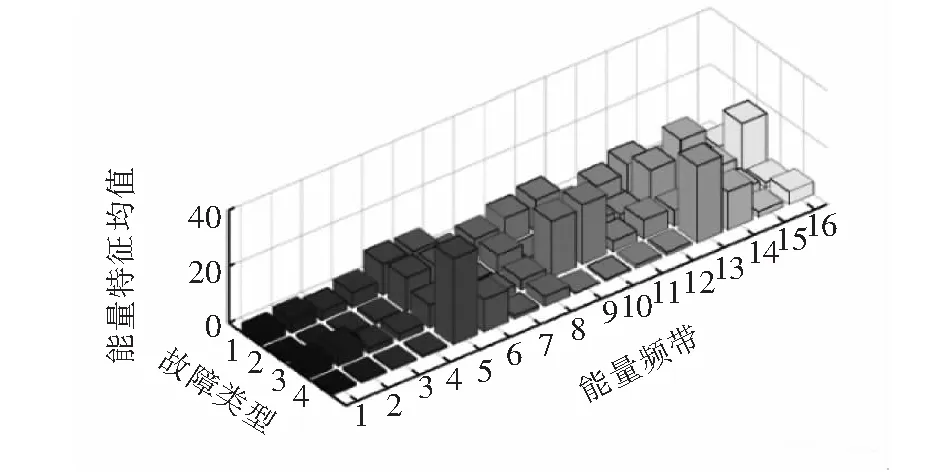
圖2 小波能量譜特征向量圖

3.2 特征降維與診斷結果

提取缸蓋上振動信號的均方根值、脈沖、波形、裕度、峰值和峭度等統計指標，與歸一化后的能量譜特征向量結合，形成新的特征向量。為減少后面GA-SVM的計算，提高診斷的效率，使用t-SNE進行降維，t-SNE和PCA的降維結果分別見圖3、圖4。如圖所示，t-SNE能將不同工況的樣本數據清晰地分開，降維效果較PCA好。

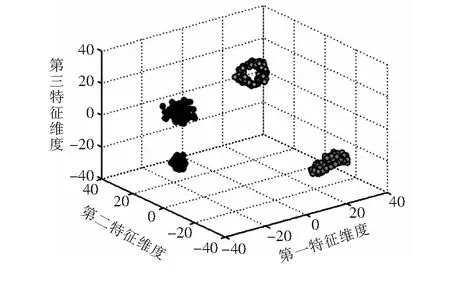
圖3 t-SNE降維結果

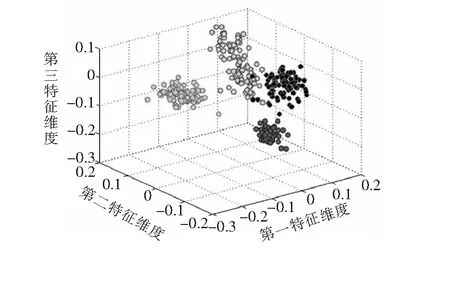
圖4 PCA降維結果

取使用t-SNE降維后的4種工況的特征數據用訓練好的GA-SVM進行分類，每種工況的20個樣本的測試集進行故障分類驗證。GA-SVM故障分類結果顯示，正常狀態、供氣不足故障、單缸失火故障和排氣管堵塞故障的故障識別準確率分別為100%、95%、100%和90%，均在90%以上。

4 結束語

針對船舶柴油機振動信號非線性和非平穩性的特點，本文提出一種基于小波分析和t-SNE算法結合的故障診斷方法，利用小波分解并進行閾值去噪，使用能量譜和一些時頻域統計量作為故障的特征向量，并對其進行t-SNE降維，最后使用GA-SVM進行故障的診斷。仿真實驗表明，本文提出的診斷方法具有較高的準確率，能有效地使用振動信號對船舶柴油機進行故障診斷。