基于偽柯西類核函數的主成分降維方法
劉文博,梁盛楠
(1.黔南民族師范學院數學與統計學院,貴州 都勻 558000; 2.黔南民族師范學院復雜系統與智能優化實驗室,貴州 都勻 558000)
0 引言
目前,諸多領域的數據呈現出高維度特點,即數據集包含幾百甚至幾千個變量,往往這些變量之間存在高度相關性且有些變量甚至與決策不相關.隨著變量數目的增加,更會產生所謂的“維數災難”[1],若直接利用機器學習算法進行處理勢必大量增加時間開銷.對高維數據進行降維、有效去除數據的冗余特征、降低特征之間的相關性是十分必要的.變量降維方法在基因表達數據識別[2]、圖像聚類[3]、機器學習[4-5]等領域起到了數據預處理的關鍵作用.
降維技術主要分為特征選擇[6]與特征提取[7].本文主要從特征提取的角度對高維基因表達數據進行維度約減研究,提高樣本類別的識別率.特征提取的典型代表為主成分分析法(Principal Component Analysis,PCA),其基本思想是利用較少的主成分(綜合變量)來替代原來較多的特征,而這些主成分能夠盡可能多地包含原始特征的信息,并且彼此不相關[8],PCA擅長處理線性、高斯型分布數據.但是,在很多情況下,數據往往呈現出非線性分布,若仍采用線性降維,則將丟失原本的低維結構.因此,一些非線性降維技術應運而生,其中最為典型的代表就是基于核技巧的非線性特征提取方法.如Scholkopf等[9]提出的基于核主成分分析(Kernel Principal Component Analysis,KPCA),該方法通過非線性映射將低維空間中線性不可分的數據映射到高維空間,實現高維空間中的線性可分.
核主成分分析的關鍵之處在于核函數的選擇,好的核函數可以更好地實現高維空間中樣本的線性可分.鑒于此,本文構造了一類新的核函數——偽柯西類核函數,對高維數據進行降維.通過在4個癌癥基因表達數據集的實驗分析,與全變量、高斯核、多項式核、雙曲正切核相比,在多數情況下,偽柯西類核函數的降維效果要優于傳統的核函數以及全變量情形.
1 核主成分分析
傳統的主成分分析可以較好地處理變量間的線性關系,但是當處理的數據呈現出非線性關系時,會導致各主成分貢獻率過于分散,不能找到有效代表原樣本的綜合變量,處理效果不夠理想[10].基于核技巧的主成分分析是一種較為理想的處理非線性問題的方法,其基本原理如下所述.
令原始樣本數據矩陣為
X=(xij)n×p,i=1,2,…,n;j=1,2,…,p.
其中:xi=(xi1,xi2,…,xip)′為數據集的第i個樣本,n為樣本容量,p為變量個數.
給定非線性映射Φ,將低維空間中的樣本映射到高維空間Y中,即
xi∈Rp→Φ(xi)∈Y.
在高維特征空間中利用主成分分析進行特征提取,使得原樣本空間中線性不可分數據在新空間下線性可分,如圖1所示.
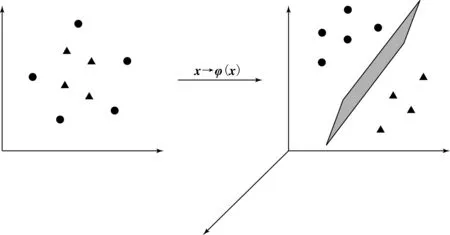
圖1 KPCA樣本分離原理示意圖
核主成分分析計算過程如下:
令zi=φ(xi)為xi在高維特征空間中的樣本,其協方差矩陣為
(1)
KPCA的求解目標為
(2)
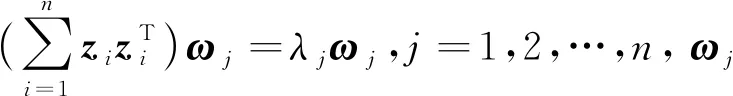
由于φ(x)形式一般未知,引入形式已知的核函數
κ(xi,xj)=φT(xi)φ(xj),
(3)
常用的核函數[11]:
(4)
(5)
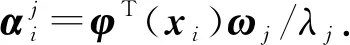
把(5)式帶入(4)式可得
(6)
將(6)式兩側同乘φT(X)=(φT(x1),…,φT(xn))T可得
Kαj=λjαj.
(7)
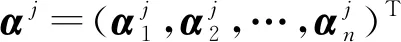
將(5)式帶入(2)式最終得到核主成分解
(8)
在進行維度約減時,一般取前d(d 核主成分的主要目標是基于核函數對數據進行維度約減,那么核函數選擇是否恰當就成為核降維的關鍵所在,這就需要不斷探尋新的核函數以提高核降維效果,以提高后續機器學習分類算法的預測性能.受到柯西核函數的啟發并依據如下定理1,本節構造新的偽柯西類核函數. 定理1[12]設f:X→R是有界可積連續函數,則k(x-x′)=f(x-x′)為核函數的充要條件是f(0)>0,且其傅里葉變換 定理2 令 (9) 則(9)式為核函數. 令t=-x,有 所以 因此 (10) 其中c>0,則(10)式為核函數. (11) 其中c>0,0 (9)—(10)式的表達形式與柯西密度函數較為相似,故本節構造的核函數稱之為偽柯西類核函數,將上述核函數應用于高維數據的特征約減,通過實驗分析將偽柯西類核函數與傳統核函數的維度約減效果進行對比. 利用本文構造的偽柯西核函數以及已有的高斯核、多項式核、線性核、雙曲正切核對真實數據集進行降維,然后采用目前主流的機器學習方法包括支持向量機(SVM)[13]、K近鄰[14](KNN)、樸素貝葉斯(NB)[15]在降維后的數據集與原始數據上進行分類預測,最后將不同核函數的降維效果進行對比研究. 實驗環境設置為:Windows10,64位操作系統,Intel i7-9 700、3.0 GHz CUP,16 GB內存,本文提出的算法和實驗基于R語言(R 3.6.3)編碼實現.使用來自Broad Institute Genome Data Analysis Center(http:∥portals.broadinstitute.org/cgi-bin/cancer/datasets.cgi)的4個真實癌癥基因表達數據集進行實驗分析,數據的基本信息如表1所示.為了評價不同維度下機器學習方法的分類性能,使用的性能度量指標為分類精度. 表1 數據集信息 基于核主成分分析的數據維度約減與分類識別步驟如下: ① 對數據集進行標準化處理,消除量綱的影響; ② 選取核函數以及設定核函數參數; ③ 依據步驟②的核函數計算核矩陣; ④ 計算核矩陣的特征值與特征向量并對特征向量進行歸一化處理; ⑤ 依據(8)式,計算原始數據在高維特征空間中的核主成分解yj,j=1,2,…,d; ⑥ 依據yj,j=1,2,…,d,利用機器學習分類方法對原始數據進行分類識別. 由于本文所使用的核函數均帶有參數,高斯核參數σ2,多項式核參數d,雙曲正切核參數β和θ,本文構造的偽柯西核函數(10)式中的參數c,需要對上述參數進行合理設定,即經過上述核降維后,使得后續的機器學習分類性能達到相對最優.由于每個核函數至多包含2個參數,在參數不多的情況下,采取較為適宜的網格搜索(Grid Search)策略,對每個核函數中的參數設定取值范圍并按等步長取值,使得后續分類算法達到精度最高的參數即為最終選取的參數.最終確定的參數分別為σ2=50,d=2,β=6,θ=-0.1,c=1.對比實驗結果見表2—4. 表2 基于全變量、高斯核、多項式核、雙曲正切核與偽柯西核的SVM五折交叉驗證精度比較 表3 基于全變量、高斯核、多項式核、雙曲正切核與偽柯西核的KNN五折交叉驗證精度比較 表4 基于全變量、高斯核、多項式核、雙曲正切核與偽柯西核的NB五折交叉驗證精度比較 根據表2給出的實驗結果可以看出,若不對原始數據進行降維,而直接應用SVM進行分類,在4個數據集上的精度僅有52%,31.88%,70%和19.33%,分類精度過低,這表明SVM對高維度小樣本數據集異常敏感,因此有必要對數據進行維度約減.經過核降維后,其分類精度有了明顯提升,與傳統的高斯核、多項式核和雙曲正切核相比,經過本文構造的偽柯西核函數降維后,SVM的分類精度達到最高分別為91.84%,98.79%,96.41%和98.05%.根據表3可以看到,偽柯西類核降維使得KNN的分類精度在Leukemia和Muliti-A數據集精度達到最高,在Breast和Lung數據集達到次最優.根據表4的結果,偽柯西類核降維使得NB在3個數據集上的分類精度達到最大,在1個數據集上精度達到次最大. 通過表2—4的實驗結果,總體上可以得出,與全變量、高斯核、多項式核以及雙曲正切核相比,經過偽柯西核類函數降維后可以使目前主流的機器學習方法如SVM、KNN和NB的分類性能有較為顯著的提升.這表明,核降維可以較為充分的提取原始數據集的信息.通過在4個癌癥基因表達數據上的數據分析,與傳統核函數相比,偽柯西核的降維效果要更為出色. 針對數據集高維度、高冗余性特點,為了提高后續機器學習算法的分類性能且能夠降低分類預測過程中的復雜度,本文提出一種基于偽柯西類核函數的主成分降維方法,即構造新的核函數對高維數據進行維度約減.通過在4個癌癥基因表達數據集的實驗分析,與全變量、高斯核、多項式核以及雙曲正切核相比,在多數情況下,偽柯西類核函數可更為有效地提高主流機器學習方法的預測精度.2 偽柯西類核函數
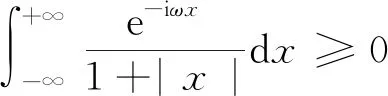
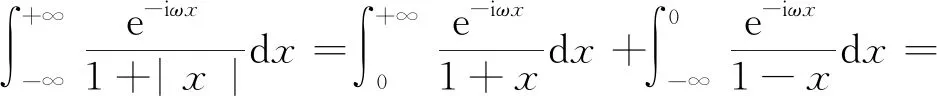
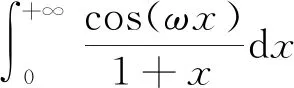
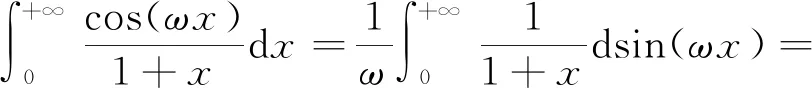

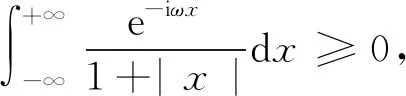
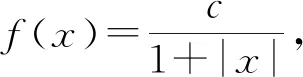
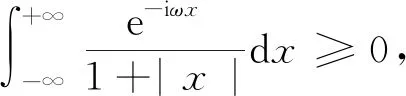
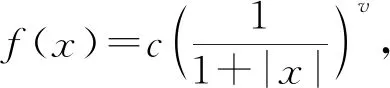
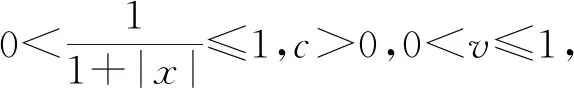
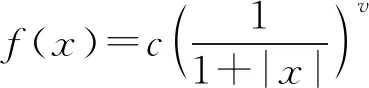
3 實驗結果與分析
3.1 實驗設計

3.2 對比實驗結果與分析



4 結論

