分數階次對分數階斜裂紋轉子系統的非線性動力學特性影響研究

陳玉成，李志農，谷士鵬，馬亞平

(1.南昌航空大學 無損檢測技術教育部重點實驗室， 南昌 330063; 2.中國飛行試驗研究院， 西安 710089)

1 引言

轉子在自身的服役期間，由于材料本身或工藝原因，在承受交變機械應力及熱場的作用下，非常容易形成疲勞裂紋。轉子在運行過程中，因扭轉振動會導致斜裂紋。斜裂紋故障在轉子的各項故障中占有較大比例，且其潛在危害遠大于其他一般性故障，是轉子系統正常運行的巨大隱患。目前，斜裂紋轉子系統的動力學特性研究雖然取得了一定的進展[1-6]。焦衛東等[1]對不同類型斜裂紋的轉子進行研究，揭示了在不同方向上的耦合機理及由此引發的振動特征；Sandeep[2]建立了主動磁軸承支承的含有裂紋故障的柔性轉子系統模型，分析其動力學特性；Xuelian Chen[3]用斜裂紋模型模擬軸裂紋引起的時變剛度，研究了偏心相位差對轉子系統動力學特性的影響；王崢[4]考慮裂紋故障引起的剛度變化，討論了裂紋轉子系統動力學特性；張祥敏等[5]分析了含斜線裂紋的非線性轉子系統隨裂紋角度和深度變化時的系統狀態變化。然而，現有的研究主要是建立在整數階的基礎上，并未考慮到斜裂紋轉子系統具有的分數階特性。因為分數階微積分具有記憶特性，所以描述具有記憶特征的阻尼材料時能更好地揭示對象的本質特性。基于此，眾多專家開始采用分數階微積分來研究斜裂紋轉子系統的動力學特性[7-12]。張順[7]研究含有裂紋與碰摩多種復合故障的分數階轉子系統，討論了系統偏心量與轉速對動力學特性的影響，并與整數階進行對比；李志農[8]、王海峰[9]等建立了直斜2種裂紋的動力學方程，研究了基于分數階的裂紋轉子系統非線性動力學特性薛士明[10]建立了帶有分數階阻尼的轉子系統動力學模型，研究了轉速和裂紋深度對裂紋轉子動態特性的影響；曹軍義等[11]建立了含有碰摩故障的分數階轉子模型，研究了該系統的非線性動態特性；王彥霖等[12]采用轉子動力學有限元方法建立含內部裂紋轉子系統的動力學方程，分析了裂紋的深度、裂紋的位置對轉子系統的影響。

這些研究主要考慮的是轉子系統中裂紋參數及轉速對系統非線性動力學特性的影響，并沒有討論分數階次的影響。基于此，本文中在建立了分數階斜裂紋轉子系統動力學模型的基礎上，通過數值仿真分析不同分數階次的斜裂紋轉子系統非線性動力學特性，為有效診斷斜裂紋轉子系統提供理論依據。

2 分數階斜裂紋轉子系統模型建立

本文建立的Jeffcott轉子模型如圖1所示，其中，R為轉軸半徑，Ω為轉軸的轉速，Ωt+α為在有扭振時轉盤轉角，t為時間。

圖1 斜裂紋轉子模型示意圖及截面z向投影圖Fig.1 Oblique crack rotor model and section z projection

在轉子系統中，斜裂紋是轉軸長期受到扭轉振動的影響生成的。因此，本文考慮到橫向、扭轉以及軸向方向的載荷建立了分數階斜裂紋轉子動力學方程。

具體的動力學方程如下所示：

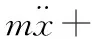
-mg+me(Ω+Drα)2cos(Ωt+α+φ)+

(1)

me(Ω+Drα)2sin(Ωt+α+φ)-

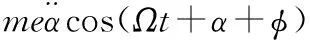
(2)

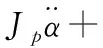
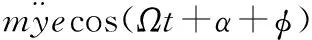
(3)

(4)

式中，各參數分別表示的是，M(t)為扭轉激勵；m為轉盤質量；Jp為轉盤轉動慣量；c為橫向振動方向的阻尼系數；x，y為兩橫向位移；cT為扭轉方向的阻尼系數；α為扭轉方向的扭轉角；cu為軸向的阻尼系數；u為軸向位移；e為轉盤的偏心距。

為了求解該動力學方程，需要事先確定系統的剛度。在固定坐標系下的剛度矩陣為[k]：

(5)

式中，kx、ky為兩橫向方向的剛度；kT為扭轉方向的剛度；ku為軸向方向的剛度；kxy、kxT、kyT、kxu、kyu和kTu則是各耦合方向的剛度。在實際應用中大部分的轉子系統一般很少受到軸向激勵的作用，所以式(4)沒有考慮存在軸向激勵力。

式(5)剛度矩陣[k]是采用應力強度因子為零法計算獲得的。

斜裂紋參數示意圖如圖2所示，在裂紋面上裂紋區域內的任意位置，總的第一應力強度因子KⅠ表示如下：

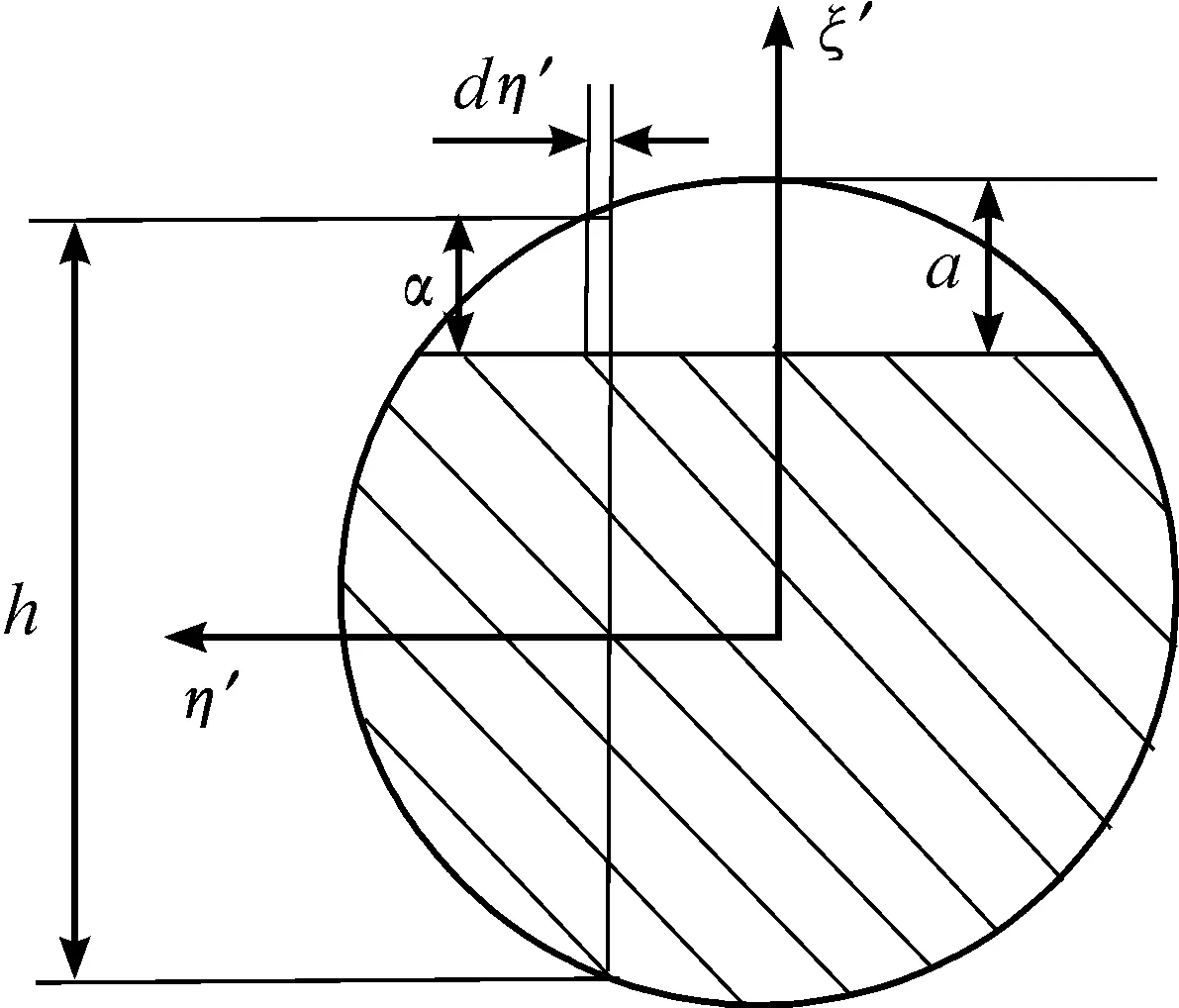
圖2 斜裂紋示意圖Fig.2 Schematic diagram of crack

KⅠ=KⅠξ′+KⅠη′

(6)

其中，KⅠξ′和KⅠη′為兩個方向的第一應力強度因子，分別為：

(7)

(8)

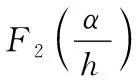
對含有裂紋深度為a，傾角為β的斜裂紋轉軸進行計算時，將轉軸沿垂直于Y軸的方向進行劃分。即可通過公式計算其在裂紋深度為a處的總應力強度因子為KⅠ和KⅢ。下列公式中E為彈性模量，v為泊松比；FⅠ、FⅡ、FⅢ為三項影響系數，能夠根據文獻[13]獲得。

由于該斜裂紋轉軸受軸向力q1，扭矩T和在X、Y兩個方向的彎矩q2和q3四個方向載荷的共同作用。可得在各載荷的影響下，該轉軸的應力強度因子如下：

對q1：

(9)

(10)

對q2：

(11)

對q3：

(12)

(13)

對T：

(14)

總應力強度因子為：

KⅠ=KⅠ1+KⅠ2+KⅠ3+KⅠ4

KⅢ=KⅢ1+KⅢ3

(15)

斜裂紋軸的能量釋放率密度函數為：

(16)

則裂紋轉軸釋放的應變能可表示為：

(17)

根據卡氏定理可得附加柔度為：

(18)

計算得到無裂紋情況下轉軸的柔度是：

(19)

斜裂紋軸的柔度為：

[c]l=[G1][Δc][G2]+[cs]

(20)

式中用到的轉換矩陣[G1][G2]分別為：

(21)

(22)

對式(20)求逆即可獲得該裂紋軸的剛度矩陣：

(23)

3 影響分析

本文研究在轉速和裂紋深度一定時，分數階次對動力學特性的影響。解方程所需各項參數具體如下所示，dp=76 mm；m=0.595 kg；L=0.46 m；d=9.5 mm；φ=π/6；ωT=0.6 Ω；E=210 GPa；v=0.3；c=41.65 kg/s；cT=0.009 1 kg·m2/s；cu=146.203 4 kg/s；Ω=300 rmp；α=d/2。

隨著分數階次的不斷增大，得到如圖3所示的系統響應分叉圖。

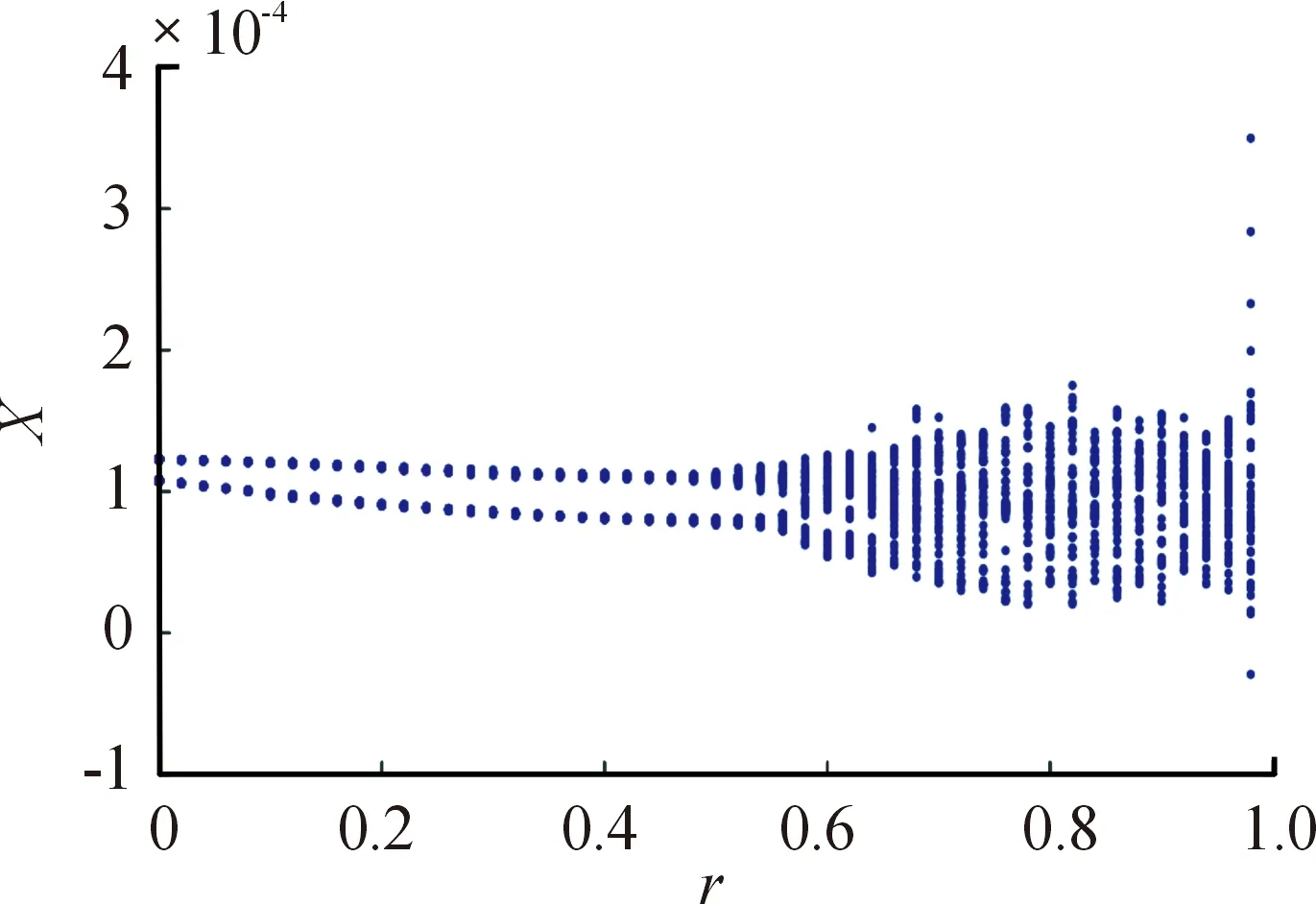
圖3 分數階阻尼階次分岔圖Fig.3 Bifurcation diagram of fractional order damping

從圖3可知，隨著分數階次的改變，系統的振動特性受到了很大的影響。當分數階次增大時，系統從倍周期運動狀態逐漸成為混動運動狀態。分別對r=0.2，系統處于倍周期運動狀態時；r=0.5，系統開始進入混沌運動狀態時；r=0.7系統徹底處于混沌狀態時3個階次進行數值分析。

當分數階次較小時，系統處于周期運動狀態，圖4為當r=0.2時的數值分析結果。軸心軌跡圖呈現典型的內8字形；相圖是表征擬周期運動的封閉圓環；Poincare不動點呈密集點狀出現，系統處于周期運動中；波形圖呈現規律的周期性；橫向頻譜圖中主要由不平衡量所造成的一倍頻成分和由斜裂紋造成的2倍頻成分組成；軸向頻譜圖包含1/2倍頻成分和相對比較弱的1倍頻成分。

圖4 r=0.2時軸心軌跡圖、相圖與Poincare截面圖、波形圖、橫向軸向頻譜圖Fig.4 The axis trajectory，phase diagram，Poincare section，waveform diagram，transverse axial spectrum(Frctional order r=0.2)

隨著分數階次增大，系統初步進入混沌運動狀態，圖5為當r=0.5時的數值分析結果。相比階次較低情況，軸心軌跡圖開始變得混亂，形狀較為模糊；相圖開始出現雜亂曲線；Poincare截面圖中不動點開始多次出現，系統逐漸脫離周期運動狀態；波形圖中幅值有所減小，同時出現了分岔諧波成分；橫向頻譜圖中1倍頻成分和2倍頻成分減小，由于轉軸受到的載荷作用，引起轉軸剛度出現耦合成分，進而導致橫向頻譜圖中開始出現其他低倍頻成分；軸向頻譜圖中的各倍頻成分幅值都有所減小。

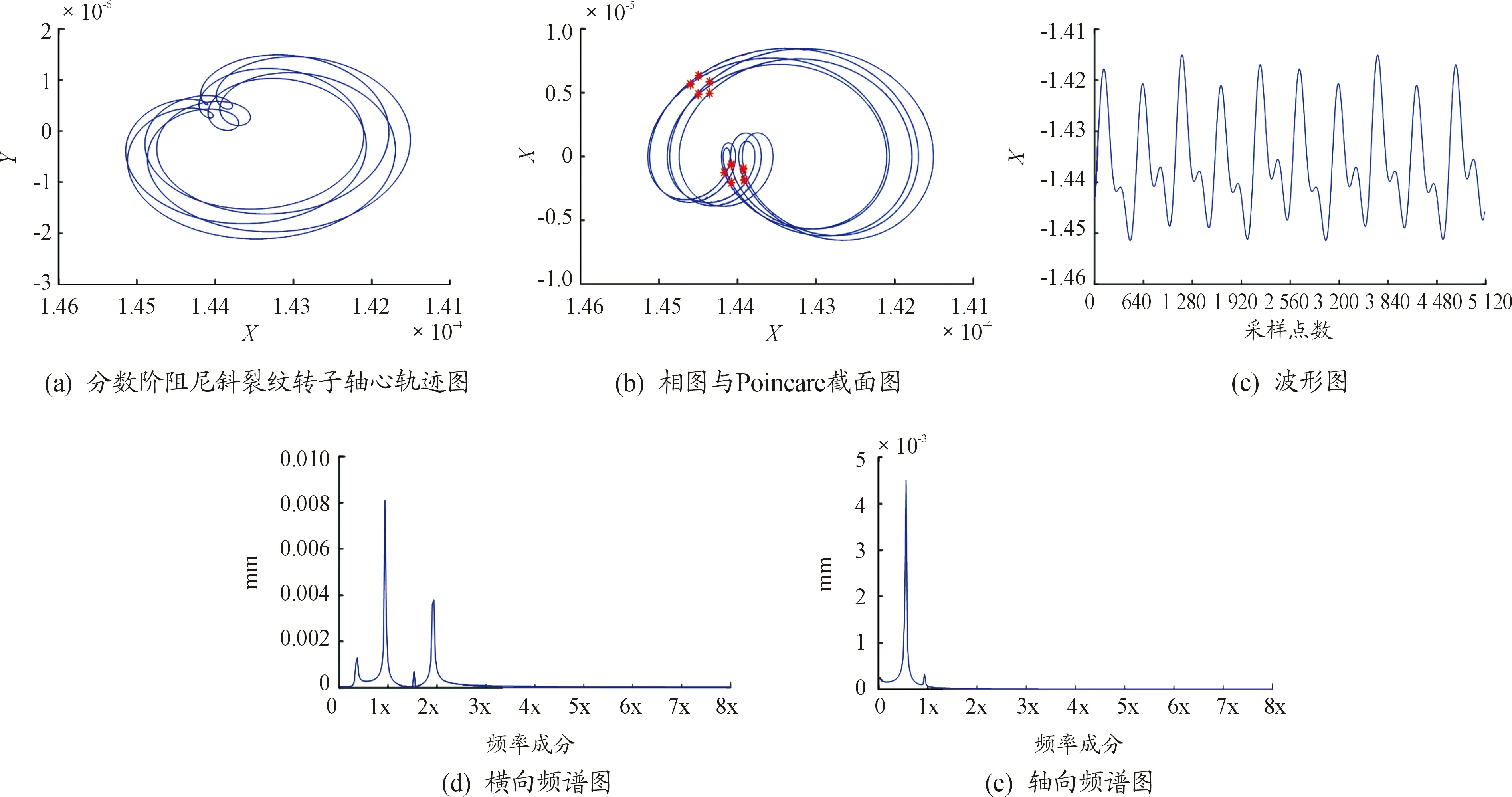
圖5 r=0.5時軸心軌跡圖、相圖與Poincare截面圖、波形圖、橫向軸向頻譜圖Fig.5 The axis trajectory，phase diagram，Poincare section，waveform diagram，transverse axial spectrum(Frctional order r=0.5)

當分數階次較大時，系統徹底進入混沌運動狀態，圖6為當r=0.7時的數值分析結果。可以看出此狀態下系統軸心軌跡圖混亂，不再呈現規則圖形；相圖中曲線混亂；Poincare截面圖中不動點開始大量出現，系統進入混沌運動狀態；波形圖中幅值進一步減小，諧波成分增多，不再呈現周期性；橫向頻譜圖中1倍頻和2倍頻成分幅值進一步減小，其他低倍頻成分幅值增大；軸向頻譜圖中的各倍頻成分幅值都進一步減小。

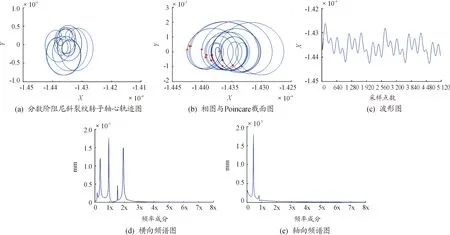
圖6 r=0.7時軸心軌跡圖、相圖與Poincare截面圖、波形圖、橫向軸向頻譜圖Fig.6 The axis trajectory，phase diagram，Poincare section，waveform diagram，transverse axial spectrum(Frctional order r=0.7)

4 結論

1) 當分數階階次r在增大過程中，轉子系統從倍周期運動狀態進入混沌運動狀態；這一過程中，斜裂紋轉子系統橫向頻譜中因扭轉激勵造成的頻率成分與耦合激勵造成的頻率成分幅值都隨之增大；軸向頻譜中的頻率成分都在減弱。

2) 分數階階次對分數階斜裂紋轉子系統的非線性動力學特性的影響十分明顯。在研究斜裂紋轉子系統時，采用分數階的動力學方程能更加詳細完整的描述轉子系統的動力學特性。在實際應用過程中可以選擇恰當的分數階次描述斜裂紋轉子系統不同狀態的非線性動力學特性。