基于hp-RPM的滑翔彈道優化及制導仿真
陸秋秋,易文俊
(南京理工大學 瞬態物理重點實驗室, 南京 210094)
1 引言
滑翔制導炮彈是一種由導航制導系統指揮飛向目標的無人駕駛飛行裝置。彈道優化是指在特定約束條件下,使導彈達到增加射程、保證精度等戰術指標的控制機制。
為了保證打擊威力,通常要求導彈在擊中目標時具有較大的落角。該類型的方案彈道的設計可以看作是一個帶有狀態約束、控制約束和終端約束的最優控制問題(optimal control problems,OCP)。在解決軌跡優化問題時,通常采用間接法和直接法這兩種數值方法。間接法將OCP轉化為Hamilton多點邊值問題的求解,從而獲得最優控制律,在早期的軌跡優化問題中得到廣泛的應用[1-4]。但是間接法很難求解復雜OCP中的兩點邊值問題,在實際的工程應用中受到限制,所以結構簡單、收斂快速的直接法成為當前軌跡優化問題的研究熱點。偽譜法(pseudospectral method,PM)是一種常用的求解最優控制問題的直接數值方法,它利用一組正交基在離散點對狀態變量和控制變量進行逼近,把連續時間內的最優控制問題轉化成為一個非線性規劃問題(nonlinear programming problems,NLP)來求解,具有高精度、高效率和全局性的特點,適用于現代數字計算機運算,在軌跡優化領域有著廣泛應用[5-7]。在偽譜法中采用網格自適應技術,根據某種誤差準則自動調整網格細化方式和插值多項式次數,可用較少的計算代價獲得較高精度的解,更適合狀態變量和控制變量曲率變化明顯的優化問題[8-9]。
由于計算誤差、模型誤差和外部干擾等因素的影響,導彈在實際飛行過程中的彈道有可能偏離預先計算的方案彈道。在實際飛行中,如何使導彈滿足既定目標的問題稱為導彈的再入制導問題,其核心是根據導彈的當前狀態在線生成一條可行的再入飛行參考軌跡,然后設計一種跟蹤此參考軌跡的強魯棒性的控制方法,以克服模型誤差、計算誤差和飛行過程中的外部干擾[10-11]。由于復雜作戰指標的要求,計算能力的提高,以及數值優化算法的改進,使得再入制導算法朝著實時在線、自適應的方向發展。
本文中對某型號滑翔制導炮彈在滑翔段的軌跡優化和再入制導問題進行了研究。采用舵偏角變化率作為控制變量,以最短滑翔時間為性能指標,利用hp-RPM方法設計了按一定落角打擊地面靜止目標的方案彈道。根據實際飛行過程中由于測量不準和陣風干擾造成的誤差,提出了一種基于hp-RPM方法的在線制導方案,實現了滑翔段最優控制律的在線生成。
2 滑翔彈道優化模型
為更好地描述滑翔段導彈的位置和姿態信息,同時為方便問題的研究,本文中僅考慮導彈在縱向平面內的運動,偏航平面內的運動可以用類似方法分析。在以上假設的基礎上,建立導彈在滑翔段的質心運動方程組:
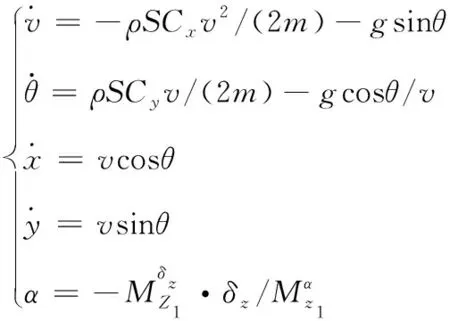
(1)
式中,(x,y)為導彈的位置坐標;v為導彈速度;θ為彈道傾角;S為參考面積;ρ為空氣密度;α為攻角;δz為舵偏角;Cx和Cy分別為全彈阻力系數和全彈升力系數。
彈道優化本質上是在各種參數約束條件下,通過尋找最優控制方式u(t),使導彈從一個狀態轉移到另一個狀態時的性能指標J最小(或最大)的非線性OCP,常用Bolza模型描述:
(2)
式中:x(t)∈Rn表示n維狀態向量;u(t)∈Rr表示r維控制向量;f(·)∈Rn表示n維狀態方程函數向量;J∈R是性能指標;Φ為終端性能指標;g為動態性能指標;φ為始端和終端約束函數;c為狀態轉移過程中參數約束。接下來,根據研究內容具體化Bolza模型中的各項參數和約束。
各種狀態變量在導彈飛行過程中的約束稱為狀態約束,在彈道起點和終點處的約束稱為端點約束。本文選取速度v、彈道傾角θ、水平距離x、飛行高度y和攻角α作為狀態變量。具體而言,為了確保導彈對地面目標的毀傷效果,必須限制導彈在終點時刻的速度和彈道傾角:
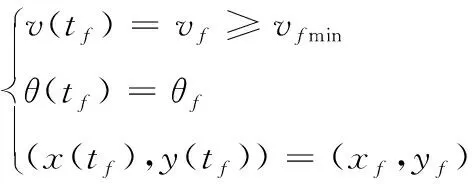
(3)
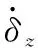
(4)
在滑翔過程中,除了狀態參數和控制參數以外的其他自定義參數需要滿足的約束都被稱為路徑約束。由于彈體強度有限,通常要求導彈的法向過載不超過限制值。此外,導彈的舵偏角也存在上限。路徑約束見式(5)和式(6):
|ny|≤nymax
(5)
|δz|≤δzmax
(6)
本文探究能在最短滑翔時間內命中固定目標的最優舵偏控制方案,其性能指標采用Mayer型表示:
minJ=tf
(7)
3 基于hp-RPM法的帶落角約束彈道優化
本文采用Radau偽譜法(RPM)將OCP問題轉化為NLP問題求解[12],并用hp自適應方法自動調整子網格的數目及網格內多項式的階數,既保證了計算精度,又提高了求解速度。
假定原OCP問題的定義域[t0,tf]被劃分成K個網格子區間[tk-1,tk],k=1,2,…,K,設x(k)(t)和u(k)(t)分別代表第k個子區間中的狀態變量和控制變量。因為Legendre方程的定義域是(-1,1),所以把變量t映射到τ∈[-1,1],轉換公式為:
(8)
3.1 牛頓迭代法求LGR離散點
分別用Nk+2次和Nk+1次Lagrange多項式插值來近似狀態變量和控制變量,即:
(9)
(10)
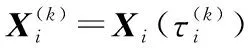
(11)
(12)
對式(9)求導以逼近原狀態方程的導數,有:
(13)

(14)

(15)
狀態變量在區間[t0,tf]內的邊界約束為:
(16)
狀態變量在飛行過程中的路徑不等式約束為:
(17)
3.2 hp網格自適應配置
本節給出一種hp網格自適應調整策略,該策略根據自定義的誤差評估準則來判斷網格是否需要細分或增加多項式階數。當網格子區間的誤差超出允許范圍時,需要調整網格的數目、網格的長度或多項式階次,以提高求解精度。

(18)
(19)
則動態約束方程和過程約束方程在上述采樣點的近似誤差估計為:
(20)
(21)

(22)
(23)
定義第k個網格內的誤差最大值為:
(24)
各項目單位每月至少開展1次活動,一年開展不少于12次活動;活動類型不少于3種;每種類型活動不少于4次;每個小組活動不少于4節。
若第k個網格內精度不滿足要求,需根據曲率決定是否細分該網格或增加其中的多項式階數,定義第k個網格子區間內各點的曲率為[15]
(25)

(26)
設置rmax>1為用戶自定義的容忍相對曲率,若r(k)≥rmax,說明這一段網格內的曲率變化較大,需將該網格劃分成更小的子區間,將第k個網格分成nk個更小的網格子區間的計算方法為:
(27)
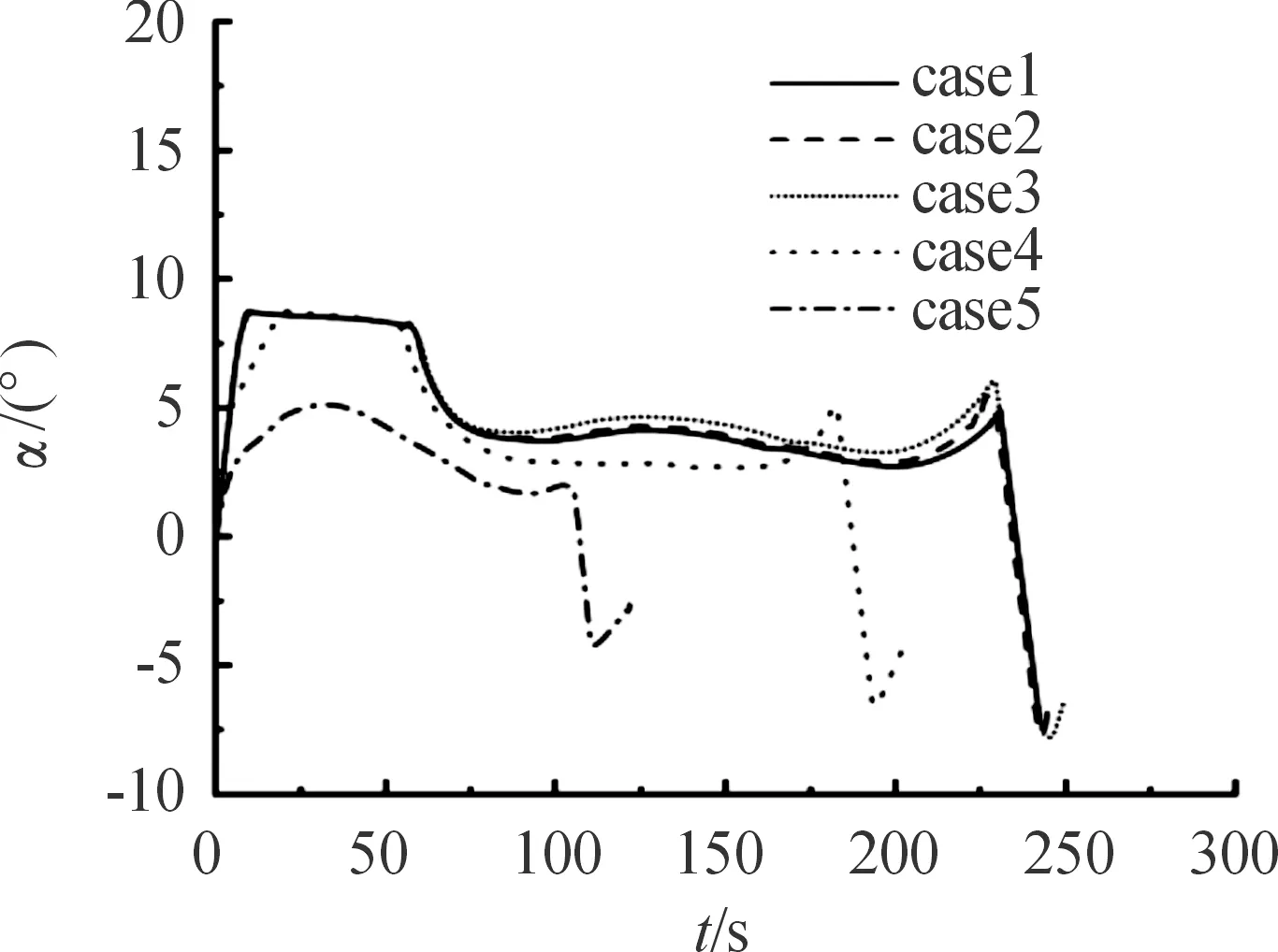
如果r(k) (28) 根據戰術指標和發射條件,可以離線求解導彈的最優軌跡和控制量變化規律。導彈在實際飛行過程中直接依據離線控制律進行導引的方法稱為開環制導。但是由于模型參數誤差和外部干擾等不確定性因素的影響,導彈的實際軌跡和各項彈道參數往往會偏離基準彈道。本文提出的在線閉環制導策略中,測量系統獲得當前制導周期初始時刻的實際彈道參數,并以此為初始值在線生成下一個制導周期的控制規律,當前制導周期的長度由hp-RPM算法的運行速度決定,反饋制導的具體步驟如下: 1) 假設t0為初始時刻,x0=x(t0)為初始狀態變量,選定初始迭代網格數目和多項式次數后,利用hp-RPM方法離線計算出開環最優控制律u0。 3) 假設ti為測量系統第i次采樣時刻,在時間[ti-1,ti](i=2,3,…)內,用控制律ui-1控制導彈的飛行,并記錄ti時刻彈丸各項狀態變量為xi=x(ti)。以xi作為新的初始狀態,利用hp-RPM方法更新剩余彈道的控制律ui,假定優化程序的運行時間為Δti,則下一次測量系統采樣時間即為ti+1=ti+max[Δti,1],令i=i+1。 4) 判斷導彈是否擊中地面某目標,若未擊中,則返回步驟3);否則,退出循環。 以某型號滑翔制導炮彈為例,采用hp-RPM方法設計了帶落角約束方案彈道。導彈的質量為50.31 kg,參考面積S=1.327×10-2m2,發射的初速度v0=400 m/s,投放坐標(x0,y0)=(0 km,20 km),彈道傾角θ0=0 rad,攻角α0=0 rad。該型號導彈部分氣動參數如表1所示。 表1 氣動參數 表2 終端約束 實驗結果如圖1~圖6所示。根據傳統最大升阻比法可計算得到相同發射條件下,該型號導彈的最大射程為7.526×104m,由圖1~圖3,在導彈最大射程范圍內,hp-RPM方法適用于以不同落角精確打擊不同距離處地面靜止目標的優化彈道設計,同時能滿足飛行過程中的過載限制。 圖1 不同終端約束下基準彈道的軌跡曲線Fig.1 Trajectory curve of reference trajectory under different terminal constraints 圖2 不同終端約束下基準彈道的彈道傾角曲線Fig.2 Trajectory inclination angle of reference trajectory under different terminal constraints 圖3 不同終端約束下基準彈道的過載曲線Fig.3 Overload of reference trajectory under different terminal constraints 控制系統在導彈的滑翔段操縱舵翼偏轉,實現對飛行姿態的有效控制,圖4為理想狀態下基準彈道的舵偏角的變化曲線,由于實驗中以最短滑翔時間為性能指標,故舵翼在進入滑翔段后立刻充分偏轉,使導彈獲得較大攻角,極大減緩導彈速度的衰減速度,使導彈按較小的彈道傾角和較大速度迅速逼近目標,達到短時間內擊中目標的目的。在滑翔段的中期,舵偏角變化平緩,有利于方案彈道的實現。由于對彈道末端的落角存在約束,在導彈接近目標時,舵翼產生反向舵偏角,使彈頭向下傾斜,從而獲得較大落角,如圖4~圖6所示。 圖4 不同終端約束下基準彈道的舵偏角曲線Fig.4 Rudder deflection curve of reference trajectoryunder different terminal constraints 圖5 不同終端約束下基準彈道的速度曲線Fig.5 Velocity curve of reference trajectory under different terminal constraints 圖6 不同終端約束下基準彈道的攻角曲線Fig.6 Attack angle curve of reference trajectory under different terminal constraints 假設導彈的升力系數和阻力系數由于模型誤差的存在±10%的波動,且導彈在發射后50~100 s內受0~50 m/s的陣風干擾。導彈的發射條件和路徑約束與4.1節中的實驗相同,終端約束為αf=-85°,定點打擊坐標位于(60 km,0 km)處的靜止目標。分別采用開環控制和本文提到的閉環制導方式進行仿真實驗,硬件環境為Core i7處理器,16.0GB RAM,軟件環境位64位Win10操作系統,Matlab R2018a軟件,實驗結果如圖7~圖10所示。 圖7 開環和閉環控制下的彈道軌跡Fig.7 Trajectory under open-loop and closed-loop control 圖8 開環和閉環控制下的速度曲線Fig.8 Velocity curves under open and closed loop control 圖9 開環和閉環控制下的彈道傾角曲線Fig.9 Trajectory inclination curves under open-loop and closed-loop control 圖10 開環和閉環控制下的過載曲線Fig.10 Overload curves under open and closed loop control 由實驗結果可知,相比于陣風影響,±10%的氣動參數波動對彈道各項參數影響不大。若采用開環控制,將離線設計的最優控制律u0直接應用于控制系統,導彈在50~100 s間由于受到陣風影響,將明顯偏離基準彈道,彈道傾角顯著減小,導彈提前擊中地面,無法準確命中目標。 表3中為開環控制和閉環控制仿真實驗的終端參數,發現由于模型參數誤差和陣風干擾的存在,使開環控制下的導彈在終點時刻,與目標水平相距1.977 km,且落角為-23.23°,不能滿足作戰需求。若采用基于hp-RPM的閉環制導方式,則導彈在終點時刻的位置橫坐標為59 981.06 m,與目標近相差18.94 m,打擊精度得到很大提高,能滿足一般作戰需求。閉環制導下的實際彈道落角為-85.46 °,飛行時間為202.23 s,與基準彈道的落角和滑翔時間相差不大,基本可以實現預設的快速、大落角、精準打擊的作戰指標。 表3 開環和閉環控制下的終端參數 采用hp-RPM方法設計在不同作戰指標下的制導炮彈滑翔段的方案彈道和在線制導策略。通過仿真實驗分析了滑翔彈最短滑翔時間和落角控制的作用機制,證實了基于hp-RPM方法的閉環在線制導策略能有效抑制模型誤差和外部擾動,實現既定的作戰指標。由于系統的控制周期由程序優化計算時間決定,所以對誤差的抑制能力與計算機的計算能力相關。 本文中的研究結果可為滑翔制導炮彈制導律設計提供參考,具有工程應用價值。4 基于hp-RPM的在線制導策略
5 仿真實驗結果
5.1 方案彈道實驗
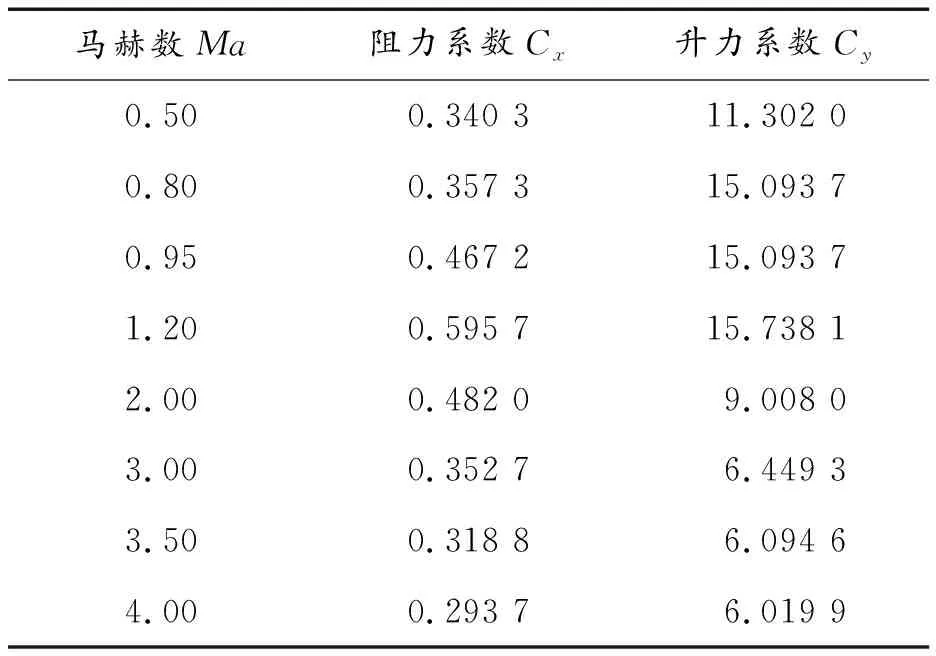






5.2 滑翔彈道再入制導





6 結論

