無力條件下的磁陀星扭曲磁場

張銘浩，余 聰

(中山大學 物理與天文學院，廣東 珠海 519082)

磁陀星是宇宙中磁場最強的一類中子星，也是目前人類發現的宇宙中磁場最強的一類天體.磁陀星外部磁層的行為由磁壓所主導，等離子體壓強可忽略不計，因此適用無力條件.本文從無力條件出發，通過自相似假設將Grad-Shafranov方程化為變量分離形式，從而簡化計算，得到了Grad-Shafranov方程的數值解，并依此給出了不同電流參數下的磁場線投影圖、三維磁場線圖，并通過數值積分得到了磁場線偏轉角以及磁能隨電流參數的變化關系.

1 無力磁場模型

1.1 無力場的靜力學條件

無力場是磁流體力學中的一個概念.當磁場的磁壓強遠大于等離子體壓強的情況下，等離子體壓強可以被忽略而只用考慮磁壓強.從靜力學平衡角度分析，在磁場足夠強的區域中，帶電粒子受到洛倫茲力的量級遠大于壓力梯度、重力以及慣性力的量級，從而靜力學平衡關系簡化為洛倫茲力為零，故該條件被稱為“無力條件”.在該條件下，電流密度只有平行于磁場方向的分量.

在求解黑洞磁層、太陽日冕磁場等以磁壓強為主導的很多高能天體物理問題時，無力磁場模型均能給出合理的結果.本文研究的磁陀星是中子星中具有最強磁場的一類，也是目前宇宙中已知的具有最強磁場的一類天體，因此是適用無力磁場模型的典型代表.

1.2 電流為零時磁場為有勢場

由于我們研究處于穩態的磁層，高斯單位制下麥克斯韋方程組的全電流定律

退化為靜磁場的安培環路定理

(1)

式(1)給出了靜磁場磁感應強度與電流的關系.若電流密度J為0，可知該磁場無旋，故可寫為一個標量函數(磁標勢)的梯度

B=-φ

1.3 電流不為零時的磁場與Grad-Shafranov方程

1.2節中的磁標勢是描述磁場的常用方法，其負梯度方向為磁場方向. 除了用磁標勢φ，軸對稱磁場還可以用流函數ψ(r,θ)來普遍表達：

(2)

磁標勢φ的等值線為等勢面，與場線處處垂直；而流函數ψ的等值線即為場線. 若電流密度J不為0，將無力條件：

代入安培環路定理(1)可以得到磁場的流函數滿足如下方程[2]：

×B=α(ψ)B

(3)

由于穩態和軸對稱性的要求，無力系數α是ψ的函數.

在球坐標系中，滿足式(3)的微分方程用磁場流函數的形式可寫為

(4)

其中I(ψ)為流經磁場線ψ的總電流強度.

由式(4)給出的磁場的繞極軸旋轉的分量為

(5)

對式(4)做變量替換μ=cosθ，則式(4)化為Grad-Shafranov方程的形式：

(6)

(7)

式(7)是線性方程，可以變量分離. 不難驗證單極子、偶極子、四極子等軸對稱極向磁場都滿足式(7).

由于磁陀星磁場足夠強，可以對殼層施加足夠的應力導致殼層剪切，從而使磁場扭曲. 要研究其扭曲磁場的位形，我們只能對式(6)進行求解.

2 對扭曲磁場的數值求解

2.1 自相似假設下扭曲磁場本征值問題的求解

與可變量分離的式(7)不同，式(6)是非線性方程，求解二維非線性偏微分方程非常困難. 人們采用自相似的假設，并在太陽物理、強磁星的研究中取得了和觀測吻合的結果. 我們同樣采用自相似假設，認為滿足式(6)待求磁場的流函數可以變量分離[2]，即ψ可以寫成只含有r的部分與只含有μ的部分之乘積：

ψ=R(r)F(μ)

并假設流函數關于r的部分為冪函數形式[2]：

R(r)=r-p

討論電流強度滿足流函數ψ的冪函數的形式：

(8)

其中C，p為待定參數. 則式(6)可化為變量分離的形式：

R(r)=r-p，

(9)

接下來的工作只需找到滿足式(9)的解F(μ)，即可對上述假設下磁場的性質進行討論. 我們注意到式(9)是二階常微分方程. 一般情況下，二階常微分方程只需要兩個初始條件即可確定. 而式(9)的求解是一個本征值問題. 因此我們需要找到合適的C、p值，使得式(9)的解剛好滿足給定的3個邊界條件.

我們用流函數重新表述球坐標系下磁場的3個分量，并給出在實際情況下偏微分方程(6)所滿足的邊界條件

注意到

做變量替換μ=cosθ后可以得到磁場3個分量與r、μ的關系

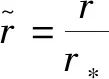
(10)

(11)

(12)

方程第一個邊界條件要求在極軸上Bφ=0，即

F(1)=0

第二個邊界條件要求在極軸與星體表面交點處的磁感應強度恒為B*，即

F′(1)=-2

F′(0)=0

我們采用“打靶法”解決上述本征值問題. 利用 第一、第二個邊界條件，從μ=1處開始積分，找到滿足第三個邊界條件的解對應的C，p值. 圖1給出了滿足上述三個邊界條件的參數C與p的關系. 可以看出在p=0.63附近，C達到最大值0.8732.

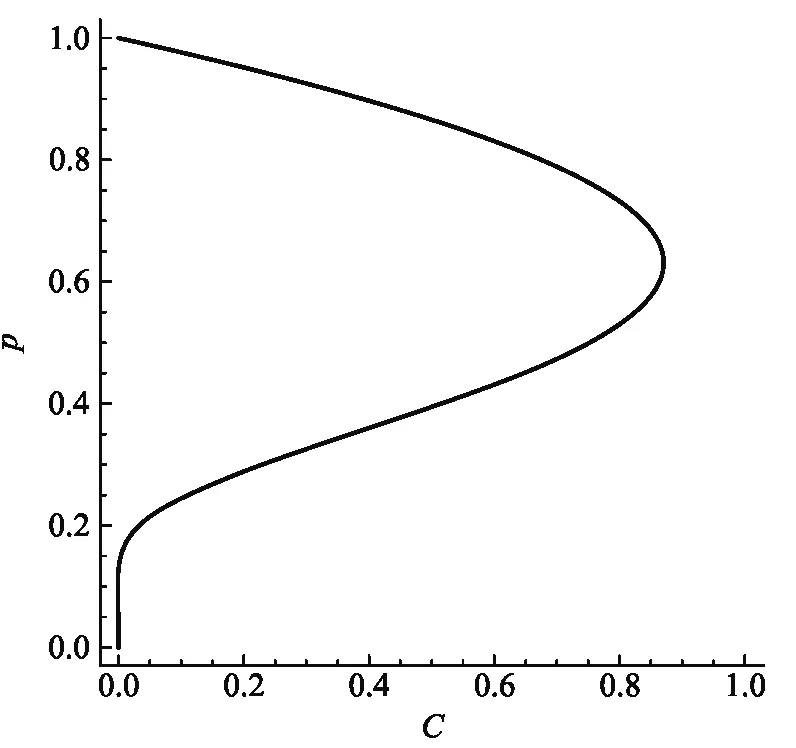
圖1 滿足式(8)邊界條件的C與p的關系

圖2給出了數值求解微分方程(8)得到的解F(μ)在不同C,p值下的函數圖像.可以發現在p→0時,除了在μ=0附近，F(μ)→2(1-μ).

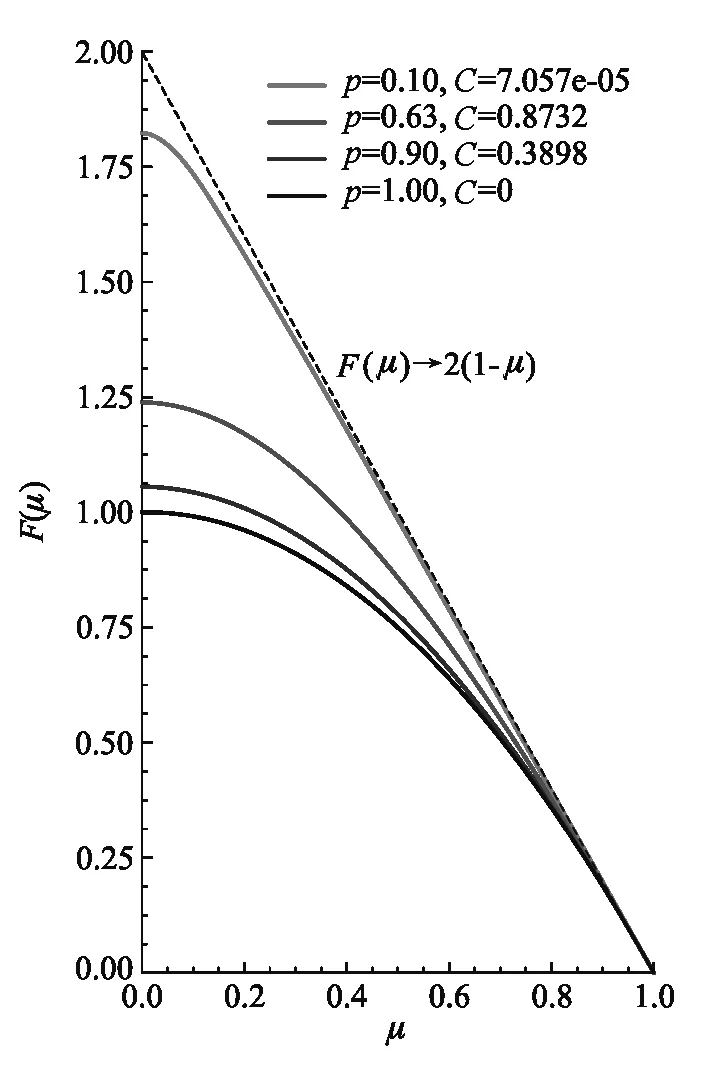
圖2 不同p值下的式(8)的解F(μ)

2.2 磁場線的繪制與對上述解的討論

圖3 磁場等值線圖

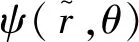
圖4 磁場線在r-θ平面的投影以及扭曲情況

3 求解磁感線的偏轉角

在電流參數C≠0時，根據矢量與其積分曲線的關系，我們有

從磁感線在星體表面的起始位置到終止位置對dφ積分，可得到偏轉角Δφ.根據積分上下限選取的不同，我們會得到不同的偏轉角

(13)

作變量替換μ=cosθ，從而積分化為

選取不同θ值作為磁感線在星體表面的起(止)位置，對上式數值積分，分別作Δφ與C，p的關系，得到圖5的結果. 可以看出隨p減小，在C達到最大值前，各位置起止的偏轉角Δφ均隨C的增大而增大；在C達到最大值后，N-S極附近起止的磁感線偏轉角Δφ隨C的減小而增大，赤道附近起止的磁感線偏轉角Δφ隨C的減小而先增后減.

圖5 偏轉角Δφ在不同θ值下與參數的關系

其中圖5(a)、圖5(b)中黑色加粗線為起止點在N-S極(θ=0)處磁場線的扭曲情況Δφ(θ=0)，即為磁場線的最大偏轉角. 由圖5(a)可以看出：在電流參數C取最大值0.8732時，磁場線的最大偏轉角在1.8 rad附近.由圖5(b)可以看出：隨p值增大，N-S極磁場線的偏轉角趨于π,該結果與文獻[2]給出的結果一致.

作Δφ-θ圖，得到在不同電流參數下，偏轉角與磁感線在星體表面起止點位置θ的關系，如圖6所示.可以看出在同一電流參數下，越靠近兩級的磁場線偏轉角度越大，這說明磁場線在兩極處的扭曲比赤道附近更明顯，該結論與圖4給出的結果是一致的.

圖6 偏轉角Δφ與磁感線起點位置的θ值的關系

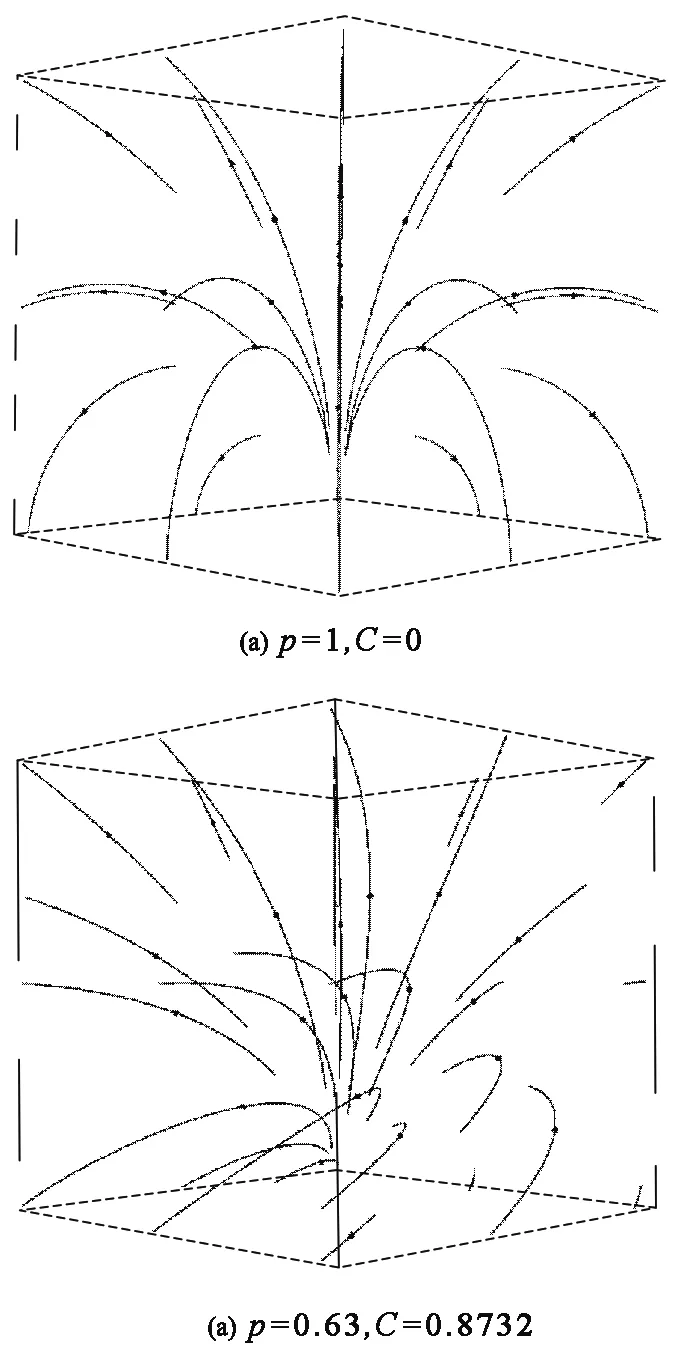
圖7 三維磁場線

4 計算磁陀星磁能隨磁場扭曲的變化關系

在高斯單位制下，對磁場能量密度在除星體外的全空間進行積分，可得到磁陀星磁場能量E：

(14)

寫為分量形式：

由于我們討論的解可以變量分離，上述積分可以化為以下形式：

取不同的C、p值，對以上3式進行數值積分并求和，可得到磁陀星磁場能量隨參數C以及起止點N-S極的磁感線偏轉角度ΔφN-S的關系. 取偶極子情況的磁場能量Edipole為1，根據積分結果繪圖，磁場能量與偏轉角ΔφN-S的關系如圖8(a)所示；磁場能量與電流參數C的關系如圖8(b)所示. 由圖可知磁陀星磁能隨磁場N-S極偏轉角增大而增大.

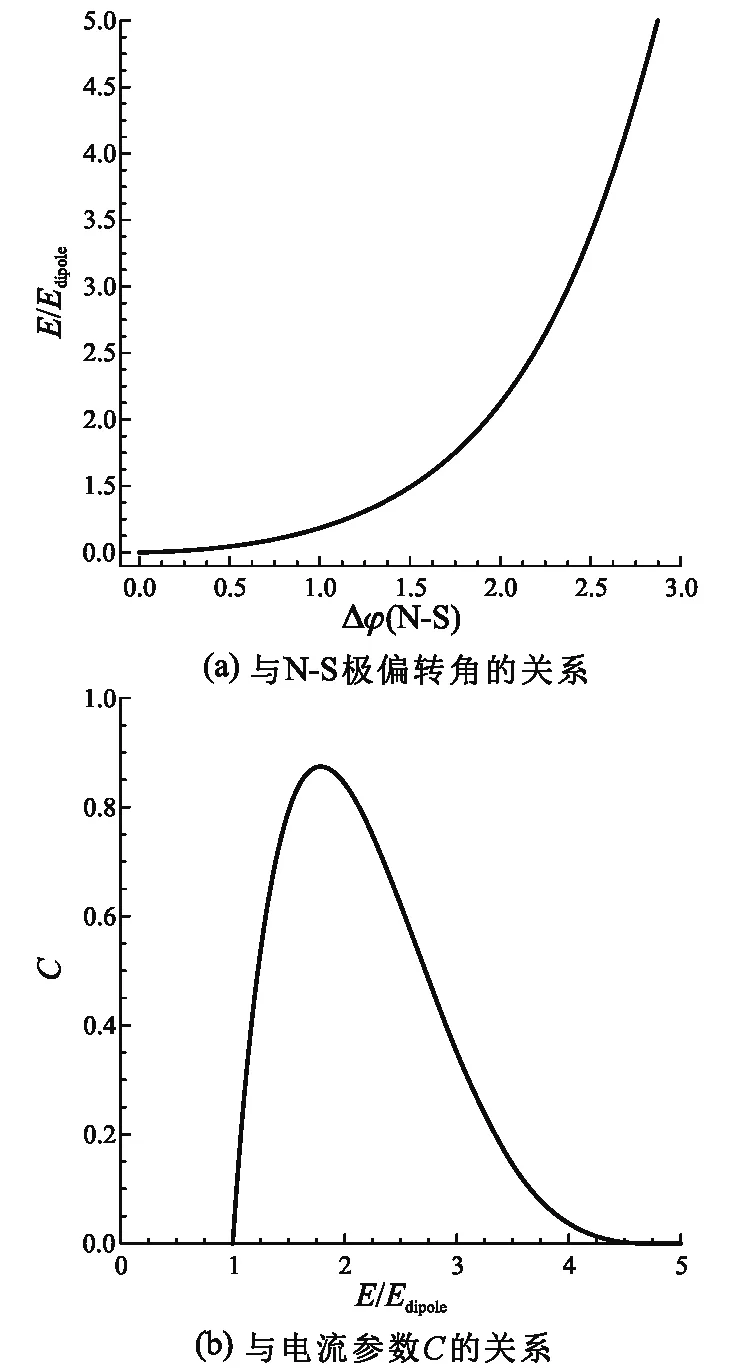
圖8 磁陀星磁能的變化關系

5 總結

Grad-Shafranov方程的變量分離解能夠給出在一定近似條件下的磁陀星附近磁場的性質.本文首先從無力條件出發，在自相似假設下數值求解了變量分離的Grad-Shafranov方程，得到了磁場的流函數解，并由該解繪制了磁感線、磁感線偏轉程度隨電流參數的關系.隨后通過數值計算得到了偏轉角，并探討了偏轉角與磁感線起止位置、電流參數的關系，得到兩極附近起止的磁感線偏轉角度大于赤道的結論，給出了磁感線的三維模擬圖.以上結果與其他文獻中基本一致.最后通過對磁場能量密度積分計算磁能，通過數值計算給出了在本文假設下的星體磁能隨偏轉角以及電流參數的變化關系，得到磁能隨N-S極偏轉角增大而增大的結論.

本文雖以自相似假設出發，但得到的結果依然 能夠反映出磁陀星磁場的一些關鍵性質.基于本文的計算可以對磁陀星的磁場演化做進一步的研究.