洛倫茲變換的低速近似

魏益煥，齊曉華

(渤海大學 物理科學與技術學院，遼寧 錦州 121000)

洛倫茲變換的提出先于狹義相對論建立的時間.1892年，洛倫茲提出了長度收縮假說；1904年，洛倫茲在《運動物體小于光速的電磁現象》一文中提出了洛倫茲變換.在狹義相對論建立之前，洛倫茲變換的出現還只是為了解釋一些特定的物理現象，它否定的僅僅是伽利略變換的形式，并沒有完全突破牛頓時空觀的框架.在狹義相對論中，洛倫茲變換是兩個基本原理所導致的一個結果[1].

相對性原理的內涵依賴所適配的時空坐標變換的形式.時空坐標變換的性質反映時空的幾何結構.在牛頓時空中，慣性系之間的時空坐標變換為伽利略變換.在狹義相對論時空(四維閔氏時空)中，時空的性質由洛倫茲變換來反映.由洛倫茲變換能給出伽利略變換嗎？所需要的條件又是什么呢？文獻[2]認為，僅僅要求低速條件是不充分的.本文將就這一問題進行一些討論.

1 洛倫茲變換的低速近似

1.1 洛倫茲變換

狹義相對論的兩個基本原理是該理論的物理基礎和核心內容.相對性原理自身是物理規律表述的一個要求.對于任何一個關于自然科學的理論，都有規律表示不變性的要求，否則就不能很好地描述自然.由狹義相對論中的兩個基本原理，可導出兩個慣性系之間的坐標變換—洛倫茲變換.

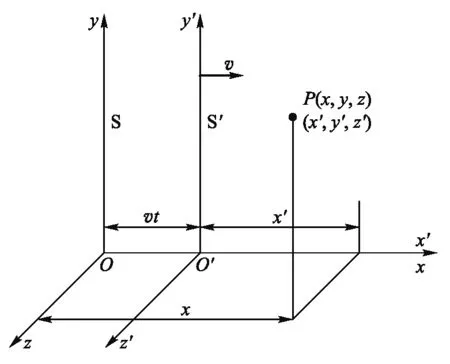
圖1 相對運動的兩慣性系

假定兩個參考系S′和S的3個空間坐標軸取向都相同，且S′系相對S以不變速度v沿x軸的正方向運動，則洛倫茲變換為[3]

(1)

在y和z兩個空間方向上，新坐標取相同值或相差一個常數.上式也可稱為1+1維閔氏時空的坐標變換.

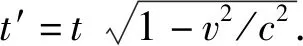
一般情況下，式 (1)中的空間坐標x是時間t的函數，x=x(t)，對于這個函數形式沒有特殊要求.當x=x(t)滿足線性關系時，變換(1)會線性地依賴時間t.該情況下，容易導出兩個慣性系間的速度變換式.

1.2 洛倫茲變換的低速近似

一般地認為，在低速條件v<

(2)

忽略掉v/c的三級小量后，上式化為

(3)

我們稱式(3)為洛倫茲變換(1)的低速近似.

通常情況下，在對洛倫茲變換進行近似處理的過程中，只考慮了涉及到速度比率v/c的因素.實際上，還有一個因素也需要考慮，就是x與vt的關系，它涉及到是否可以忽略掉式(3)下式中的vx/c項的問題.

在x<

顯然，存在第三種情況x?vt.該情況下，忽略v/c的二級小量后，式(3)可近一步化為

(4)

為了近似地給出伽利略變換，需要近一步給出關于空間坐標的限制條件：

(5)

上式不同于文獻[2]給出的條件x<

2 討論

在低速情況下，一般可認為洛倫茲變換近似化為伽利略變換.其實不然，伽利略變換丟掉了反映時空結構性質的重要信息，只能說伽利略變換近似適用于低速情況.作為反映物理時空性質的變換，伽利略變換是經驗性的.只有對伽利略變換進行適當修改，才可以作為低速條件下洛倫茲變換的近似形式.