Exact solutions of three classes of conformable time-fractional differential equations

Wang Xiaoli,Cheng Xiaoyu,Wang Lizhen,Yang Miao

(School of Mathematics,Northwest University,Xi′an 710127,China)

Abstract：The aim of this paper is to construct the exact solutions of three classes of time-fractional differential equations with conformable derivative such as Airy′s equation and Telegraph equation by means of the functional variable separation method and generalized variable separation method.For the conformable fractional inviscid Burgers equation,we study its exact solutions using the generalized variable separation method.The results obtained shows that this method is direct and concise.In addition,we also present the three-dimensional diagrams of some exact solutions with the help of Maple.

Keywords：conformable fractional equations,functional separated variable solution,generalized variable separation method

1 Introduction

The idea of fractional derivative has been proposed by L′Hospital in 1695.Since last century,people have made deep development on fractional calculus and many de finitions of fractional derivative have been introduced.The most two popular definitions are Riemann-Liouville derivative and Caputo derivative.

Definition 1.1(Riemann-Liouville derivative)Ifn∈Z+andα∈[n?1,n),thenα-th order derivative offin Riemann-Liouville derivative sense is defined by

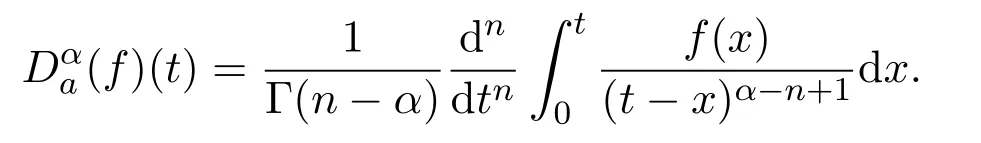
Definition 1.2(Caputo derivative)Forα∈[n?1,n),the Caputo derivative withα-th order offis defined by

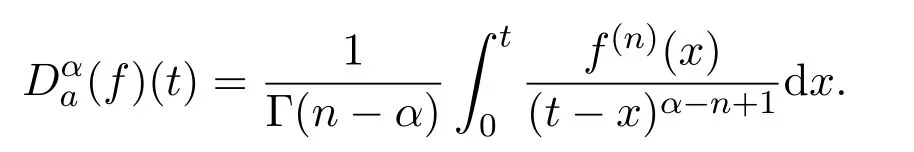
Recently,Reference[1]introduced a new definition of fractional derivative and fractional integral.And Reference[2]studied the Taylor power series representation and Laplace transform of few certain functions,chain rule and fractional integration by parts formulas.The exact solutions of the time-fractional differential equations were constructed by using various methods such as Lie symmetry analysis[3-9],the first integral method[10-12],separating variables method[13-15],q-homotopy analysis transform method[16-17]and invariant subspace method[18-24],and so on.

In this paper,we utilize separation variables methods to construct the exact solutions of the following three equations.The first one is conformable time-fractional Airy′s equation

The second one is conformable time-fractional Telegraph equation

The last equation is conformable time-fractional inviscid Burgers equation

whereu(x,t)is a real-valued function.d>0 is a constant andα∈(0,1].Tαdenotes the conformable fractional derivative and

2 Preliminaries

Definition 2.1[1](Conformable fractional derivative)Letα∈(0,1]and fort>0,f:[0,∞)→R.The conformable fractional derivative of functionf(t)with orderαis defined by

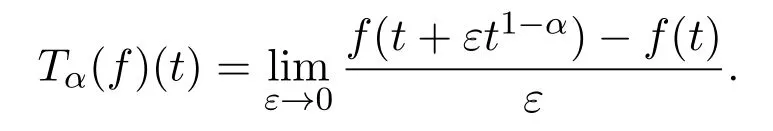
In addition,if functionf(t)has the conformable fractional derivative with orderαin(0,∞),we call thatf(t)isα-differentiable in(0,∞).And iff(t)isα-differentiable in interval(0,∞)andexists,then we define

Denotef′(s)to be the first order derivative off(s)with respect to independent variables.Then the following properties are held to be true.

Lemma 2.1[1-2]Letα∈(0,1]and fort>0,then

(i)Tα(f)(t)=t1?αf′(t),iffis differentiable.

(ii)Tα(fg)(t)=g(t)Tα(f)(t)+f(t)Tα(g)(t),wheref,gareα-differentiable.

(iii)Leth(t)=f(g(t)),fbe differentiable andgbeα-differentiable.Thenh(t)isα-differentiable andTα(h)(t)=f′(g)(t)Tα(g)(t).

Next,we provide the details of the methods of separation of variables introduced in Reference[25].

Step 1:Consider the following general conformable differential equation

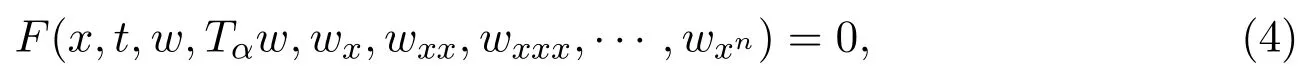
wherewxnmeans then-th order derivative of functionw(x,t)with respect tox.

Step 2:Searching for the generalized separable solutions with the form as follows

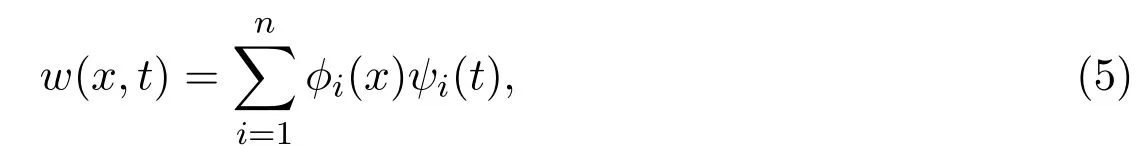
where?i(x)andψi(t)are smooth enough.Substituting(5)into original equation(4),we can write out the following functional differential equation

and get the solution Φi(t)and Ψi(x)(i=1,2,···,n)of(6)to obtain the determining system.

Step 3:Solving the fractional determining system to find the exact formulas ofψi(x)and?i(t)and inserting them into(5)to obtain the presentation of the exact solutionw(x,t).

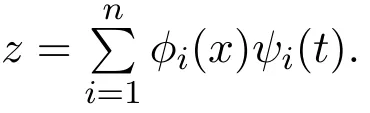
3 Solutions to conformable time-fractional Airy′s equation

In this section,we intend to establish the exact solutions of conformable fractional Airy′s equation applying functional variable separation method and generalized variable separation method.

Case 3.1The application of functional variable separation method.

Assume that the solution of equation(1)has the following form

whereF(z)andψ(t)0 are the unknown functions which will be determined later.Insert(7)into(1)to obtain the following functional differential equation

whereCi(i=1,···,4)are arbitrary constants andmis a nonzero constant.Combining equations(10)-(11)with equation(12),we get the following two traveling wave solutions of equation(1)

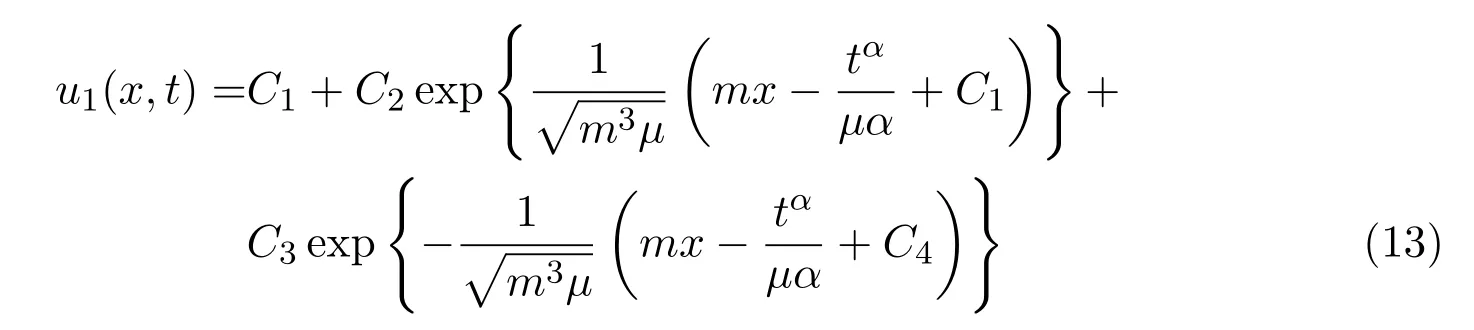
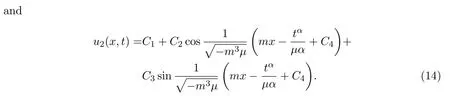
With the help of Maple software,if we takeC1=m=1,C2=2,C3=3,C4=0,μ=?1,α=0.9 in(14),we can derive the 3D plot ofu2(x,t).

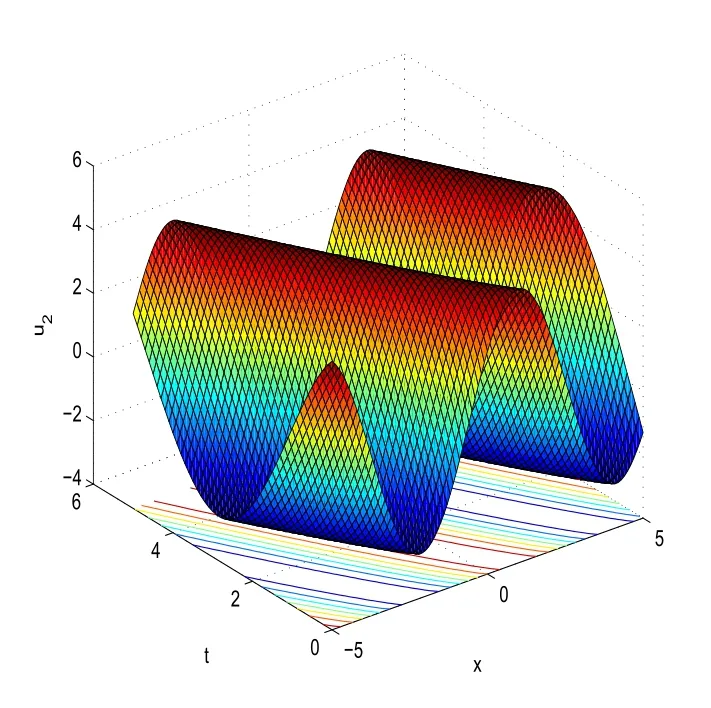
Fig.1 3D plot of u2(x,t)obtained in(14)

Case 3.2The application of generalized variable separation method.

(1)Assuming that

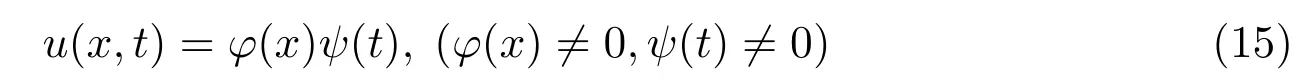
and substituting equation(15)into equation(1),we obtain

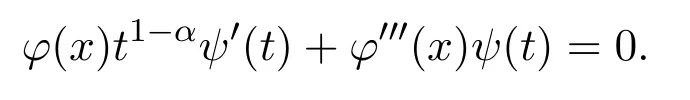
For some constantμ,we have

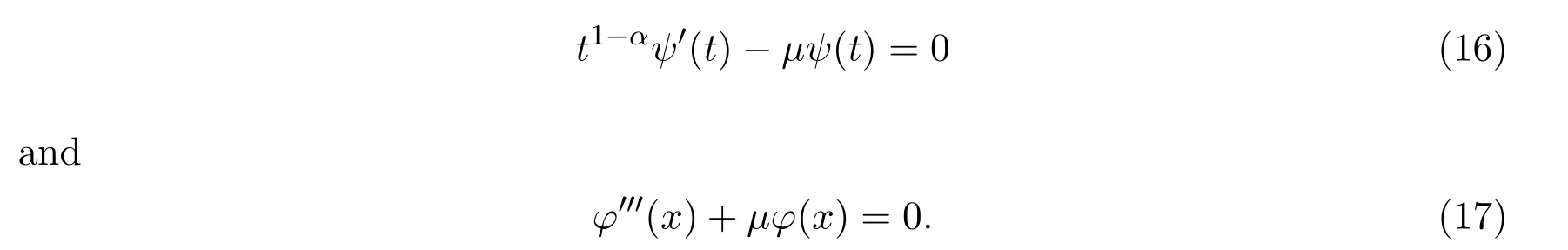
Solving equations(16)and(17),we have

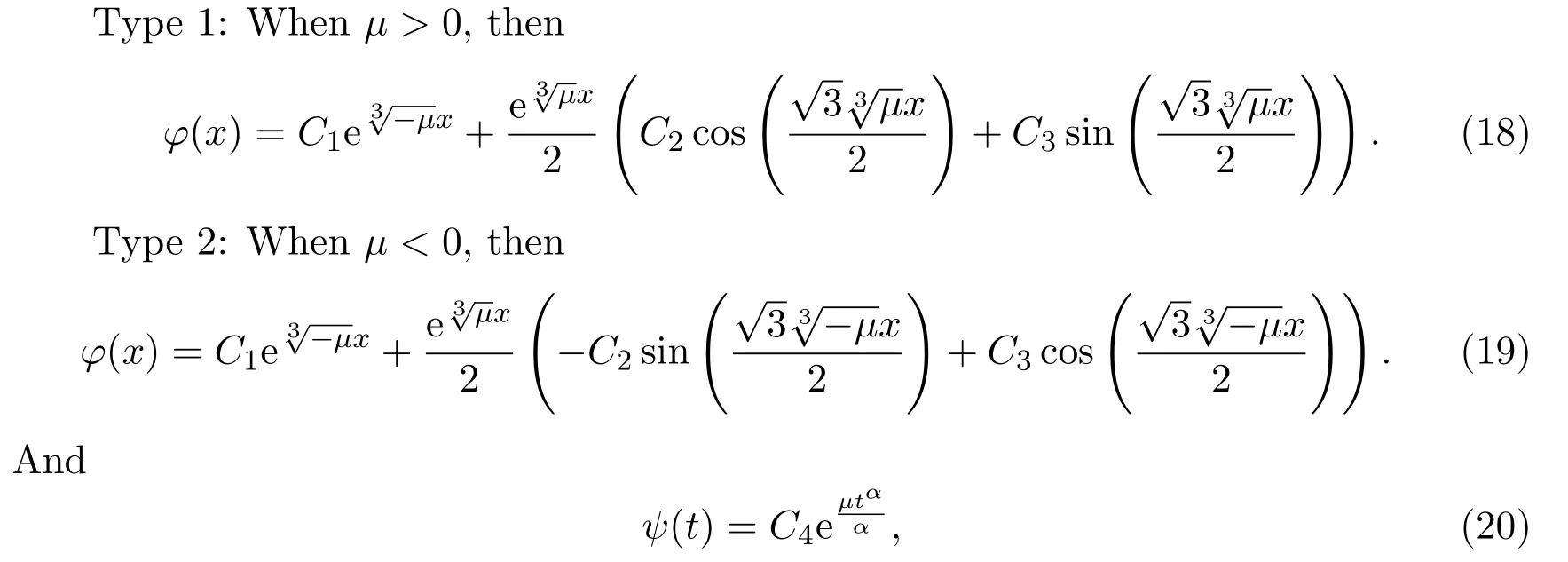
whereCi(i=1,···,3)are arbitrary constants andC4is a nonzero constant.In conclusion,combining equations(18)-(20)with equation(15),we get the exact solutions of equation(1)with the following form

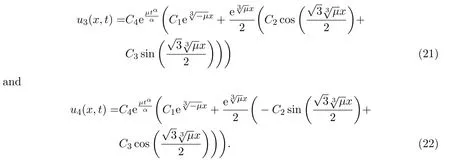
With the help of Maple software,if we takeC1=C4=1,C2=2,C3=3,μ=1,α=0.1 in(21),we can derive the 3D plot ofu3(x,t).And if we takeC1=C4=1,C2=2,C3=3,μ=?1,α=0.7,we can obtain the 3D plots ofu4(x,t)

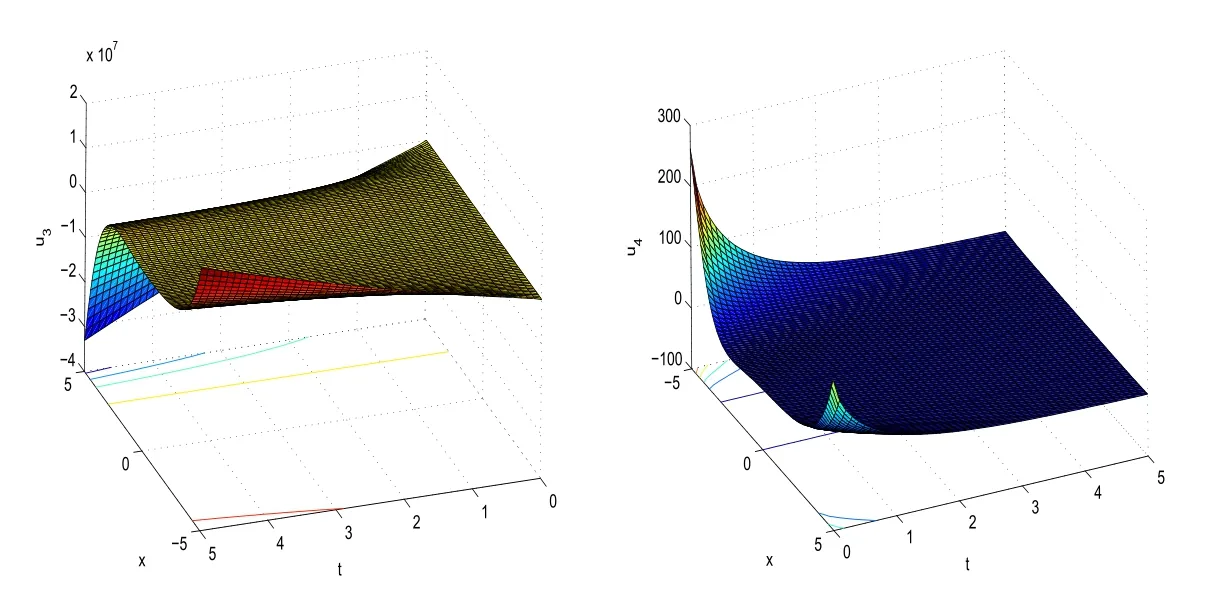
Fig.2 3D plot of u3(x,t)obtained in(21)and u4(x,t)obtained in(22)

(2)Supposing that

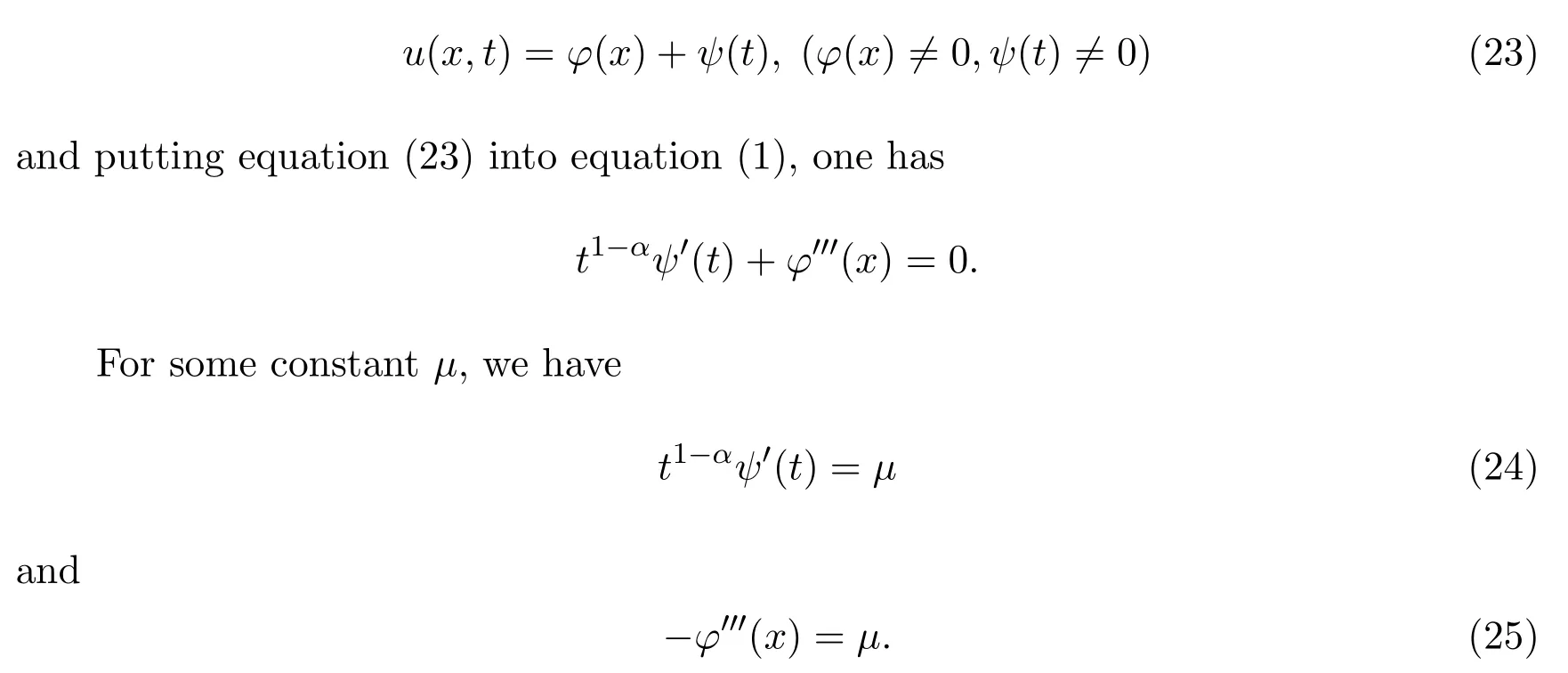
Solving equations(24)and(25),we get

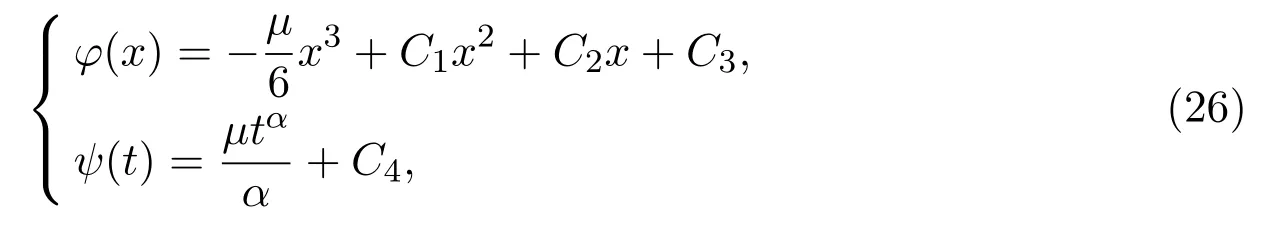
whereCi(i=1,···,4)are arbitrary constants.With the help of equation(26)and equation(23),we get the exact solution of equation(1)with the following form

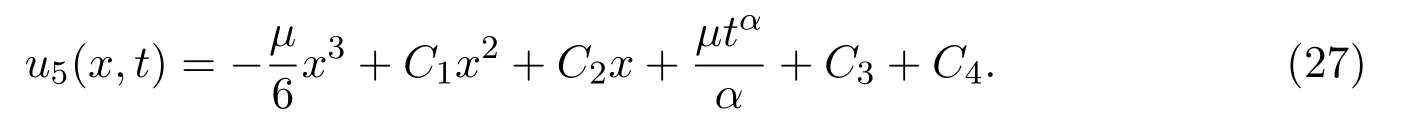
With the help of Maple software,if we takeC1=1,C2=2,C3=C4=0,μ=5,α=0.9 in(27),we can derive the 3D plot ofu5(x,t).

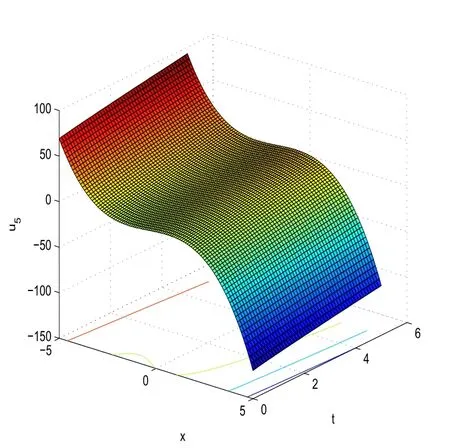
Fig.3 3D plot of u5(x,t)obtained in(27)

4 Solutions to conformable time-fractional Telegraph equation

In this section,we intend to establish the exact solutions of conformable fractional Telegraph equation applying functional variable separation method and generalized variable separation method.

Case 4.1The application of functional variable separation method.

Assume that the solution of equation(2)has the following form

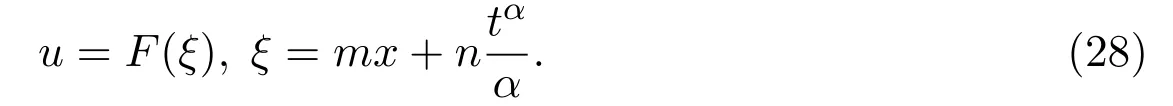
Insert(28)into(2)to obtain the following functional differential equation

Combining equation(28)with equation(29),the traveling wave solution of conformable time-fractional Telegraph equation is obtained in the form

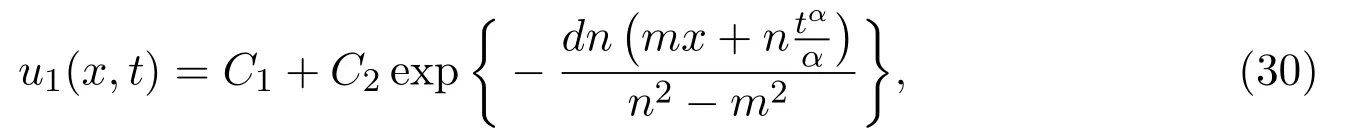
whereC1andC2are arbitrary constants.

Case 4.2The application of generalized variable separation method.

(1)Assuming that

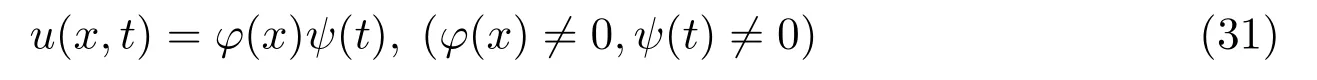
and inserting equation(31)into equation(2),one has

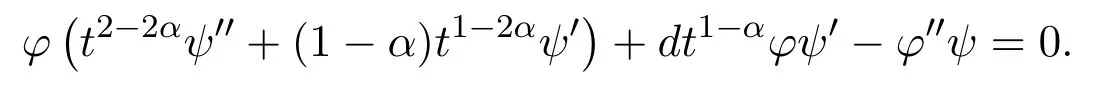
For some constantμ,we have

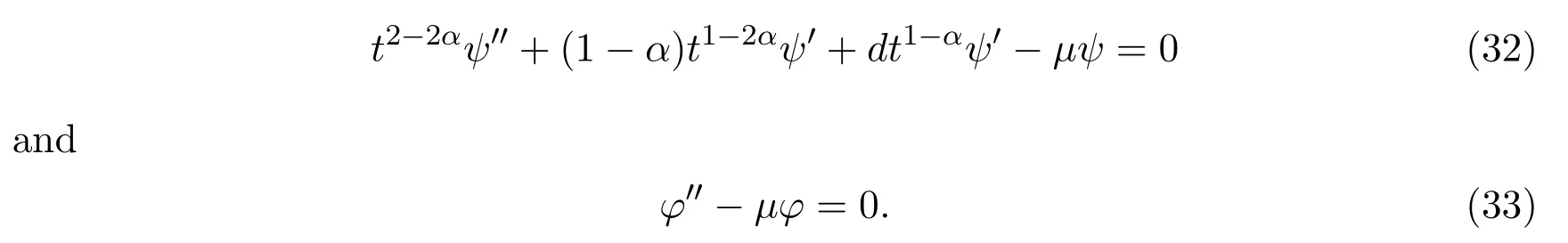
Solving equations(32)and(33),one has

Type 1:Whenμ>0,then for arbitrary constantsCi(i=1,···,4),we have

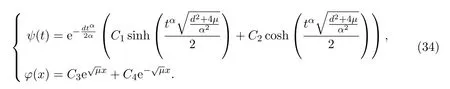
Type 2:Whenμ<0,then for arbitrary constantsCi(i=1,···,4),we have

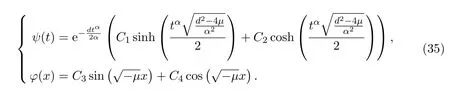
Type 3:Whenμ=0,then for arbitrary constantsCi(i=1,···,4),we have

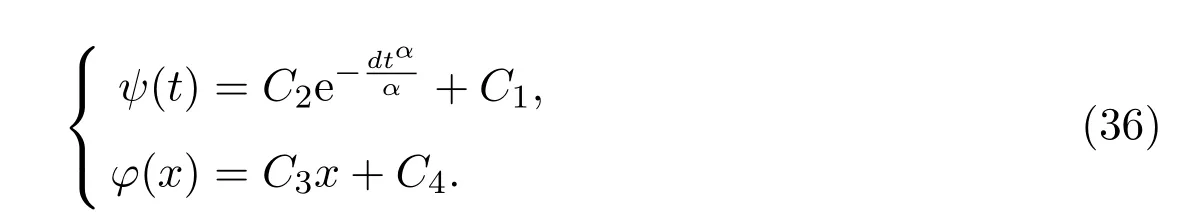
Combining equation(31)with equations(34)-(36),solutions of conformable timefractional Telegraph equation are written as bellow

With the help of Maple software,if we takeC1=d=1,C2=μ=2,C3=3,C4=4,α=0.9 in(37)and(38),we can derive the 3D plot ofu2(x,t)andu3(x,t).

Fig.4 3D plots of u2(x,t)obtained in(37)and u3(x,t)obtained in(38)

(2)Supposing that

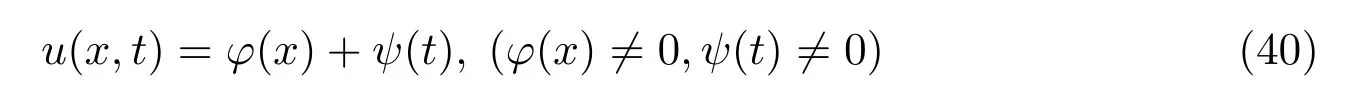
and substituting equation(40)into equation(2),we get

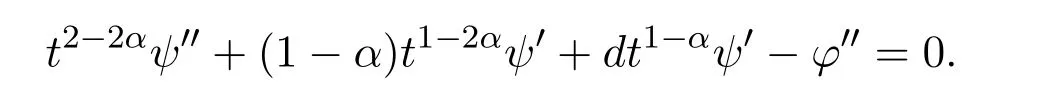
For some constantμ,one has

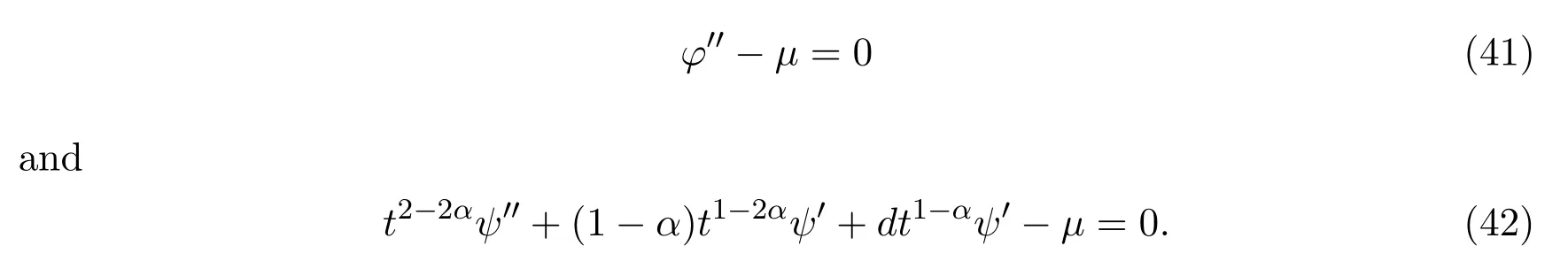
Solving equations(41)-(42),we have

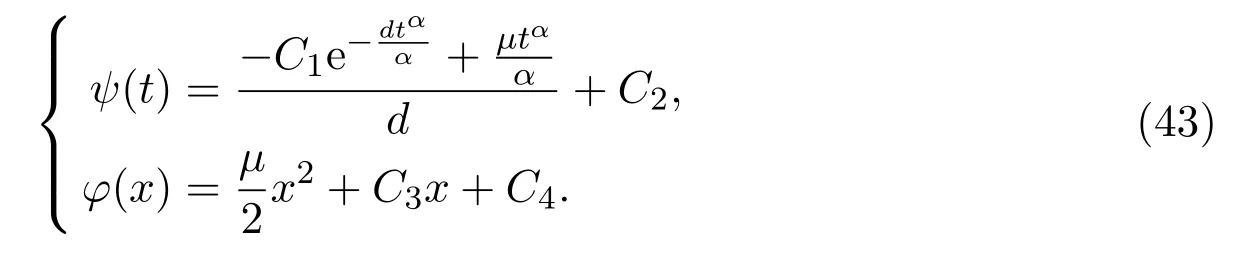
Combining(40)with(43),solution of conformable time-fractional Telegraph equation is written as bellow

With the help of Maple software,if we takeC1=1,C2=2,C4=4,d=3,μ=?1,α=0.5 in(44),we can derive the 3D plot ofu2(x,t)andu5(x,t).

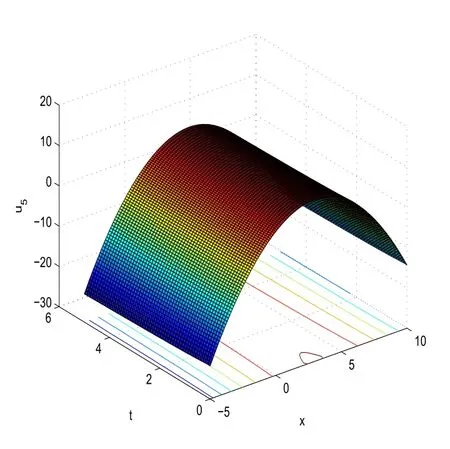
Fig.5 3D plot of u5(x,t)obtained in(44)

5 Solutions of the inviscid Burgers equation

In this section,we intend to establish the exact solutions of conformable fractional inviscid Burgers equation applying generalized variable separation method.

Case 5.1Assumeu(x,t)=φ(x)ψ(t).Substitute it into equation(3),one has

Separate the variables in(45)and solve them to find that

whereμis a nonzero constant andC1,C2are arbitrary constants.Putting(46)into the expressionu(x,t)=φ(x)ψ(t),we obtain the solution to equation(3)as follows

With the help of Maple software,if we take

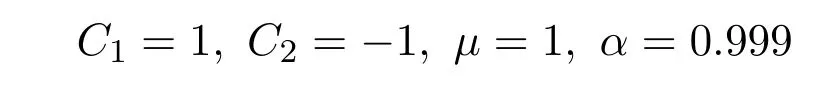
in(47),we can derive the 3D plot ofu1(x,t).

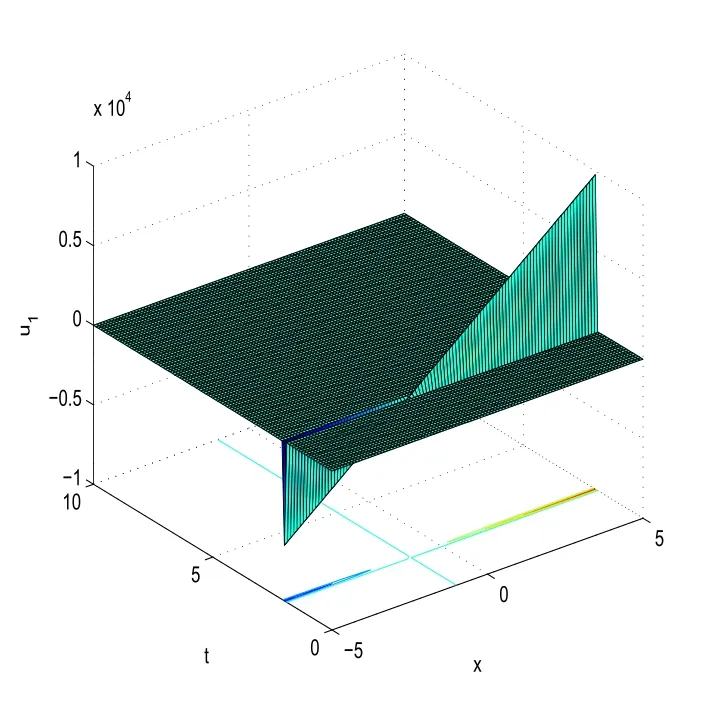
Fig.6 3D plot of u1(x,t)obtained in(47)

Case 5.2We seek an exact solution with the following form

Substituting(48)into equation(3)to get the following functional equation

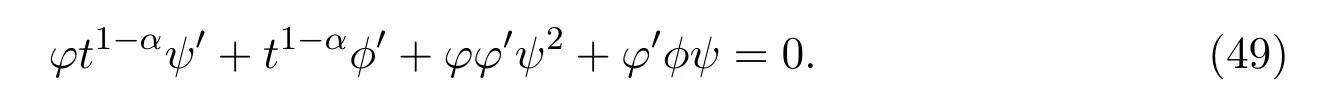
Rewrite(49)as the following bilinear form

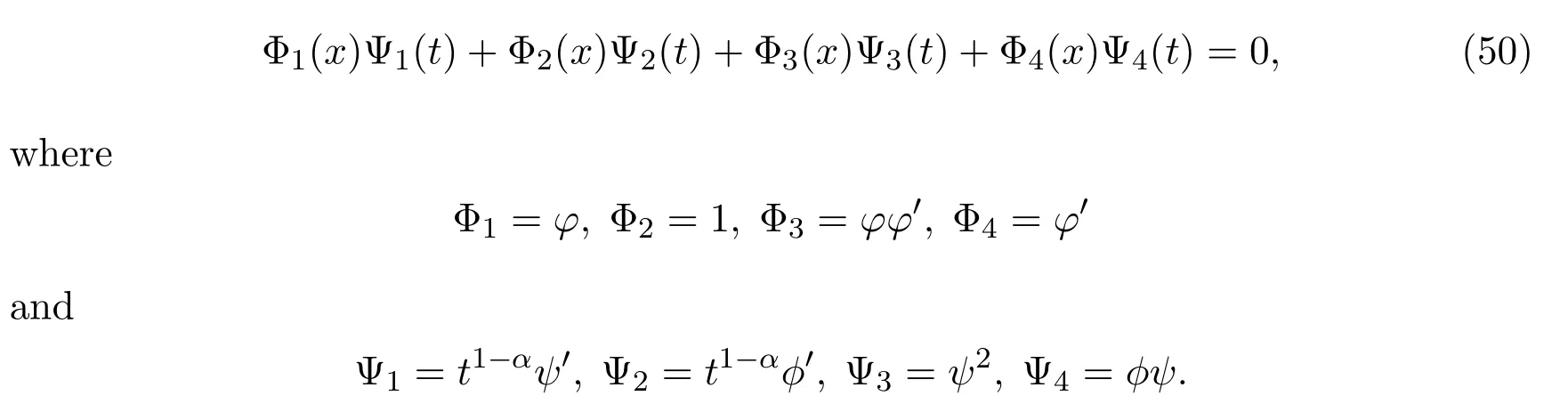
Using the solution formula of functional differential equations of splitting method introduced in Reference[25],one has

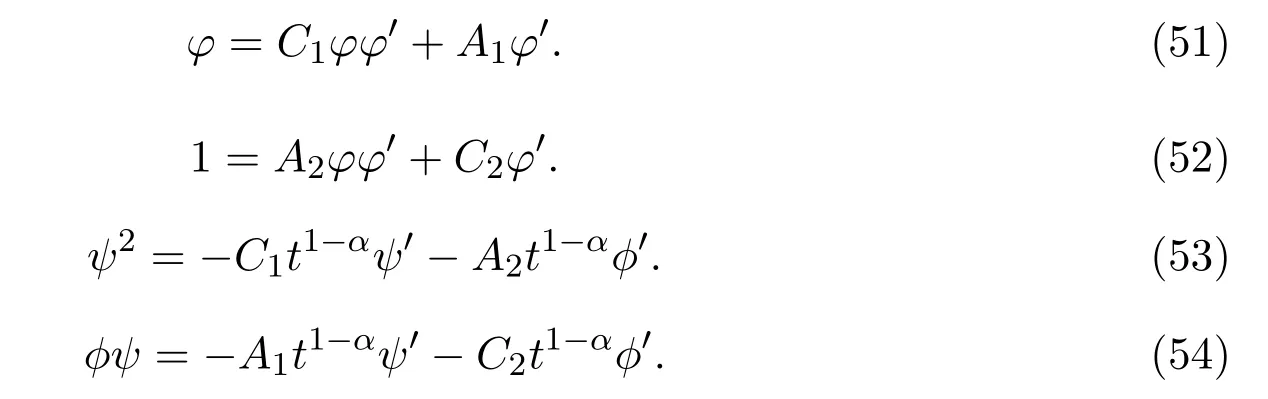
LetA1=A2=0,C1=C2=1 and solve(52)to yield

Furthermore,one has

Solve(56)and(57)to obtain

whereAi(i=1,2,···,5)are arbitrary constants.Putting equations(55),(58)and(59)into equation(48),we obtain the exact solution for equation(3)

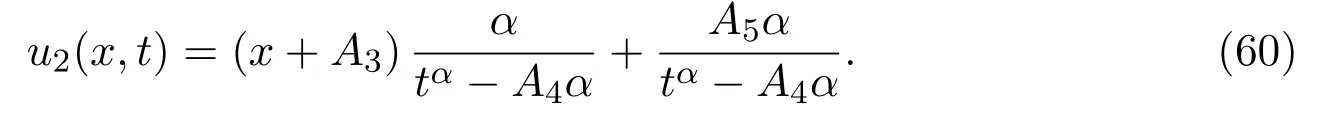
With the help of Maple software,if we takeC1=1,C2=2,A3=3,A4=4,A5=5 andα=0.5 in(60),we can derive the 3D plot ofu2(x,t).

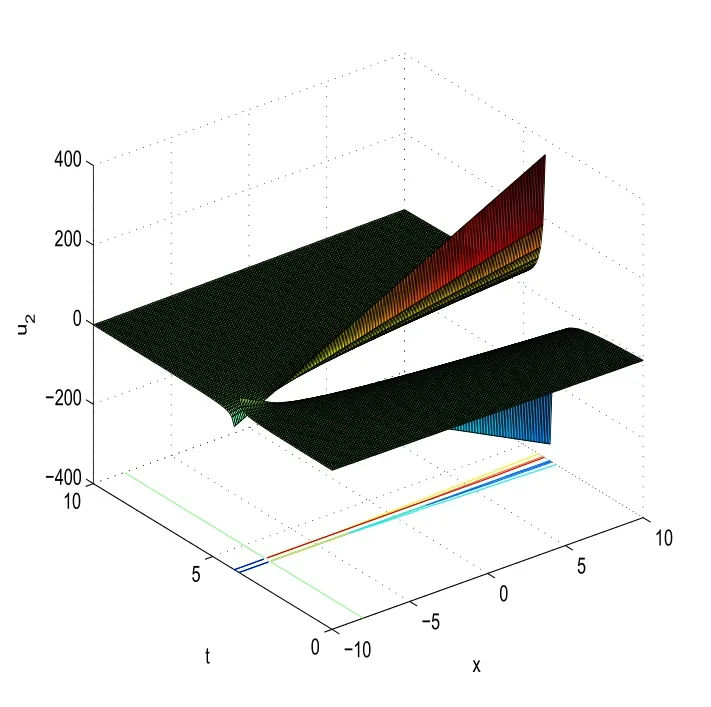
Fig.7 3D plot of u2(x,t)obtained in(60)

6 Conclusion

In conclusion,we obtain the exact solutions for Airy′s equation,Telegraph equation and inviscid Burgers equation in the sense of conformable fractional derivative successfully by using the separating variables method.Moreover,we obtain some traveling wave solutions which have important physical significance.we select some solutions and present their three-dimensional images with the help of Maple.Additionally,we observe that this method is direct and concise.It is an effective method and can be extended to solve conformable fractional partial differential equations.