小學數學教學中如何引導學生積累數學活動經驗

儲劉純

小學數學教學不僅要讓學生掌握基礎知識和基本技能，還要引導學生在自主學習過程中進行數學活動經驗積累，這樣才能為促進他們的數學核心素養奠定基礎。數學活動經驗是看不見、摸不著的，需要教師在課中點滴滲透，在傳授知識的同時，關注學生經驗積累。以“平行四邊形的面積”為例，淺談小學數學教學中如何引導學生積累數學經驗，以促進他們數學核心素養的提升。

一、引發思維碰撞，暴露原有經驗

要上好一節課，首先需要知道老師解決的問題是什么？或是學生的困惑在哪里？只有找準這些，學習才能真正發生。如何準確發現學生的困惑呢？在課堂上讓學生展現或暴露原有的經驗十分重要。

問題情境：用木條做一個長7cm、寬5cm的長方形邊框，其面積是多少？如果把它拉成平行四邊形，其周長和面積有沒有變化？

學生的分歧為：有的認為面積不變，有的認為面積變了。學生思維的分歧暴露了學生原有的一些經驗。

觀點一：因長方形的面積是長乘以寬，所以，很多學生認為平行四邊形的面積也是相鄰兩條邊相乘，面積沒有變。

觀點二：有學生認為長方形的周長沒變，只是形狀變了，平行四邊形的面積也應該不變。

觀點三：也有學生理性地通過底和高的分析，推算出面積變小了。

這個活動讓學生暴露了面積計算的一些經驗。首先，學生會把這樣的經驗遷移到計算平行四邊形面積中去;其次，學生對面積變化的判斷，還會受到周長的干擾;第三，部分學生已學過公式，但為什么這樣做不清楚。基于這些情況，將研究目標設為“在周長不變的情況下面積到底變不變”的問題。解決了這個問題，其實就幫學生重新積累新的經驗。可見，教師應精心設計教學環節，幫助學生暴露原有的經驗，以原有經驗為生長點展開教學，使學生獲得新經驗。

二、設計探究任務，引發經驗生成

當確定問題后，讓學生利用原有經驗，通過探究生成新的經驗，再利用新經驗嘗試解決問題。

1.研究問題：相鄰的兩邊仍是5 cm和7 cm，這個平行四邊形的面積是不是35（cm2）？如果不是，那應是多少？

2.研究方法：數一數，畫一畫，剪一剪。

3.研究材料：格子圖一份、一個平行四邊形（選其一）

4.研究流程：獨立研究，算出長方形面積→同桌交流，說說各自計算方法→匯報小結。

這一過程，學生就生成了新的經驗，把未知的轉化成已知的，其轉化的過程就是問題解決的過程。所以課堂探究任務設計要回歸學生經驗，且要利用這些經驗去解決新的問題。

三、組織討論交流，促進經驗積累

學生在活動中獲得的新經驗，往往是比較零散、模糊的，這就需要教師適時引導，讓學生把新經驗進行分析、整理，進而清晰、全面。

1.以問引思：你是怎么轉化的？面積是多少？你能推導出平行四邊形面積公式嗎？

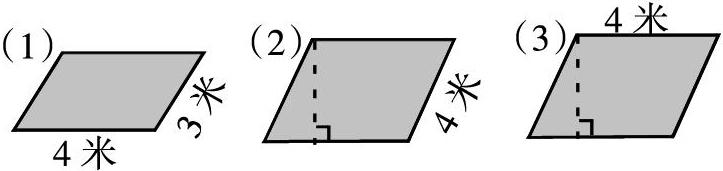
2.對比分析：下面哪個圖形的面積可以用3×4=12平方米來計算面積？

3.變式訓練：計算下面圖形的面積，哪個算式是正確的？

這一環節，先讓學生說說怎么轉化的，大部分學生的方法就是沿著頂點畫下來的高剪開，變成一個平行四邊形。通過學生討論，結合課件動態演示，讓學生獲得新經驗。那就是還可以沿著中間的高剪，也可沿著上下底邊上的高、左右鄰邊上的高剪都行。

整個實踐過程老師發現，學生雖經歷了，但沒有積累相應的經驗，這是為什么呢？通過多次實踐，老師發現經驗積累的“一些方法”。

原來反饋設計：學生獨立研究→小組討論交流→小組匯報公式推導過程。

現在反饋設計：學生獨立研究→小組討論交流→討論轉化過程→討論面積公式推導過程。

實踐表明，第二種反饋學生在說推導過程時，說得更具體、更準確，且大部分學生都能說出面積公式的由來。而第一種反饋，只有部分成績好的學生能夠推導出面積公式，相當一部分學生束手無策。

這節課例讓我充分認識到，在“四基”目標下，小學數學教學關注學生的經驗積累十分重要。