基于模型跟蹤變結構算法的電子節氣門控制

賈東明，張昊

（1.河南交通職業技術學院汽車學院，河南鄭州450000；2.東南大學儀器科學與工程學院，江蘇南京210000）

近年來，世界各國的汽車產銷數量都在不斷增長，日益增加的汽車產生的尾氣排放問題對全球環境造成了極大壓力。最早，節氣門在汽車上的使用是采用機械連接的，也就是通過拉索將節氣門和油門踏板連在了一起，當駕駛員踩下油門踏板時拉索便拉動節氣門閥板打開，當駕駛員放開油門踏板時，在彈簧的回力作用下，節氣門閥板關閉。這種聯動方式簡單直接卻不利于精確控制，因此對汽車油耗的降低形成了桎梏。并且汽車只能被動地測量進氣量來進行內燃機的轉速控制，而不能通過節氣門或者油門踏板的位置來主動參與控制，所以對行駛安全性也造成了一定影響。為了解決這一問題，伴隨著電子技術的不斷進步，國外的汽車零部件制造機構逐步將電子節氣門應用到汽車上。電子節氣門控制系統由油門踏板、電子節氣門本體、電子控制單元（electronic control unit，ECU）等組成。駕駛員踩踏油門踏板時，并不會直接驅動節氣門，而是先將踏板信息進行采集，輸入到控制單元中，控制單元根據輸入信息及預存在其中的控制算法來驅動節氣門閥板打開并進行開度的精確控制。例如，當內燃機啟動時，即使駕駛員還沒有踩踏油門踏板，但出于怠速要求，節氣門閥板必須已經打開一定角度從而保證初始進氣量。這樣，系統完全可以根據駕駛員意圖以及內燃機實際工作情況來綜合判斷節氣門電機的打開程度，而不是進行單一的跟蹤式控制。

節氣門閥板開閉的控制與汽車的排放控制是息息相關的。節氣門一方面作為汽車發動機控制系統的關鍵部件，一方面又對內燃機的進氣量及空燃比形成了影響。因此，節氣門的控制精確程度影響到了進氣系統控制、空燃比控制、廢氣再循環控制等，并最終對排放的控制形成了影響[1-2]。

PID控制作為控制領域應用最為廣泛的控制算法，自然而然地被應用于電子節氣門的控制，并成為了目前電子節氣門控制中使用最多的算法。如果被控系統能夠被準確建立數學模型，或者即使無法準確建模但系統不存在參數漂變，那使用PID算法也都是能夠精確控制的。但對于電子節氣門而言，很難準確建模，即使模型建立也可能會隨著使用時間的增加而導致模型參數漂變，并且節氣門在整個工作過程中難免會受到氣流影響而產生擾動。從這些角度來講，初期能夠勝任控制精度要求的PID算法，其控制精度必然會隨著汽車使用時間的增長而逐漸下降[3]。

近年來，眾多國內外學者對電子節氣門的控制算法進行了研究。有的針對PID算法進行了優化[3]，有的直接使用智能化算法進行控制[4-8]。本文針對電子節氣門會隨著時間推移而發生參數漂變、難以建立準確數學模型以及工作過程中存在各種擾動的情況，提出模型跟蹤變結構算法，并與模型參考自適應算法的控制結果進行對比，得出了新算法響應速度快、魯棒性強的特點。從而解決了建模不準、參數漂變、動態擾動所帶來的種種問題。

1 電子節氣門數學模型的建立

電子節氣門數學模型的建立主要包括電機、復位彈簧、齒輪減速機構、閥片摩擦力矩等模型的建立。

1.1 電機模型

驅動電機數學模型的建立主要依據基爾霍夫電壓定律進行確定：

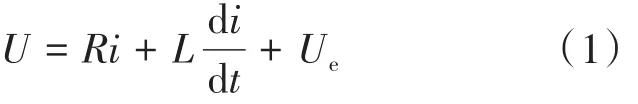
式中：R為電機的等效電阻；i為電機電樞通過的電流；L為線圈的等效電感；U為電機輸入的電壓；Ue為電機反向電壓。

實際在電機的眾多參數中電感數值比較小，通常可以忽略不計，所以式（1）可以簡化為

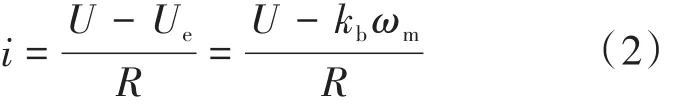
式中：kb為電機所產生的反向電動勢常數；ωm為電機旋轉的角速度。

從而可以得到電機轉矩方程如下：

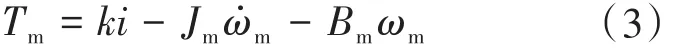
式中：k為電機的轉矩系數；Bm為電機的阻尼系數；Jm為電機主軸的轉動慣量；ω?m為電機旋轉時的角加速度。

1.2 復位彈簧模型

為了使電子節氣門在初始的時候能夠有一定的開度，所以在其中使用了兩個彈簧，分別是開啟彈簧和回位彈簧。當電子節氣門閥板的轉角θ大于初始位置轉角θ0時，只有返回彈簧提供力矩來保證閥板返回θ0；當閥板轉角θ小于初始位置轉角θ0時，開啟彈簧和回位彈簧同時提供相反方向的力矩，這時彈簧組的輸出力矩就是兩個彈簧的力矩之差。節氣門所受的轉矩為

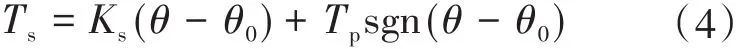
式中：Ks為復位彈簧彈性系數；Tp為復位彈簧預緊力矩。

1.3 齒輪減速機構模型

電子節氣門驅動電機輸出為高轉速低轉矩，可以通過一組相互嚙合的齒輪將動力轉換為低轉速高轉矩。減速齒輪的傳動比為

式中：ωt為電子節氣門閥板轉動的角速度。

1.4 摩擦力矩數學模型

電子節氣門體中的摩擦力矩主要來源于黏性摩擦力矩Td和庫侖摩擦力矩Tf。總摩擦力矩Tr就是這兩種摩擦力矩之和，即

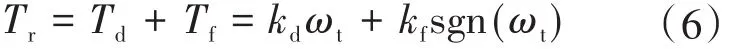
式中：kd為黏性摩擦系數；kf為庫倫摩擦系數。

1.5 節氣門執行機構的數學模型

電子節氣門閥板是受到多個力矩的共同作用而進行運動的，主要包括以下三個力矩的作用：由直流電機所提供的驅動力矩Tm是最主要的力矩，由復位彈簧產生的彈簧力矩Ts以及節氣門閥板在運動過程中所受到的總摩擦力矩Tr也參與其中。通過上述分析，可得出電子節氣門執行器的動力學方程如下：

式中：Jt為節氣門閥板軸的轉動慣量；ω?t為節氣門閥板運動時的角加速度。

將式（3）～式（6）代入式（7）并進一步化簡得到：

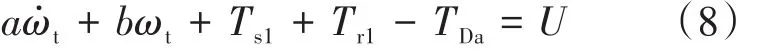
其中

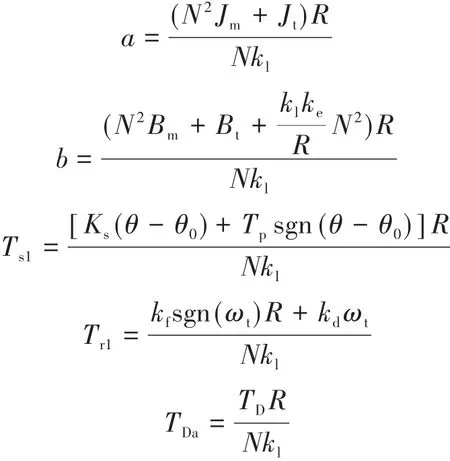
式中：kl為電機的轉矩系數；ke為電機反向電動常數；Bt為節氣門黏性阻尼系數；TD為系統內部干擾。

如果以節氣門轉動的角度θ作為變量，則可以得到一個二階系統，其傳遞函數如下：

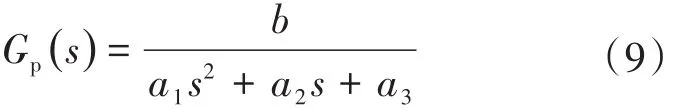
可將其轉化成能控能觀的狀態方程如下：

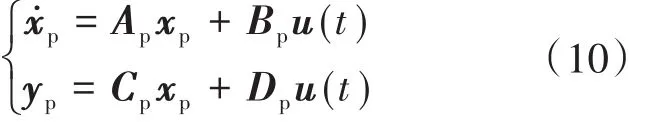
代入具體數據之后可得：

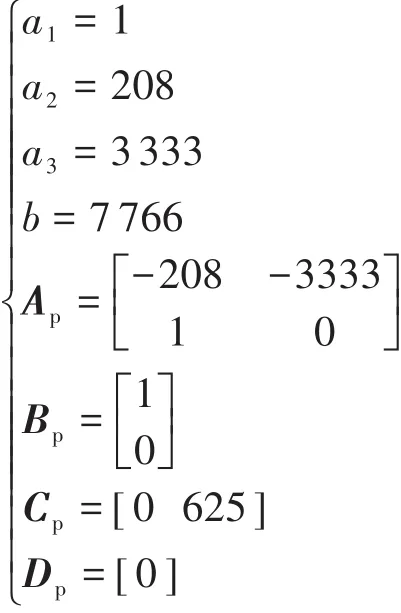
2 目標模型的確定

為了使得電子節氣門的控制性能可以滿足要求，我們可以設定一個目標模型進行參考。如果最終控制的結果能夠擬合所設定模型的控制過程，則節氣門的控制結果也是令人滿意的。通常為了滿足擬合過程，所使用的算法是模型參考自適應算法，它將參考模型Gm（s）放至外環，可調節參數的算法與被控模型Gp（s）放至內環，以二者的輸出差作為評判，致力于使得被控模型最終與參考模型相匹配。本文的目的是追蹤參考模型的輸出，而不糾結模型是否匹配。但無論是進行模型匹配還是進行模型跟蹤，都需要有一個滿足性能的模型。

由電子節氣門的數學模型我們可以得知，現需要建立一個二階系統的模型，且模型的各種性能均能符合我們的要求。

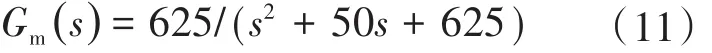
設定參考模型如下：轉換成狀態方程如下：

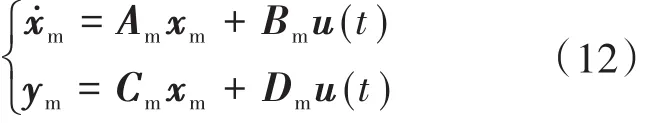
其中

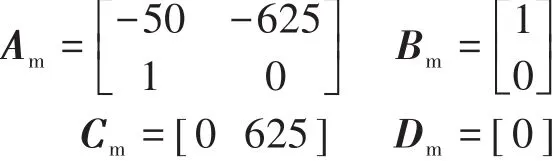
理想模型的正弦跟蹤曲線及單位階躍響應曲線如圖1、圖2所示。

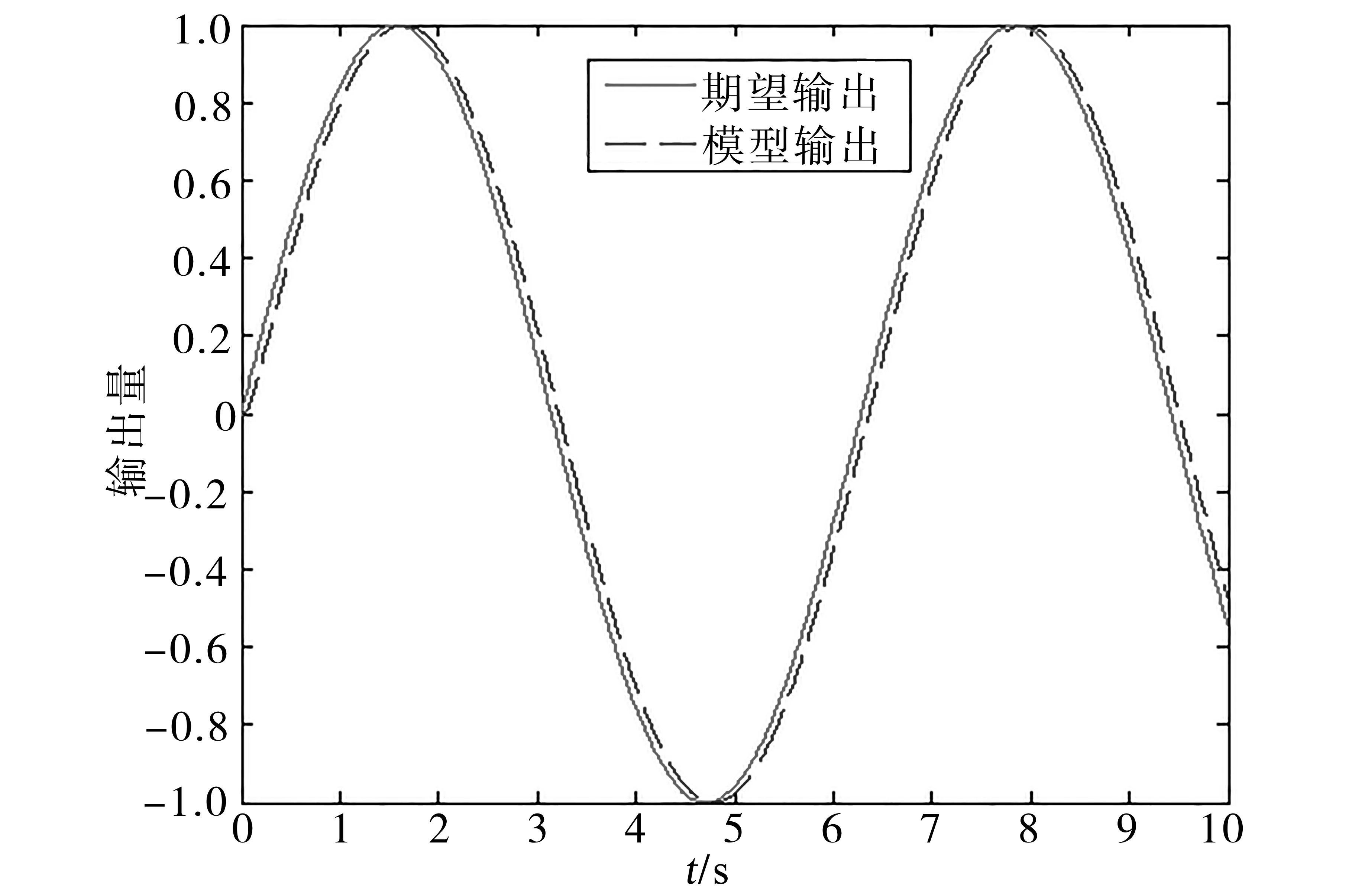
圖1 理想模型的正弦跟蹤曲線Fig.1 Sine tracing curves of ideal model

通過圖1和圖2可以看出，模型對正弦曲線的跟蹤存在一定的滯后，但數值很小。模型對單位階躍信號的響應曲線沒有超調量，且0.3 s左右即跟蹤上期望輸出。因此所設定的參考模型能夠滿足需求。

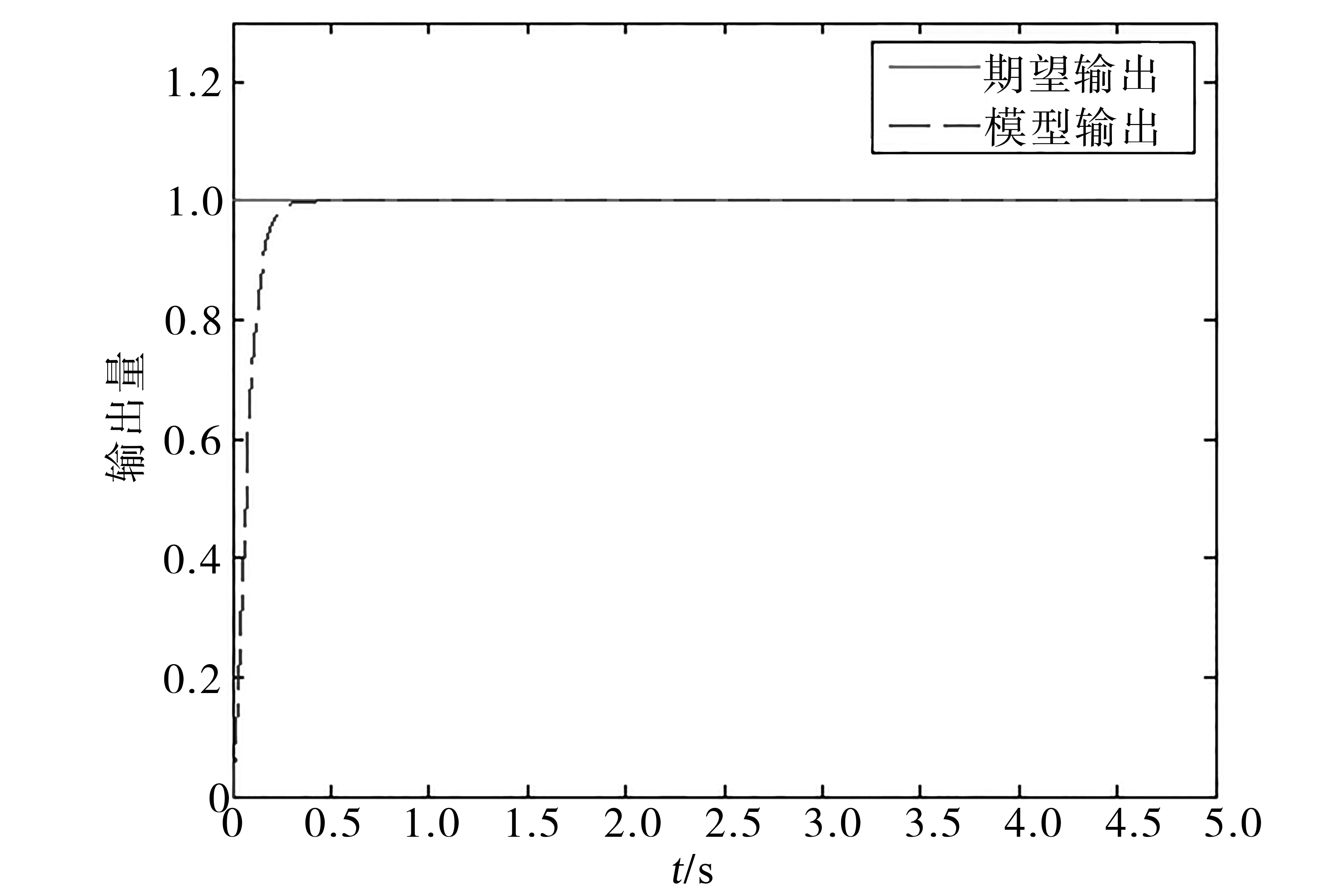
圖2 理想模型的單位階躍響應曲線Fig.2 Unit step response curves of ideal model

3 模型參考自適應控制

模型參考自適應控制是進行模型匹配的有效算法。最早由麻省理工學院所提出的MIT控制律是基于局部參數最優化的方法。該方法比較直觀并便于理解，但是卻無法保證閉環系統的穩定性，從而使得其應用受到了限制。20世紀60年代中期由Butcharty和Parks相繼提出的基于Lyapunov穩定理論的模型參考自適應控制，不僅使得系統穩定性得到了保障，而且相較于MIT自適應具有更快的控制速度。其控制的目的是使被控系統經調節后與模型趨于一致，從而最終實現參考模型輸出的跟蹤。

自適應控制在被控系統上加入可調節的前饋控制參數K1及反饋控制參數K2，由控制律與被控模型共同組成了下式：

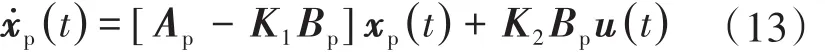
如果被控對象參數已知，則只要滿足下式：

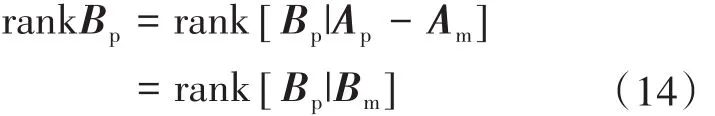
即可求解出參數，從而使得模型與被控對象完全匹配；如果被控對象參數未知或者是緩慢變化的，則可以通過某種非線性映射來調節參數K1和K2，最終使得下式成立：

從而使得下式成立：

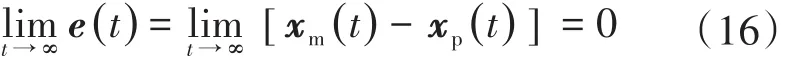
基于Lyapunov穩定理論的模型參考自適應控制，其控制律使用以下兩式[9]：

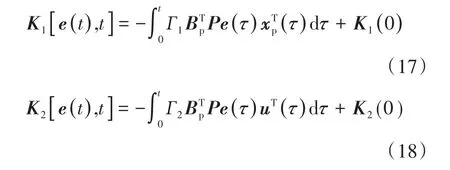
其中

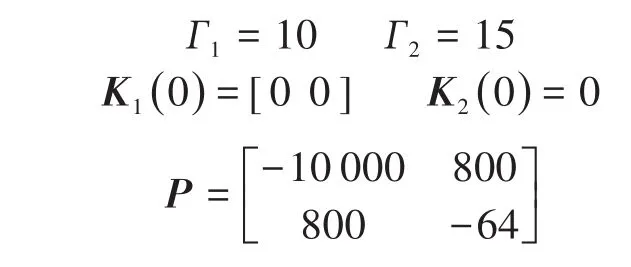
基于Lyapunov穩定理論的模型參考自適應控制對單位階躍響應及正弦曲線的跟蹤情況如圖3、圖4所示。算法的優點在于即使建模參數與模型參數不一致或者模型參數發生漂變也能應對，但是其初期的跟蹤確實存在一定延遲，并且在進行單位階躍響應跟蹤時存在一定超調量，雖然不明顯，但是在節氣門控制中是應該盡量避免的。當然，對控制算法參數進行調節可以避免超調的產生，但卻是以犧牲響應時間為代價的。

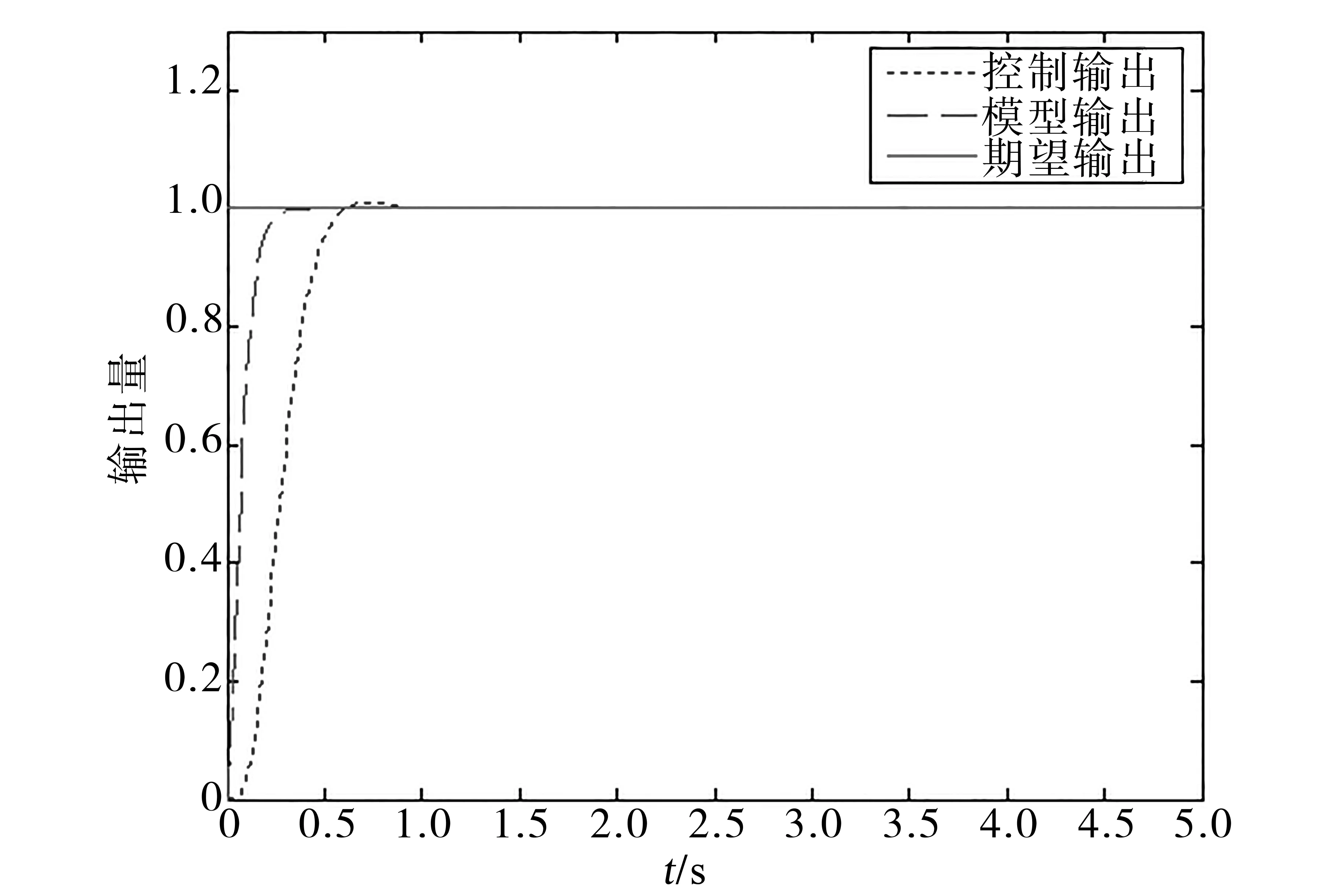
圖3 模型參考自適應控制單位階躍響應Fig.3 Unit step response of model reference adaptive control

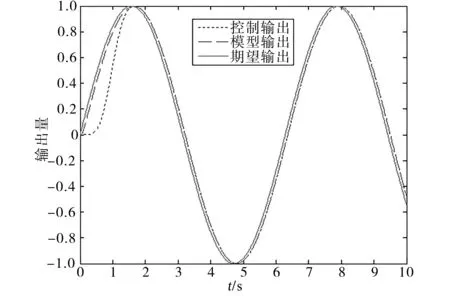
圖4 模型參考自適應控制正弦跟蹤曲線Fig.4 Sine tracking curves with model reference adaptive control

4 模型跟蹤變結構算法

4.1 滑模變結構算法

滑模變結構算法是20世紀50年代所提出的一種可以應對非線性控制的簡單有效方法。但滑模變結構算法在提出之初由于技術條件和控制手段的限制并沒有得到廣泛的關注。近年來，隨著電腦控制速度的提升，此算法開始受到了廣泛關注。特別是我國的控制專家高為炳院士提出了指數趨近律[10]，很大程度緩解了算法的高頻振動，使得算法可以方便應用于實踐。

滑模變結構控制算法需要尋求滑模面，當系統被控制到滑模面后，就會被吸附，從而沿著滑模面趨近到原點。因此，滑模變結構算法是大范圍漸進穩定的。

4.2 模型匹配與模型跟蹤的區分

為了說明本文所提出的算法，特將模型匹配與模型跟蹤的結構繪至圖5和圖6。模型匹配算法是模型參考自適應控制的原理，其控制的基礎是通過控制律來改變系統的前饋及反饋系數，從而使得控制后的被控對象與參考模型精確匹配。而模型跟蹤的目的在于最終使得誤差e趨向于零，而并不在乎模型與對象是否達到了完全一致。這種邏輯的優勢在于設計之初就考慮到了如果系統存在擾動或者建模不準確的因素之后，仍然可以進行有效控制。所以系統可以不過多考慮參考模型本身的參數和結構，只對輸出結果進行有效跟蹤。為了配合此結構所具有的優勢，在圖6的控制律處使用適合非線性控制的滑模變結構控制算法。

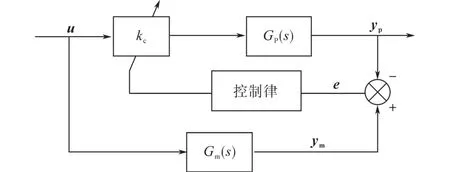
圖5 模型匹配算法結構Fig.5 Structure of model matching algorithm

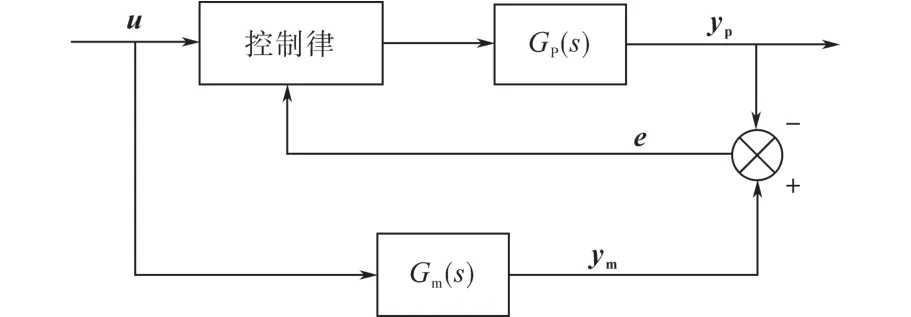
圖6 模型跟蹤算法結構Fig.6 Structure of model tracking algorithm

4.3 模型跟蹤變結構算法

模型跟蹤變結構算法在圖6的控制律處使用積分滑模變結構控制算法。參考模型及被控系統采用式（12）、式（10）的狀態空間表示法。

滑模函數如下式：

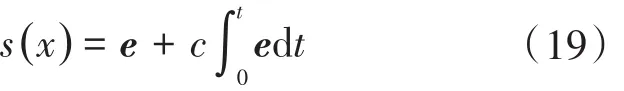
趨近律采用：

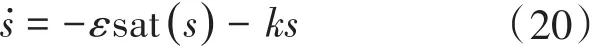
其中

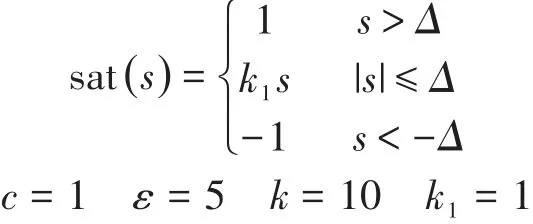
式中：Δ為飽和層厚度。

控制律推導過程如下：

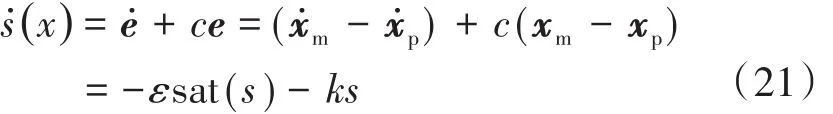
將模型及系統的狀態方程代入得到：

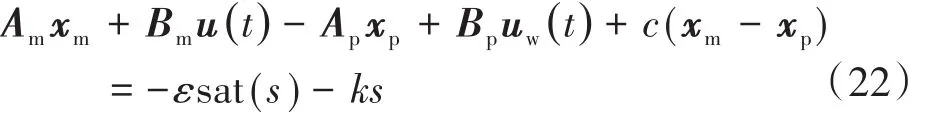
從而可以解出控制律：

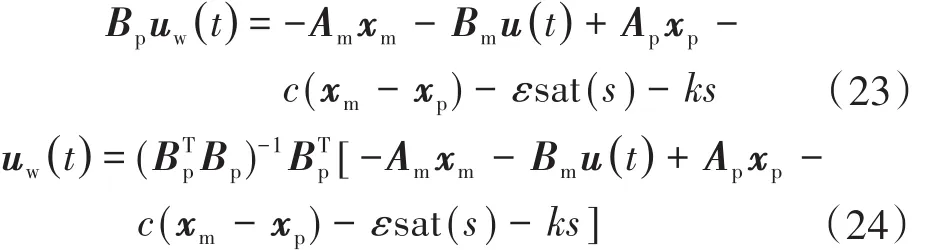
4.4 模型跟蹤變結構算法控制結果分析

圖7和圖8分別為模型跟蹤算法單位階躍響應和模型跟蹤算法正弦跟蹤曲線。

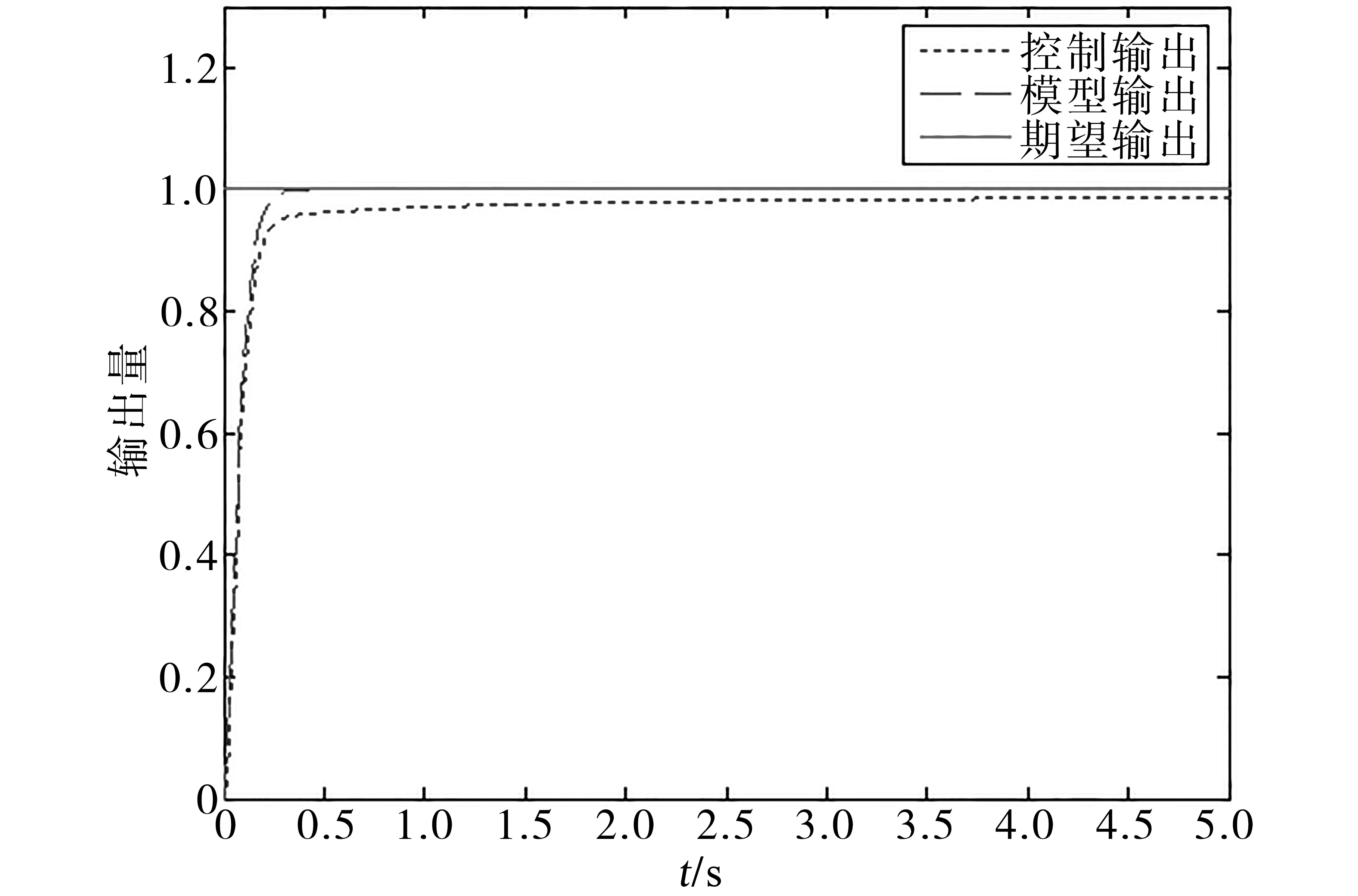
圖7 模型跟蹤算法單位階躍響應Fig.7 Unit step response of model tracking algorithm

通過圖7、圖8與圖3、圖4對比可以得出，模型跟蹤變結構算法在輸出跟蹤上的速度明顯優于模型參考自適應控制，但是在最終的跟蹤精度上不如模型參考自適應控制，這是由于本文所采用的趨近律所導致的。滑模算法在到達滑模面后會做高頻的穿越抖動，雖然可以提升精度，但高頻抖動會使節氣門遭受損壞。算法中所使用到的飽和函數可以使系統到達滑模面后不做抖動，但卻相當于把滑模面做成了一個有一定厚度的滑模曲面空間，從而對跟蹤精度進行了妥協。這種妥協不僅在響應時間上得到了補償，關鍵是在系統建模不準確時依然可以保障系統的穩定性。

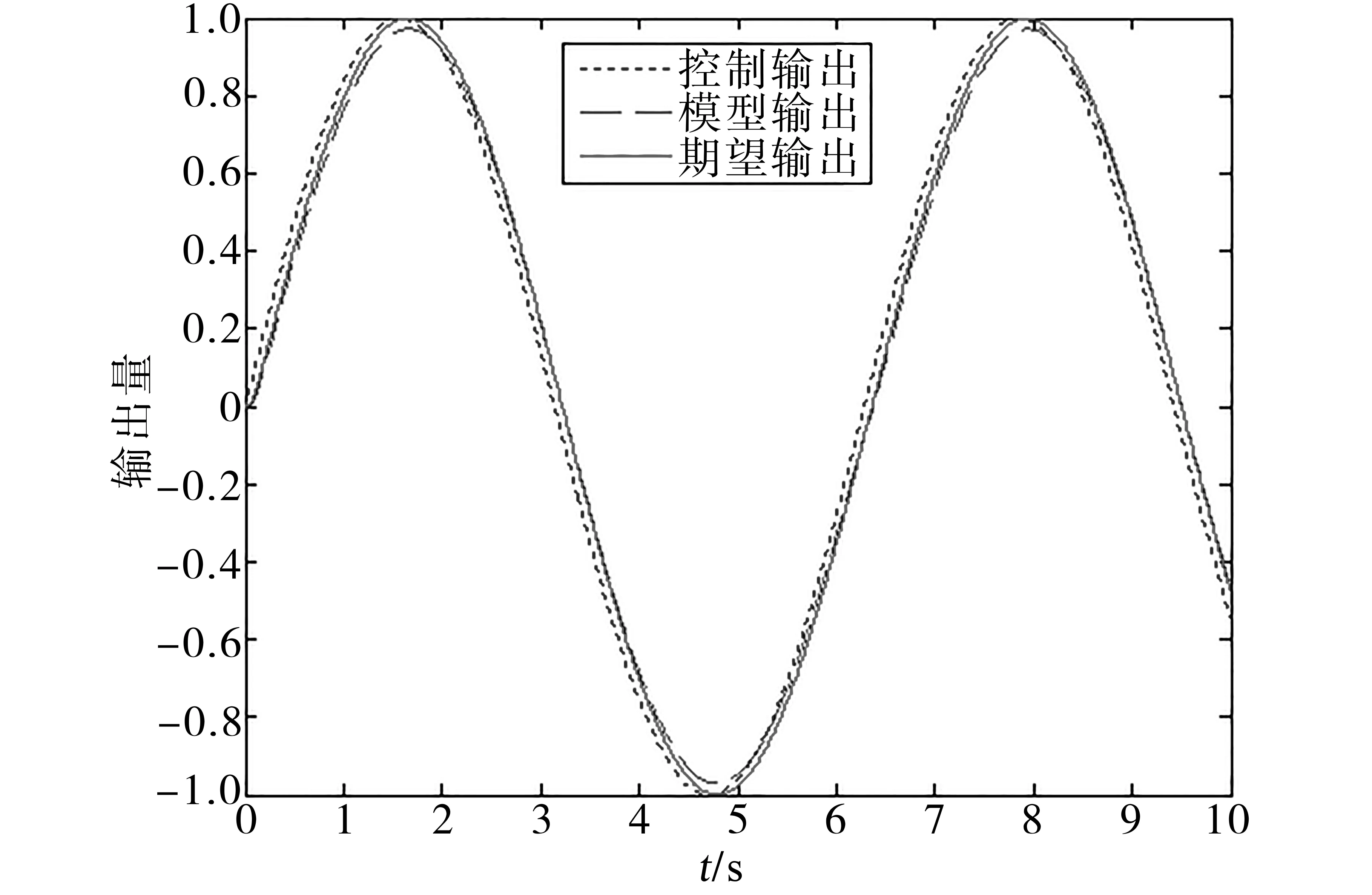
圖8 模型跟蹤算法正弦跟蹤曲線Fig.8 Sine tracing curves of model tracing algorithm

4.5 模型跟蹤變結構算法魯棒性分析

模型參考自適應控制算法與模型跟蹤變結構算法在系統參數發生漂變時都表現出了優良的適應性。但是當存在系統未建模擾動或各種非線性擾動時，模型跟蹤變結構算法表現出了更為強大的魯棒性能。

設Lyapunov函數為

采用式（20）的趨近律可知：s>0時，s?<0；s<0時，s?>0。因此得到：

所以滑模變結構算法滑模面的特點本身就保證了系統是穩定的。

20世紀80年代，Rohrs在研究Lyapunov模型參考自適應控制時發現，當系統受到擾動時，Lyapunov函數導數的半負定性就很難保障，所以系統就可能會失去穩定性，甚至連有界性也很難保障。為了使得算法更具代表性，本文使用Rohrs研究時所使用的模型及擾動函數。

圖9～圖12是使用兩種算法來跟蹤輸入曲線r（t）時的跟蹤誤差，通過對比可以看出，模型參考自適應控制在極端情況下會導致輸出誤差不斷增大，從而喪失穩定性。但模型跟蹤算法在相同情況下卻表現出了強大的魯棒性能。

圖9 模型參考自適應算法r（t）=4.3的誤差曲線Fig.9 Error curve of model reference adaptive algorithm r（t）=4.3

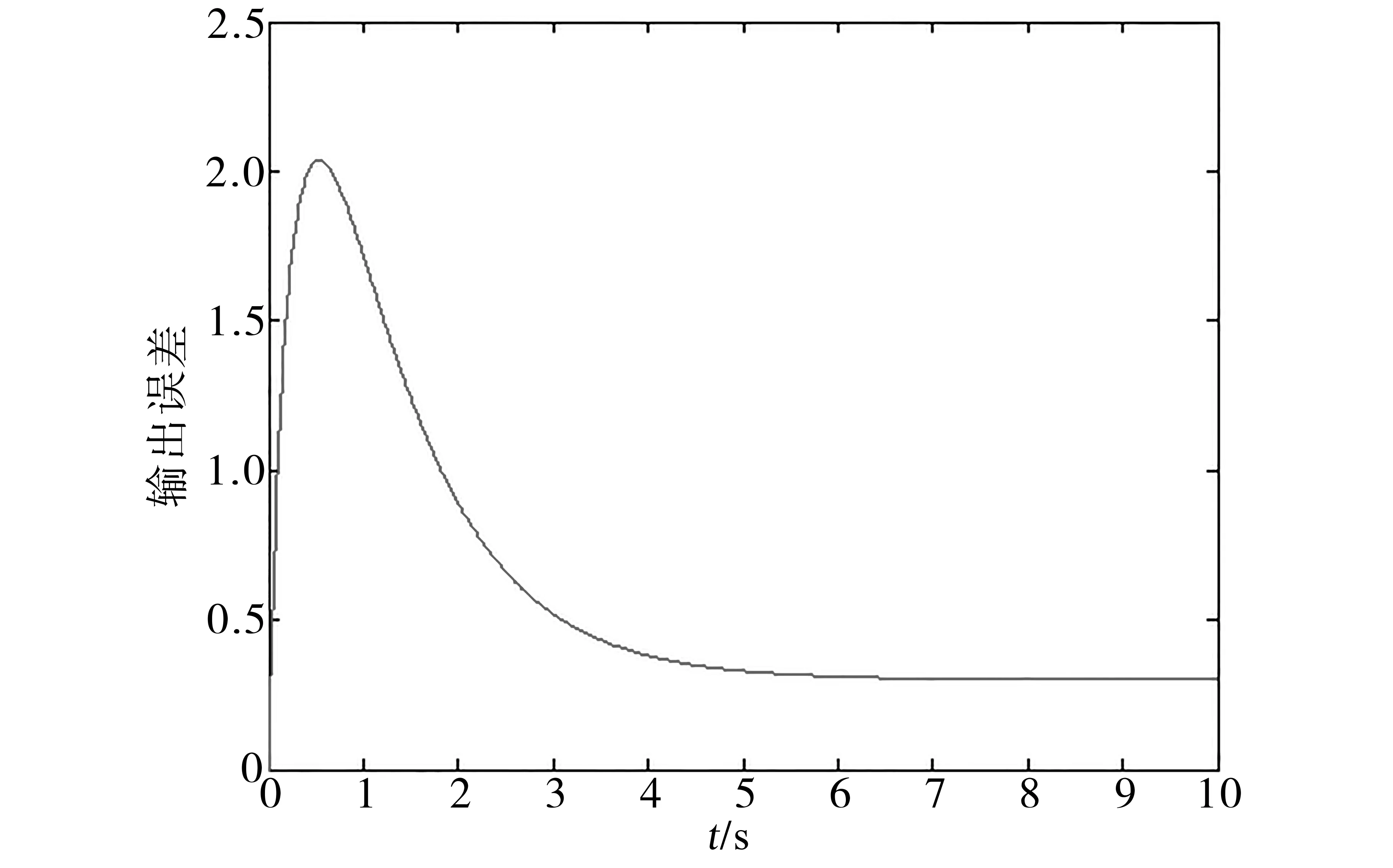
圖10 模型跟蹤算法r（t）=4.3的誤差曲線Fig.10Error curve of model tracking algorithm r（t）=4.3

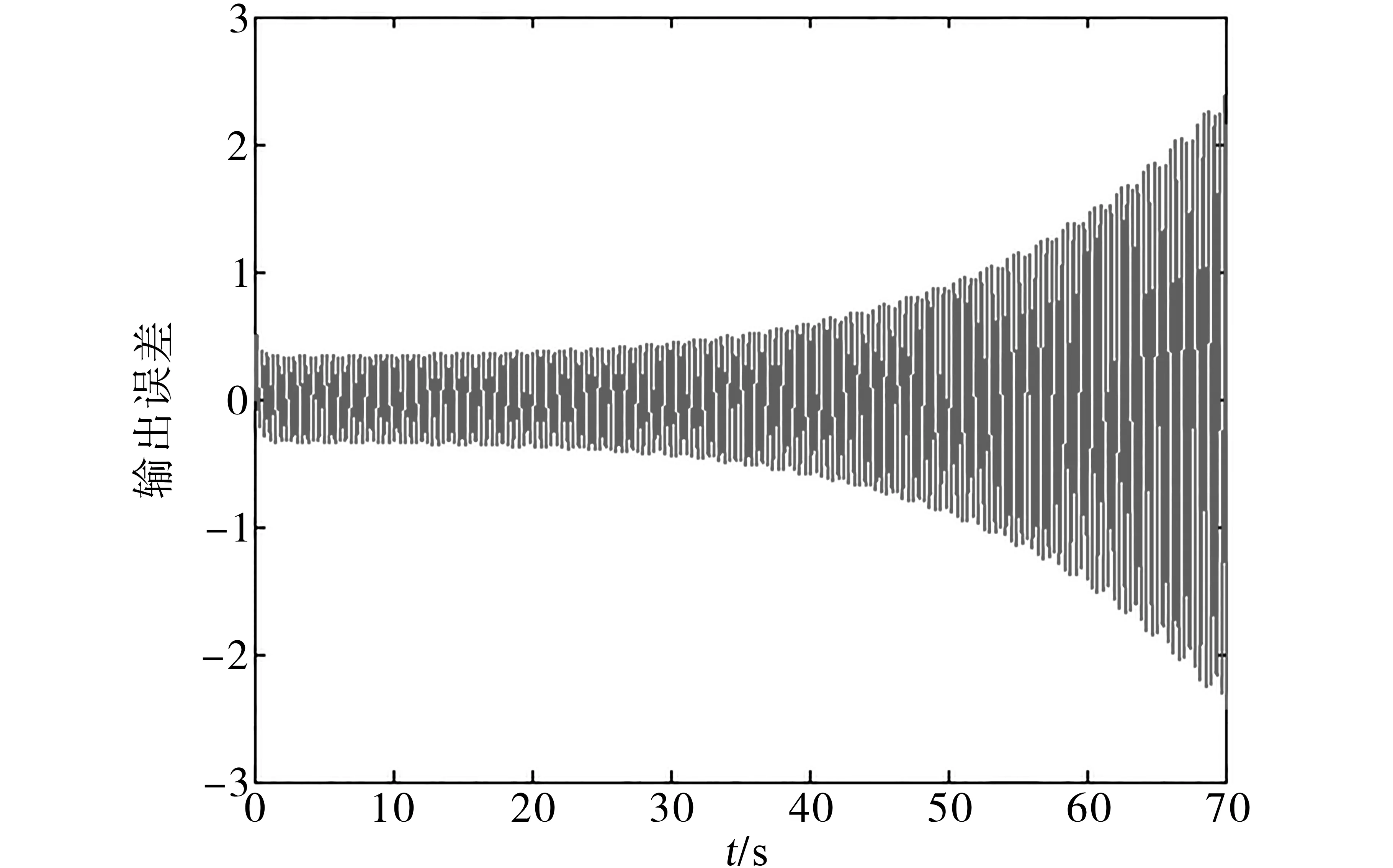
圖11 模型參考自適應算法r（t）=1.8sin（16.1t）的誤差曲線Fig.11 Error curve of model reference adaptive algorithm r（t）=1.8sin（16.1t）

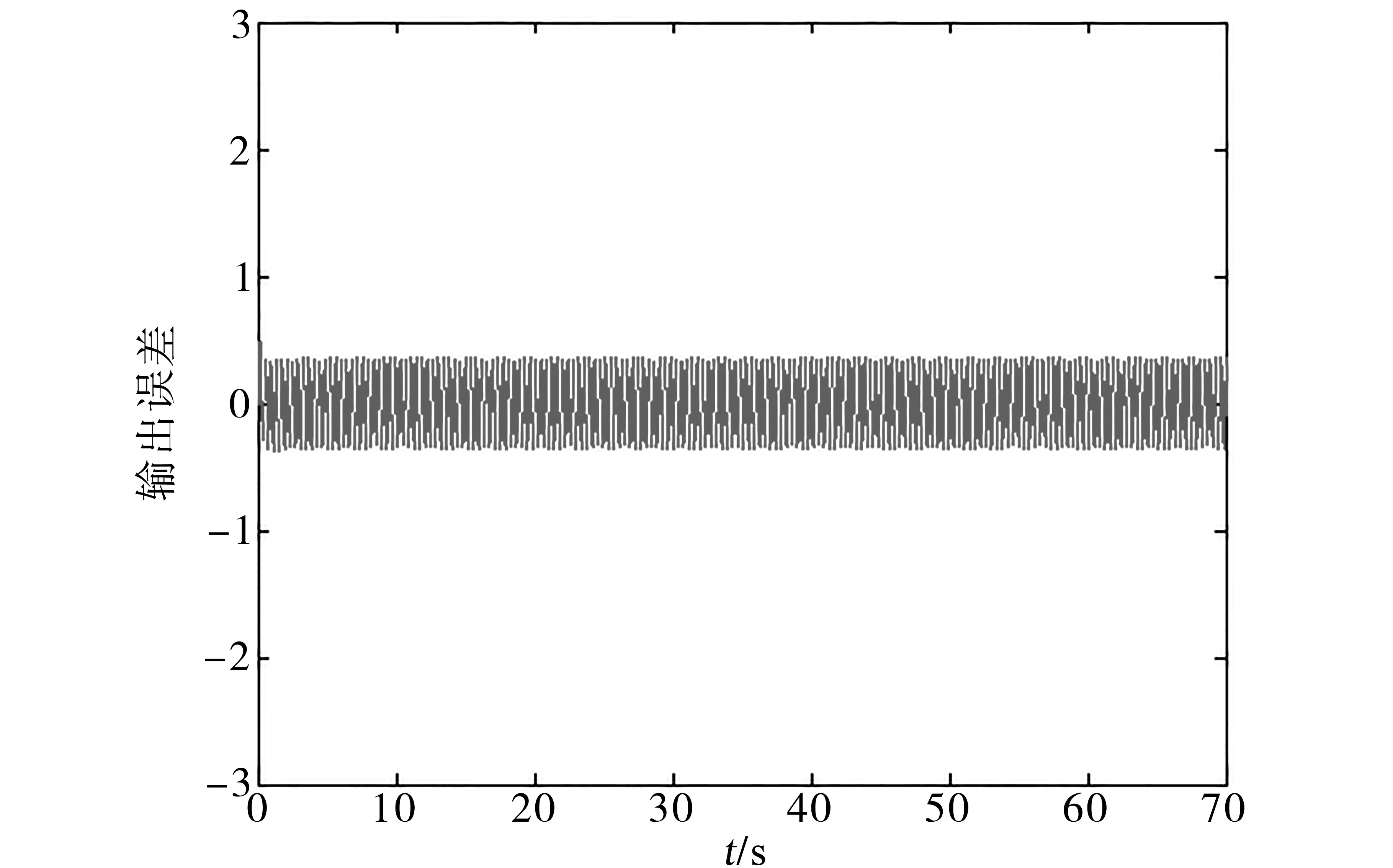
圖12 模型跟蹤算法r（t）=1.8sin（16.1t）的誤差曲線Fig.12Error curve of model tracking algorithm r（t）=1.8sin（16.1t）

電子節氣門工作過程中會受到高頻氣流擾動，為了研究算法的抗干擾能力，在系統中加入了高斯白噪聲，其階躍響應如圖13所示。為了研究參數漂變對系統的影響，將被控對象式（9）的參數進行調整，使得：a1=1，a2=150，a3=3 000，b=6 000，其階躍響應如圖14所示。通過圖13、圖14可以看出，系統在受到擾動以及參數發生漂變時，依然能夠得到理想的控制效果。

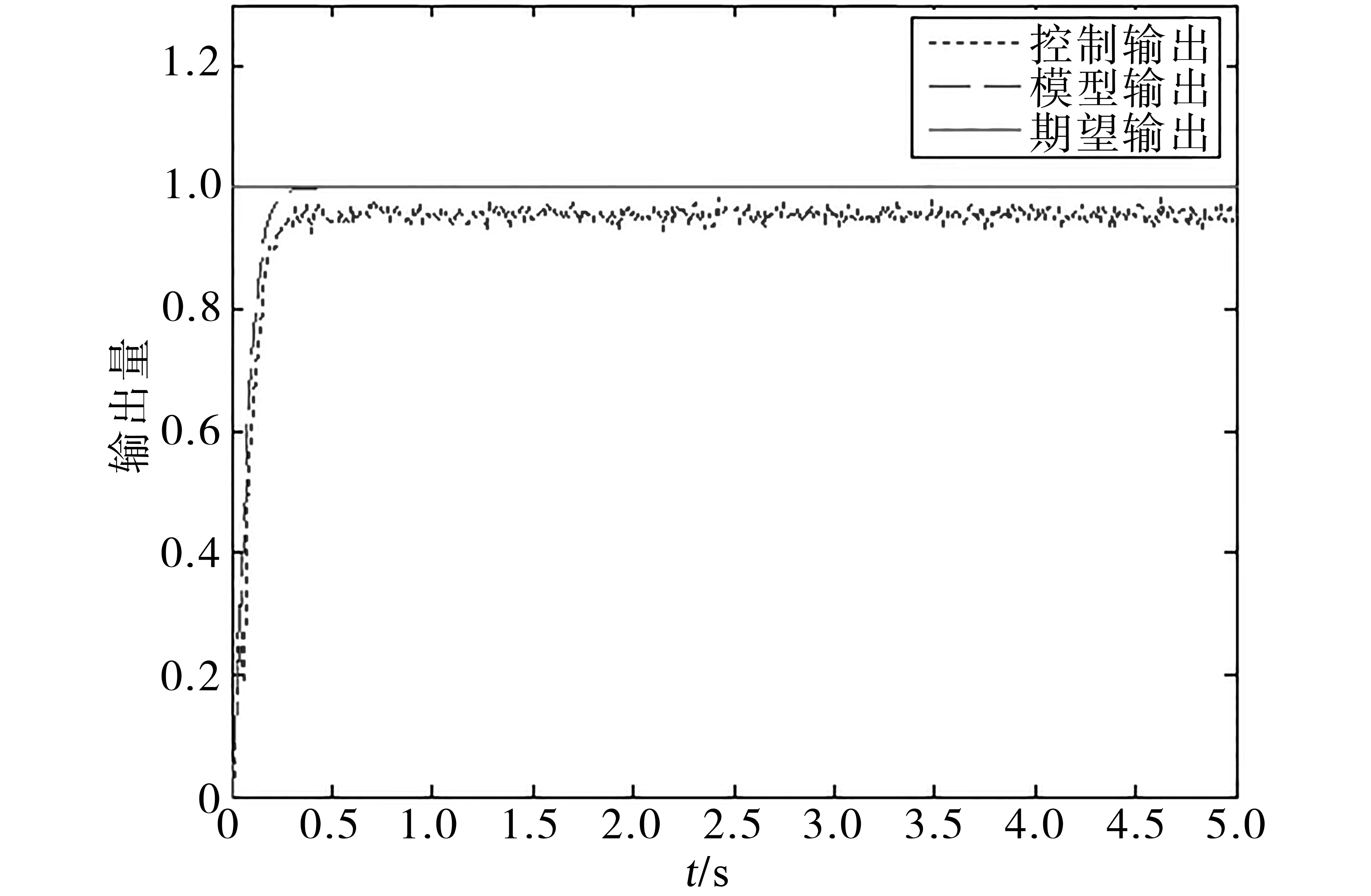
圖13 模型跟蹤算法在加入噪聲后的響應Fig.13 Response of model tracking algorithm after adding noise

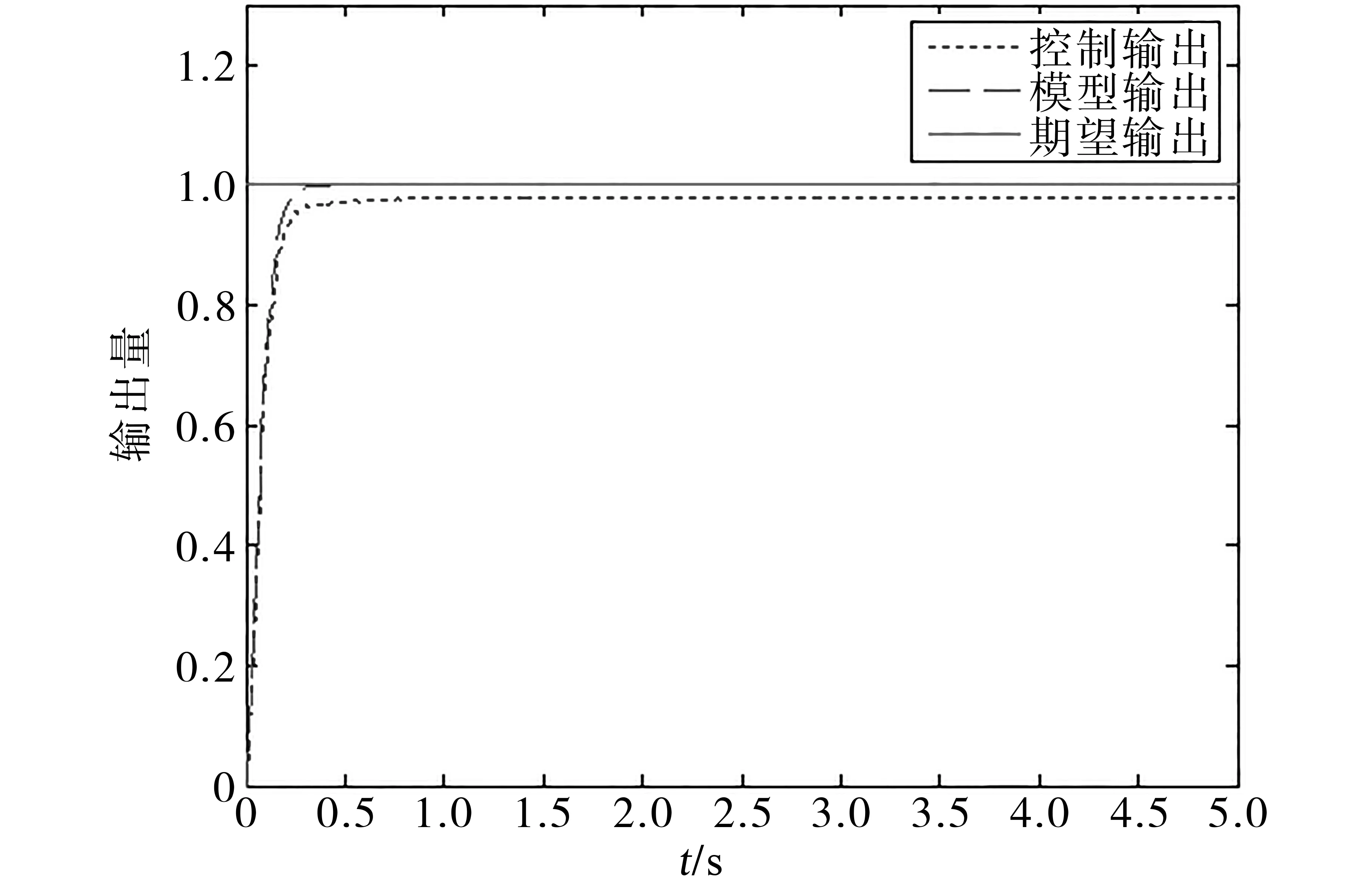
圖14 模型跟蹤算法在被控對象參數發生改變時的響應Fig.14 Response of model tracking algorithm when parameters changed

5 結論

本文針對目前電子節氣門控制算法中存在的不能完美應對模型參數漂變的問題，提出了使用模型跟蹤變結構算法進行控制的思路。首先建立了電子節氣門的控制模型，使用基于Lyapunov的模型參考自適應算法進行了仿真。通過仿真可以看出，模型參考自適應算法在跟蹤單位階躍函數和正弦函數時均有一定的遲滯。

在模型參考自適應控制的原理基礎上，提出了模型跟蹤變結構控制算法，并進行仿真與模型參考自適應算法對比，得出模型跟蹤變結構算法跟蹤精度稍低，但跟蹤延遲減小的結論。

為了將兩種算法魯棒性進行對比，本文采用經典模型及參數進行仿真，得出模型跟蹤變結構算法具有較強魯棒性的結論。因此，在電子節氣門控制過程中，使用模型跟蹤變結構算法以2%左右的穩態誤差換取延遲的減少和魯棒性的增強是合適的。最后，對系統加入噪聲及參數漂變的情況進行了仿真研究，證明了模型跟蹤變結構算法的有效性。