北斗系統(tǒng)星載原子鐘周期性波動(dòng)的頻譜分析校正方法*

李驍逸，龔 航，彭 競(jìng)，于美婷，孫廣富

(國(guó)防科技大學(xué) 電子科學(xué)學(xué)院， 湖南 長(zhǎng)沙 410073)

系統(tǒng)時(shí)間基準(zhǔn)是衛(wèi)星定位系統(tǒng)實(shí)現(xiàn)定位功能的前提。目前北斗衛(wèi)星導(dǎo)航系統(tǒng)(簡(jiǎn)稱北斗三號(hào)系統(tǒng)，BDS-3)的系統(tǒng)時(shí)間基準(zhǔn)由地面站原子鐘通過(guò)綜合原子時(shí)算法計(jì)算生成。一旦地面站出現(xiàn)異常，系統(tǒng)時(shí)間基準(zhǔn)的生成就會(huì)中斷。為了保證系統(tǒng)時(shí)間基準(zhǔn)的穩(wěn)定可靠，必須降低對(duì)地面站的依賴。

北斗衛(wèi)星導(dǎo)航系統(tǒng)衛(wèi)星載有高精度的國(guó)產(chǎn)新型銣鐘和被動(dòng)型氫原子鐘。根據(jù)北斗三號(hào)系統(tǒng)衛(wèi)星數(shù)目及單個(gè)衛(wèi)星星載原子鐘數(shù)目可知，北斗三號(hào)系統(tǒng)星載原子鐘總數(shù)已經(jīng)超過(guò)100顆。大量的星載原子鐘為北斗三號(hào)系統(tǒng)時(shí)間基準(zhǔn)生成計(jì)算擺脫對(duì)地依賴提供了可能。將星載原子鐘逐步納入系統(tǒng)時(shí)間基準(zhǔn)的計(jì)算，最終實(shí)現(xiàn)完全基于星載原子鐘的系統(tǒng)時(shí)間基準(zhǔn)生成是衛(wèi)星定位系統(tǒng)時(shí)間基準(zhǔn)生成的發(fā)展方向。

由于受到太空環(huán)境的影響，星載原子鐘進(jìn)入軌道后的實(shí)際性能與地面鐘存在較大差距。目前已有的研究探明了衛(wèi)星原子鐘性能受到太空環(huán)境負(fù)面影響的主要表現(xiàn)為鐘差數(shù)據(jù)中的周期性波動(dòng)[1-3]。Kenneth等指出星載原子鐘鐘差數(shù)據(jù)中存在的周期性波動(dòng)與衛(wèi)星的軌道周期有一定一致性但又未嚴(yán)格符合，同時(shí)還與日食周期、測(cè)量性能等多種因素相關(guān)[4]。對(duì)于北斗二號(hào)(BDS-2)衛(wèi)星星載原子鐘鐘差數(shù)據(jù)的研究表明，不同的原子鐘對(duì)工作環(huán)境的敏感程度不同，由此導(dǎo)致其鐘差數(shù)據(jù)受到環(huán)境干擾而產(chǎn)生周期性波動(dòng)時(shí)，其周期性波動(dòng)的周期和幅度都各不相同[5-7]。雖然北斗三號(hào)系統(tǒng)的星載原子鐘相比于北斗二號(hào)系統(tǒng)已經(jīng)有了顯著的性能提升，但是鐘差數(shù)據(jù)中的周期性波動(dòng)依然存在[8-9]。根據(jù)上述已有研究可以確定，不論何種衛(wèi)星類型或原子鐘類型，其鐘差數(shù)據(jù)都存在周期性波動(dòng)。在未能消除周期性波動(dòng)前不應(yīng)將星載原子鐘納入系統(tǒng)時(shí)間基準(zhǔn)的計(jì)算，以攜帶周期性波動(dòng)的衛(wèi)星鐘差進(jìn)行系統(tǒng)時(shí)間基準(zhǔn)計(jì)算會(huì)將上述波動(dòng)引入系統(tǒng)時(shí)間。對(duì)于這一問(wèn)題，本文提出了一種對(duì)鐘差數(shù)據(jù)中的周期性波動(dòng)進(jìn)行校正的方法。該方法不能提升衛(wèi)星原子鐘的性能，但卻可以提升原子鐘輸出的鐘差數(shù)據(jù)的性能，從而避免將衛(wèi)星原子鐘的周期性波動(dòng)引入系統(tǒng)時(shí)間。本文基于國(guó)際衛(wèi)星導(dǎo)航服務(wù)組織(International GNSS Service, IGS)對(duì)北斗系統(tǒng)衛(wèi)星由2020年5月1日至5月30日之間連續(xù)30 d的鐘差觀測(cè)數(shù)據(jù)計(jì)算了北斗系統(tǒng)衛(wèi)星的幅頻特性、相頻特性及頻率穩(wěn)定度性能，并提出了消除星載原子鐘鐘差數(shù)據(jù)中周期性波動(dòng)的方法。

1 北斗系統(tǒng)星載原子鐘特性分析

1.1 時(shí)域特性分析

能夠體現(xiàn)原子鐘時(shí)域特性的因素包括相位、頻率和頻率漂移。通常情況下，原子鐘的相位差數(shù)據(jù)(即鐘差)模型采用包含這三個(gè)因素的二次多項(xiàng)式模型。

x(t)=x0+y0t+0.5z0t2+ε(t)

(1)

其中：x0和y0是相位和頻率偏差；z0表示頻率偏差的線性變化，通常稱為老化或頻率漂移；ε(t)是隨機(jī)噪聲；t為鐘差數(shù)據(jù)x(t)的采樣時(shí)間序列。

但是星載原子鐘的相位差數(shù)據(jù)還包含多種周期性波動(dòng)。星載原子鐘周期性波動(dòng)項(xiàng)的來(lái)源較為復(fù)雜，受到地月運(yùn)行、地球公轉(zhuǎn)、相對(duì)論及溫度光壓和相對(duì)論效應(yīng)等多種因素的影響，在原子鐘相位差數(shù)據(jù)的常規(guī)表達(dá)式中需要增加周期項(xiàng)來(lái)表達(dá)星載原子鐘的周期性波動(dòng)。因此星載原子鐘的相位差數(shù)據(jù)被描述為以下等式：

(2)

其中，Al是周期性波動(dòng)的振幅，ωl是周期性波動(dòng)的頻率，φl(shuí)是周期性波動(dòng)正弦變化的相移。

1.2 頻率穩(wěn)定度分析

本文首先對(duì)衛(wèi)星鐘差數(shù)據(jù)進(jìn)行了預(yù)處理，消除了相位跳變、頻率跳變和野值，然后以阿倫偏差來(lái)計(jì)算各星載原子鐘的頻率穩(wěn)定度。各衛(wèi)星進(jìn)行校正前的原始頻率穩(wěn)定度如圖1所示。

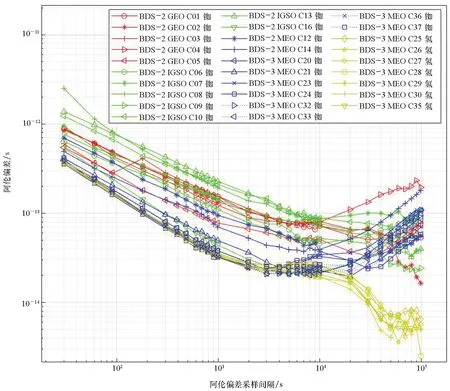
圖1 阿倫偏差計(jì)算結(jié)果Fig.1 Calculated results of Allan deviation

圖1中橫軸為頻率穩(wěn)定度采樣間隔，縱軸為頻率穩(wěn)定度計(jì)算結(jié)果。其中，紅色曲線為地球同步軌道(GEOstationary, GEO)衛(wèi)星頻率穩(wěn)定度，藍(lán)色曲線為星載原子鐘為銣鐘的中軌道(MEdium Orbit, MEO)地球衛(wèi)星頻率穩(wěn)定度，黃色曲線為星載原子鐘為氫鐘的MEO衛(wèi)星頻率穩(wěn)定度，綠色曲線為傾斜地球同步軌道(Inclined GeoSynchronous Orbit, IGSO)衛(wèi)星頻率穩(wěn)定度。

頻率穩(wěn)定度計(jì)算表明，衛(wèi)星軌道類型對(duì)星載原子鐘的性能具有顯著影響。在星載原子鐘同為銣鐘的情況下，IGSO衛(wèi)星的頻率穩(wěn)定度在萬(wàn)秒以下穩(wěn)定度計(jì)算步長(zhǎng)上比MEO衛(wèi)星和GEO衛(wèi)星更差，而在萬(wàn)秒以上數(shù)值則與MEO衛(wèi)星和GEO衛(wèi)星相當(dāng)。GEO衛(wèi)星的短期穩(wěn)定度弱于MEO強(qiáng)于IGSO，萬(wàn)秒以上穩(wěn)定度與MEO和IGSO相當(dāng)。MEO衛(wèi)星在萬(wàn)秒以下平均時(shí)間中具有最好的頻率穩(wěn)定度性能，但是在萬(wàn)秒以上平均時(shí)間下性能比GEO衛(wèi)星差。

比較三類衛(wèi)星的頻率穩(wěn)定度性能可以發(fā)現(xiàn)，北斗三號(hào)系統(tǒng)的MEO衛(wèi)星具有最集中的性能分布。而北斗二號(hào)的GEO衛(wèi)星、IGSO衛(wèi)星和MEO衛(wèi)星的性能分布更加松散，且北斗二號(hào)的C12、C14號(hào)MEO衛(wèi)星的性能相比于GEO衛(wèi)星和IGSO衛(wèi)星優(yōu)勢(shì)并不顯著。這一結(jié)果表明，即使同為銣鐘，北斗三號(hào)系統(tǒng)的銣鐘性能也優(yōu)于北斗二號(hào)系統(tǒng)的銣鐘。

頻率穩(wěn)定度計(jì)算結(jié)果也表明，星載原子鐘的類型對(duì)星載原子鐘的性能也具有顯著影響。除去搭載銣鐘的衛(wèi)星，北斗三號(hào)系統(tǒng)還擁有部分星載鐘為氫鐘的MEO衛(wèi)星。這一類衛(wèi)星不僅萬(wàn)秒以下穩(wěn)定度和銣鐘衛(wèi)星中短期穩(wěn)定度性能最好的北斗三號(hào)銣鐘MEO衛(wèi)星相當(dāng)，在萬(wàn)秒及更長(zhǎng)的平均時(shí)間中更是表現(xiàn)出了所有衛(wèi)星中最好的性能。

計(jì)算結(jié)果顯示MEO衛(wèi)星上的氫鐘比銣鐘在萬(wàn)秒及更長(zhǎng)采樣間隔下的頻率穩(wěn)定度性能上具有極大的性能優(yōu)勢(shì)。計(jì)算結(jié)果同時(shí)顯示，在同為銣鐘的情況下，IGSO衛(wèi)星和GEO衛(wèi)星在天及更長(zhǎng)的采樣間隔上的頻率穩(wěn)定度性能優(yōu)于MEO衛(wèi)星，這表明IGSO衛(wèi)星軌道和GEO衛(wèi)星軌道比MEO更有利于保持原子鐘的長(zhǎng)期頻率穩(wěn)定度性能。因此，將IGSO衛(wèi)星和GEO衛(wèi)星上的銣鐘也更換為氫鐘是值得嘗試的，IGSO衛(wèi)星和GEO衛(wèi)星上的氫原子鐘極有可能獲得比MEO衛(wèi)星氫鐘更好的長(zhǎng)期頻率穩(wěn)定度性能。

由于MEO衛(wèi)星星載被動(dòng)型氫鐘的性能在各個(gè)平均時(shí)間下的頻率穩(wěn)定度都具有最佳性能。在星座自主守時(shí)的設(shè)計(jì)中，應(yīng)當(dāng)以使用被動(dòng)型氫鐘的MEO衛(wèi)星作為綜合原子時(shí)計(jì)算的參考鐘或時(shí)間基準(zhǔn)物理信號(hào)的生成鐘。同時(shí)根據(jù)系統(tǒng)的設(shè)計(jì)指標(biāo)，靈活運(yùn)用IGSO衛(wèi)星、GEO衛(wèi)星和載有銣鐘的MEO衛(wèi)星，根據(jù)具體需求決定這三類衛(wèi)星在聯(lián)合守時(shí)中的權(quán)重。

1.3 頻域特性分析

本文在去除鐘差數(shù)據(jù)的二次趨勢(shì)項(xiàng)之后，對(duì)獲得的鐘差殘差數(shù)據(jù)進(jìn)行快速傅里葉變換獲得衛(wèi)星鐘差的周期特性。由于篇幅限制，本文在所有衛(wèi)星中選擇了13顆衛(wèi)星，使例證包含了全部衛(wèi)星類型和星載原子鐘類型。本文選擇GEO衛(wèi)星C02(銣鐘)、C05(銣鐘)，IGSO衛(wèi)星C07(銣鐘)、C13(銣鐘)，北斗二號(hào)系統(tǒng)的MEO衛(wèi)星C11(銣鐘)、C12(銣鐘)以及北斗三號(hào)系統(tǒng)的MEO衛(wèi)星C23(銣鐘)、C36(銣鐘)、C25(氫鐘)、C29(氫鐘)為例。衛(wèi)星鐘差幅頻曲線如圖2、圖3所示。

從圖2和圖3可以看出，北斗二號(hào)系統(tǒng)及北斗三號(hào)系統(tǒng)所有類型的各衛(wèi)星均有不同程度的24 h、12 h、8 h、6 h等多種周期項(xiàng)。比較北斗二號(hào)系統(tǒng)各衛(wèi)星與北斗三號(hào)系統(tǒng)各衛(wèi)星可以發(fā)現(xiàn)，北斗二號(hào)系統(tǒng)各衛(wèi)星星載原子鐘更容易受到多重外部因素的影響且自身噪聲更大，導(dǎo)致周期性波動(dòng)項(xiàng)不僅更多，且在幅頻曲線中難以顯著地體現(xiàn)出來(lái)。北斗三號(hào)系統(tǒng)各衛(wèi)星原子鐘自身噪聲較小導(dǎo)致其周期性波動(dòng)項(xiàng)相對(duì)北斗二號(hào)系統(tǒng)格外顯著，同時(shí)其周期性波動(dòng)項(xiàng)數(shù)量更少，表明對(duì)環(huán)境因素也具有更好的耐受性。由于北斗系統(tǒng)的授時(shí)精度在20 ns左右[10]，為了滿足衛(wèi)星定位系統(tǒng)的精度需求，在進(jìn)行周期性波動(dòng)項(xiàng)校正時(shí)，不能僅僅計(jì)算少數(shù)幾個(gè)主要周期項(xiàng)，而應(yīng)以周期性波動(dòng)幅度為考慮因素。本文將幅頻曲線中所有幅值大于0.01 ns的周期項(xiàng)全部作為校正目標(biāo)。

(a) GEO C02 銣鐘(a) GEO C02 Rb (b) GEO C05 銣鐘(b) GEO C05 Rb (c) IGSO C07 銣鐘(c) IGSO C07 Rb

(a) MEO C23 銣鐘(a) MEO C23 Rb (b) MEO C36 銣鐘(b) MEO C36 Rb

2 北斗三號(hào)系統(tǒng)星載原子鐘周期性波動(dòng)校正

2.1 周期性波動(dòng)校正時(shí)域模型

本文基于式(2)所示星載原子鐘鐘差模型公式，構(gòu)建如式(3)所示的星載原子鐘相位差數(shù)據(jù)校正模型。

(3)

其中：x′(t)為經(jīng)過(guò)校正后的鐘差數(shù)據(jù)；Al為求得的各周期性波動(dòng)項(xiàng)幅值；ω′為求得的各周期性波動(dòng)項(xiàng)頻率；φ′l為求得的各周期性波動(dòng)正弦變化的相移。

具體方法為，在式(2)所示的星載原子鐘鐘差數(shù)據(jù)時(shí)域模型上添加周期項(xiàng)，使新添加的周期項(xiàng)與星載原子鐘固有的周期項(xiàng)頻率幅度相同而相位相反，從而將衛(wèi)星鐘差固有的周期性波動(dòng)抵消。通過(guò)傅里葉變換求得精確的A′l、ω′l、φ′l數(shù)值，即可通過(guò)式(3)消除星載原子鐘鐘差數(shù)據(jù)內(nèi)的周期性波動(dòng)項(xiàng)，同時(shí)無(wú)須考慮該周期性波動(dòng)的成因和來(lái)源。

2.2 校正后鐘差數(shù)據(jù)頻率穩(wěn)定度分析

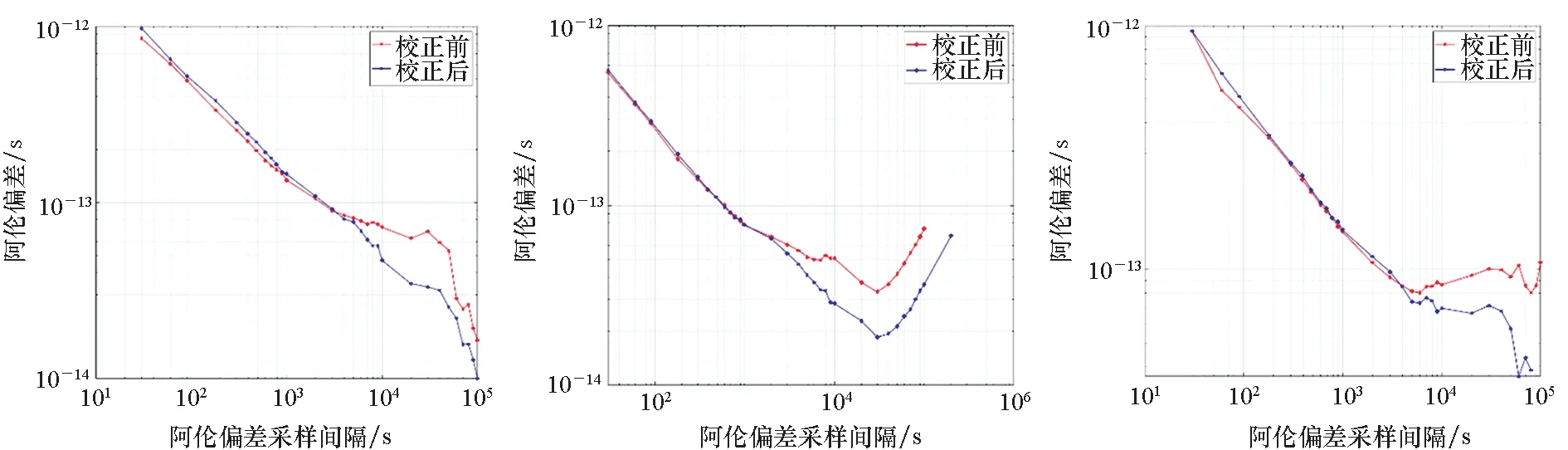
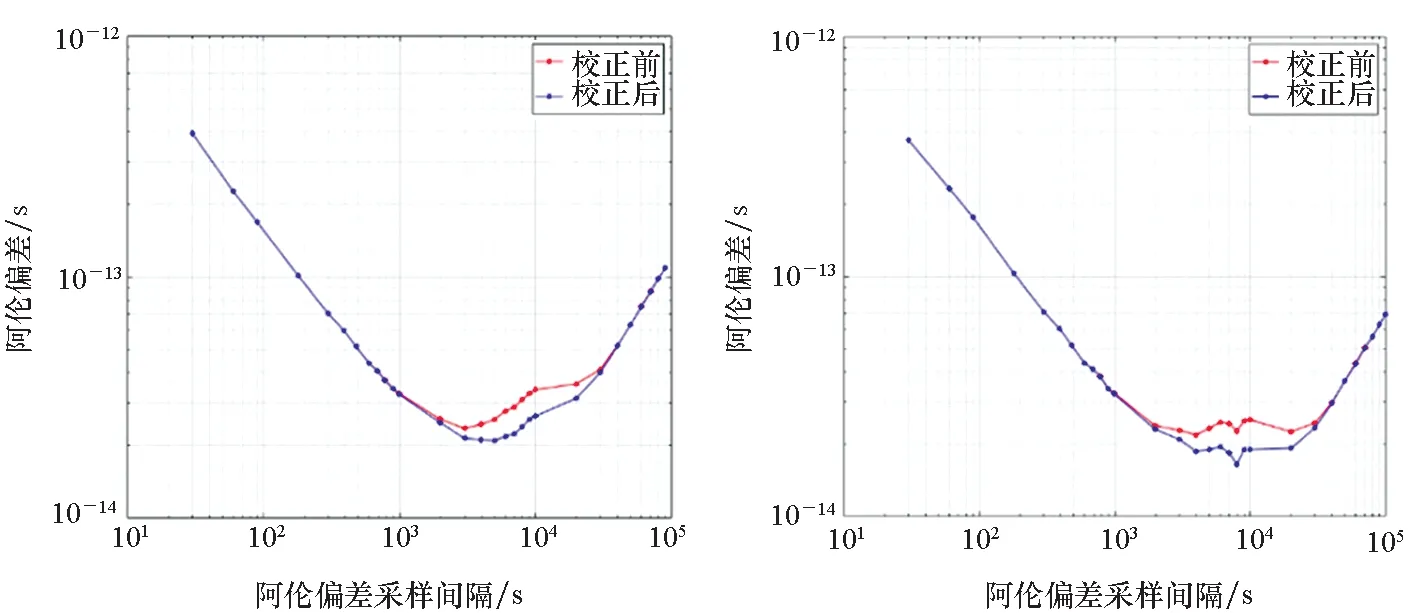
圖4和圖5分別為校正前后的北斗二號(hào)系統(tǒng)和北斗三號(hào)系統(tǒng)衛(wèi)星星載原子鐘鐘差數(shù)據(jù)頻率穩(wěn)定度計(jì)算結(jié)果對(duì)比。

(a) GEO C02 銣鐘(a) GEO C02 Rb (b) GEO C05 銣鐘(b) GEO C05 Rb (c) IGSO C07 銣鐘(c) IGSO C07 Rb

(a) MEO C23 銣鐘(a) MEO C23 Rb (b) MEO C36 銣鐘(b) MEO C36 Rb

由圖4和圖5可以看出，所有的衛(wèi)星都產(chǎn)生了顯著的性能提升效果。從衛(wèi)星軌道類型上來(lái)看，GEO衛(wèi)星的性能提升效果最佳，其次是IGSO衛(wèi)星，MEO衛(wèi)星的提升效果在三種衛(wèi)星中最弱。從原子鐘類型上來(lái)看，北斗二號(hào)系統(tǒng)銣鐘的性能提升效果最佳，其次是北斗三號(hào)系統(tǒng)的銣鐘，北斗三號(hào)系統(tǒng)的氫鐘性能提升最弱。但是不論是何種軌道類型、何種原子鐘類型的衛(wèi)星，校正后的穩(wěn)定度曲線都正確地削去了原穩(wěn)定度曲線的異常隆起，校正后的穩(wěn)定度曲線有較大改善。

穩(wěn)定度數(shù)據(jù)的具體提升數(shù)值如表1所示。

表1 星載原子鐘性能提升效果

由表1可以看出，所有衛(wèi)星的頻率穩(wěn)定度性能都獲得了顯著的提升，萬(wàn)秒頻率穩(wěn)定度提升范圍在14%～45%不等。其中，C02衛(wèi)星的提升效果最為顯著，萬(wàn)秒頻率穩(wěn)定度由7.2×10-14s提升到4.6×10-14s，在10萬(wàn)秒頻率穩(wěn)定度已達(dá)到1.0×10-14s，與地面站銫原子鐘相當(dāng)。其余各衛(wèi)星在萬(wàn)秒穩(wěn)定度及最佳穩(wěn)定度步長(zhǎng)下的穩(wěn)定度性能也都達(dá)到了地面站銫原子鐘的性能(萬(wàn)秒頻率穩(wěn)定度7×10-14s，5071A型銫原子鐘)，差于地面站氫鐘(萬(wàn)秒頻率穩(wěn)定度2×10-15s，MHM-2010型氫原子鐘)。

3 結(jié)論

通過(guò)比較校正前后星載原子鐘鐘差數(shù)據(jù)的頻率穩(wěn)定度性能差異，本文所述方法能夠成功消除由衛(wèi)星運(yùn)行環(huán)境引起的衛(wèi)星鐘差數(shù)據(jù)周期性波動(dòng)，提高星載原子鐘鐘差數(shù)據(jù)的計(jì)算性能。通過(guò)該方法校正后，系統(tǒng)中不同軌道類型的衛(wèi)星星載原子鐘的性能都得到了顯著的提升。其中，GEO C05衛(wèi)星星載原子鐘的萬(wàn)秒頻率穩(wěn)定度提升45%，MEO C29衛(wèi)星星載原子鐘的萬(wàn)秒頻率穩(wěn)定度提升30%，IGSO C07衛(wèi)星星載原子鐘的萬(wàn)秒頻率穩(wěn)定度提升20%。通過(guò)本文所述方法的校正，北斗二號(hào)和北斗三號(hào)星載原子鐘普遍達(dá)到了地面站銫鐘的頻率穩(wěn)定度性能，為北斗系統(tǒng)基于星載原子鐘的星座自主守時(shí)提供了支撐。