群時延傅里葉分解模型及其估計方法*

肖志斌，黃仰博，唐小妹，劉增軍，倪少杰

(國防科技大學 電子科學學院， 湖南 長沙 410073)

大部分衛星導航系統采用了直接序列擴頻系統，如美國的GPS、中國的BeiDou、俄羅斯的GLONASS以及歐洲的Galileo等。直接序列擴頻系統通過擴展頻譜提高信號增益，而擴展頻譜后，接收信道帶寬將增大，此時接收通道很難保證理想的幅頻及群時延特性，導航信號會產生畸變，進而產生測距偏差[1-2]，已成為高精度測距的主要誤差源之一。隨著導航系統的現代化，大量現代化導航信號采用了二進制偏移載波(Binary Offset Carrier, BOC)[3]調制技術，部分高階BOC信號帶寬很寬，如AltBOC(15,10)[4]、BOC(15,2.5)[5]等，其受幅頻及群時延非理想特性的影響更明顯。

群時延非理想導致信號畸變，進而產生測距偏差，因此有必要對其進行測量與校準。目前的群時延測量技術主要有兩類：矢量網絡分析儀法[6]以及基于信號自相關函數頻譜分析的群時延估計方法。矢量網絡分析儀法主要通過測量通道的相位特性進而得到通道的群時延特性，矢量網絡分析儀法會存在測量精度與測量分辨率無法同時兼顧的問題[6]。另外，該方法的實施復雜，需要采用一系列外圍設備，如掃頻源、矢量網絡分析儀等，硬件鏈路復雜，測試流程也復雜。且該方法一般適合測量輸入輸出頻段一致的單個通道的群時延特性，對于導航接收機，會存在多個變頻環節，整機存在多個變頻器及多個濾波器，因此測量整機的群時延特性將更為繁雜。

通道群時延特性可以為關于頻率的任意連續函數，可以采用函數級數對任意群時延特性進行描述，這樣任意群時延特性可用一組函數級數的系數表示，群時延的測量可通過估計這些函數級數的系數來實現，此時預先計算并存儲各種群時延分解系數組合下的相關峰波形數據，通過測量信號相關峰并進行相關峰匹配搜索即可對這些系數進行估計。

該方法的可行性主要取決于函數級數的選取，目前比較經典的群時延分解模型是基于泰勒級數展開的分解模型[7]，該模型將任意群時延特性分解為一系列多次項群時延，如1階群時延、2階群時延(拋物線群時延)、3階群時延等，上述模型可以描述實際中的大部分濾波器，比如巴特沃茲、切比雪夫濾波器均表現為線性群時延與二階群時延的疊加，但該模型很難描述群時延具有三角函數特性的濾波器，如聲表面波濾波器。另外該模型分解后的各階群時延仍然沒有明確的物理意義，只是在數學意義上的曲線，不能和相關峰畸變建立直接的聯系，因此無法確定函數分解的階數。

本文通過理論推導分析了三角函數群時延對信號相關峰的影響，發現三角函數群時延對于信號相關峰的影響是產生了一系列多徑信號，且三角函數頻率越高，多徑距離主瓣信號越遠，幅度也越低，影響也越小，高頻的三角函數群時延對信號相關峰的影響可忽略不計。基于此項分析，可以將任意群時延特性進行傅里葉分解，將其分解為有限階數余弦型與正弦型群時延的級聯，經過本文分析，采用3階余弦型群時延和正弦型群時延即可表征大部分通道群時延對信號相關峰的影響，這樣只需要估計這3階余弦型群時延和正弦型群時延的系數即可，此時預先計算并存儲各種群時延傅里葉分解系數組合下的相關峰波形數據，通過測量信號相關峰并進行相關峰匹配搜索即可對這些系數進行估計。

1 三角函數群時延對信號相關峰的影響

三角函數群時延主要分為余弦型群時延和正弦型群時延兩類，余弦型群時延及正弦型群時延可分別表示為：

(1)

(2)

其中，a、b分別為余弦型群時延和正弦型群時延的波動幅度,fp為群時延波動頻率。余弦型群時延傳輸函數可表示為：

Hc(f)=exp[jθcsin(2πTf)]

=cos[θcsin(2πTf)]+sin[θcsin(2πTf)]

(3)

其中，θc=-Ba,T=1/B，利用第一類貝塞爾函數[8-10]可得到：

(4)

根據余弦型群時延傳輸函數分解的結果，正弦型群時延傳輸函數滿足：

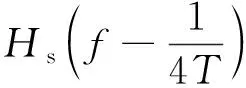
=exp[jθssin(2πTf)]

(5)

即：

(6)

顯然，余弦型群時延τc(f)對信號相關峰的影響是產生了一系列延遲量為kT(k!=0)，幅度為|J-k(θ)| (k!=0)的回波信號；正弦型群時延τs(f)信號相關峰的影響是產生了一系列延遲量為kT(k!=0)，幅度為|J-k(θ)| (k!=0)，相位為kπ/2的回波信號。

2 基于傅里葉級數的通道群時延分解模型

任意通道的傳輸函數可表示為：

H(f)=A(f)exp[jψ(f)]

(7)

其中，A(f)為幅頻響應，ψ(f)為相頻響應。群時延的表達式為：

(8)

假設通道的雙邊帶帶寬為Bf，對τ(f)在通道帶寬范圍內進行傅里葉分解，可得到：

(9)

其中，ci與si為傅里葉系數。

根據前一節的分析結果，第i級余弦型群時延與正弦型群時延的傳輸函數可分別分解為：

(10)

(11)

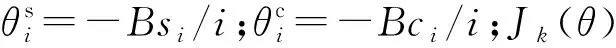
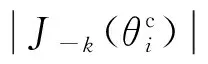
對于BPSK(n)信號，其碼率為fc=1.023nMHz，對應的碼率為Tc=1/fc, 通道帶寬B取為信號雙邊帶帶寬，即B=2fc。顯然，當i/B≥2Tc，即i≥2B/fc=4時，第i級余弦型/正弦型群時延將產生一系列與主相關峰相距超過2倍碼片的回波信號，且幅度很小，而主相關峰主瓣寬度為兩個碼片，因此這些回波信號不會對主相關峰產生影響。圖1以碼率fc=10.23 MHz的擴頻信號為例，給出了第4級余弦群時延τ(f)=c·cos(4πf/fc)對信號相關峰的影響，對應群時延波動周期為fc/2=5.115 MHz，c為100 ns。顯然，該群時延僅產生了距離主相關峰兩倍碼片的回波信號，不會影響主相關峰。

圖1 余弦型群時延對BPSK(10)信號的相關峰的影響Fig.1 Influence of cosine group delay on the correlation peak of BPSK(10)

雖然第4級(包括第4級)以上的正弦或余弦型群時延產生的回波與信號主相關峰的距離均大于兩倍碼片，不會對信號的主相關峰產生影響，但是多個余弦或正弦群時延的級聯仍然可能產生靠近主相關峰的回波。如第4和第5級余弦/正弦型群時延產生的回波相對于主相關峰的延遲分別為：

dτ4(k)=2kTc

(12)

dτ5(k)=2.5kTc

(13)

顯然，第4級余弦型/正弦型群時延產生的第k=-1時的回波與第5級余弦型/正弦型群時延產生的第k=1時的回波進行級聯會產生與主相關峰距離為Tc/2的回波，該回波會疊加到主相關峰上，導致主相關峰畸變。

盡管4級(包括第4級)以上余弦型群時延或正弦型群時延的級聯會產生接近主相關峰的回波，進而導致主相關峰畸變。但通常情況下，通道濾波器的群時延特性波動較為平緩，具有低通特性(如切比雪夫、巴特沃茲濾波器等)，即對其傅里葉分解后，i越大，群時延波動幅度ci和si越小，相應產生的回波信號幅度也越小，當i足夠大時，回波信號的幅度可忽略。例如，對于10.23 MHz碼率的擴頻信號，若通道濾波器帶寬取為20.46 MHz，群時延特性是波動幅度為150 ns的二次曲線。對該通道群時延在信號帶寬范圍內進行傅里葉分解后得到的各級余弦型群時延的波動幅度以及產生的第1對回波與主相關峰的幅度比如表1所示(通常情況下，根據貝塞爾函數的特性，|k|越大，幅度越小，因此這里僅考慮第1對回波的幅度)。由表1可知，第4級以后的余弦型群時延產生的回波信號幅度相對于主相關峰低37.7 dB以上，基本可以忽略。

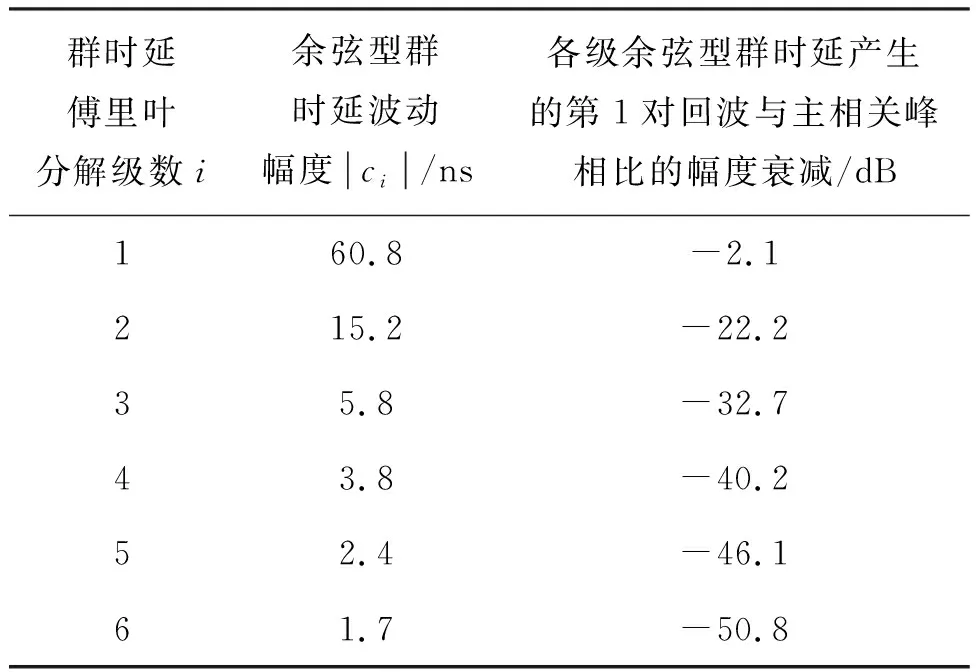
表1 帶寬為20.46 MHz，波動幅度為150 ns的二次群時延傅里葉分解后的前6級余弦型群時延的特性Tab.1 The first 6-lever cosine type group delay characteristics after Fourier decomposition of the parabola group delay with a bandwidth of 20.46 MHz and a fluctuation amplitude of 150 ns

上述例子采用了波動幅度為150 ns的拋物線群時延，這種群時延特性的通道濾波器已經非常惡劣了，大部分通道的群時延波動幅度要小于150 ns。因此通常情況下，對于二進制相移鍵控(Binary Phase Shift Keying, BPSK)信號，若濾波帶寬取為信號帶寬，可對其在信號帶寬內進行傅里葉分解，只需取前3級三角函數群時延即可等效表征該濾波器的群時延特性對信號相關峰的影響。

3 基于傅里葉級數模型的群時延測量方法

根據上述兩節的分析，三角函數群時延對于信號相關峰的影響是產生了一系列多徑信號，且三角函數頻率越高，多徑距離主瓣信號越遠，幅度也越低，影響也越小，高頻的三角函數群時延對信號相關峰的影響可忽略不計，大部分通道的群時延特性采用3級余弦型群時延和正弦型群時延即可等效表征，這樣只需要估計各級余弦型和正弦型群時延傅里葉分解系數ci和si即可完成通道等效群時延的估計。這里采用相關峰匹配的方法估計群時延的傅里葉分解系數，具體實現框圖如圖2所示，采用離線分析計算的方式預先計算好各種群時延傅里葉系數組合下的相關峰數據并存儲至本地，然后對經過通道的導航信號進行相關峰測量，利用測量得到的相關峰在本地相關峰數據庫中進行搜索并計算相關峰波形匹配度，波形匹配誤差最小時對應的系數ci、si即為傅里葉分解系數估計值，相應群時延估計值為：

(14)

圖2 基于相關峰匹配搜索的群時延測量框圖Fig.2 Block diagram of group delay measurement based on correlation peak matching search

3.1 離線預處理

采用離線分析計算的方式預先計算好各種群時延傅里葉系數組合下的相關峰數據并存儲至本地。

根據線性系統理論，經過相位響應為ψ′(f)的通道的擴頻信號相關峰可寫為：

(15)

其中，Gr(f)為擴頻信號功率譜。相應通道群時延特性為：

(16)

按一定步進遍歷一定幅度范圍內的傅里葉系數，并計算對應的群時延特性τ(f)與對應的相位響應ψ(f)，然后根據式(15)計算相關峰曲線。顯然，群時延的各級傅里葉分解系數遍歷步進越小，對任意群時延遍歷越精細，相關峰采樣間隔dt越小，相關峰曲線越精細，通過一階線性插值可獲取各相關峰采樣點之間的相關值。

3.2 群時延測量流程

對經過通道的導航信號進行相關峰測量，利用測量得到的相關峰在本地相關峰數據庫進行匹配搜索，搜索匹配誤差最小的相關峰，具體方法如下：

1)信號相關峰測量。令輸入的理想基帶信號時域波形為q(t)，其經過通道濾波器后的信號為q′(t)。首先采用經典的早遲環估計器估計q′(t)的時延τ0(早遲間隔取為d0)，對計算輸入信號的相關峰如式(17)所示：

(17)

由于實現資源受限，只能得到一定延遲間隔d0τ下的相關峰采樣值，相關峰采樣范圍為正負一個碼片。令擴頻碼片周期為T，延遲間隔d0τ=T/L，則相關峰采樣值如式(18)所示(已進行歸一化，相關峰最大值為1)：

(18)

2)相關峰匹配搜索。將測量得到的相關峰與本地存儲的精細相關峰數據進行匹配誤差計算，搜索匹配誤差最小的群時延傅里葉系數組合，該組系數即表征了群時延估計值。具體計算流程如下所示(對于任意一組群時延系數組合，假設其離線計算并存儲的相關峰為Rlocal(τ)(已進行歸一化)，測量得到的相關峰采樣值為R(k))：

①首先采用傳統早遲環估計器來估計某組本地相關峰的中心位置τ′0，其滿足(其中d0為早遲間隔)：

Rlocal(τ′0-d0/2)=Rlocal(τ′0+d0/2)

(19)

②對本地存儲的相關峰數據Rlocal(τ)進行采樣，各采樣點對應的延遲序列即為相關峰R(k)各采樣點對應的延遲量，采樣后得到的本地相關峰序列如式(20)所示：

R′local(k)=Rlocal(τ′0+kT/L-T)

(20)

③計算相關峰匹配誤差:

(21)

4 仿真驗證

采用碼率為10.23 MHz的擴頻碼信號對本文提出的群時延特性估計方法進行仿真驗證，濾波器帶寬為20.46 MHz。濾波器的群時延采用3階余弦型/正弦型群時延等效表示。

仿真驗證框圖如圖3所示，給定某通道濾波器H(f),首先采用本文所提出的基于傅里葉級數分解的群時延估計方法對該濾波器的群時延特性進行測量，得到各級傅里葉分解系數估計值c1,c2,c3，s1,s2,s3，具體步驟如下所示。

步驟1：計算各類傅里葉分解系數組合下的相關峰，并存儲至本地，各級傅里葉分解系數的遍歷步進取為0.1 ns，遍歷范圍取為-60～60 ns。

步驟2：計算給定傳輸函數H(f)通道的濾波器脈沖響應h(t)，生成理想基帶信號r(n)，并將其通過脈沖響應為h(t)的濾波器，輸出為rI(n)+jrQ(n)。

步驟3：對rI(n)+jrQ(n)進行相關峰測量，并在本地相關峰數據庫中進行匹配搜索。

步驟4：相關峰匹配誤差最小的系數組合即為群時延傅里葉級數的估計結果c1,c2,c3，s1,s2,s3。

隨后根據該估計結果修正原始傳輸函數H(f)，假設H(f)的群時延特性為τ(f)，則修正后的傳輸函數H′(f)的群時延響應如式(22)所示：

(22)

采用將理想基帶信號通過修正后的濾波器H′(f)，來計算精細相關峰以及不同相關間隔下的時延估計值，并與理想相關峰進行比對。

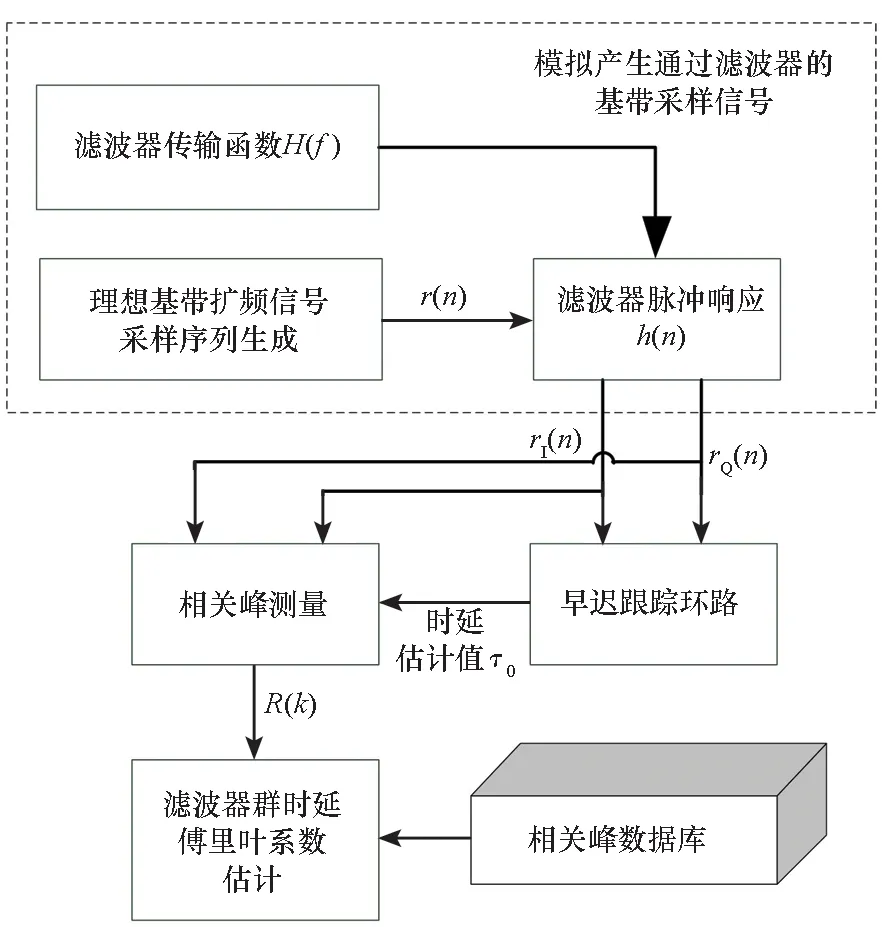
圖3 仿真驗證框圖Fig.3 Simulation and verification block diagram

仿真采用兩個濾波器：一個為給定系數的巴特沃茲濾波器，另一個為某導航接收機實際使用的中頻濾波器(其群時延特性采用矢量網絡分析儀測量得到)，兩個濾波器的群時延特性分別如圖4和圖5所示。

圖4 巴特沃茲仿真濾波器的群時延特性Fig.4 Group delay characteristics of simulation Butterworth filter

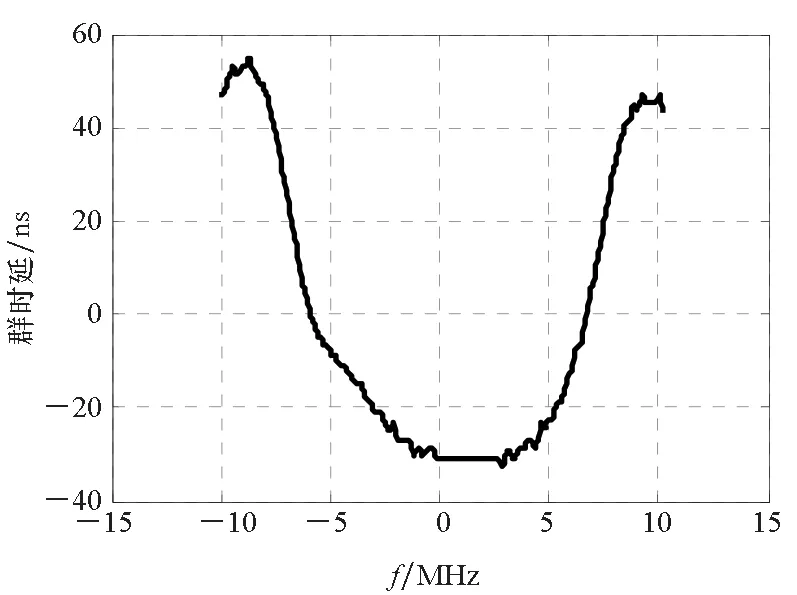
圖5 實際濾波器的群時延特性Fig.5 Group delay characteristics of actually measured filter

仿真結果如圖6～11所示，顯然理想信號經過上述兩個濾波器后均發生了不同程度的畸變(信號相關峰畸變，不同早遲間隔下的時延估計偏差互不相同)，這主要是由于群時延非理想導致。采用本文方法估計得到的群時延特性對濾波器進行群時延修正，顯然經過校準后，相關峰畸變得到修正，其與通過濾波器之前的信號相關峰高度吻合，差異幅度很小(主瓣范圍內差異約為主峰幅度的1/10 000量級)，同時不同早遲相關間隔的時延估計偏差在0.1 ns之內。仿真結果說明了本文所提出的群時延估計方法的正確性。

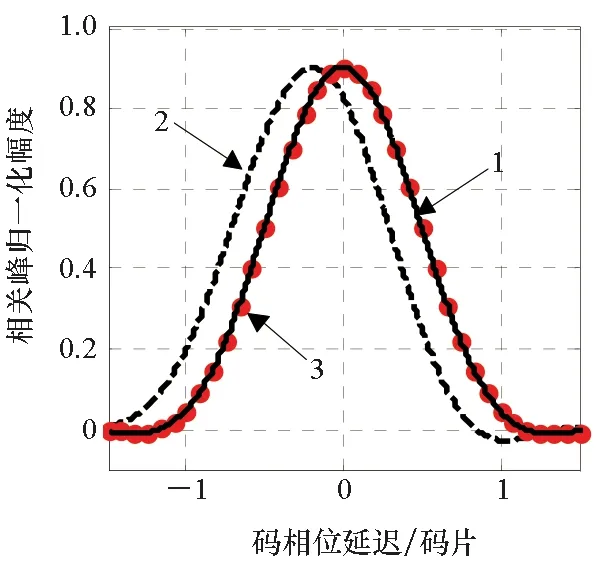
注：1—理想信號相關峰;2—經過濾波器后的相關峰; 3—采用群時延估計結果對濾波器校準后的相關峰。圖6 通過實際濾波器之后的信號相關峰、群時延校準后的相關峰與理想相關峰的對比Fig.6 Comparison of the correlation peaks after passing the actual filter, the correlation peak after group delay calibration and the ideal correlation peaks

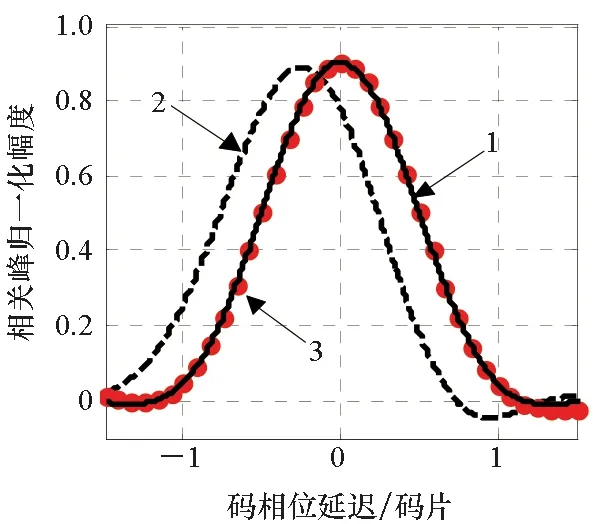
注：1—理想信號相關峰;2—經過濾波器后的相關峰; 3—采用群時延估計結果對濾波器校準后的相關峰。圖7 通過巴特沃茲濾波器之后的信號相關峰、群時延校準后的相關峰與理想相關峰的對比Fig.7 Comparison of the correlation peaks after passing the Butterworth filter, the correlation peak after group delay calibration and the ideal correlation peaks

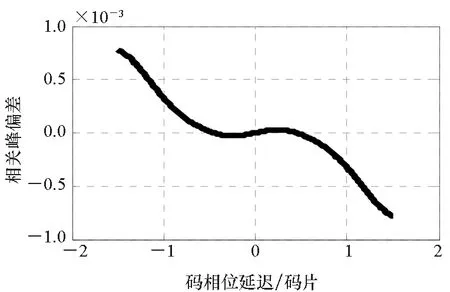
圖8 對通過實際濾波器的信號進行群時延校準后的信號相關峰與理想相關峰的偏差Fig.8 Bias between the ideal correlation peak and the correlation peak after group delay calibration of the signal passing through the actual filter

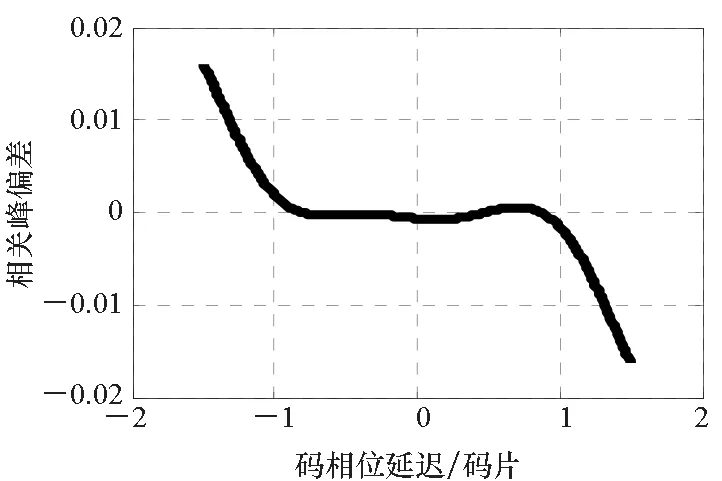
圖9 對通過巴特沃茲濾波器的信號進行群時延校準后的信號相關峰與理想相關峰偏差Fig.9 Bias between the ideal correlation peak and the correlation peak after group delay calibration of the signal passing through the Butterworth filter

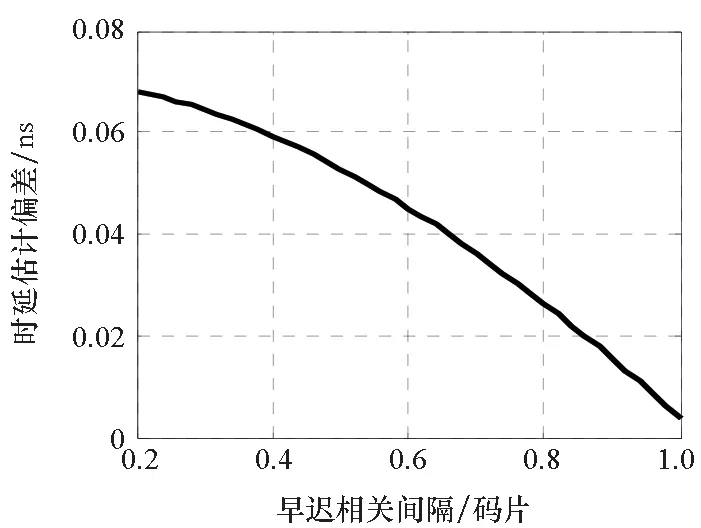
圖10 對通過實際濾波器信號進行群時延校準后，不同相關間隔下的時延估計偏差Fig.10 After the group delay calibration of the signal passing through the actual filter, the delay estimation bias under different correlation intervals

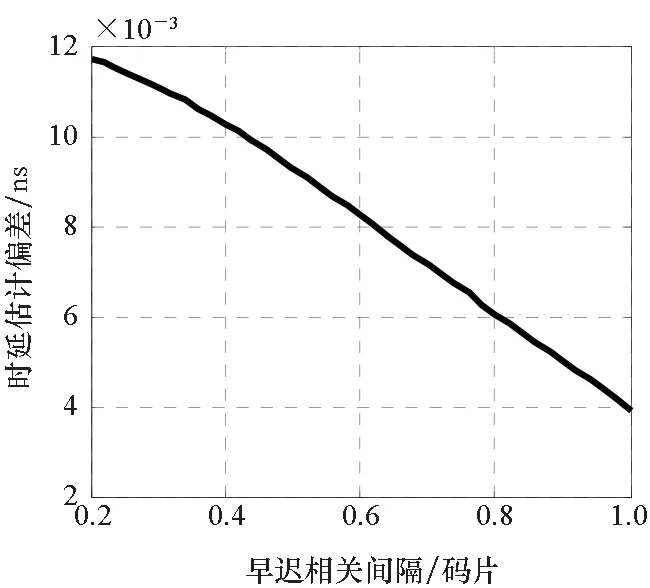
圖11 對通過巴特沃茲濾波器信號進行群時延校準后，不同相關間隔下的時延估計偏差Fig.11 After the group delay calibration of the signal passing through the Butterworth filter, the delay estimation bias under different correlation intervals

5 實測驗證

采用湖南衛導公司的NSS8000系列導航信號源與實際GNSS接收機對本文提出的群時延特性估計方法進行實測驗證，導航信號源播發單顆衛星高載噪比(大于50 dB-Hz)的B2a信號(盡可能消除互相關和測量噪聲的影響)，GNSS接收機B2a信號數字接收通道的線性相位有限長單位沖激響應(Finite Impulse Response, FIR)濾波器帶寬為25 MHz(接收機設計參數)。

具體的測試步驟如下所示。

步驟1：GNSS接收機對導航信號源發送過來的B2a信號進行接收處理，并測量相關峰(相關峰積累時長為1 s)，目前該接收機相關峰采集點數為32，間隔為1/16碼片。

步驟2：計算各類傅里葉分解系數組合下的相關峰(相關峰濾波帶寬為25 MHz，具體濾波器取為接收機B2a信號數字接收通道的線性相位FIR濾波器)，并存儲至本地，各級傅里葉分解系數的遍歷步進取為0.1 ns，遍歷范圍取為-60～60 ns。

步驟3：根據GNSS接收機測量得到的相關峰，按照本文方法在本地相關峰數據庫中進行匹配搜索，相關峰匹配誤差最小的系數組合即為群時延傅里葉級數的估計結果c1,c2,c3,s1,s2,s3，對應的通道群時延特性估計值如下(其中帶寬B為25 MHz)：

(23)

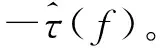
步驟5：群時延補償后，GNSS接收機再次進行相關峰測量，比較補償前后的相關峰測量結果，并計算補償前后不同早遲間隔下的測距偏差。

測試結果如圖12～14所示,其中圖12與圖13為GNSS接收機監控軟件所存儲相關峰測量數據的圖示，圖14為群時延校準前后不同相關間隔下的時延估計值，顯然，補償前信號相關峰存在畸變，不同早遲間隔下的時延估計偏差高達1.7 ns，經群時延估計補償后，相關峰畸變得到修正，不同早遲相關間隔的時延估計偏差在0.1 ns內。實測結果驗證了本文所提出的群時延估計方法的正確性。

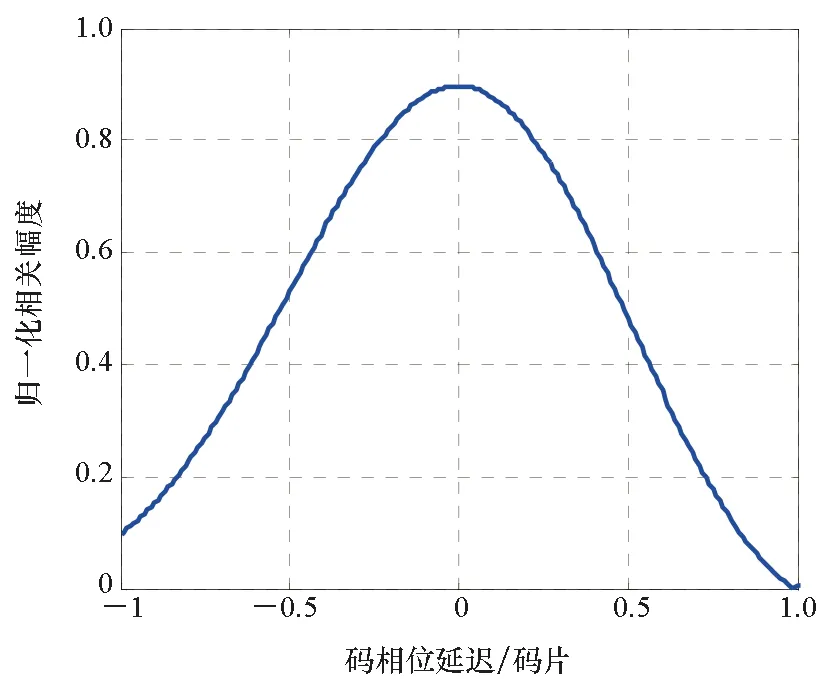
圖12 群時延補償之前的B2a信號相關峰Fig.12 B2a correlation peak before the group delay compensation

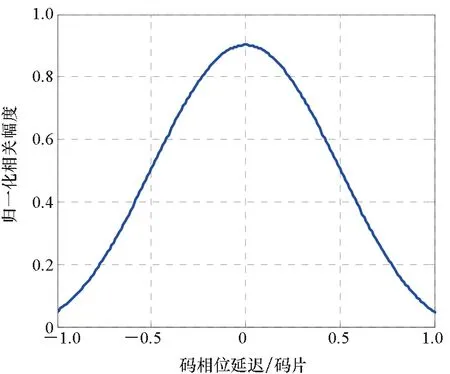
圖13 群時延補償后的B2a信號相關峰Fig.13 B2a correlation peak after the group delay compensation

圖14 群時延校準前后的不同相關間隔下的時延估計偏差Fig.14 Delay estimation bias in different intervals before and after calibration of group delay estimation

上述測量的是導航信號源和接收機級聯的群時延特性，導航信號源為標準設備，通常需給出其群時延特性，測量結果減去導航信號源的群時延特性即為GNSS接收機的群時延特性。

6 結論

本文通過理論推導分析了三角函數群時延對信號相關峰的影響，發現三角函數群時延對于信號相關峰的影響是產生了一系列多徑信號，且三角函數頻率越高，多徑距離主瓣信號越遠，幅度也越低，影響也越小，高頻的三角函數群時延對信號相關峰的影響可忽略不計，從而可將任意群時延特性分解為有限階數的三角函數群時延的疊加。基于此分析，通過測量信號相關峰，并與不同三角函數群時延組合下的相關峰進行匹配搜索即可估計群時延的三角函數分解級數，從而估計得到相關峰影響等效的群時延特性，仿真結果驗證了本文方法的準確性。相對于傳統基于矢量網絡分析儀的群時延測量方法，本文方法可實現軟件自動化測試，且不需要搭建額外復雜的硬件鏈路，測量效率更高，具有較強的工程應用價值。