行駛時(shí)間區(qū)間不確定的裝配線物料配送路徑規(guī)劃

張家驊 李愛(ài)平 劉雪梅

1.同濟(jì)大學(xué)機(jī)械與能源工程學(xué)院，上海，2018042.無(wú)錫工藝職業(yè)技術(shù)學(xué)院機(jī)電與信息工程學(xué)院，宜興，214206

0 引言

準(zhǔn)時(shí)化物料配送對(duì)企業(yè)降低生產(chǎn)成本、提高生產(chǎn)效率有重要意義。物料配送中的車輛路徑規(guī)劃問(wèn)題是一個(gè)重要決策問(wèn)題，近年來(lái)受到學(xué)者關(guān)注[1]。

文獻(xiàn)[2-4]對(duì)裝配線物料配送路徑規(guī)劃問(wèn)題進(jìn)行了研究，表明裝配線物料配送路徑規(guī)劃模型可以按帶時(shí)間窗的車輛路徑規(guī)劃問(wèn)題進(jìn)行建模與求解。吳倩云等[5]在此基礎(chǔ)上進(jìn)一步考慮了物料在配送車輛上的三維裝載約束。

上述研究考慮了配送車輛行駛時(shí)間確定的情況，但在變速箱裝配線等生產(chǎn)中，零件由配送員駕駛拖車同時(shí)對(duì)幾條裝配線進(jìn)行配送，該配送方式并不能精確控制拖車速度和行駛路線，車間中工作人員和貨物往來(lái)頻繁，更增加了配送車輛行駛時(shí)間的不確定性。不確定行駛時(shí)間增加了物料不能準(zhǔn)時(shí)送達(dá)工位的風(fēng)險(xiǎn)。KORYTKOWSKI等[6]研究發(fā)現(xiàn)物料能否準(zhǔn)時(shí)送達(dá)對(duì)裝配線生產(chǎn)性能有重要影響。TURNQUIST等[7]、VONOLFEN等[8]采用配送車輛行駛時(shí)間服從隨機(jī)概率的方法研究裝配線物料配送問(wèn)題。李晉航等[9]對(duì)裝配線中配送車輛運(yùn)輸時(shí)間等不確定信息進(jìn)行模糊化處理，建立了混流裝配線配送路徑的模糊機(jī)會(huì)約束規(guī)劃模型，并采用遺傳算法進(jìn)行了求解。然而實(shí)際生產(chǎn)中車輛不確定運(yùn)行時(shí)間的概率分布或模糊隸屬函數(shù)可能難以獲得，使上述方法的應(yīng)用受到了限制。

近年來(lái)，考慮不確定信息區(qū)間分布的魯棒優(yōu)化方法快速發(fā)展[10-11]，該方法不需要預(yù)知不確定信息的具體概率分布或模糊隸屬度函數(shù)，只需知道信息的區(qū)間范圍，這一方法在多個(gè)領(lǐng)域已經(jīng)被廣泛研究和應(yīng)用，包括應(yīng)用于經(jīng)典的車輛路徑規(guī)劃問(wèn)題。SUNGUR等[12]首次采用魯棒優(yōu)化方法研究了服務(wù)點(diǎn)需求不確定的車輛路徑問(wèn)題，建立了該問(wèn)題的混合整數(shù)規(guī)劃模型。BRAATEN等[13]針對(duì)魯棒車輛路徑優(yōu)化問(wèn)題的計(jì)算復(fù)雜性，提出了一種啟發(fā)式方法。HU等[14]針對(duì)車輛行駛時(shí)間和服務(wù)點(diǎn)需求不確定的魯棒車輛路徑問(wèn)題，引入路徑相關(guān)不確定參數(shù)，建立了優(yōu)化模型，并設(shè)計(jì)了一個(gè)兩階段智能求解算法。MUNARI等[15]研究了車輛行駛時(shí)間和服務(wù)點(diǎn)需求均不確定的魯棒車輛路徑問(wèn)題，設(shè)計(jì)了分支定價(jià)割平面求解算法。劉洋等[16]研究了養(yǎng)護(hù)時(shí)間不確定的養(yǎng)護(hù)車輛魯棒路徑規(guī)劃問(wèn)題。目前未見(jiàn)有關(guān)魯棒優(yōu)化方法在裝配線準(zhǔn)時(shí)化物料配送車輛路徑規(guī)劃中的應(yīng)用。

本文針對(duì)行駛時(shí)間不確定的裝配線物料配送車輛路徑規(guī)劃問(wèn)題，采用魯棒優(yōu)化方法，引入路徑相關(guān)不確定參數(shù)，建立行駛時(shí)間區(qū)間不確定的裝配線物料配送路徑規(guī)劃模型，并設(shè)計(jì)了求解該模型的混合遺傳算法。

1 問(wèn)題描述及模型建立

1.1 確定行駛時(shí)間的路徑規(guī)劃數(shù)學(xué)模型

裝配線物料配送路徑規(guī)劃問(wèn)題可以描述為：已知圖G=(V，A)，V={0，1，…，n}是工位節(jié)點(diǎn)集合，0表示物料配送中心，所有配送車輛從配送中心0出發(fā)，完成配送任務(wù)后返回配送中心，進(jìn)行下一次配送；A表示工位節(jié)點(diǎn)之間的弧。已知配送車輛數(shù)目為K，負(fù)責(zé)對(duì)n個(gè)工位進(jìn)行物料配送，每個(gè)工位只能由一輛車服務(wù)；每輛車的最大載重Q，車廂是三維矩形(長(zhǎng)L、寬W、高H)；第i工位的物料需求質(zhì)量為qi(i=1，2，…，n)，需ai個(gè)標(biāo)準(zhǔn)料箱來(lái)運(yùn)送物料，第a個(gè)料箱尺寸為lai、wai、hai(a=1，2,…，ai)；車輛需滿足最大載重量約束，每個(gè)工位所需物品放入同一輛車，料箱尺寸滿足車廂尺寸約束；車輛在第i工位的服務(wù)時(shí)間是ui；第i個(gè)工位的服務(wù)時(shí)間窗為[ei，bi]，如果車輛早于ei到達(dá)，則車輛進(jìn)行等待；晚于bi到達(dá)則被拒絕。

問(wèn)題目標(biāo)是在滿足約束的條件下尋找合理的車輛路徑，以達(dá)到車輛總行駛距離的最小化：

(1)

(2)

(3)

(4)

(5)

(6)

?k∈{1,2，…,K}p∈{1,2，…,n}

(7)

?i∈V{0}a∈{1,2，…,ai}

(8)

sik+ui+tij-M(1-xijk)≤sjk

(9)

ei≤sik≤bi

(10)

xijk∈{0,1}yik∈{0,1}

目標(biāo)函數(shù)式(1)表示最小化行駛距離，dij表示工位i到工位j的距離，xijk是決策變量，xijk=1表示車輛k從工位i駛往j。約束式(2)～式(5)分別表示有K輛車離開(kāi)配送中心、每個(gè)工位正好被訪問(wèn)一次，以及進(jìn)入和離開(kāi)每個(gè)工位組只有一輛車，式中yik是輔助決策變量，yik=1表示工位i采用車輛k配送。約束式(6)保證車輛行駛線路的連通性。式(7)是料箱在車廂內(nèi)的尺寸約束，xai，yai，zai表示的是工位i所需料箱a在車廂中的左后下角的坐標(biāo)，坐標(biāo)系原點(diǎn)位于車廂內(nèi)側(cè)左后下角頂點(diǎn)，即首個(gè)料箱左后下角擺放的位置頂點(diǎn)。式(8)是每輛車的裝載容量限制。約束式(9)要求由同輛車配送的兩個(gè)工位，只有配送完前一個(gè)工位，車輛行駛到后一個(gè)工位后，才能執(zhí)行配送，sik為車輛k在工位i服務(wù)開(kāi)始時(shí)間，ui為車輛在工位i的服務(wù)時(shí)間，tij為車輛從工位i到工位j的行駛時(shí)間，此處該時(shí)間是確定的，M是一個(gè)大的正數(shù)。式(10)是時(shí)間窗約束。

1.2 不確定行駛時(shí)間的路徑規(guī)劃模型

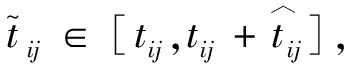
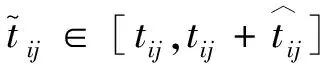
θ=0，Λk=0，表明車輛k路徑中任一弧上的行駛時(shí)間均不發(fā)生波動(dòng)；θ=1，Λk=|Ak|，表明車輛k所在路徑中的所有弧的行駛時(shí)間都發(fā)生波動(dòng)。根據(jù)魯棒優(yōu)化原理[17]，當(dāng)每條路徑中最多|Ak|段弧發(fā)生波動(dòng)時(shí)，解仍然是可行的，說(shuō)明該解是魯棒的。

定義si,k,γk是第k條路徑有γk條弧上的行駛時(shí)間發(fā)生波動(dòng)的情況下車輛k在工位i的最差服務(wù)開(kāi)始時(shí)間，該值可以通過(guò)下式計(jì)算得到：

(11)

其中，當(dāng)i是物料中心即i=0時(shí)，車輛服務(wù)開(kāi)始時(shí)間不受不確定性的影響；當(dāng)i是物料需求工位時(shí)，分兩種情況：①如果γk=0則表示弧上沒(méi)有行駛時(shí)間發(fā)生波動(dòng)，車輛最差服務(wù)開(kāi)始時(shí)間等于行駛時(shí)間確定情況下的值；②如果γk≠0則車輛在工位i的最差服務(wù)開(kāi)始時(shí)間與該工位的時(shí)間窗的下限、上一個(gè)工位已經(jīng)達(dá)到最差服務(wù)開(kāi)始時(shí)間或本工位達(dá)到最差服務(wù)開(kāi)始時(shí)間相關(guān)。

按照上述分析，不確定行駛時(shí)間的路徑規(guī)劃模型只需要在上一節(jié)確定行駛時(shí)間的模型基礎(chǔ)上，根據(jù)式(11)對(duì)式(9)和式(10)修改為

si,k,γk+ui+tij-M(1-xijk)≤sj,k,γk

(12)

?i,j∈Vk=1,2，…,Kγk=0,1，…,Λk

(13)

?i,j∈Vk=1,2，…,Kγk=1,2，…,Λk

ei≤si,k,γk≤bi

(14)

其余公式均保留不變。

2 混合遺傳算法

傳統(tǒng)的車輛路徑問(wèn)題被證明是NP-hard問(wèn)題，本問(wèn)題在傳統(tǒng)車輛路徑問(wèn)題上，還需考慮時(shí)間窗，三維裝載和不確定行駛時(shí)間約束，求解更加困難。智能算法是求解該類問(wèn)題的主要方法，其中遺傳算法被認(rèn)為是最有效的求解方法之一，但單純的遺傳算法存在早熟收斂、易陷入局部最優(yōu)的缺點(diǎn)[18]。已有研究表明，模仿鳥(niǎo)類飛行行為的萊維飛行可以擴(kuò)大算法的搜索范圍，幫助算法及時(shí)跳出局部最優(yōu)[19-20]。傳統(tǒng)的萊維飛行不能直接應(yīng)用于離散優(yōu)化問(wèn)題，文獻(xiàn)[21]針對(duì)旅行商問(wèn)題提出一種離散萊維飛行，通過(guò)控制萊維飛行的步長(zhǎng)來(lái)實(shí)現(xiàn)不同弧之間的局部搜索。本文針對(duì)所研究的問(wèn)題，在上述文獻(xiàn)的基礎(chǔ)上，設(shè)計(jì)了另一種離散萊維飛行來(lái)增強(qiáng)算法的搜索能力。

圖1是算法流程圖，首先利用遺傳算法快速找到可行解，然后通過(guò)離散萊維飛行對(duì)可行解進(jìn)行局部搜索，改善解的質(zhì)量。

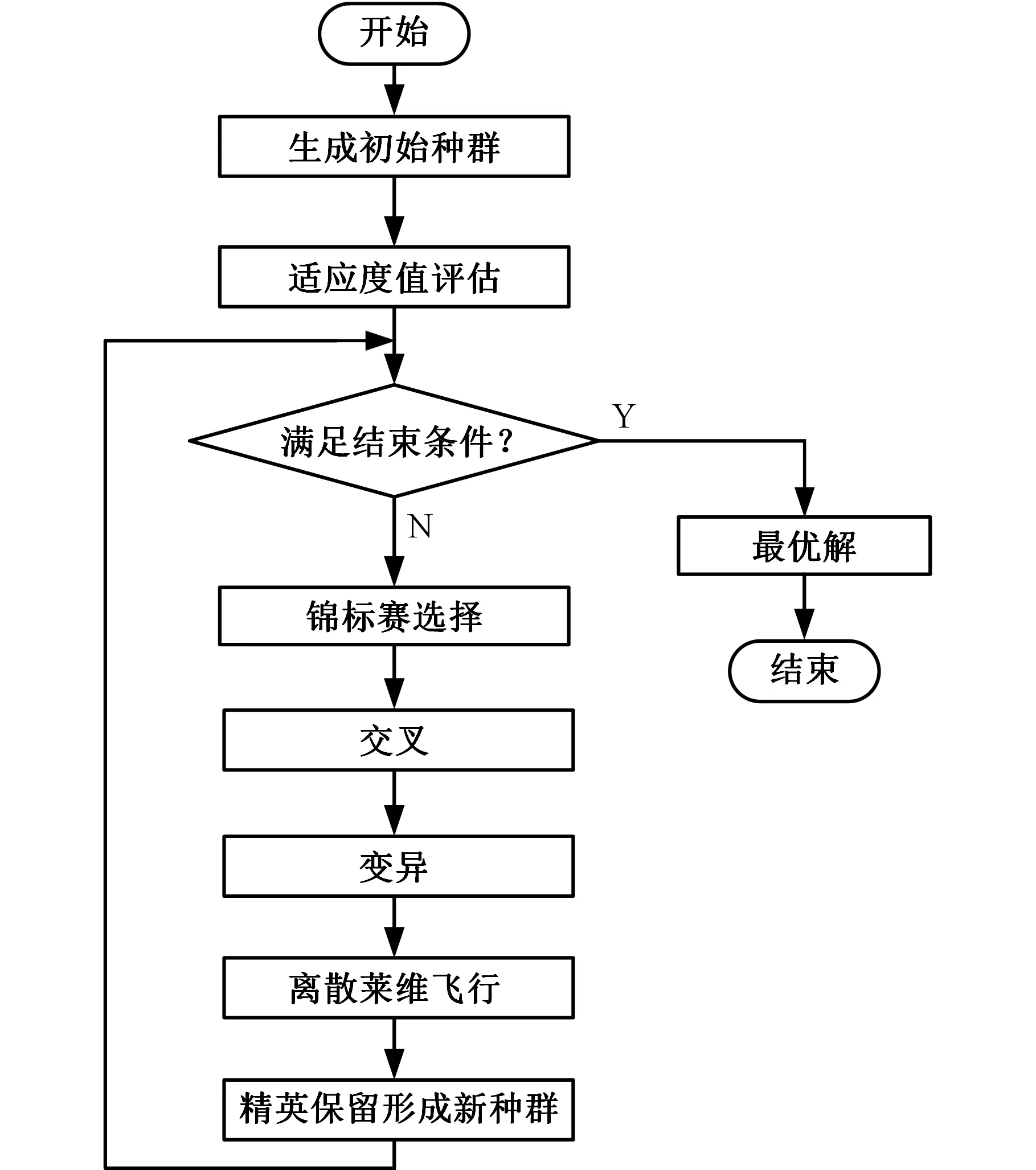
圖1 算法流程圖

2.1 初始種群與適應(yīng)度值評(píng)估

染色體采用自然數(shù)編碼方式，自然數(shù)1,2，…,n代表工位數(shù)，0表示配送中心，車輛數(shù)K已知，可表示長(zhǎng)度為n+K+1的向量(0，i11，i12，…，i1s，0,i21，i22，…，i2t，…，0，iK1，iK2，…,iKw，0)，其中ikj表示第k輛車服務(wù)的第j個(gè)工位的工位號(hào)。圖2所示染色體表示2輛車對(duì)7個(gè)工位進(jìn)行物料配送。為增加種群的多樣性，按種群規(guī)模，采取隨機(jī)法生成初始種群。

圖2 染色體示例

根據(jù)染色體的基因值，可直接解碼得到車輛的行駛路徑。由圖2所示染色體可得第一輛車的行駛路徑是0-1-3-7-0，第二輛車的路徑是0-2-4-5-6-0。根據(jù)車輛路徑，可計(jì)算出第k輛車的行駛距離fdk，第k輛車的載重fqk。按照式(11)可得在不同θ下每輛車經(jīng)過(guò)工位i的最差可能服務(wù)開(kāi)始時(shí)間si,k,Λk。

染色體中每輛車訪問(wèn)過(guò)的工位可以進(jìn)一步解碼為(rai，xai，yai，zai，lai，wai，hai)，rai是工位i中料箱a的疊放順序。按照料箱放置從下到上、從前到后、從左到右的規(guī)劃，可以得到每輛車料箱的最終xk、yk、zk。

由以上得到的結(jié)果，可以計(jì)算出適應(yīng)度值：

其中，M用來(lái)對(duì)違反約束進(jìn)行懲罰。

2.2 遺傳算子

輪盤(pán)賭選擇就是按照適應(yīng)度值計(jì)算染色體在子代中出現(xiàn)的概率，該方法適用于求解最大化問(wèn)題，如果求解最小化問(wèn)題，則需要對(duì)適應(yīng)度值函數(shù)進(jìn)行轉(zhuǎn)化，而采用錦標(biāo)賽選擇可以避免此類問(wèn)題并獲得更好性能[22]。由于本文研究最小化問(wèn)題，故采用錦標(biāo)賽選擇，每次從種群中隨機(jī)抽取兩個(gè)染色體，選擇其中最好的一個(gè)進(jìn)入子代種群。交叉算子采取類PMX交叉過(guò)程，若得到的子個(gè)體不合法，則通過(guò)調(diào)整0代碼的位置來(lái)使染色體可行[9]。變異算子采用交換兩點(diǎn)基因值策略[23]。

2.3 離散萊維飛行

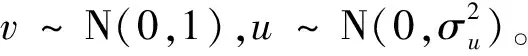
式中，β∈[1, 2]，β一般取值為1.5；Γ(·)表示伽馬函數(shù)。

文獻(xiàn)[20]針對(duì)旅行商問(wèn)題提出了一種離散萊維飛行，通過(guò)λ控制鄰域搜索，實(shí)現(xiàn)解的更新。本文據(jù)此設(shè)置萊維飛行策略如下：如果λ≤1，則隨機(jī)選擇一條路徑，對(duì)路徑內(nèi)的任一段基因序列進(jìn)行逆轉(zhuǎn)，實(shí)現(xiàn)短距離的萊維飛行；如果λ>1，則隨機(jī)選擇兩條路徑，對(duì)其進(jìn)行2-opt*交換[24]，實(shí)現(xiàn)在路徑間的鄰域搜索。圖3和圖4是離散萊維飛行的兩種不同方式的示例。

圖3 路徑內(nèi)飛行

圖4 路徑間飛行

最后，將離散萊維飛行后的種群與原種群進(jìn)行比較，將目標(biāo)值較小的染色體保留形成新的種群，進(jìn)行下一次進(jìn)化，直到滿足迭代要求。

3 案例分析

3.1 算法對(duì)比

文獻(xiàn)[3]針對(duì)16個(gè)工位、6輛配送車輛的總裝線物料配送路徑規(guī)劃問(wèn)題提出了一種遺傳算法進(jìn)行求解，具體數(shù)據(jù)見(jiàn)文獻(xiàn)[25]。針對(duì)文獻(xiàn)[3]的問(wèn)題，采用其模型和算法參數(shù)，在MATLAB平臺(tái)上使用本文所提算法對(duì)該案例進(jìn)行了計(jì)算，結(jié)果如表1所示。從表1中可得，本文的算法能夠得到比原算法更優(yōu)的結(jié)果，這主要是由于采用離散萊維飛行后擴(kuò)大了算法的搜索空間，說(shuō)明本文提出的算法改進(jìn)策略有效。

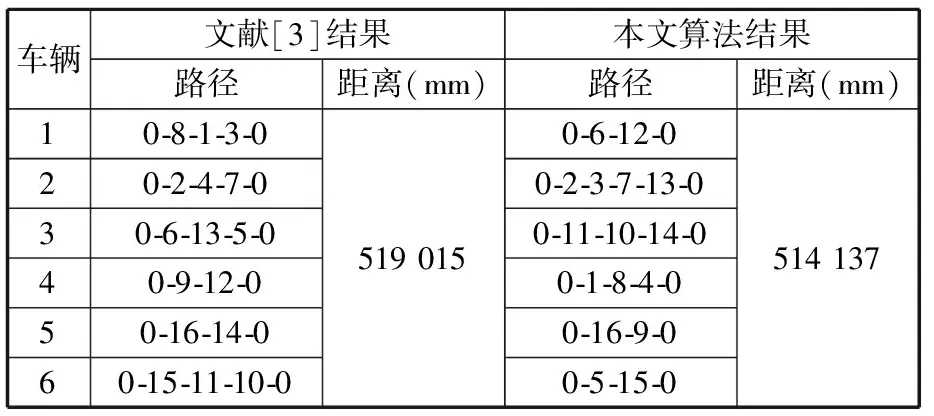
表1 不同算法結(jié)果的對(duì)比

3.2 實(shí)例描述

某變速器裝配車間由變速器總成裝配線、制動(dòng)器分裝線、輸入軸和離合器分裝線、后蓋分裝線和主箱體分裝線組成，車間共有9個(gè)物料需求工位。物料配送由2輛相同的拖車執(zhí)行，拖車參數(shù)見(jiàn)表2。表3所示是物料使用的4種不同規(guī)格的料箱尺寸。表4所示是工位的物料需求量和需求時(shí)間窗。表5所示是工位間的距離與行駛時(shí)間，其中行駛時(shí)間用區(qū)間數(shù)表示。各物料需求工位的服務(wù)時(shí)間是1 min。

表2 拖車規(guī)格參數(shù)

表3 標(biāo)準(zhǔn)料箱規(guī)格參數(shù)

表4 各工位貨物需求量和時(shí)間窗

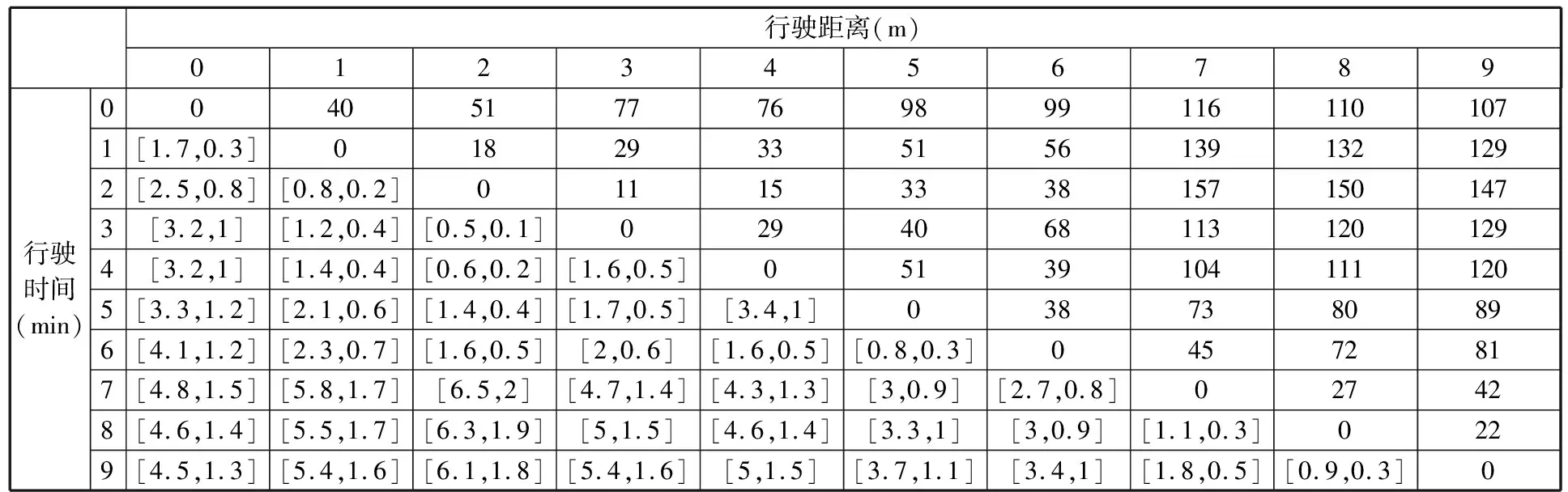
表5 各工位間行駛距離和行駛時(shí)間

算法參數(shù)設(shè)置如下：種群規(guī)模100，交叉概率0.8，變異概率0.2，終止迭代次數(shù)100。

3.3 實(shí)例結(jié)果分析

為了分析θ對(duì)結(jié)果的影響，計(jì)算θ為0、0.1、0.5、1時(shí)的結(jié)果。θ=0表示結(jié)果不考慮不確定的影響，θ為0.1、0.5、1分別代表結(jié)果考慮低、中、高3種不確定程度。圖5是不同θ下的目標(biāo)值收斂曲線，表6所示是具體路徑方案和目標(biāo)值。從圖5中可得，θ值越大，目標(biāo)值收斂速度越快，這是由于隨著考慮不確定程度增加，可滿足約束條件的解越少，使問(wèn)題可行解對(duì)應(yīng)染色體空間可能性變小，種群內(nèi)的解差異性增大，利于算法更早達(dá)到全局最優(yōu)解。

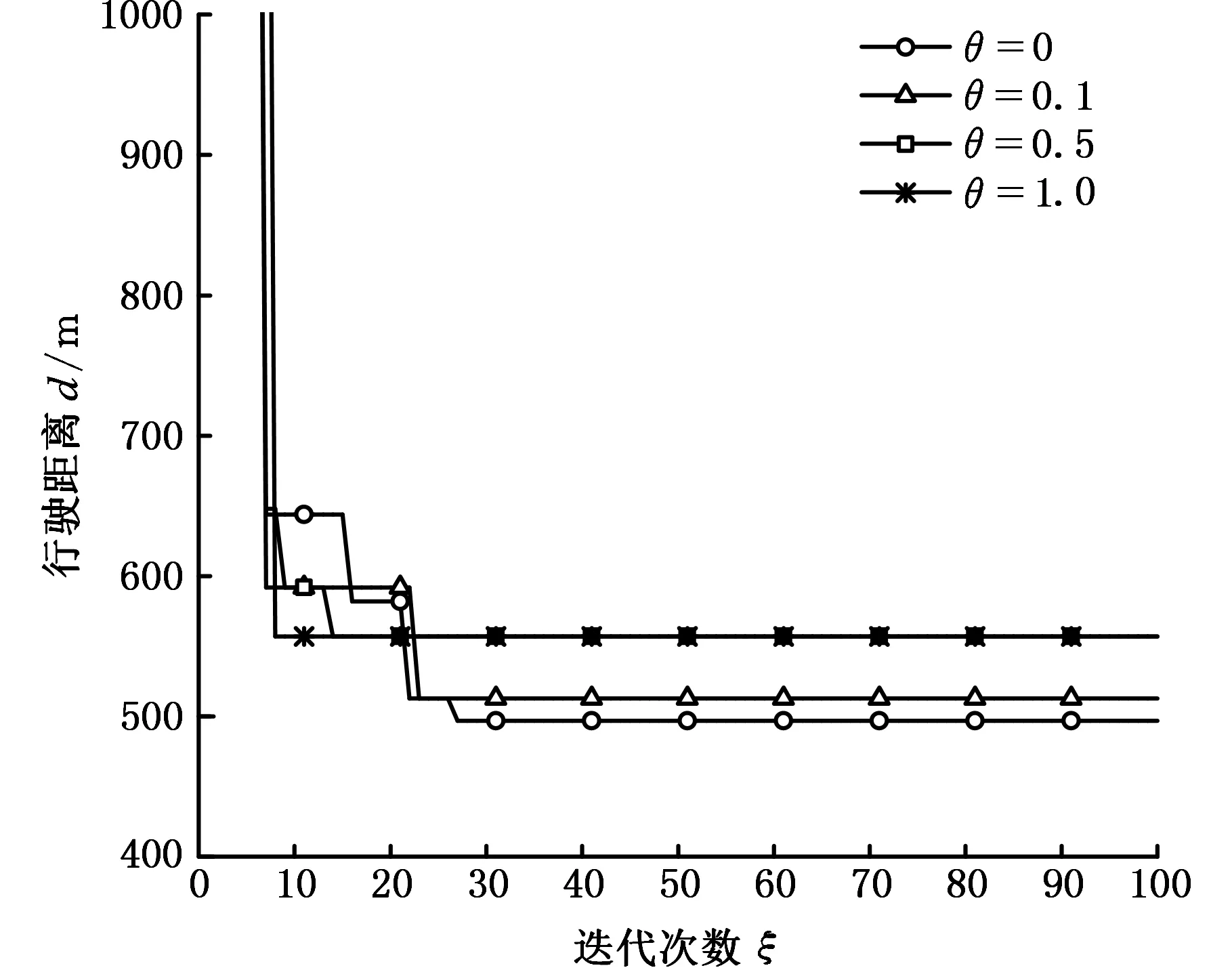
圖5 不同θ下的行駛距離的對(duì)比

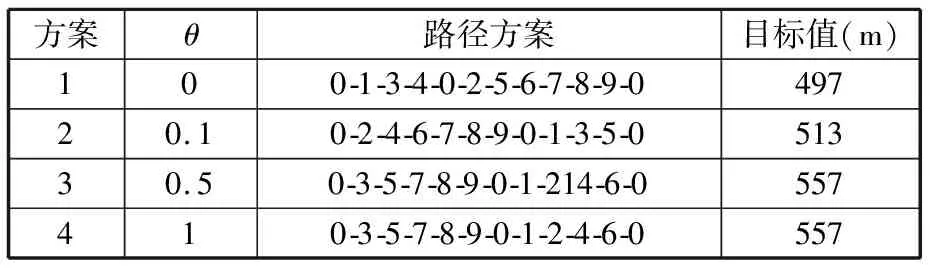
表6 不同θ下的具體結(jié)果

從圖5和表6中可得，θ對(duì)車輛行駛距離也有影響。θ從0增加到0.5，目標(biāo)值不斷增大；θ為0.5和1時(shí)，目標(biāo)值保持不變。這是因?yàn)闉榱说挚共淮_定的行駛時(shí)間，需要調(diào)整行駛路線，增加行駛距離；但當(dāng)考慮了足夠的不確定程度時(shí)，行駛路線不再發(fā)生變化。

以θ為0和0.1的結(jié)果分析解如何抵抗不確定行駛時(shí)間的影響。圖6所示是θ=0時(shí)配送車輛的路徑方案，工位號(hào)上方的是各個(gè)工位的時(shí)間窗，下方是車輛到達(dá)工位的服務(wù)開(kāi)始時(shí)間。得到的路徑方案保證了服務(wù)開(kāi)始時(shí)間在物料配送的時(shí)間窗內(nèi)，但這個(gè)方案不考慮不確定行駛時(shí)間。如果行駛時(shí)間發(fā)生波動(dòng)，例如第一條路徑中工位3-工位4，見(jiàn)表5，則存在可能的波動(dòng)時(shí)間0.5 min，如果發(fā)生波動(dòng)，那么實(shí)際最差的服務(wù)開(kāi)始時(shí)間是18.6+0.5=19.1 min，該時(shí)間超過(guò)了工位4允許的時(shí)間窗上限，導(dǎo)致方案不可行。

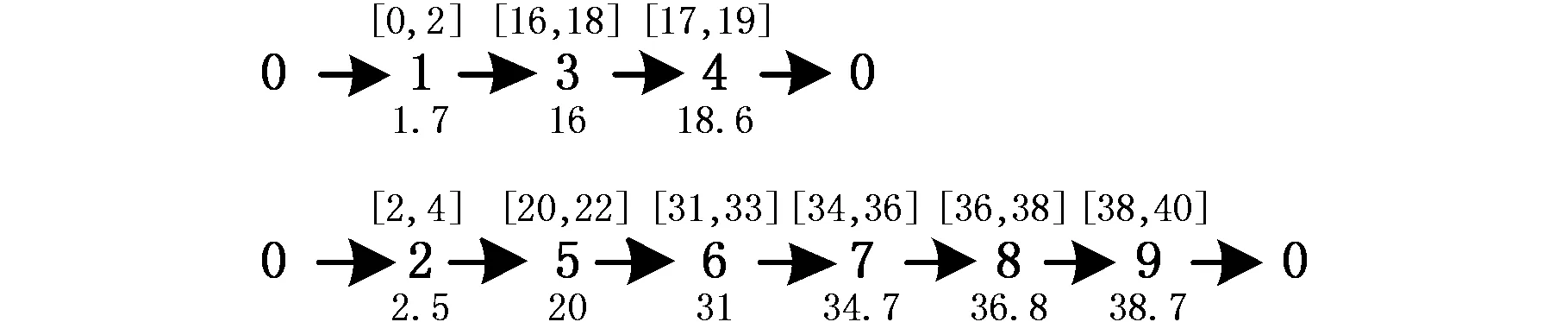
圖6 θ=0時(shí)車輛服務(wù)開(kāi)始時(shí)間(min)

圖7所示是θ=0.1時(shí)的路徑方案，工位的服務(wù)開(kāi)始時(shí)間下方的數(shù)字是考慮如果路徑中發(fā)生θ=0.1不確定情況時(shí)每個(gè)工位最差服務(wù)開(kāi)始時(shí)間。與θ=0路徑的不同之處在于，該方案將訪問(wèn)順序4和5進(jìn)行了互換。由圖7可以看到，即使路徑中發(fā)生θ=0.1的行駛時(shí)間波動(dòng)，車輛的服務(wù)開(kāi)始時(shí)間依然滿足時(shí)間窗要求，有效抵抗了不確定行駛時(shí)間的影響。

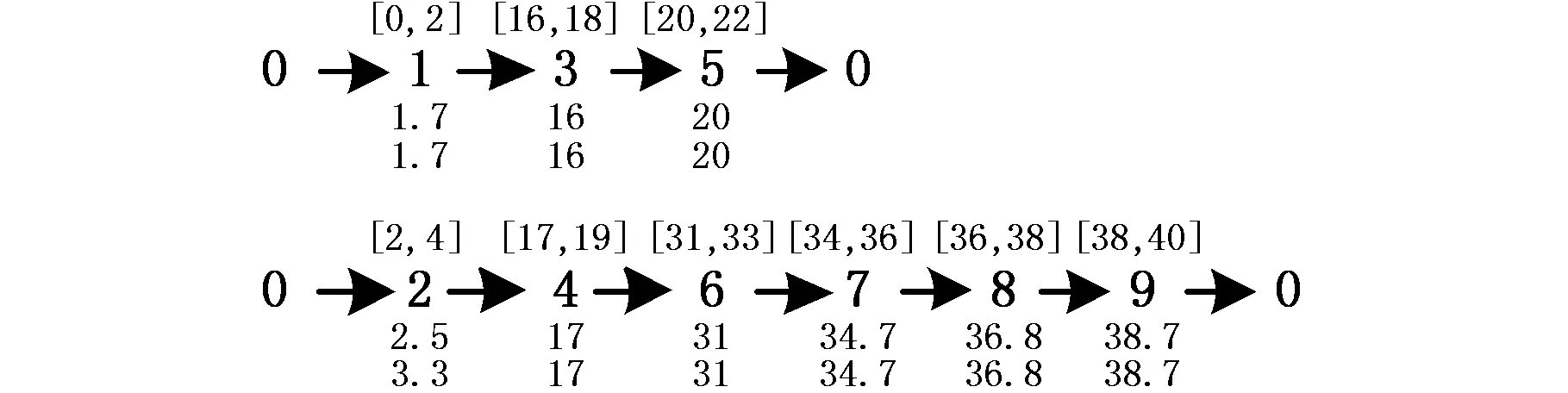
圖7 θ=0.1時(shí)車輛服務(wù)開(kāi)始時(shí)間(min)

為了進(jìn)一步獲得各個(gè)路徑方案抵抗不確定行駛時(shí)間的能力，采用蒙特卡羅模擬法[26]對(duì)結(jié)果進(jìn)行分析。在給定θ下，蒙特卡羅模擬法評(píng)價(jià)解抵抗不確定行駛時(shí)間的過(guò)程如下：①輸入路徑方案；②產(chǎn)生N個(gè)θ條件下的不確定行駛時(shí)間場(chǎng)景(N=10 000)，每個(gè)場(chǎng)景中的不確定行駛路徑的路段數(shù)按照θ隨機(jī)選擇，路段內(nèi)不確定行駛時(shí)間在各自區(qū)間內(nèi)按均勻分布產(chǎn)生；③對(duì)解在每個(gè)場(chǎng)景中的可行性進(jìn)行分析；④對(duì)解可行性的結(jié)果進(jìn)行統(tǒng)計(jì)，輸出解在當(dāng)前θ下的可行概率。

通過(guò)調(diào)整θ可以觀察不同方案抵抗不同不確定程度的能力，結(jié)果如表7所示，方案4結(jié)果同方案3。從表7中可看到，方案1抵抗不確定性的能力隨著路徑中的不確定程度增加而降低，這是因?yàn)樵摲桨竿耆珱](méi)有考慮行駛時(shí)間不確定的影響；方案2與要求一致，能夠完全抵抗θ=0.1的不確定性，隨著不確定性程度的增加，該方案的抵抗能力依然很強(qiáng)；方案3的結(jié)果則能夠完全抵抗住所有不確定的情況。

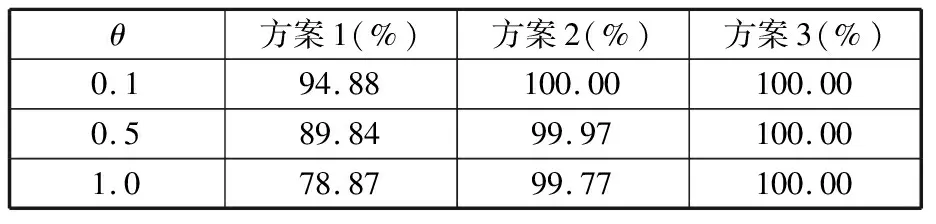
表7 各方案抵抗不同不確定程度的可行概率

由上文分析可知，為了抵抗不確定性，需要調(diào)整車輛運(yùn)行路徑，這會(huì)導(dǎo)致車輛行駛距離增加，因此決策者要根據(jù)實(shí)際情況，綜合運(yùn)行成本來(lái)選擇最佳車輛路徑方案。從本案例分析可以得到，方案2能夠以較短的行駛距離，使行駛路徑基本不受不確定行駛時(shí)間的影響，保證裝配線的穩(wěn)定運(yùn)行。

4 結(jié)論

(1)為了考慮裝配線物料配送中車輛行駛時(shí)間區(qū)間不確定對(duì)路徑規(guī)劃的影響，本文采用魯棒優(yōu)化方法，引入路徑相關(guān)不確定參數(shù)，建立了魯棒路徑規(guī)劃模型。

(2)提出了一種求解該模型的混合遺傳算法，在算法中，使用錦標(biāo)賽選擇算子，避免適應(yīng)度值的轉(zhuǎn)換；使用離散萊維飛行來(lái)提高算法的搜索性能。計(jì)算案例表明該混合算法比傳統(tǒng)遺傳算法能得到更好的解。

(3)求解結(jié)果與路徑相關(guān)不確定參數(shù)有關(guān)，決策者需要根據(jù)實(shí)際情況，綜合運(yùn)行成本來(lái)選擇最佳路徑方案。