原來它們是“一伙”的

孫天瀚

習題呈現（蘇科版數學八年級上冊第36頁第11題）：

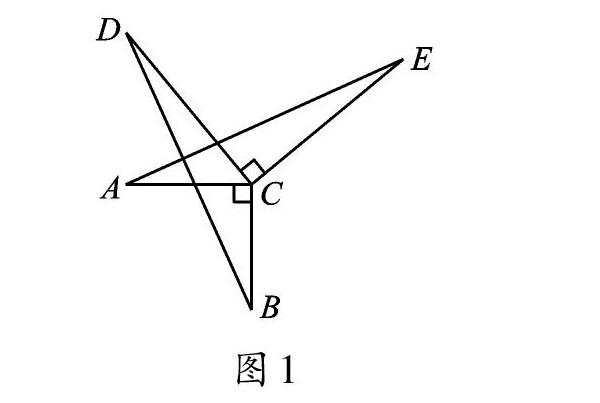
如圖1，AC⊥BC，DC⊥EC，AC=BC，DC=EC。圖中AE、BD有怎樣的數量關系和位置關系？試證明你的結論。

我發(fā)現△ACE繞點C逆時針旋轉可與△BCD重合。于是，我的解題思路是：證明△ACE≌△BCD，依據是“SAS”，進而發(fā)現AE=BD，AE⊥BD。

在解決這個問題的過程中，要先通過∠DCE=∠ACB=90°，證得∠ACE=∠DCB。我仔細琢磨，幾番思考：題中給出了“AC⊥BC，DC⊥EC”，為什么要強調“垂直”呢？

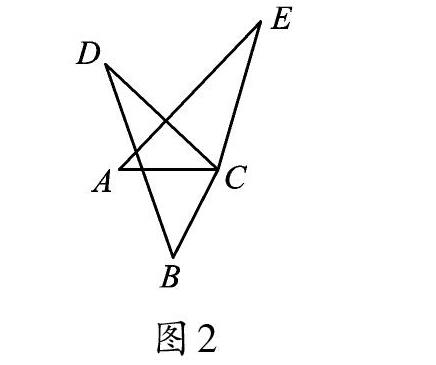
我嘗試將“AC⊥BC，DC⊥EC”改為“∠DCE=∠ACB=60°”，如圖2，同樣也可證得∠ACE=∠DCB，進而證明△ACE≌△BCD，這樣，結論AE=BD仍然成立。但是AE⊥BD不成立，這時可以求出AE與BD相交成的銳角為60°。

如果將“AC⊥BC，DC⊥EC”改為“∠DCE=∠ACB=45°”，如圖3，同樣也可證明△ACE≌△BCD，結論AE=BD仍然成立，AE⊥BD不成立，但可以求出AE與BD相交成的銳角為45°。

于是，我就想到了更一般的情況，將“AC⊥BC，DC⊥EC”改為“∠DCE=∠ACB=α（0°<α<90°）”，如圖4，類似地證明△ACE≌△BCD，發(fā)現AE=BD，AE與BD相交成的銳角為α。如果將“AC⊥BC，DC⊥EC”改為“∠DCE=∠ACB=α（90°<α<180°）”，如圖5，同樣可證得AE=BD，AE與BD相交成的銳角為180°-α。

在學習中，我發(fā)現類似這樣的問題會經常遇到，而且它們都是“一伙”的。因為不論是條件改變，還是圖形變化，都可以用同樣的方法去解決。

教師點評

小作者善于觀察、比較、思考，通過解題后的反思，從特殊到一般，在圖形的變化中，發(fā)現了問題的本質，自主探索發(fā)現了一類問題的解題策略。原來它們是“一伙”的，是一個了不起的發(fā)現。

（指導教師：單維娟）