Gabor與PCA融合算法的人臉識別技術*

陳秀端

（漳州職業技術學院機械工程學院，福建 漳州 363000）

0 引言

隨著社會信息化的飛速發展，人類越來越重視信息安全。在眾多的生物識別技術中，人臉識別技術應用廣泛，易被受檢者接受。

近年來，人臉識別技術飛速發展[1]，Turk與Pentland提出PCA（principal component analysis），用于提取人臉圖像的主要特征，是早期人臉識別技術的基礎[2-5]。Gabor算法進行特征提取之后數據量太大，不利于復雜圖像的信息提取[6]。本課題通過對Gabor小波變換算法與PCA主成分分析算法的分析，先用Gabor分解圖像提取特征再濾波，再用PCA降維，最后進行實驗設計和驗證。結果表明，相比于傳統的PCA算法，Gabor與PCA融合算法的人臉識別技術，識別率提高了。

1 原理介紹

1.1 Gabor小波變換介紹

小波是指幅值為0，具有一定長度的極小區域的波形。“小”顧名思義是指波形的衰減性，“波”形象地描述了波形的波動性[7]。由于傅立葉變換的缺陷是不能隨頻率變換的，而Gabor提供的這種變換窗口可以隨頻率而改變時域-頻域。運用窗函數g（t-τ）乘以信號函數f（t），實現了τ周邊的開窗。

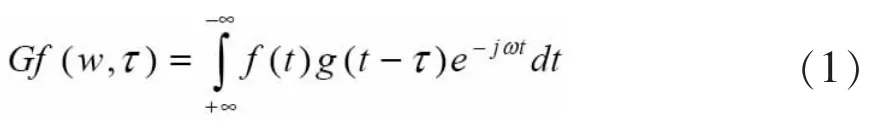
從式（1）可以看出，Gabor測量的是在τ附近的小區域內的頻率，是ω的正弦函數分量的幅度。窗函數g（t-τ）是高斯函數，經過傅立葉處理后仍是高斯函數，這就使得在小窗口內，在時域-頻域上，傅立葉變換具有局部化的作用，如果窗口函數ga（t）這樣定義：

這樣，小窗口寬度就由參數a決定，把式（2）代入

式（1）進行傅立葉處理再積分，得出它的頻譜公式：

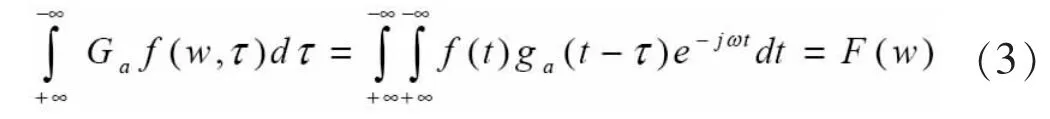
可見，通過傅立葉變換分解了f（τ）的頻譜F（w），從而得到了信號的局部信息[8]。如果τ在時間軸上平行移動，可得出傅立葉計算公式：

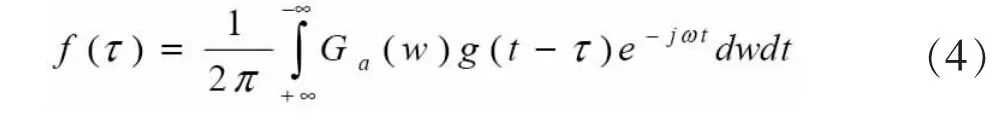
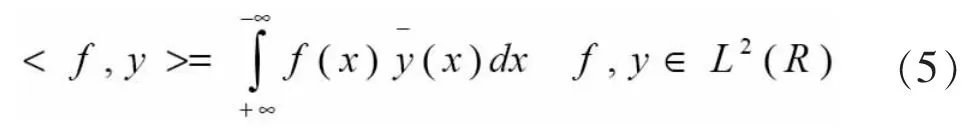
當f（x）=y（x）時：

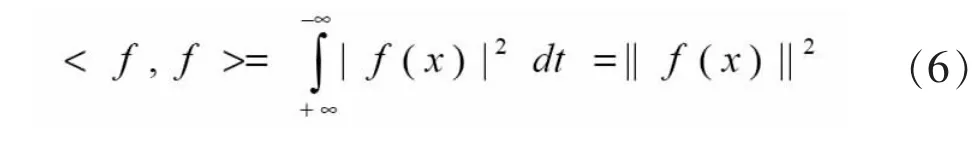
│f（x）│是f（x）的函數。用角頻率的變化量r替代時間的變化量t，同時用頻域的窗口函數G（r-ω）替代時域的窗口函數g（t-τ），可得頻域ω周邊的局部信息：

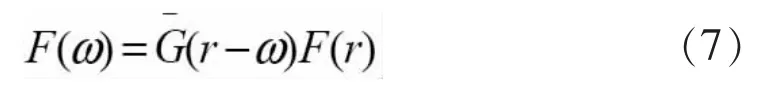
所以，Gabor小波變換的基本原理是：只要選取的小窗口在時域-頻域的局部性質良好，就能夠運用Gabor變換原理準確無誤提取到時域-頻域信號F（t）的特征信息[9]。

1.2 PCA主成分分析算法介紹

PCA是以K-L正交變換為基礎的算法，再運用奇異值分解計算法壓縮數據，提取人臉圖像特征信息[10-11]。下面介紹K-L正交變換與奇異值分解算法。K-L正交變換是生物識別領域中最常用、最熱門的算法，由Kirby等科學家提出，研究上常用K-L處理過的識別圖信息替代原來識別圖的信息。多數實驗證明，K-L是一種壓縮圖像信息的最佳處理方式，依照統計學，K-L正交變換可以找到最小的信息。

設被識別圖像是二維灰度圖f（x,y），若用M維向量表示，則圖像訓練集就可以看成是N維的隨機變量。Xi表示訓練集中第i個樣本的圖像矢量，所以訓練集中的樣本總數為M，則M維向量平均值為：

所以，訓練樣本圖的協方差矩陣為：

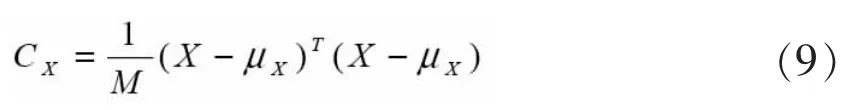
K-L變換后的矩陣為：

式中，P表示訓練集里的總人數，μi是第i個人圖像的平均矢量。從式（9）、式（10）可以看出，通過K-L正交變換后，識別圖像維數降低了，由M-1降到P-1，大大地減少了計算量，但識別率并未下降，下文通過實驗數據驗證。

以N×N的識別圖像為例，其中Cb矩陣的維數是N2×N2，難于通過計算直接得出其特征信息值和正交歸一化矢量。

改進這一不足可用奇異值分解（SVD）算法。用X表示n×r維矩陣，秩為r，這樣就有以下兩個正交矩陣：

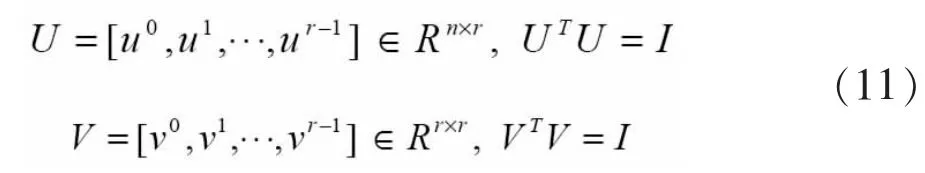
對角矩陣：

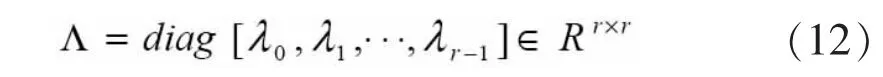
λ0，λ1，…λr-1以降序的方式排列：λ0≥λ1≥…≥λr-1，所以有。

式中，λ1是矩陣XXT和XTX的非零特征值，ui、vi分別是XXT和XTX的特征矢量。這就是矩陣X的奇異值分解算法（SVD），λ1是X的奇異值[1]。

SVD推導過程如下：

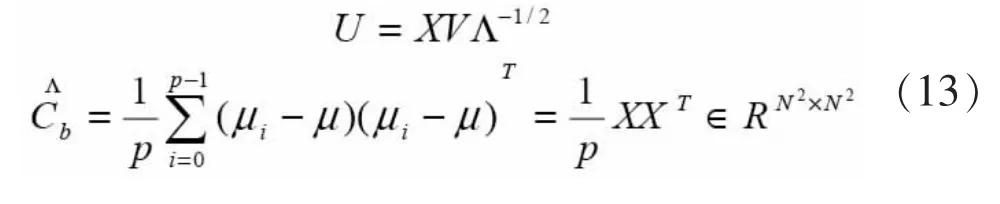
其中：

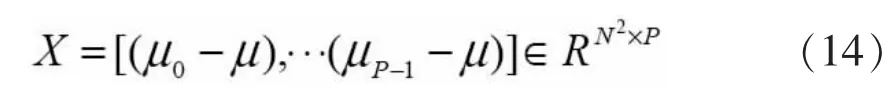
矩陣特征矢量λ1和相對于它的正交歸一化后的特征向量vi很容易求得。

由上面可得，正交歸一化后，Cb的特征矢量如下：

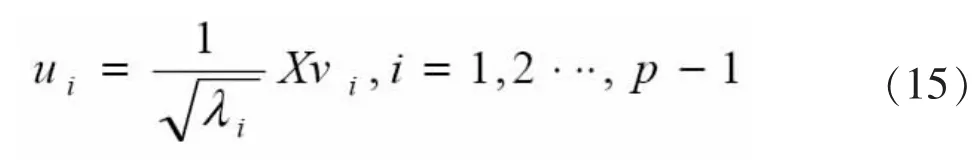
ui就是識別圖像的“特征臉”的矢量，標作：

p（p＜M），人臉識別時P個特征值實際上已經夠用了。所以在計算特征臉時，只需要取M中前面的P個最大特征值所對應的特征向量。對于隨機的一個人臉識別圖X，對特征圖像的子空間進行投影，該投影就是向量X與U的內積：

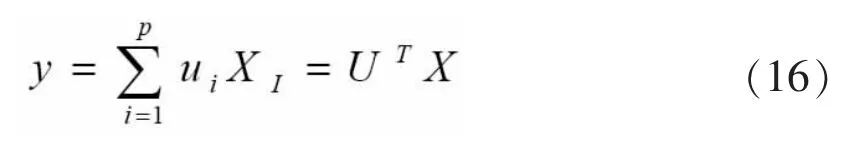
2 實驗流程設計與結果分析

2.1 算法設計和實現

Gabor和PCA融合算法流程圖如圖1所示，具體算法步驟如下：

圖1 Gabor和PCA融合算法流程圖

1）選用并輸入ORL數據庫作為實驗訓練圖。

2）選用光照預處理、標準化處理、圖像增強等預處理算法，選用窗口為5*5的方形中值濾波器。

3）Gabor變換與提取，在范圍[0,π]內采樣，選取8個方向、5個尺度，得到40個分量。

4）PCA降維，用PCA主成分分析法對特征圖像信息進行數據壓縮、降維[12]。根據前面的算法闡述，特征臉圖像的特征維數是M，經過K-L變換后，得到矩

成分分析算法降維。接著采用PCA算法是對特征臉進行降維。根據前文的研究算法，設有特征維數為M的人臉圖像，則：K-L變換后產生矩陣可得到，根據SVD定理，對任意人臉圖像X，將其向特征臉子空間投影，得到列向量。然后使用基于歐氏距離的最近鄰分類器，將特征臉對應的人臉分類出來。

2.2 Gabor與PCA融合算法的人臉識別系統實驗設計

2.2.1 識別系統實驗流程介紹

本實驗流程使用Matlab軟件，以Gabor與PCA融合算法作為核心算法，以此來提取特征的算法，能夠把人臉數據庫中的人臉識別圖像識別出來，且準確率大于95%，實驗系統人為隨機選取數據庫中的圖像。選擇Gabor與PCA融合或是只有PCA這兩種算法，輸出實驗結果。融合算法的系統流程圖如圖2所示。

圖2 融合算法的系統流程圖

2.2.2 Gabor與PCA融合算法識別系統實驗的實現工具

實現工具選用Matlab，這是一款由美國MathWorks公司研發的軟件，在數值分析與數據信號處理、動態建模與系統優化、可視化的人工程序設計方面有廣泛的應用。其編程和計算機速度快、效率高，簡單易學，人機交互強大，在應用程序和圖像處理方面功能強大。

2.2.3 系統軟件主要界面

人臉識別系統軟件主界面如圖3所示，打開圖像界面如圖4所示，識別過程界面如圖5所示。

圖3 人臉識別系統軟件主界面

圖4 打開圖像界面圖

圖5 識別過程界面圖

2.2.4 實驗數據及結果分析

按照論文實驗步驟，本節對Gabor與PCA融合實驗算法的人臉識別系統進行實驗并提取數據進行分析，與單純PCA算法的實驗結果進行比較。

實驗圖像選用ORL人臉數據庫，進行算法驗證。每個人有10幅圖像，選前5幅作為訓練樣本，后5幅作為測試用樣本，分別各有200幅，實驗數據如圖6所示。

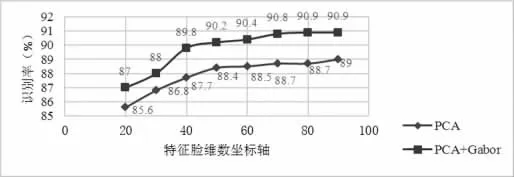
圖6 兩種算法在不同特征臉維數下的識別率對比線

對比圖6中數據可知，把Gabor和PCA融合在一起的算法，其系統識別率大約提高了2%。Gabor算法在繼承和發展傅立葉變換的整體思想上有很大的優勢，能極大地提高識別系統的魯棒性和識別率。而PCA主成分分析法，先統計空間中現有的原始信息，分析數據，篩選出最主要的特征信息，去除其他無用的信息，提高了信息利用率。實驗設計中，先用PCA對數據降維。從圖6中數據可看出，從維數20開始，維數增加，識別率隨之提高，但速度越來越慢；維數繼續增加，系統計算變得更加復雜，識別率提高的速度趨于緩慢，幅度很小。數據分析可以看出，在維數為50左右時，識別率較高，能夠滿足系統要求。

3 小結

本課題具體介紹Gabor與PCA相互融合的人臉識別系統的實驗設計流程，運用Matlab軟件實現了融合算法的實驗仿真，進行了實驗設計并分析了實驗數據。Gabor算法雖然具有較大的識別率和魯棒性，但計算量太大而致使效率降低；PCA是對數據進行降維，再對映射到子空間的信息進行分類再識別，降低數據維數到50，減少了50%的計算量；最后把Gabor與PCA進行融合算法處理，比起傳統的PCA主成分分析法，識別率大約提高了2%。