基于ADMM的間歇采樣轉發式干擾的參數估計
尚東東, 張勁東, 胡婉婉, 王 娜
(南京航空航天大學電子信息工程學院, 江蘇南京 211100)
0 引言
在電子戰領域,假目標干擾是常見的欺騙干擾方式,尤其是基于數字射頻存儲器產生的間歇采樣轉發式干擾,更是得到了廣泛的應用。間歇采樣轉發式干擾與雷達回波信號具有相參性,能夠獲得雷達匹配濾波處理后的脈壓增益,有著較強的干擾能力。因此,針對間歇采樣轉發干擾的參數提取對抑制這種干擾具有重要的理論意義和實用價值。
間歇采樣轉發式干擾是對截獲到的線性調頻信號延時轉發而來的。雖然國內外對線性調頻信號參數估計[1-2]的研究很多。但針對間歇采樣轉發式干擾的參數提取方法研究極少。目前,間歇采樣轉發式干擾的參數估計大都建立在時頻分析的基礎上。文獻[3]對間歇采樣轉發式干擾脈沖壓縮結果進行時頻分析,得到切片的數量,然后通過去卷積處理估計切片的寬度。文獻[4]通過短時分數階傅里葉變換得到干擾時頻分布圖,并通過二值化估計干擾參數。文獻[3]和文獻[4]的方法運算量較大,實現較為復雜,無法滿足雷達實時性的要求;文獻[5]分析干擾匹配濾波后的互模糊函數,然后通過Randon變換和最小二乘估計法對干擾參數進行估計,但是該方法受噪聲影響較大,且Randon變換的復雜度較高;文獻[6]提出一種滑動截斷匹配濾波方法,通過對濾波器長度和濾波器延時進行二維搜索,對干擾參數進行估計,但該方法中搜索的范圍需要先驗信息。因此由于參數提取難度大,目前針對間歇采樣轉發式干擾的參數提取并無有效算法支撐。
ADMM是Gabay提出的一種解決大規模凸優化問題的算法[7]。ADMM相比于其他優化算法有著處理速度快、收斂性能好等特點,在統計學習、圖像處理等領域有著廣泛的運用。
綜上,本文提出一種基于ADMM的間歇采樣轉發式干擾的參數估計方法。該方法根據間歇采樣轉發干擾脈沖壓縮結果,構造出含有加窗向量的非線性整數優化模型,將參數估計問題轉化為加窗向量估計問題,然后利用ADMM將非線性整數優化模型分解為整數歸整模型與連續模型,實現切片寬度和數量的估計。
1 間歇采樣轉發式干擾的參數估計模型
間歇采樣轉發式干擾是在干擾機截獲到雷達發射信號后,對發射信號進行采樣,將采樣的信號按照一定的規律轉發出去,直至雷達發射信號結束。其工作原理如圖1所示。
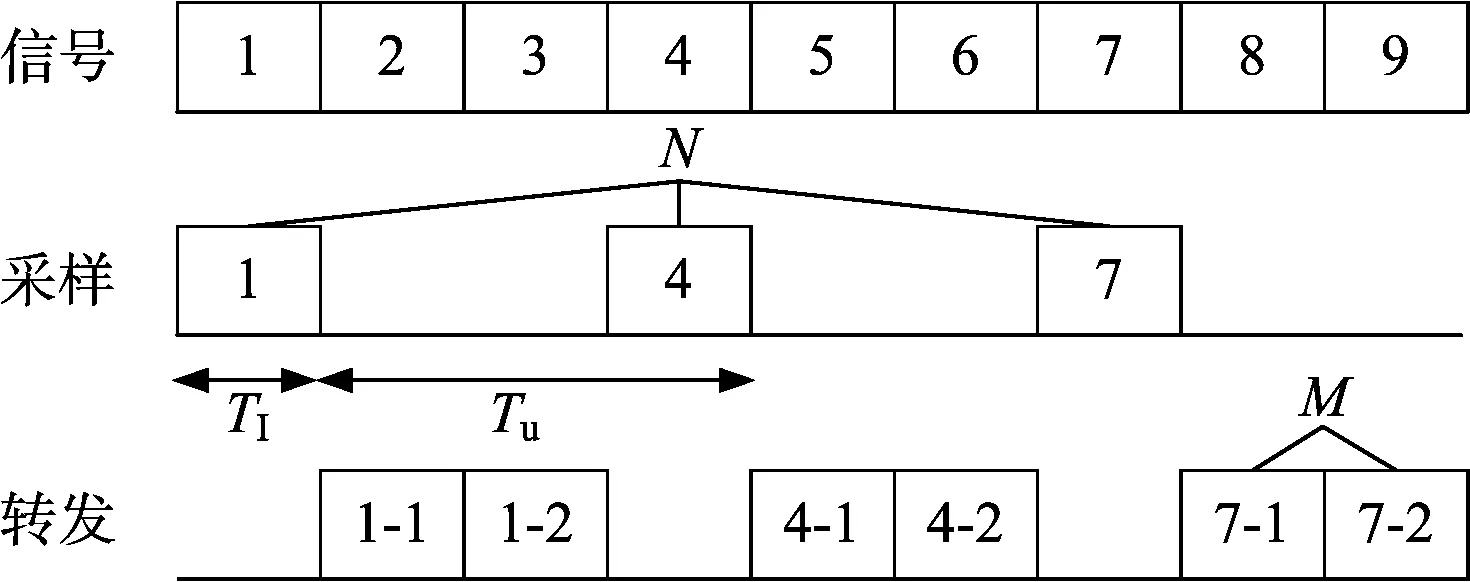
圖1 間歇采樣轉發式干擾(K=3,M=2)
雷達發射的線性調頻信號可表示為
(1)
式中,Tp為脈寬,Kr=B/Tp為調頻斜率,B為信號帶寬,f0為載頻。
則干擾機截獲到雷達信號后,對其進行間歇采樣處理,采樣后的切片信號可表示為
(2)
式中,TI為切片的寬度,K為切片的數量,Tu=(M+1)TI為間歇采樣的周期,M為切片的轉發次數,τ為轉發延遲和傳播延遲。
采樣的切片轉發M次之后,間歇采樣轉發式干擾信號表示為
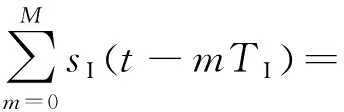
ejπKr(t-τ-mTI)2
(3)
間歇采樣轉發式干擾形式主要有直接轉發干擾、重復轉發干擾和循環轉發干擾,本文只針對直接轉發干擾進行研究,即M=1。直接轉發干擾是在干擾機截獲到雷達發射信號后,對發射信號進行采樣,直接將采樣的信號轉發出去,然后重復此過程直至雷達發射信號結束。為方便分析,這里設傳播延遲為0,直接轉發干擾信號可表示為
sJ1(t)=sI(t-TI)=
(4)
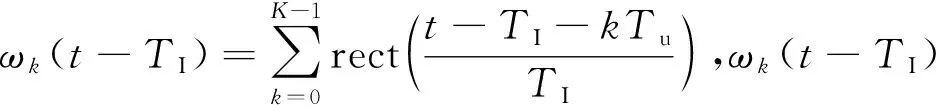
sJ2(t)=ωk(t-TI)ejπk(t-TI)2=
ωk(t-TI)x(t-TI)
(5)
令t=nTs,TI=NITs,Tu=NuTs(Ts為采樣周期),則式(5)可變為
sJ2(n)=ωk(n-NI)x(n-NI)=
(6)
式中,N為一個周期的采樣點數。
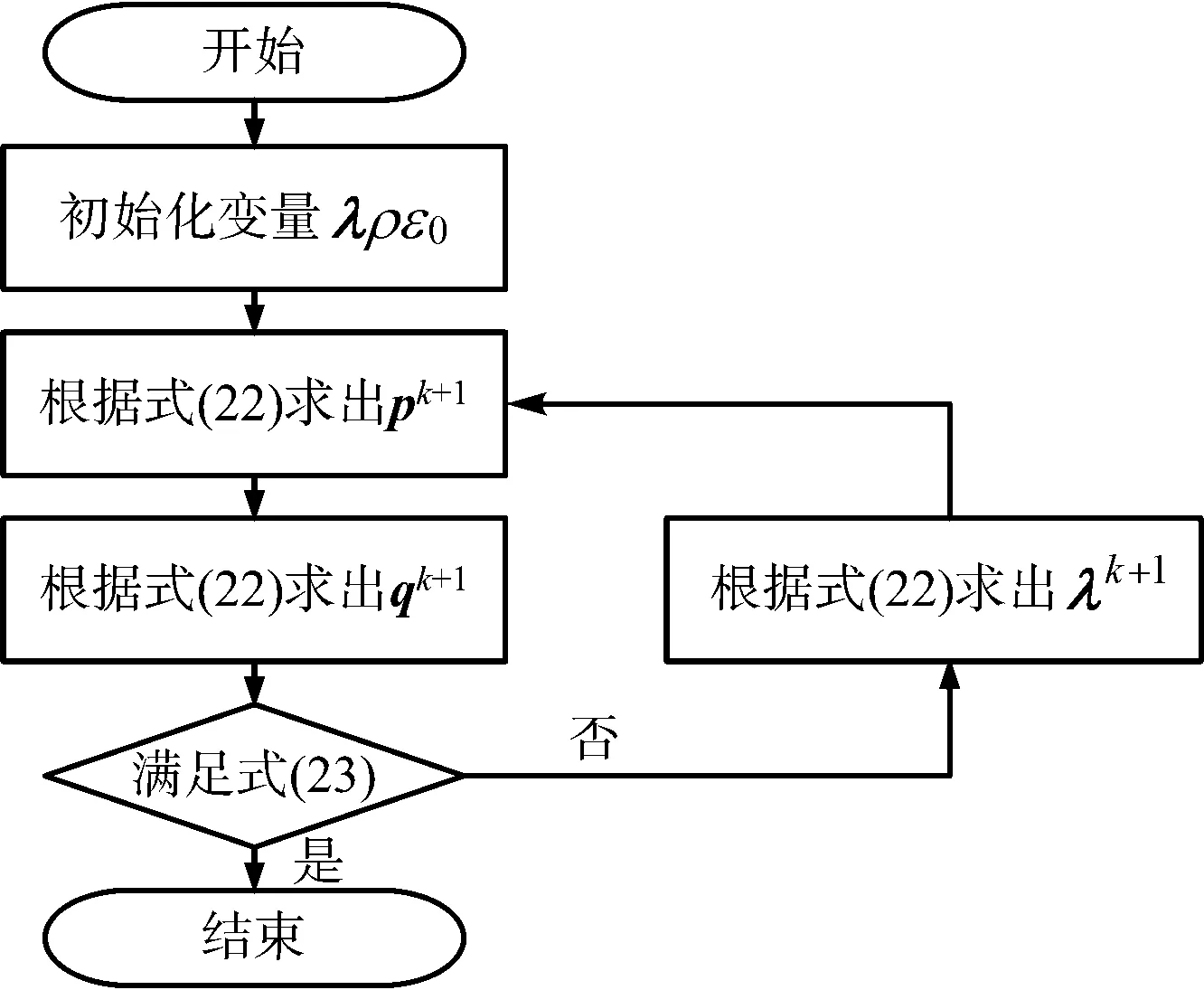
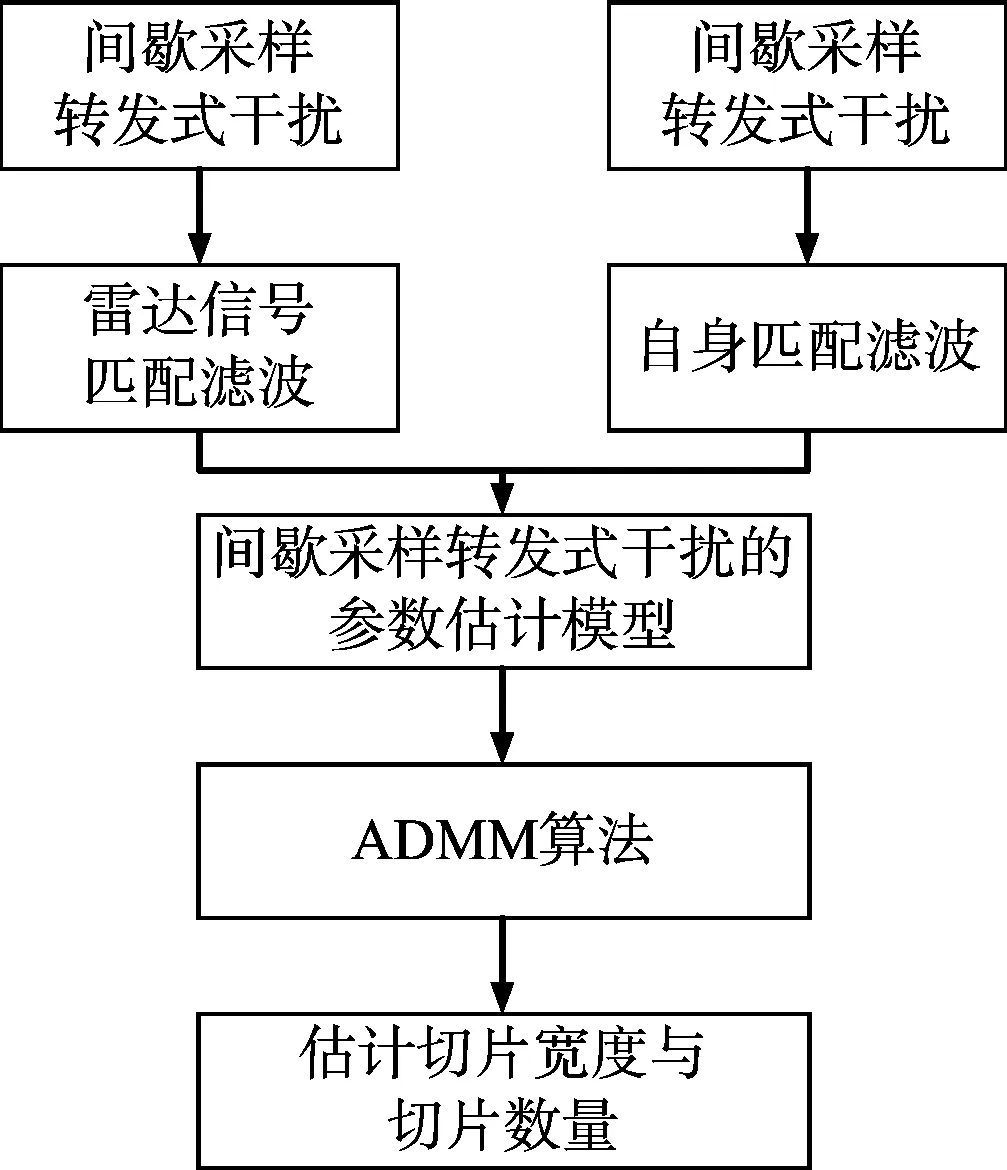
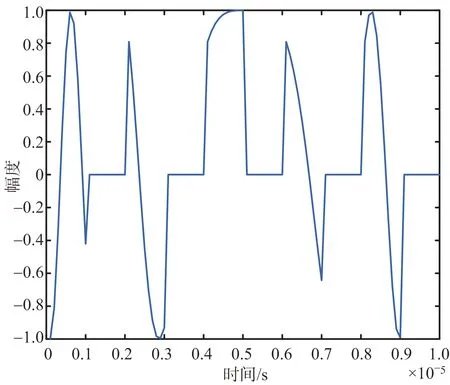
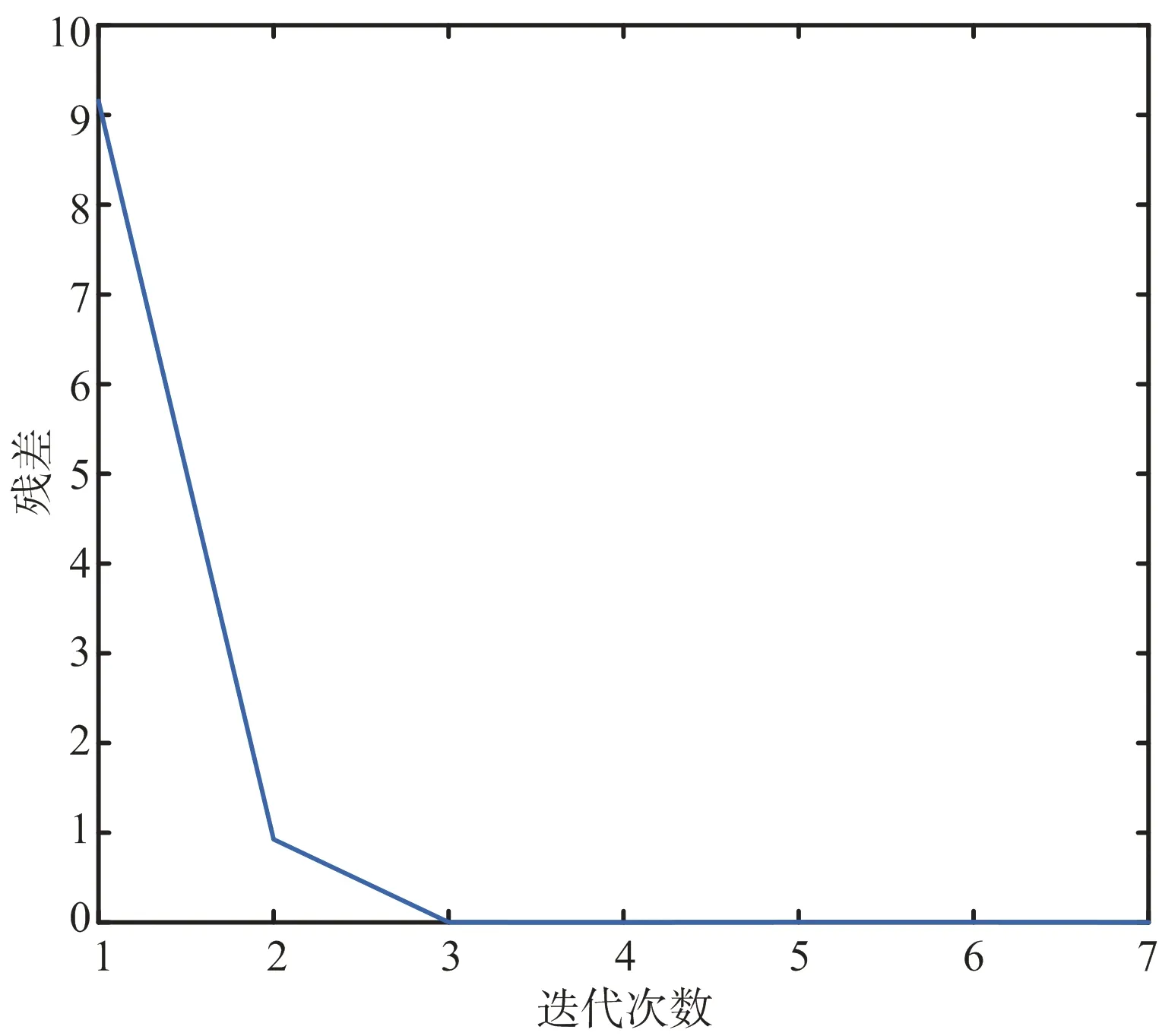
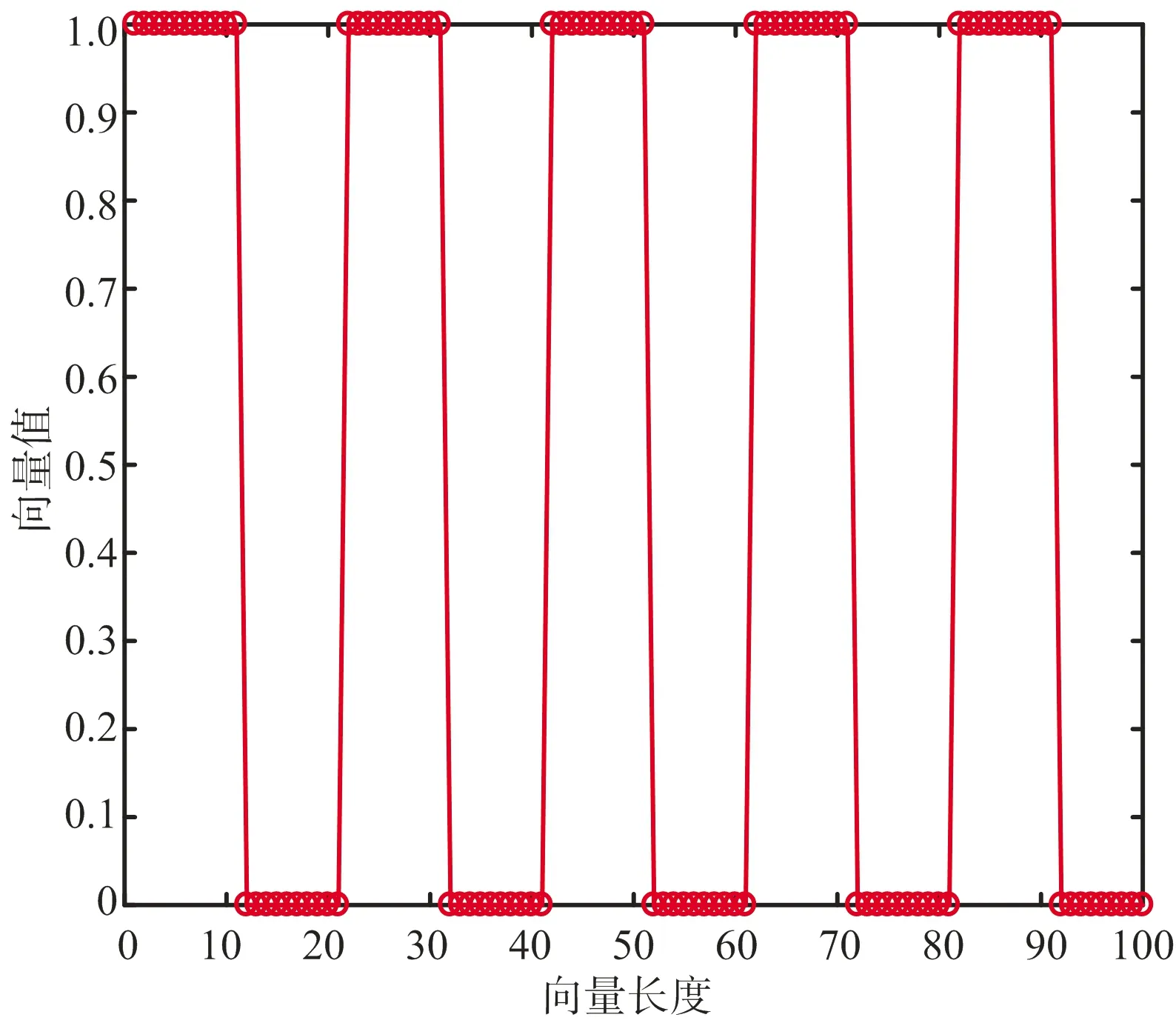
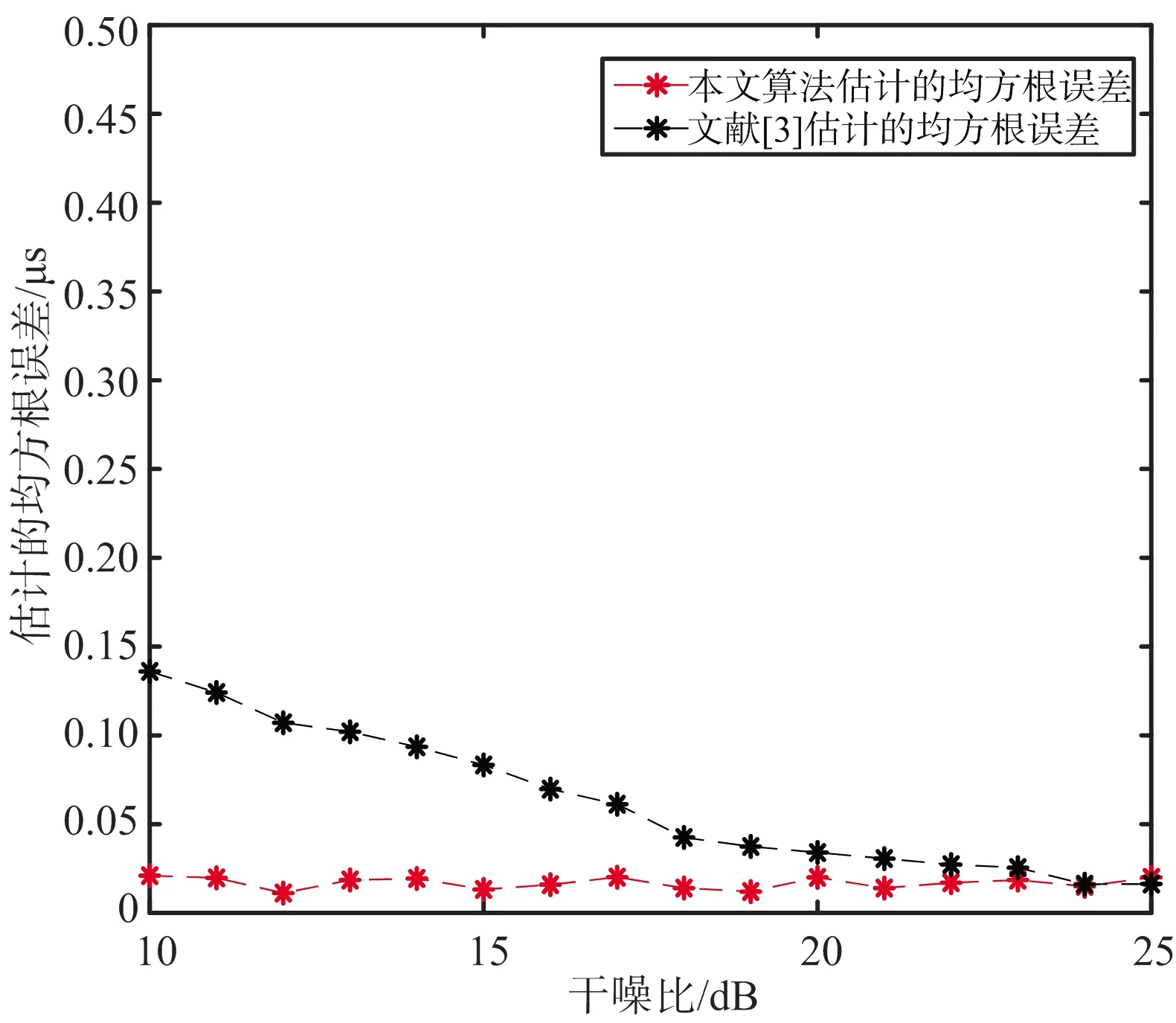
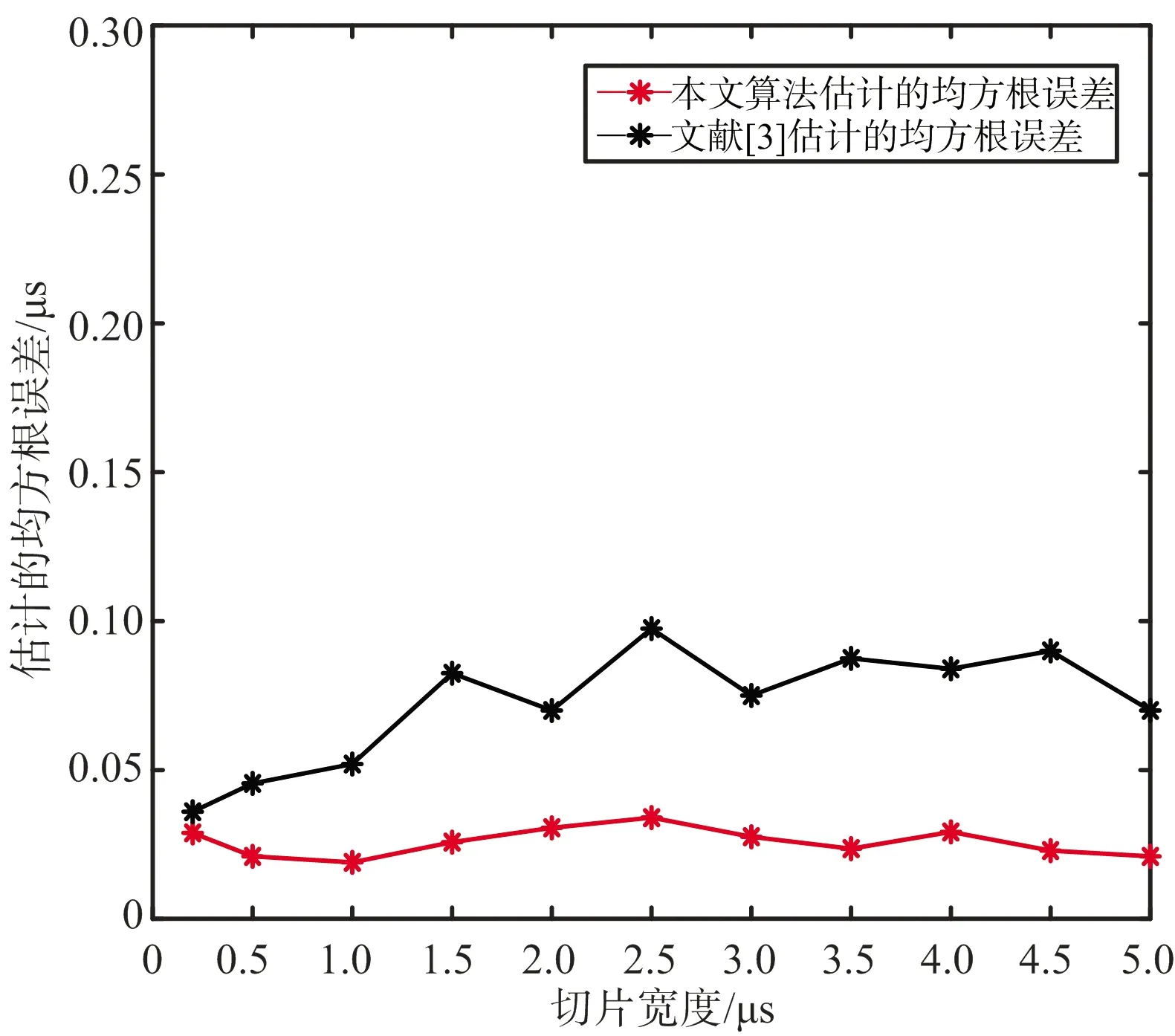
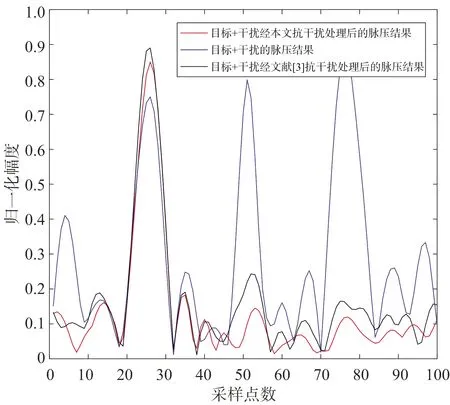
設匹配濾波器的響應為h(n),NI (7) 相應的振幅響應為 (8) 從上面可以看出,間歇采樣轉發式干擾信號實質上是將截獲的雷達信號頻譜搬移到辛格函數每條離散譜線處,多個干擾切片疊加后相當于對辛格主瓣進行了采樣。間歇采樣轉發式干擾經匹配濾波之后的振幅響應取決于切片的數量K與切片的寬度TI。因此,切片數量K與切片寬度TI的估計可以通過匹配濾波器實現。而這兩個關鍵參數與窗函數ω(t-TI)形式有關,則對干擾信號切片寬度與切片數量的估計問題可轉化為窗函數的估計問題。 設未知窗函數為q(n),則間歇采樣轉發式干擾用窗函數可以表示為 sJ(n)=q(n)⊙s(n) (9) 式中,⊙表示點乘,s(n)為雷達信號。 雷達接收到信號(包含目標、切片干擾和噪聲)為 (10) 式中,w(n)為高斯白噪聲,s(n)為雷達信號,sJ(n)為干擾信號,αt為雷達信號的系數,αs為干擾信號的系數。 間歇采樣轉發式干擾分別經雷達信號匹配濾波和自身匹配濾波后之差可表示為 r0(n) (11) 在已知間歇采樣轉發式干擾的窗函數,則式(11)兩種匹配處理之差應非常小,在理想情況下為0。為了衡量上式兩種處理方法之差,這里取無窮范數,可得 ||f[q(n)]||∞=||Hq||∞ (12) 式中,矩陣H為系數矩陣,q為加窗向量,待估計值。 當||f[q(n)]||∞取最小值時,雷達信號加窗之后的結果最接近于間歇采樣轉發干擾信號。據此,本文可將參數估計問題轉化為目標函數優化問題,從而實現干擾信號切片寬度與切片數量的估計。為了使參數估計模型求解時獲得稀疏解,并且防止過擬合,在式(12)中加入正則化項,本文間歇采樣轉發式干擾參數估計模型為 (13) 式中,||q||1為正則項。 分析式(13)可以發現其屬于非線性整數規劃問題。目前,解決非線性整數規劃問題的傳統方法主要有分支定界法[8-9](Branch-and-Bound,BB)、廣義Benders分解法[10](Generalized Benders Decomposition,GBD)等。但BB在處理大規模優化問題中速度較慢,GBD在針對非凸問題時,子問題的最優解不能準確地傳遞給主問題。因此,這些算法在求解非線性整數優化問題時時間復雜度都較高。 ADMM算法融合了對偶上升法的可分離性以及乘子法的收斂性,核心思想是將一個大的問題分解成若干個小問題,交替迭代進行求解,使原目標與對偶變量共同收斂[11],其標準形式如下[12]: (14) 式中,f(x),g(z)為2個凸函數。 構造拉格朗日函數: Lp(x,z,λ)=f(x)+g(z)+λT(Ax+Bz-c)+ (15) 式中,Lp(x,z,λ)為增廣拉格朗日函數,λ為對偶變量,ρ>0為懲罰系數。則k+1次更新迭代形式為 (16) 根據式(16)可知,ADMM算法首先分別求解x和z兩個變量,然后根據x和z再對λ求解。算法迭代時,x和z是交替更新的,這個過程稱為交替方向過程[13-14]。 對于非線性整數優化問題,ADMM算法可將其分解后形成兩個小的子問題:整數歸整問題、連續問題,通過縮小問題的規模來增加求解的彈性。具體做法是復制一個和整數變量有相同邊界的連續變量,代替整數變量參與連續問題的優化。根據ADMM算法原理,將式(13)寫成如下緊湊形式: (17) p-q=0 (18) 當對式(13)中的整數變量q進行復制,使其連續變化,就得到了式(17)中的變量p,變量p與變量q有相同的邊界條件。式(18)為它們之間的耦合關系,目的就是為了保證p代替q參與連續問題優化后,得到的最優解能一致收斂到q。將式(17)和式(18)寫成增廣拉格朗日罰函數的形式,則目標函數為 L(p,q,λ)=F(p)+λT(p-q)+ (19) 根據ADMM的更新迭代形式,將待優化模型分解得到兩個規模較小的子模型,如式(20)所示是只包含變量p的非線性規劃模型,如式(21)所示為只包含變量q的混合整數二次規劃模型。 (20) (21) 式中,k為更新迭代次數。 根據式(20)和式(21)可知,非線性規劃模型對應式(13)的松弛模型,混合整數二次規劃模型對應式(13)的整數歸整模型。 則k+1次更新迭代形式為 (22) 根據ADMM的收斂條件,當第k+1次迭代完成后,qk+1與pk+1之間的殘差達到收斂精度時,迭代停止,得到最優解qk+1,收斂判定條件如式(23)所示。圖2為ADMM算法的流程圖,圖3為間歇采樣轉發式干擾的參數估計流程圖。 ε=||pk+1-qk+1||2<ε0 (23) 式中,ε0為迭代停止基準,本文取0.001。 圖2 ADMM算法流程 圖3 間歇采樣轉發式干擾參數估計流程 仿真參數設置如下:線性調頻信號B=2 MHz,時寬T=10 μs,采樣頻率fs=5B,干擾采樣周期Tu=0.2T,占空比r=0.5,殘差迭代停止基準ε0=0.001,背景為高斯白噪聲。圖4為間歇采樣轉發式干擾信號的時域波形。 圖4 間歇采樣轉發式干擾信號的時域波形 圖5是在干噪比JNR=14 dB,ρ=0.9下的殘差收斂曲線圖。殘差是判斷ADMM算法是否達到最優的一個重要標準。由圖5分析可知:殘差隨著迭代次數的增加而減小,在迭代相應的次數后,其值趨近于零,說明該算法良好的收斂性。圖6為上述條件下估計的加窗向量,從圖中可以精確地得到切片數量,而切片寬度存在一定的誤差。 圖5 殘差收斂曲線 圖6 估計得到的加窗向量 為了驗證本文算法的有效性,在JNR=10~25 dB,ρ=0.9時分別進行100次蒙特卡洛仿真,計算每個JNR下估計切片寬度的均方根誤差,將本文結果與文獻[3]比較,圖7為2種算法估計切片寬度均方根誤差圖,從圖中可以發現本文算法隨著JNR增大,估計均方根誤差在減小,JNR≥10 dB時估計的均方根誤差在0.02 μs左右,估計的精度較文獻[3]有較大提高,且受噪聲的影響更小。實驗證明了該方法的優越性。 圖7 2種算法估計切片寬度的均方根誤差 為了研究切片寬度對本文算法的影響,在JNR=14 dB,ρ=0.9時分別進行100次蒙特卡洛仿真估計,計算不同切片寬度下估計切片寬度的均方根誤差,圖8為估計的均方根誤差隨切片寬度變化曲線圖。從圖中可以看出本文算法受切片寬度的影響較小,估計均方根誤差更小。 圖8 估計的均方根誤差隨切片寬度變化曲線 為了測試使用本文算法抗干擾的效果,將雷達接收信號的干擾區間置零,即 s(t)+sJ(t)=0 (24) 式中,s(t)為目標信號,sJ(t)為間歇采樣轉發式干擾信號,t∈[nTu+TI,(n+1)Tu],將雷達接收信號的非零部分作拼接處理,然后將拼接處理后的信號進行匹配濾波處理。圖9為利用本文算法提取的參數抑制干擾的效果圖。從圖中可以看出目標回波疊加間歇采樣轉發式干擾信號經過抗干擾處理后,假目標被成功抑制掉,且比文獻[3]的抗干擾效果好。 圖9 抗干擾處理前后的對比圖 間歇采樣轉發式干擾與雷達信號具有相參性,在時域上能夠形成大量且逼真的假目標。針對間歇采樣轉發的問題,本文以間歇采樣轉發干擾的模型為基礎,推導出干擾經過脈沖壓縮后的結果,構造含有加窗向量的非線性整數優化模型,最后巧妙利用ADMM算法求解加窗向量,實現切片寬度和數量的估計。仿真結果表明在干噪比10 dB以上時,該方法估計參數的精度較其他方法有明顯提高且更加穩定。由于間歇采樣轉發式干擾能夠通過調整參數形成不同的干擾樣式,針對其他干擾樣式的參數估計是下一步的研究方向。
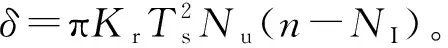
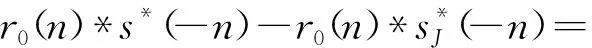
2 基于ADMM的間歇采樣轉發式干擾的參數估計算法
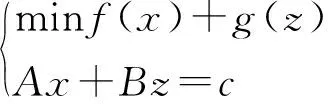
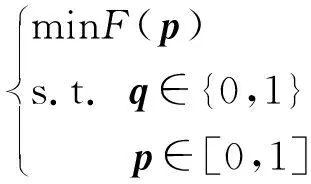
3 仿真分析
4 結束語

