波導阻抗帶寬與縫隙導納關系研究

李 雁, 盧曉鵬, 盛 磊

(中國電子科技集團公司第三十八研究所， 安徽合肥 230088)

0 引言

縫隙波導諧振天線具有效率高、交叉極化低、帶內波束指向色散小、功率容量大、機械強度高、環境適應性好等諸多優點，在星載相控陣雷達和通信系統中得到了廣泛應用，如國外的TerraSAR-X、Sentinel-1、Almaz-1和國內的海絲1號等SAR系統輻射陣面皆采用了縫隙波導諧振陣。但縫隙波導諧振天線的突出缺點是帶寬窄，這限制了它在寬帶高分辨軍用和民用SAR領域的應用。

為實現縫隙波導諧振陣的寬帶設計，很多文獻對此進行了研究和討論。理論上，文獻[1]給出了諧振陣的輸入駐波比與縫隙數目N及帶寬B之間的近似關系。但此關系未計入縫隙間距對工作帶寬的影響，同時其計算獲得的最大帶寬相比工程實踐明顯偏小。文獻[2]從諧振陣等效電路出發，建立了諧振陣實現口徑等幅同相激勵的理想電納條件，給出了諧振陣實現方向圖最大帶寬的導納設計方向。工程上，公開文獻主要從改變縫隙形狀[3-4]、子陣化[5-6]和差分饋電[7]等方面探索了展寬縫隙波導陣阻抗帶寬的實現方法。其中改變縫隙形狀的技術措施會帶來交叉極化的惡化以及加工難度的增加。而子陣與差分饋電技術則會帶來天線復雜度與厚度的增加。為此希望能從理論上探索出一種實現單層波導諧振陣帶寬最大化的分析方法，為阻抗帶寬的優化設計提供依據。

本文首先從諧振陣等效網絡出發，研究了縫隙諧振陣實現理想阻抗匹配時所需的導納特性，并建立并聯縫隙等效電路，實現縫隙導納特性的單參數表征，據此提出了一種諧振陣實現最大帶寬的導納特性分析方法，建立了諧振陣不采用過載技術時實現最大帶寬的通用公式。同時研究了縫隙寬度對導納特性與阻抗帶寬的影響情況，最后進行了全波仿真設計驗證。

1 寬帶設計對縫隙導納需求分析

1.1 理論依據

縫隙波導諧振陣通常采用并聯縫隙形式進行設計，以矩形波導寬邊開偏置縱向縫為例，其天線模型與等效電路如圖1所示。

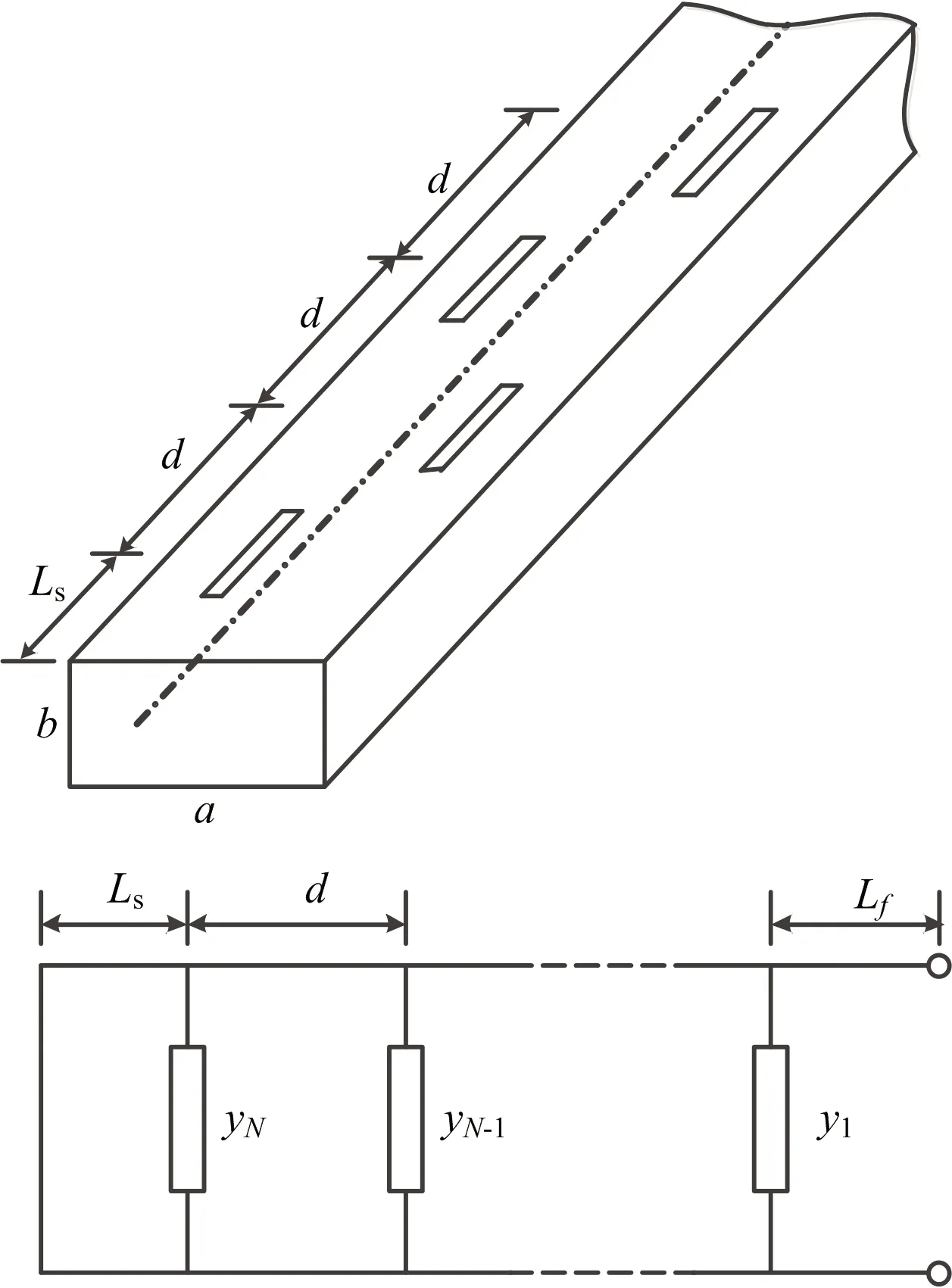
圖1 縫隙波導諧振陣等效電路

對均勻加權縫隙陣，為了簡化分析過程，可設yn=y(n=1,2,…,N)，根據微波網絡理論，并聯電導、短路波導段、并聯電導之間波導段以及饋電波導段的T矩陣為

(1)

(2)

(3)

(4)

式中，B為波導的傳播常數。由此得到整個網絡的T矩陣為

(5)

在縫隙波導諧振陣末端短路的情況下，可推導出端口反射系數為

(6)

(7)

若已知縫隙導納y，則由式(7)計算端口匹配特性；反之若需要縫隙波導端口匹配，則可取S11=0。通過求解下式方程，得到實現縫隙波導諧振陣寬帶理想匹配下各頻率點的所需的導納值。

(8)

1.2 縫隙數對縫隙導納的影響

工程上縫隙波導諧振陣的最大特點是單根波導上饋電縫隙數越多帶寬越窄，首先分析理想匹配情況下縫隙數對縫隙導納的需求情況。不失一般性，這里以中頻5.4 GHz的縫隙波導諧振陣開展實例分析。取d=40 mm=0.72λ0，LS=20 mm，Lf=20 mm，對應矩形波導寬邊尺寸a=38.55 mm。由式(8)所列方程求解出不同縫隙數對應的理想歸一化導納曲線，如圖2所示。這里的導納曲線按諧振電導最大值進行歸一化處理(以下將此電導、電納稱為歸一化電導與歸一化電納)，這是基于Stegen從標準波導孤立單元縱向偏置縫隙大量的測試數據中發現，同一波導口徑下，以歸一化導納為縱坐標，以縫隙長度與諧振長度之比為橫坐標，不同偏置縫隙的歸一化導納特性基本一致。

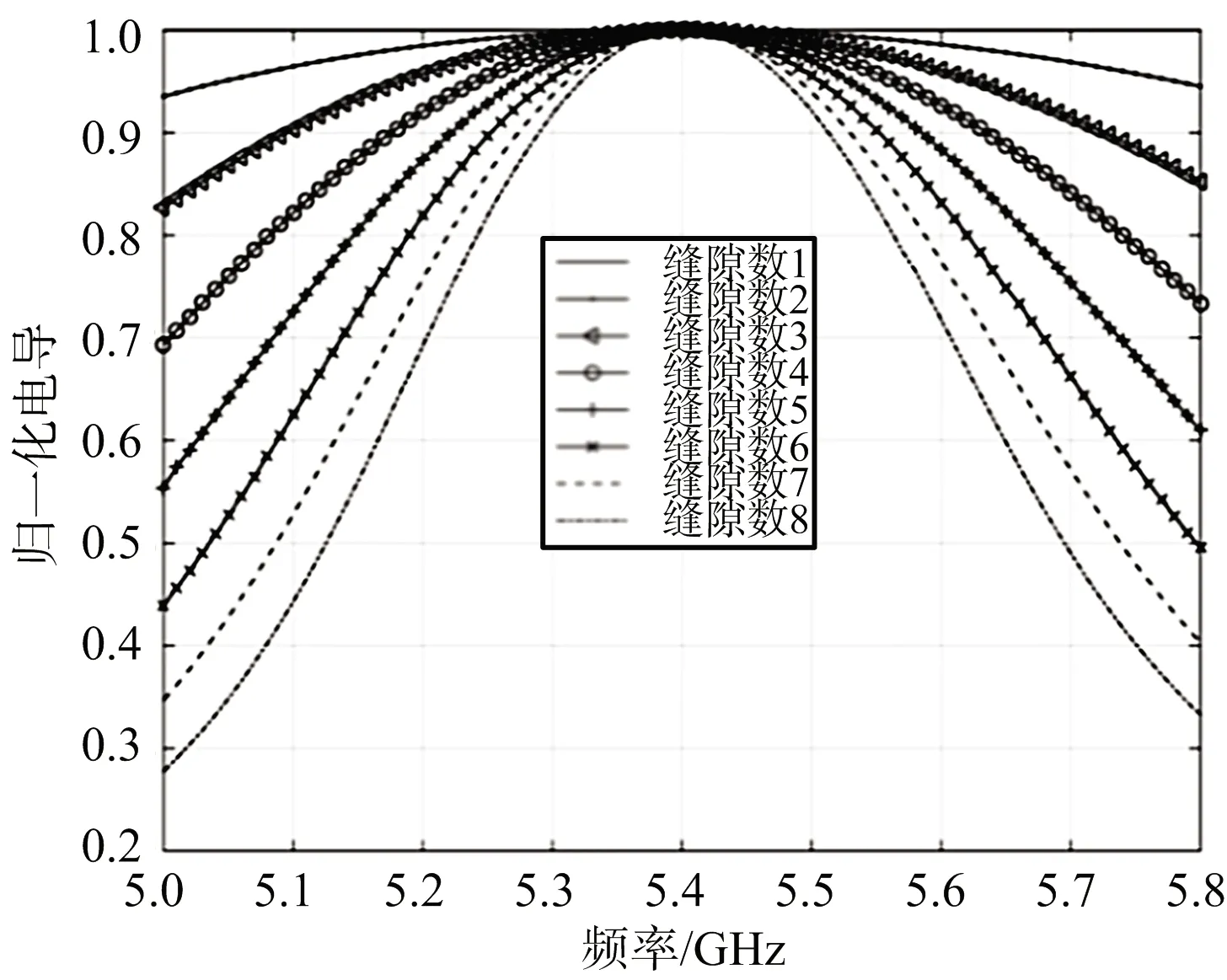
(a) 電導特性

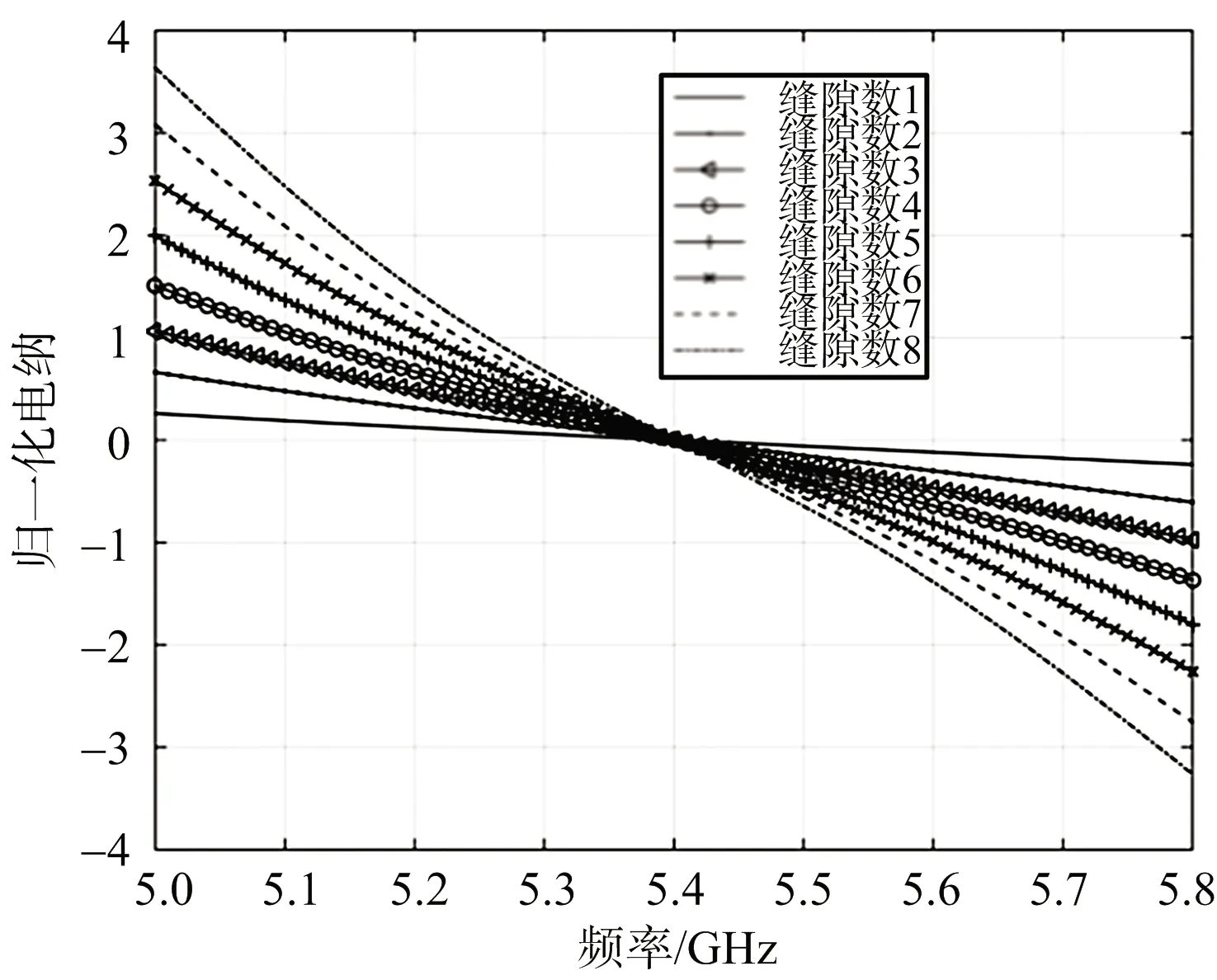
(b) 電納特性圖2 理想匹配時不同縫隙數的歸一化導納曲線

由分析結果可見，對于不同的縫隙數，理論上存在對應的導納特性，可實現裂縫波導諧振天線的理想匹配。縫隙數越少理想匹配時要求歸一化導納變化越平緩，且電納需求隨頻率變化具有單調下降趨勢。即縫隙數越少，要求縫隙導納的變化越平緩，諧振性越弱。很容易理解當縫隙數為1時，要求其電導值為1，而電納值只需要補償1/4波長短路段引入的電納。

1.3 縫隙間距對縫隙導納的影響

工程設計時縫隙單元間距也是需要考慮的設計參數，為此對縫隙數固定且單元間距變化情況下，理想匹配對縫隙導納的需求情況進行研究。這里以5單元縫隙波導諧振陣開展實例分析，單元間距分別取d=35,40,46 mm，結果如圖3所示。可見縫隙間距越大，縫隙的諧振性需求也越強。

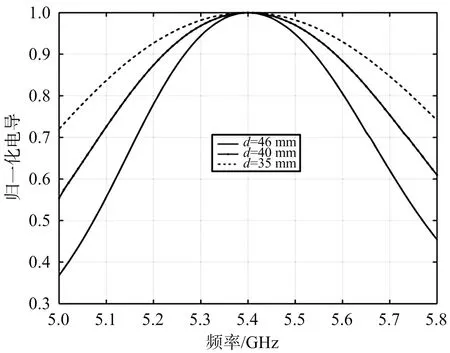
(a) 電導特性

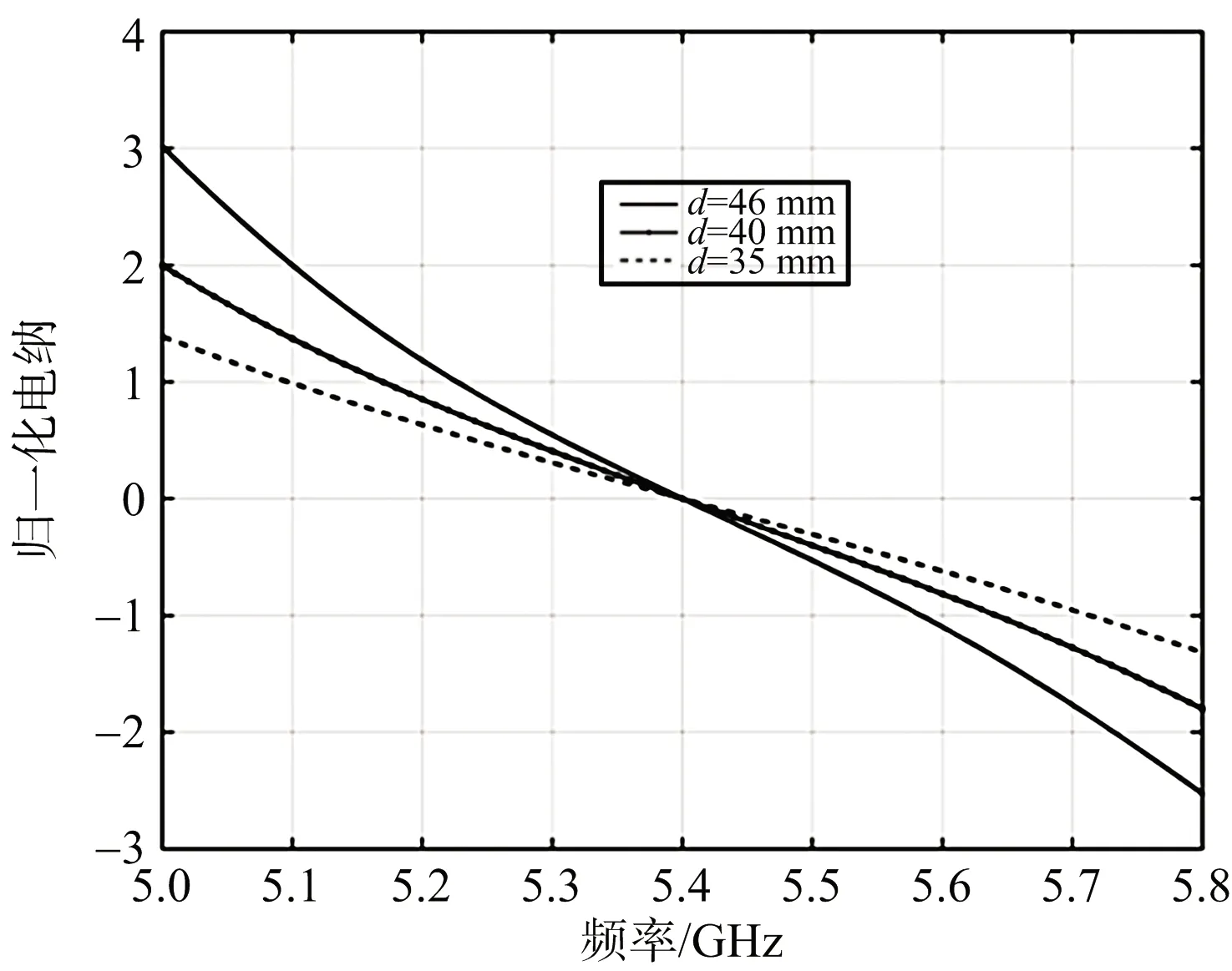
(b) 電納特性圖3 理想匹配5單元線陣不同縫隙間距的導納曲線

綜上，對于特定縫隙數和縫隙間距的波導諧振陣，理論上存在適當的縫隙導納特性可實現天線端口全帶寬的理想阻抗匹配。

2 縫隙等效電路與諧振陣最大帶寬

2.1 并聯諧振縫隙的等效電路

從物理概念上看，縫隙導納的頻率特性主要由縫隙自身決定，導納的絕對值由饋電波導的形狀及在波導上的偏置決定，這一特性可由Stegen的研究結果所證實。因此，對于特定波導結構的同樣縫隙可用一個等效電路進行表征。

根據文獻[8]的波導并聯縫隙等效電路模型，并參考與縫隙互補的偶極子等效電路[9]，將波導并聯縫隙等效為一個RLC串聯電路，建立了波導并聯縫隙天線單元等效電路，如圖4所示。據此可計算出在諧振頻率不變的情況下，串聯電容變化所引起的天線歸一化導納特性的變化曲線，如圖5所示。可見，電容變化將改變天線的頻帶諧振特性，且電容越大導納的諧振性越弱。即縫隙導納的頻率特性可用電容C進行計算。

當然，通過職業院校技能大賽，也反映出了我們在教學中的一些薄弱環節。如教學投入不足，教學實習和實訓設備不夠完善，選手不能適應競賽中采用的現代企業新設備、新技術、新流程，或在規定時間內完成不了比賽任務；基礎理論課教學與專業技能訓練沒有有機結合。應大力推行教學做一體化模式，使車間與教室合二為一，理論與實踐有機融合，努力培養更多高素質、技能型專業人才和實踐應用型能工巧匠。

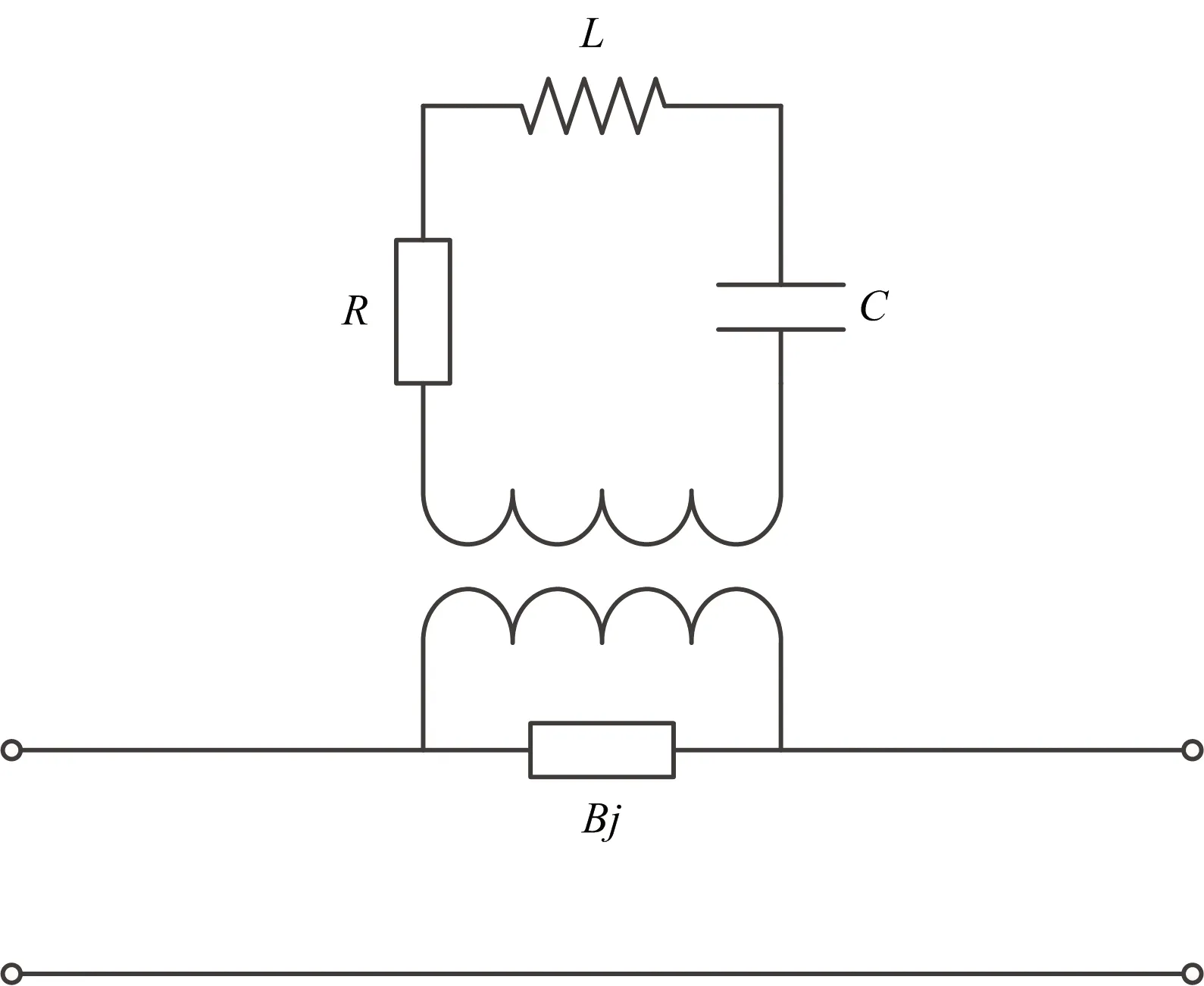
圖4 波導并聯縫隙天線單元的等效電路

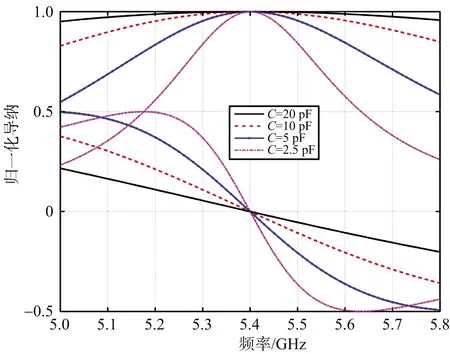
圖5 縫隙歸一化導納受串聯電容影響的分析曲線

2.2 諧振陣帶寬分析方法與可實現的最大帶寬

基于圖4給出的縫隙等效電路，可建立不同縫隙數、不同單元間距諧振陣獲得的最大阻抗帶寬的分析方法。具體過程是，針對特定縫隙數的波導諧振陣，通過調整串聯電容值，使得導納特性逼近理想匹配時導納曲線。然后將此導納曲線帶入公式(7)，分析出此導納特性下的帶內駐波。最后再進一步微調串聯電容值，在不采用過載技術的情況下(即中頻理想匹配)，優化得到此縫隙數下的最大駐波帶寬和對應串聯RLC等效電路表征的最優導納特性曲線。

不失一般性，仍以中頻f0=5.4 GHz、dx=40 mm=0.72λ0的縫隙波導諧振陣為例開展分析。采用此方法在最大駐波比分別限定在1.5和2的情況下，得到不采用過載技術時不同縫隙數的諧振陣最大可實現帶寬,如表1所示。圖6給出最大駐波比為1.5時，不同單元的諧振陣的最優RLC電路導納特性曲線。可見該曲線與理想匹配情況類似，單元數越少導納的諧振特性需求也越弱。

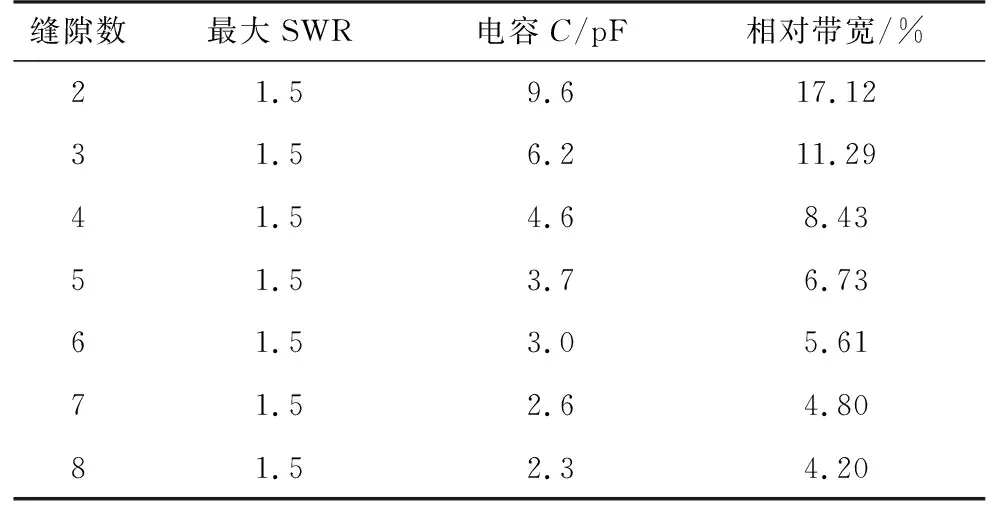
表1 串聯RLC電路dx=0.72λ0端饋諧振陣最大帶寬

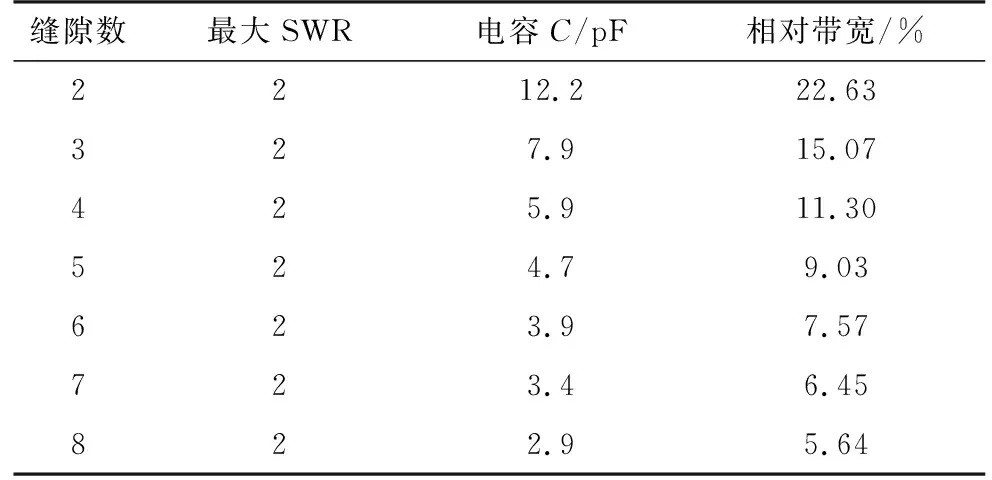
續表

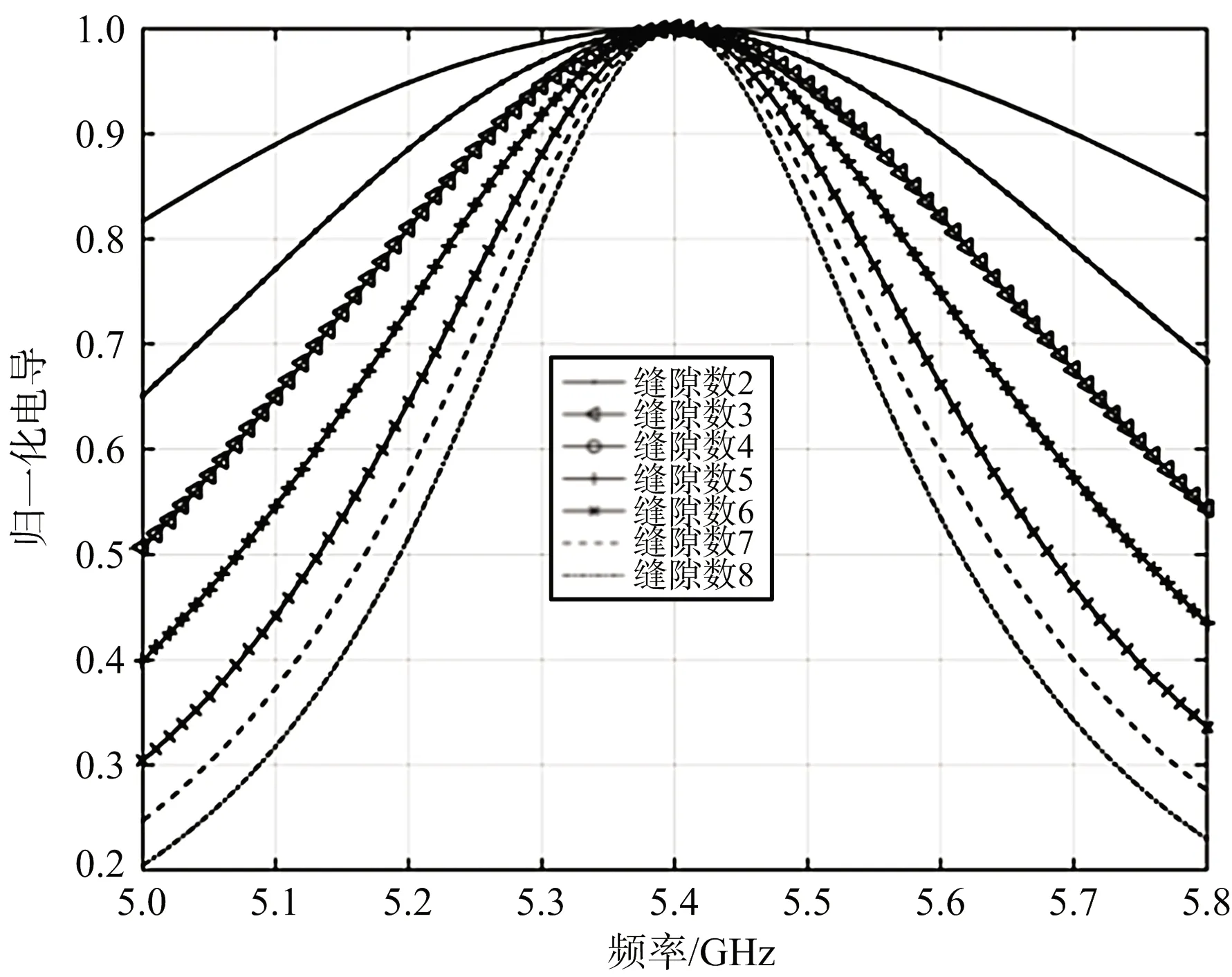
(a) 電導特性

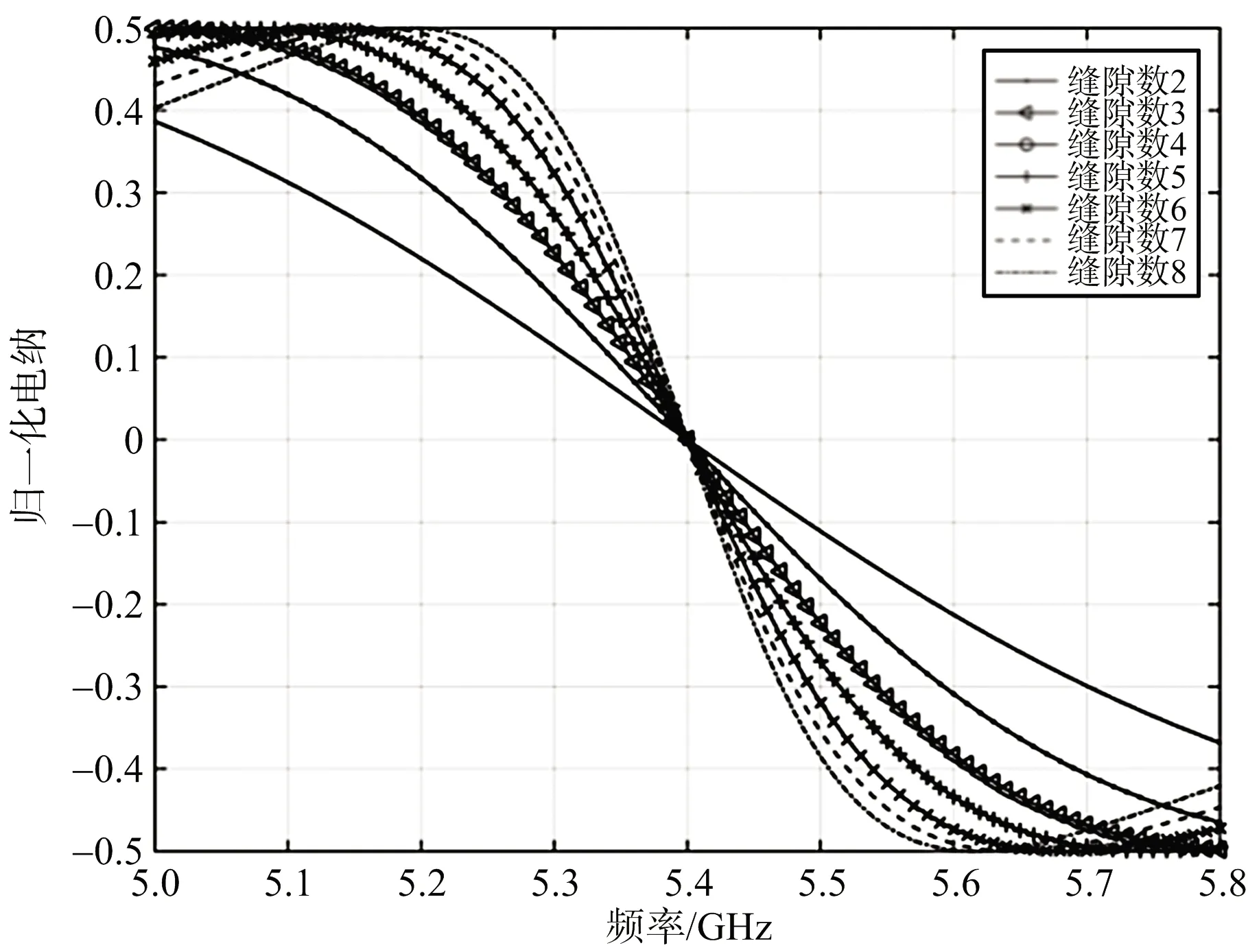
(b) 電納特性圖6 不同縫隙數RLC電路最優導納曲線

將RLC電路分析出的最大帶寬與文獻[1]擬合公式的結果進行對比，如圖7所示。可見，帶寬隨單元數的變化趨勢兩者相同，但同樣單元數目的情況下，基于RLC電路得出的天線最大帶寬明顯優于文獻[1]結果。

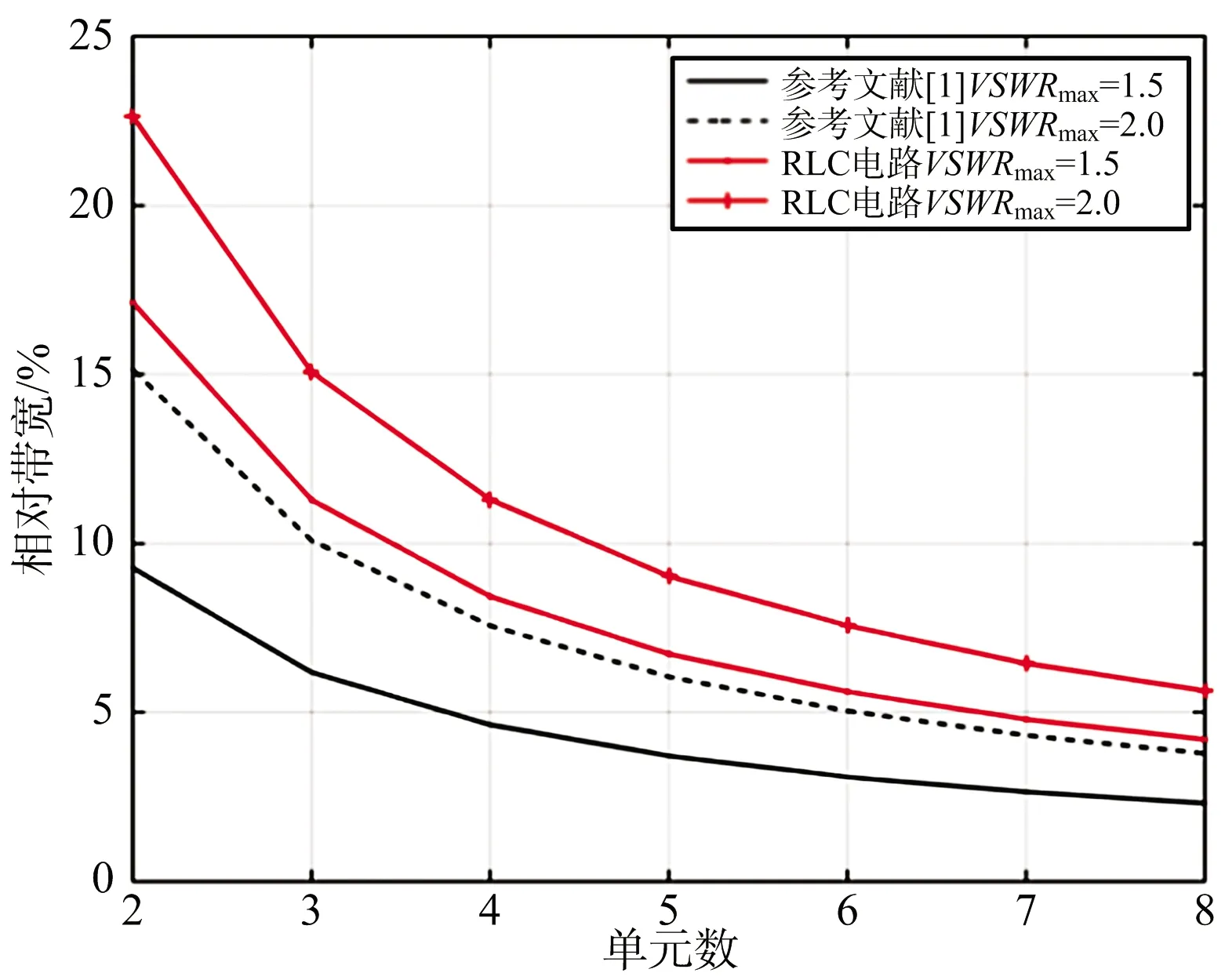
圖7 縫隙數與帶寬之間的關系曲線(dx=0.72λ)

由表1還可以看出，不同的最大駐波條件，RLC電路對應的電容不同，為比較這種導納特性需求差異，以縫隙單元數6為例，圖8分別給出了最大駐波比為1.5和2時，帶寬最優串聯RLC電路的導納特性與理想匹配時的比較。可見，單純RLC串聯電路無法實現諧振陣全頻帶的理想匹配，因為RLC串聯電路的電導與電納特性難以同時逼近理想匹配條件，特別是電納特性在邊頻遠離理想匹配條件。因此串聯RLC電路的最優匹配結果是電導、電納相對于理想匹配條件的折中。此外，允許的最大駐波越大，RLC電路的最優電導曲線越接近理想匹配時的電導曲線。

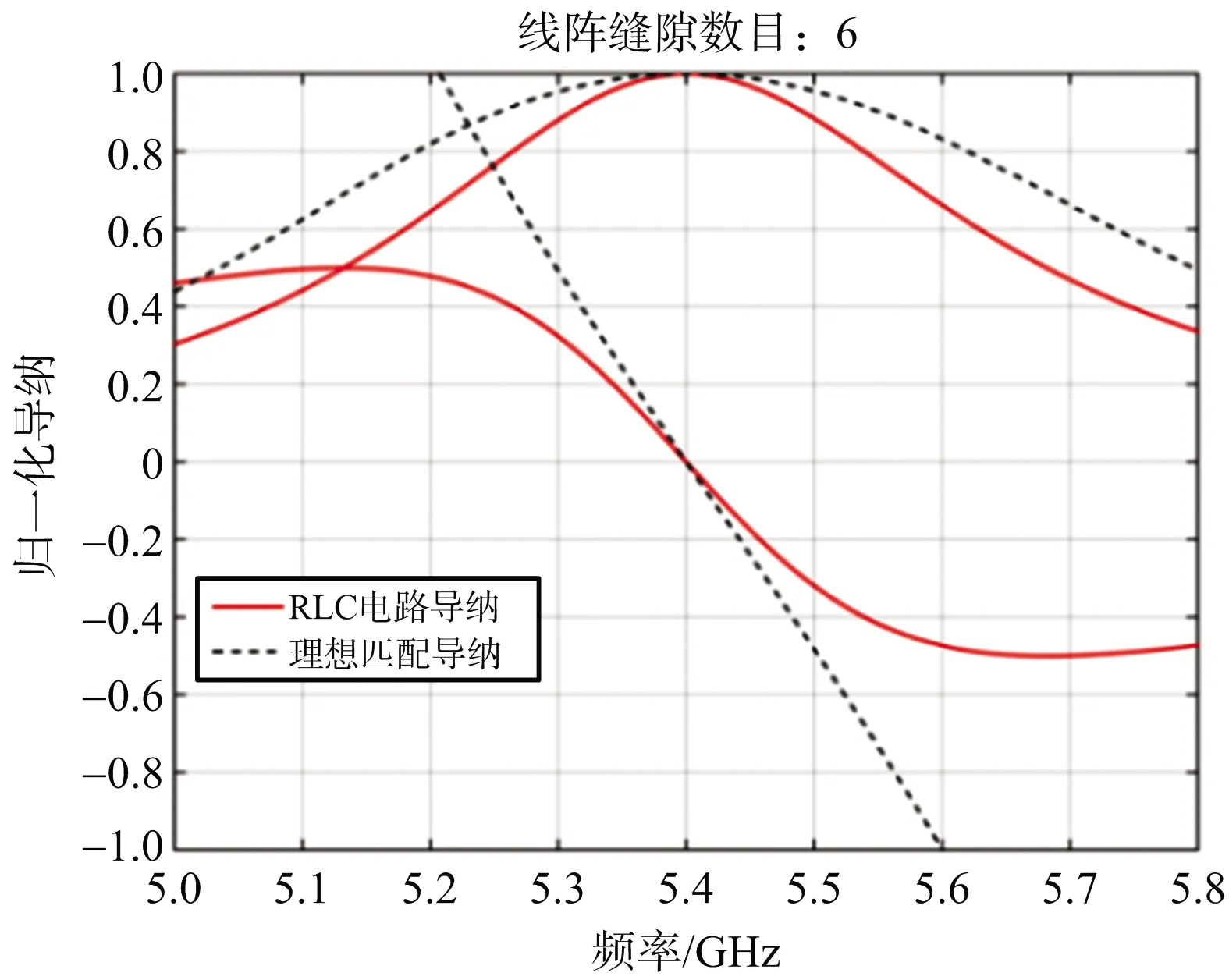
(a) 最大駐波為1.5的導納

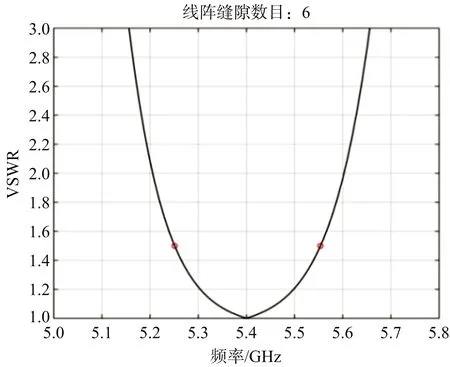
(b) 最大駐波為1.5的帶內駐波

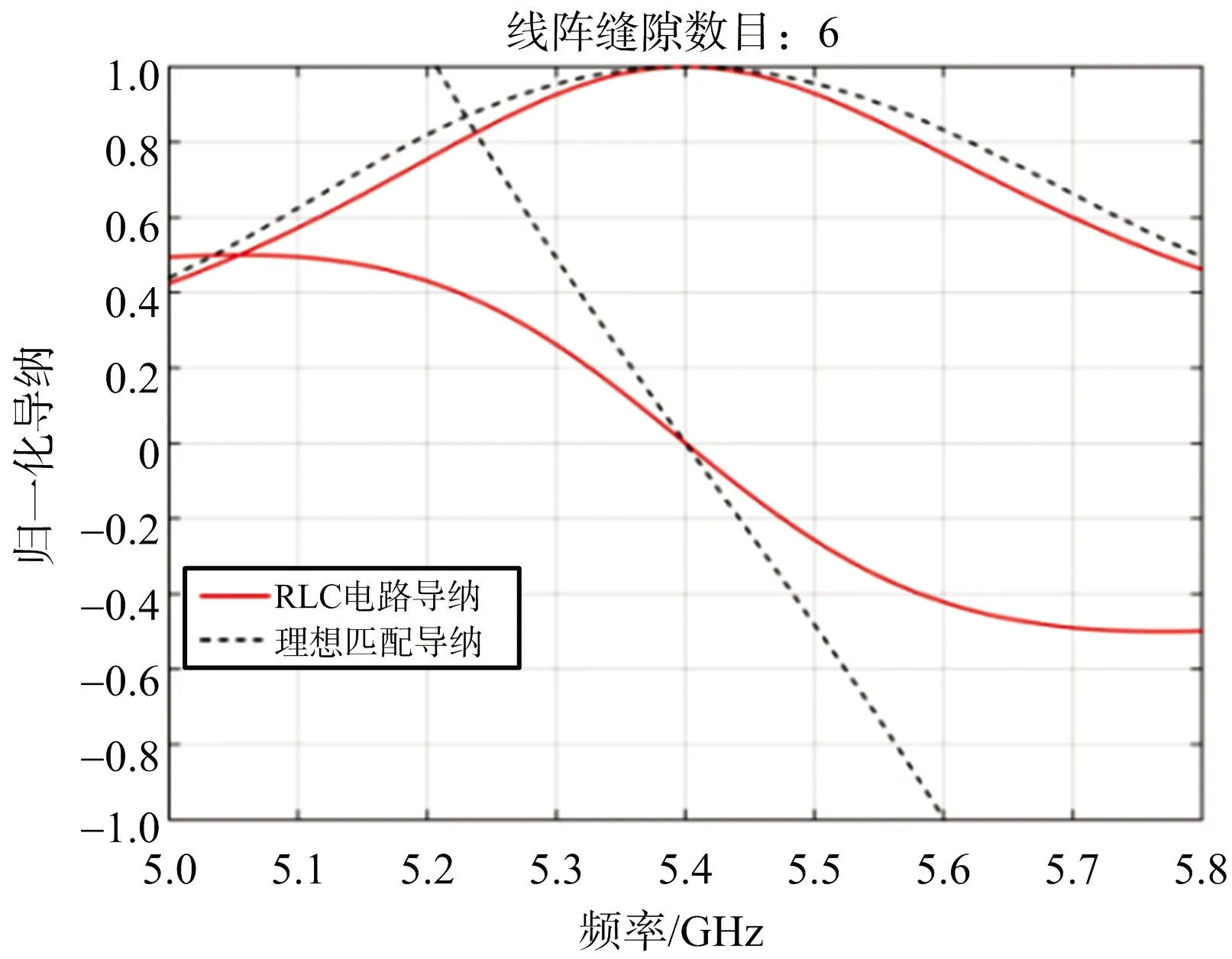
(c) 最大駐波為2.0的導納

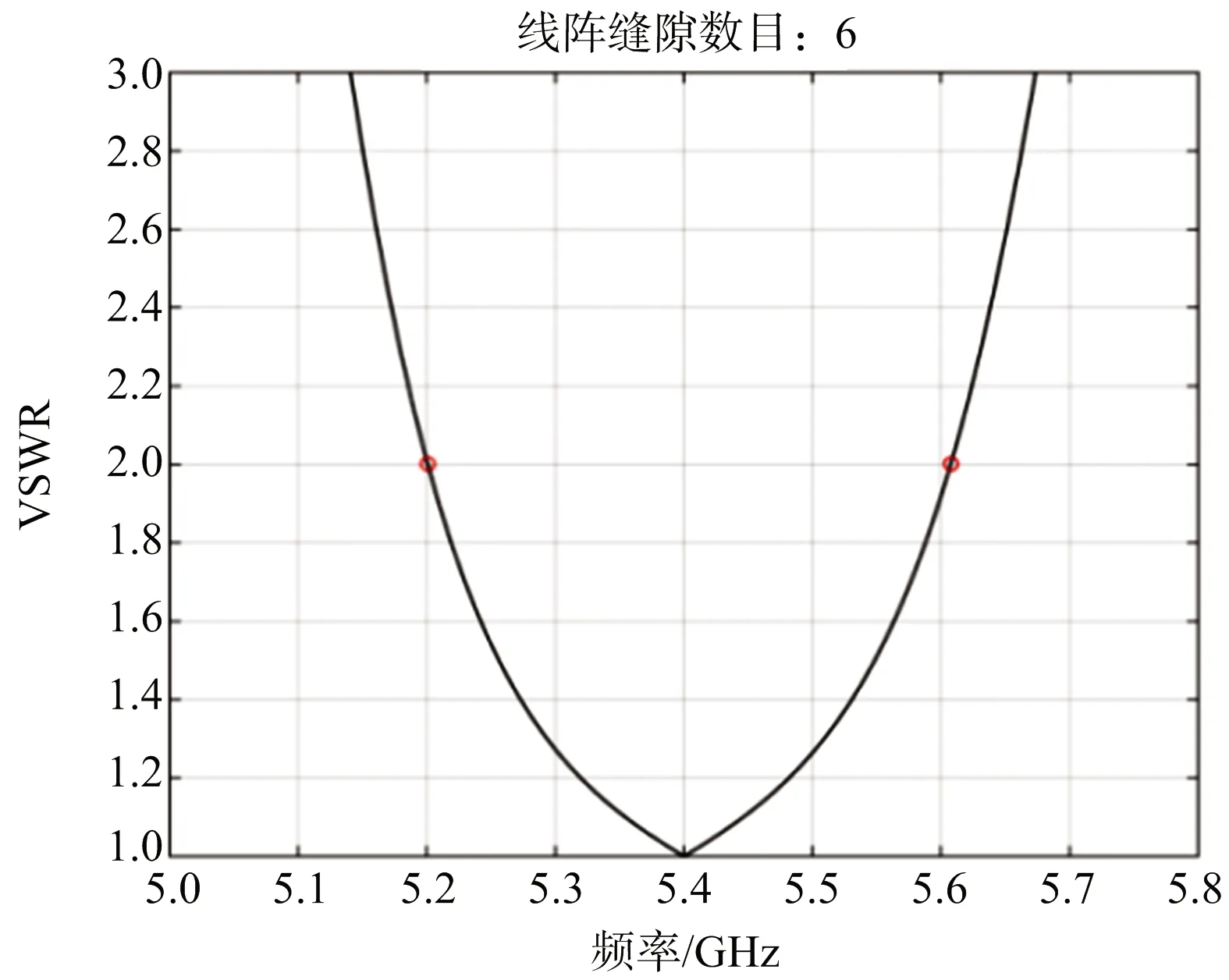
(d) 最大駐波為2.0的帶內駐波圖8 6單元線陣帶寬最優時的導納特性與帶內駐波

2.3 不同單元間距可實現的最大帶寬

由理想匹配條件分析結果，理想導納特性與單元間距相關。對不同單元間距諧振陣的最大帶寬進行分析，并將相同單元間距不同單元數對應的帶寬特性轉化成天線長度(單元數×單元間距)與帶寬的關系曲線，結果如圖9所示。可見，相同諧振陣長度，單元間距越小帶寬越大。這表明在諧振陣長度確定的條件下，為實現最大帶寬，應盡可能選擇小單元間距進行波導諧振陣設計，而不是以縫隙數最少為設計條件。

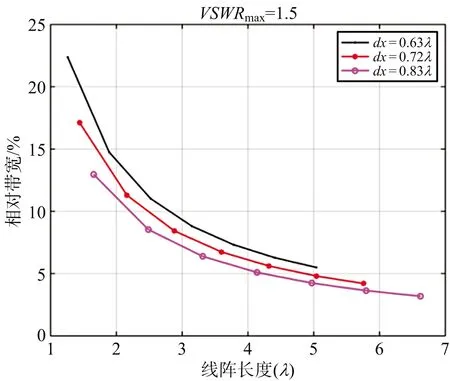
(a) 最大駐波1.5

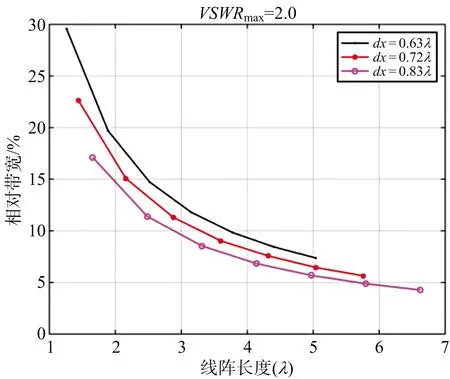
(b) 最大駐波2.0圖9 不同單元間距的線陣長度與帶寬關系

2.4 波導諧振陣最大帶寬的擬合公式

根據并聯縫隙RLC等效電路模型，對不同縫隙數與不同單元間距的最大帶寬進行分析總結，最終獲得了不采用過載技術時波導諧振陣最大阻抗帶寬的通用公式如下：

(9)

式中，bw為百分比最大相對帶寬，λ0為中頻工作波長，dx為縫隙單元間距，N為端饋縫隙陣單元數目。

式(9)考慮了縫隙數與縫隙間距的影響，相對等效電路分析結果，帶寬計算誤差在0.1%以內。

3 矩形波導縫隙寬度對導納特性與帶寬的影響

縫隙波導諧振陣改變縫隙寬度是調整導納的常見方法，下面對縫隙寬度與導納特性的關系進行研究，為天線帶寬的優化設計提供參考。

3.1 縫隙寬度對導納特性的影響

取標準矩形波導寬邊尺寸a=38.55 mm，b=19.28 mm，d=40 mm。各種縫隙寬度情況下的導納特性仿真結果如圖10所示。可見縫隙寬度越寬，歸一化導納變化越平緩，導納的諧振特性越弱。但相比于圖6所示不同縫隙數的諧振陣所需的最優導納特性，縫隙寬度的變化只能在有限范圍內改變導納特性。

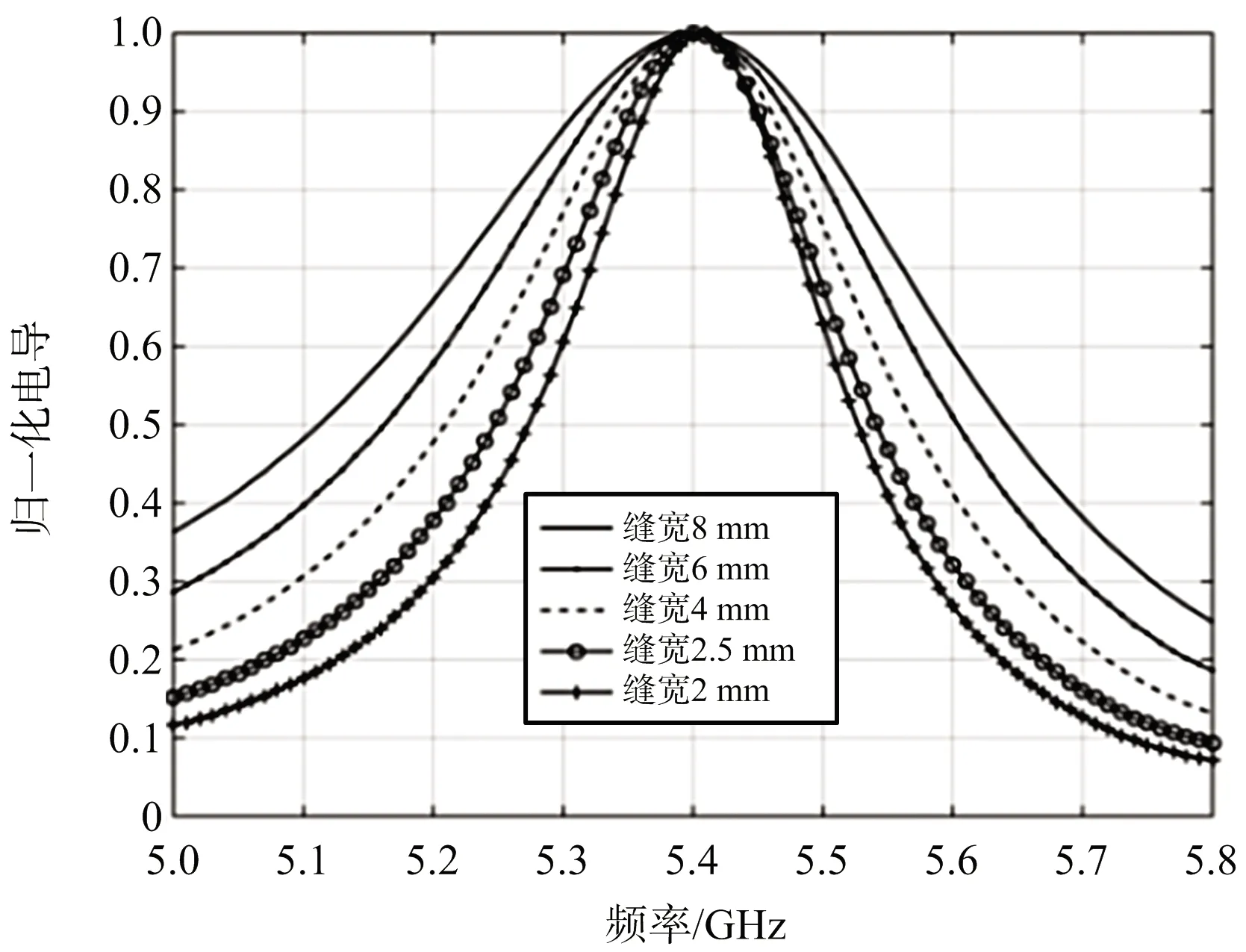
(a) 電導特性

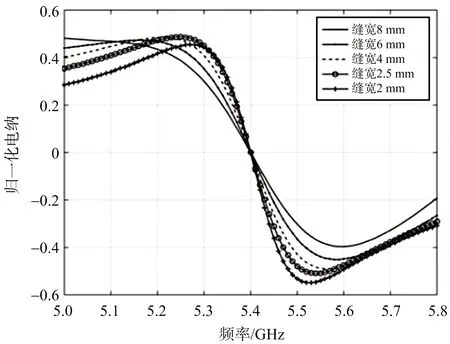
(b) 電納特性圖10 標準矩形波導不同縫隙寬度下的導納特性

3.2 縫隙寬度對阻抗帶寬的影響

為評估縫隙寬度對波導諧振陣帶寬的影響，將計算所得的導納特性代入式(7)，得出縫隙寬度對不同單元數的天線陣的帶內駐波性能和帶寬的影響情況。結果表明，縫隙數≤5時，通過增加縫隙寬度可明顯增加諧振陣的駐波帶寬，但當縫隙數>5時，需要選擇合適的縫隙寬度來實現帶寬的最優化。其中，縫隙寬度對4、8單元線陣端口駐波頻率特性影響的分析結果，如圖11所示。對于4單元陣，單純依靠增加縫隙寬度，即使增加到8 mm，駐波比優于1.5時的最大工作帶寬僅有6.85%，達不到串聯RLC電路所能獲得的8.43%最大工作帶寬。而在單元數為8時，在所分析的幾種縫隙寬度中，寬度為4 mm時駐波比優于1.5的最大帶寬約為4.0%，接近4.2%最大工作帶寬。

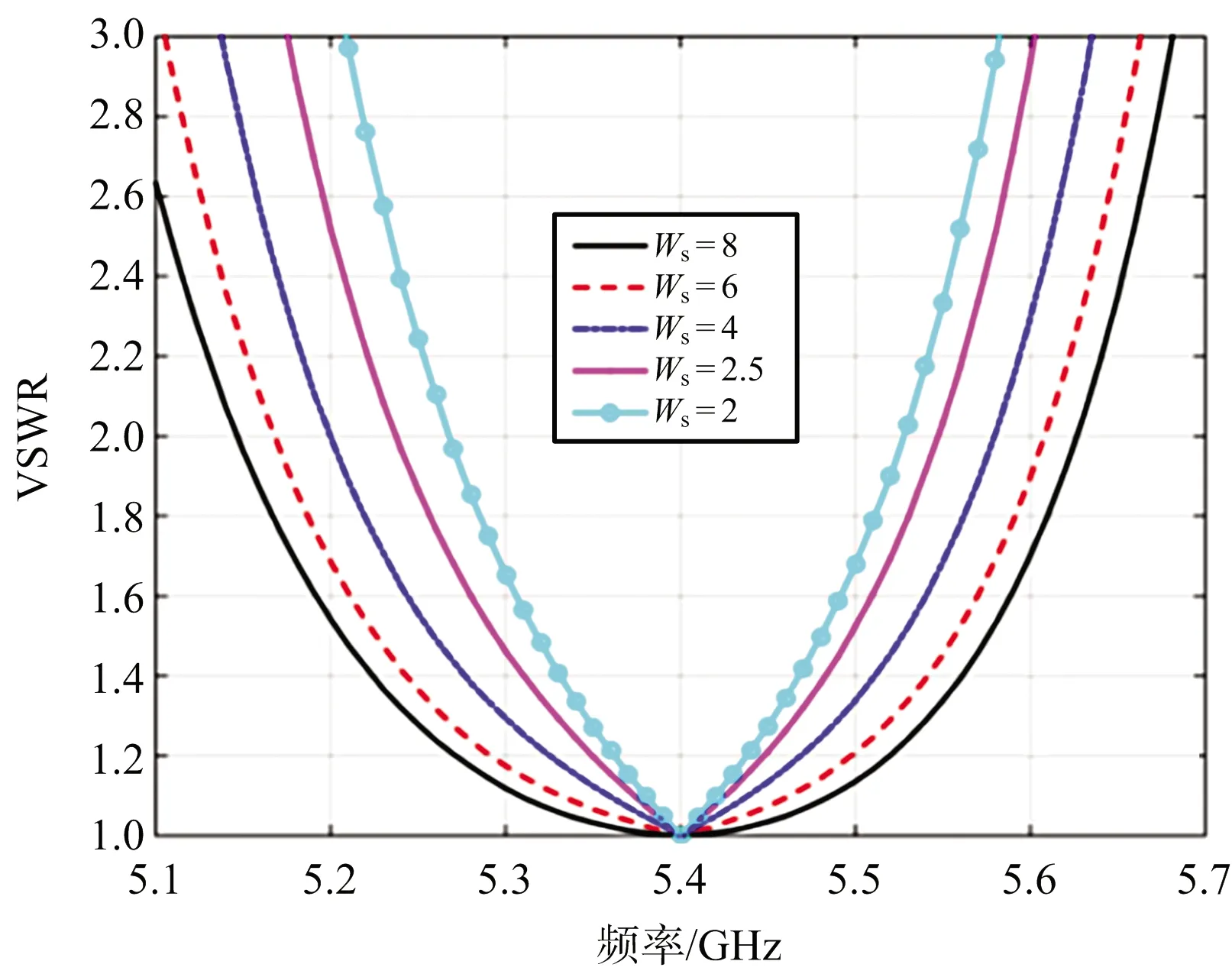
(a) 4單元線陣

可見對于傳統矩形波導縫隙天線，在單元數較少的情況下，單純增加縫隙寬度可展寬工作帶寬，但達不到串聯RLC電路的理論最大帶寬；而在單元數較多時，通過選擇合適的縫隙寬度，可獲得接近理論分析的最大帶寬。

4 設計仿真驗證

為驗證上述分析結果，以8單元端饋波導諧振陣為設計實例，進行天線的全波仿真驗證。此模型采用周期邊界進行設計，其中縫隙間距dx=40 mm=0.72λ0，相鄰線陣間距dy=39.5 mm，最終優化后的縫隙寬度為5.4 mm，縫隙偏置與長度分別為2.68 mm和25.52 mm，具體模型如圖12所示。為補償寬縫隙所引起的電納特性所呈現的感性，在模型中引入了寬邊容性膜片進行調節，膜片高度Wt=1.28 mm。最終的端口駐波特性優化結果如圖13所示，其駐波小于1.5的工作帶寬達到了 4.1%，接近等效電路模型最大帶寬分析結果4.2%，表明并聯縫隙等效電路模型及上述分析結果的正確性。

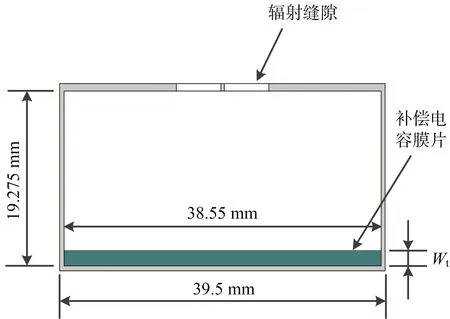
(b) 天線結構參數圖12 8單元線陣周期邊界仿真模型

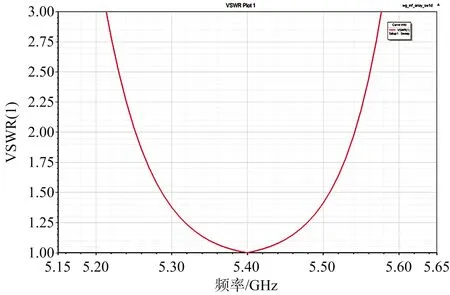
圖13 周期邊界8單元線陣端口駐波全波仿真結果

5 結束語

本文利用傳輸線理論，給出了不同單元數、單元間距及縫隙寬度的波導諧振陣實現理想匹配時的導納頻率特性曲線，為后續尋求縫隙諧振陣的全帶寬阻抗匹配設計提供了參考。提出了并聯縫隙的RLC串聯等效電路模型，用單參數串聯電容C實現了對縫隙導納特性的表征，據此建立了分析縫隙波導諧振陣阻抗帶寬的新方法，獲得了諧振陣實現阻抗帶寬最優化所需的導納特性曲線，為常規波導諧振陣工作帶寬的最大化設計確定了導納優化目標。總結了諧振陣不采用過載技術時，計入單元數與單元間距影響下的最大阻抗帶寬的通用公式。并由此得出在波導長度固定的情況下，選擇小單元間距有利于增加阻抗工作帶寬的結論，為波導諧振陣的布陣優化提供了帶寬方面的設計依據。

以標準矩形波導諧振陣為例，研究了縫隙寬度對導納特性和工作帶寬的影響情況，結果表明縫隙寬度可對縫隙導納特性進行有限范圍的調整，在縫隙數較少時，可通過增加縫隙寬度有效提高阻抗帶寬，但難以達到RLC電路的理想最大工作帶寬；而當縫隙數較多時，可通過選擇適當的縫隙寬度實現帶寬的最大化。最后，利用全波仿真軟件進行了8單元線陣帶寬的優化設計，仿真與理論分析結果基本吻合，證明了分析方法和設計過程的有效性。

本文提出的阻抗帶寬分析方法，為波導諧振陣帶寬的精確設計提供了一種有效手段，具有很好的工程參考價值。后續我們將用此方法對過載技術進行研究，探索采用過載技術時諧振陣的帶寬上限。同時還將對不依賴于縫隙寬度變化實現縫隙導納有效調整的方法進行研究，以實現不同縫隙數的波導諧振陣阻抗帶寬的最優化設計。