復合煤層露天礦多采區配采推進度模型優化

劉光偉，張 靖，于秋宇，宋佳琛，董瑞榮

（1.遼寧工程技術大學 礦業學院，遼寧 阜新 123000；2.華能伊敏煤電有限責任公司，內蒙古 呼倫貝爾 021134；3.內蒙古霍林河露天煤業股份有限公司，內蒙古 通遼 028000）

我國煤炭資源豐富，但地質條件復雜程度高[1]，隨著我國對安全和環保的不斷重視，以及露天開采安全高效環保的特點，其在煤炭資源開采中所占比例越來越高[2-3]。在露天開采過程中，采區的推進度過小，使工作線長度過長，運距過大，推進度過大，使膠帶移設步距過大。因此，合理推進度的確定一直都是露天礦生產的關鍵問題[4-5]。霍林河南露天礦境界形狀復雜，且有多種采排工藝并存，經過多年的發展，現有南采區、北采區和配采區并行開采。隨著礦山工程的發展，只有南內排和中內排能夠釋放內排空間，內排空間不足，采排接續困難；南采區面臨到界問題，將急劇釋放內排空間，而在后期的開采過程中，因受工作線長度的變化、運輸連接橋拆除、采剝工程降深等因素影響，間歇性遇到剝離洪峰，造成內排空間釋放與剝離量產生在時空上不能較好地匹配，會形成多采區并行開采的情況，這種復合煤層露天礦多采區配采的問題是露天開采理論中的重點問題之一。

隨著技術水平的提高，可以通過數字化建模的方法解決礦山在開采過程中的相關問題[6-7]。對于復雜地質問題，武強等[8-9]根據斷層的基本屬性，運用單一平面或者多個平面擬合斷層面的方式，推演未知斷點，對斷層的空間幾何形態進行數學描述，并且提出了基于體分割的層次三維拓撲結構和基于面向對象的框架模型，同時結合礦山數據特點及數字礦山建設目標，提出了多源數據耦合、多種構模方法集成、多分辨率可視化與檢測以及多維數據分析與應用的理論體系，針對建模流程各環節中不確定性等問題進行了分析，實現了復雜地質構模、資源儲量模擬評價和采掘工程開挖等關鍵技術方法，隨著礦山勘探、開發和復墾等進程的推進，三維地質建模歷經“構建-模擬-修正”的動態更新與完善過程；朱良峰等[10-11]全面而系統地研究了地質斷層三維可視化構模的原理、方法及實施過程，針對地質斷層三維構模的特點與要求，設計了一種基于邊界表示、面向地質實體并兼顧拓撲關系的三維數據模型，以有效地組織和描述包含斷層的復雜地質體幾何結構模型，提出了斷層與地層的統一構模技術，并解決了在其實現過程中所遇到的問題，同時基于基礎GIS 軟件平臺MAPGIS，利用功能強大的三維可視化開發平臺MAPGIS-TDE，設計、開發具有自主版權的三維地質建模及可視化系統；查振高等[12]根據影響采區接續的主要因素，選取了生產剝采比穩定性與大小、累計剝采比、內排空間、采區協調性和運輸功5 個指標建立了露天礦采區接續優選指標體系，構建了基于Delphi-TOPSIS 法的采區接續優選模型，針對霍林河露天煤礦采區劃分特點，提出了采區接續方案并采用Delphi-TOPSIS 模型進行優選，確定了最佳采區接續轉向方案并證明了方法的準確性；劉桐等[13]研究了霍林河南露天礦的采區劃分和開采順序問題，優化了采區劃分方式和開采程序，基于模糊數學方法的采區過渡方式優選模型，結合采區劃分與開采順序優化結果，確定了緩幫方式，針對南礦南采區過渡優化研究，論分析了南采區過渡閉坑期間面臨的問題；王威欽等[14]為解決煤層群合理配采的需求及對煤質穩定的要求，分析了煤層賦存條件和開采方式對各煤層生產原煤煤質灰分的影響，通過大量地質鉆孔統計，分盤區分析計算了現有綜采條件下各煤層的煤質灰分預測值，得出配采灰分，為煤層群配采提供參考依據，根據礦井開拓和發展規劃，按照合理錯距，設計出合理的工作面配采方案，達到為選煤廠按優化配采方案提供均質原煤的目的；曹蘭柱等[15]為探究弱層賦存位置及形態對復合煤層露天礦邊坡滑坡模式的影響，采用剩余推力法與FLAC3D數值模擬法，結合露天礦采場自上而下逐水平形成的特點，提出一種新的復合煤層露天礦邊坡參數逐階段優化方法，將該方法應用于霍林河南露天礦，分3個階段優化設計了該礦頂幫復合煤層邊坡空間形態，避免了霍林河南露天礦頂幫未降深至坑底時就沿17 煤底板弱層發生滑坡；徐勇超等[16]基于如何能夠在設計及實際生產組織過程中優化運距，減少柴油成本，對整個煤業的節支降耗、壓降成本、對標管理及利潤增長都具有相當重大的意義，從配采區與三采區之間的“鼻梁”道，一號礦礦內排運輸系統的優化，以及二號礦一、二采區驗收房改造這3 個方面進行分析與討論，以此對整個煤業生產和壓降成本產生積極的影響。專家學者們的研究成果對于解決復合煤層露天礦問題有重要的指導意義，但目前在露天礦多采區配采方面的研究成果較少，尤其是針對復雜地質條件下復合煤層的露天礦。

當開采煤層的數量多、地質構造的復雜程度高且多采區同時開采時，簡單的數學計算無法滿足生產規劃需求，若要滿足產能，剝采比等要求，構建符合實際的數學模型至關重要。為此，在其他學者研究的基礎之上[17-18]，針對復雜地質條件下的露天礦多采區配采問題展開研究，并通過模擬開采構建多采區推進度數學模型，以數學模型為露天礦的采區發展規劃理論基礎。

1 霍林河南露天礦概況

霍林河南露天礦斷層多，煤層為復合煤層，開采煤層數多，傾角變化大且構造發育，個別煤層局部發育，并非全區發育，可采煤層共計9 層，為6、8、10、11、14、17、19、21、24 煤層，其中14、17、19、21 為主要可采煤層；煤層傾角大，約為5°～15°，向斜兩翼傾角不一。斷層數量多，落差較大，而且相互切削。

霍林河南露天礦為大型生產礦山，最新產能核定為18 Mt/a。經過多年發展以及當時歷史局限性，現有3 個采區并行開采，分別是南采區、北采區和配采區。

按照現有工作線布置方式，南采區工作線東西布置，向北推進；北采區和配采區工作線南北向布置，向西推進。采區發展方式示意圖如圖1。

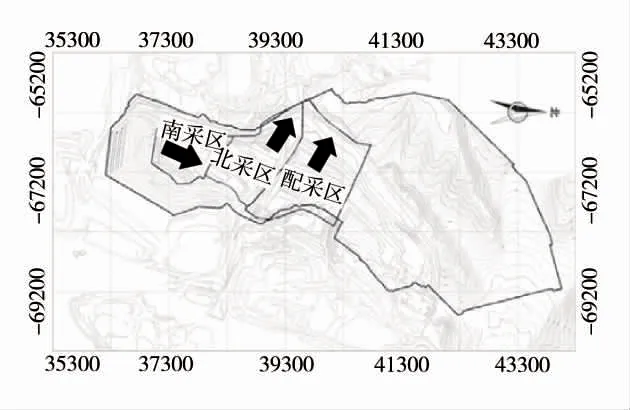
圖1 采區發展方式示意圖

2 采區模擬開采與回歸分析

霍林河南露天礦煤層數量多，煤層厚度變化較大，在露天開采過程中，由于斷層的影響，采剝量往往會發生較為劇烈的變化。當變化較為劇烈時，原有的通過工作線長度和煤層厚度確定采剝量的方法無法精確反映工作幫推進過程中采剝量的變化規律。因此，采用模擬開采與回歸分析的方法，研究露天礦中采剝量隨推進距離的變化規律，分別對各個采區發展變化規律進行研究（研究露天礦中各個采區的采剝量隨推進距離的發展變化規律）。為了表示模擬開采過程的連續性，采用累積采煤量、累積剝離量和剝采比表示模擬開采中各階段的采剝情況，并通過曲線擬合的方法構建采區發展的數學模型。

南采區的南幫和東幫已經形成內排臺階，推進方向為由南向北，南采區范圍內主要開采17 煤和21 煤，局部區域存在19 煤，主要剝離物為17 煤與21 煤之間的夾矸。南采區17 煤以上覆巖已經全部完成剝離，且已露出17 煤頂板。南采區范圍內剩余煤量990 萬t，剝離量1 054 萬m3，平均剝采比為1.06 m3/t，整體剝采比較小。

以工作平盤寬度60 m，臺階坡面角70°，臺階高度12 m 為開采參數創建工作幫推進模板，采區按照步距60 m 沿工作線推進方向推進，對累積采煤量和累積剝離量與推進距離的關系進行函數擬合。南采區逐階段累積采煤和剝離量見表1，南采區逐階段累積采煤和剝離量散點圖如圖2。

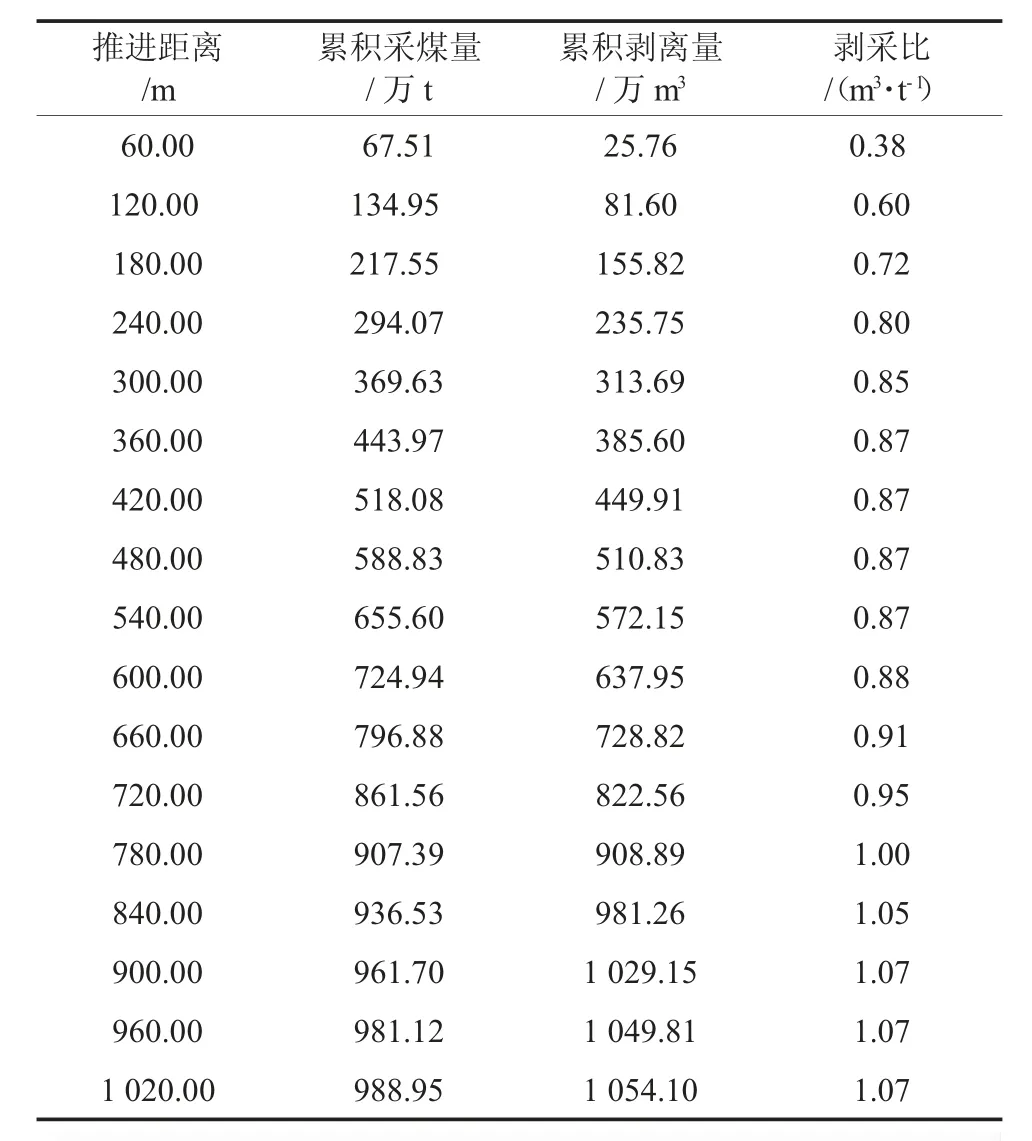
表1 南采區逐階段累積采煤和剝離量

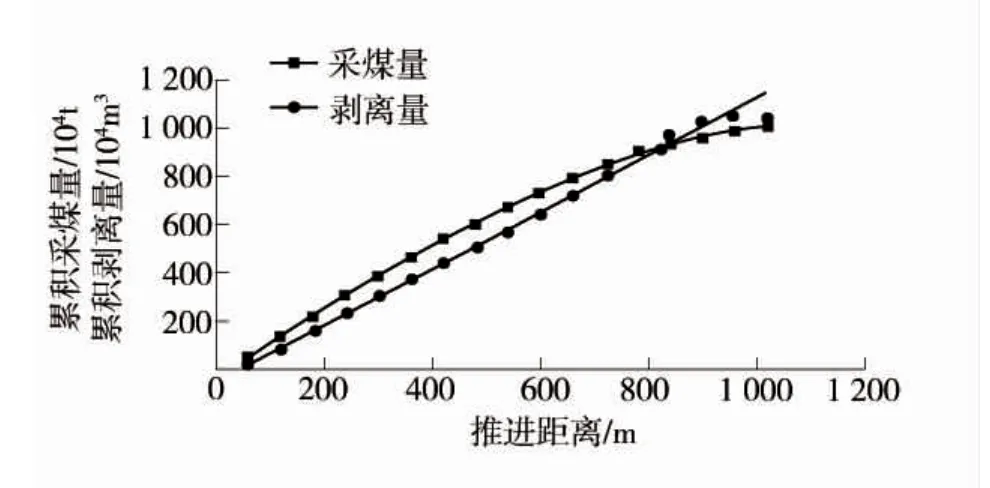
圖2 南采區逐階段累積采煤和剝離量散點圖

隨著南采區由南向北推進，采煤量和剝離量總體呈上升趨勢，到后期趨于平緩，原因是采區即將到界之時工作幫靠幫到界，采煤量和剝離量逐漸減少。將工程位置與工程量用散點圖擬合出的線性方程來描述，累計剝離量和采煤量均近似符合一次多項式的分布，故采用一次函數對累積采煤量和累積剝離量進行曲線擬合，擬合度分別為R2=0.995 6 和R2=0.984 3，較為接近1，表明對于南采區推進距離與累積采煤量和剝離量的回歸分析較為可靠。

北采區的推進方向為由東向西，北采區范圍內主要開采10 煤、14 煤、17 煤和21 煤，局部區域存在6 煤、8 煤、11 煤和六號路下的24 煤，主要剝離物為各層煤之間的夾矸。北采區內剩余煤量2 709 萬t，剝離量10 263 萬m3，采區范圍內平均剝采比為3.62 m3/t，整體剝采比大于目標剝采比3.4 m3/t。北采區與南采區以Fd17斷層為界，北采區與配采區以六號路為界。為了實現3.4 m3/t 的優化目標，需要研究北采區剝采比的變化情況。

按照與南采區相同的方法對北采區進行模擬開采，并根據模擬開采得出的數據進行回歸分析與曲線擬合，計算出模擬開采逐階段累積量。北采區逐階段累積采煤和剝離量見表2，北采區逐階段累積采煤和剝離量散點圖圖如圖3。

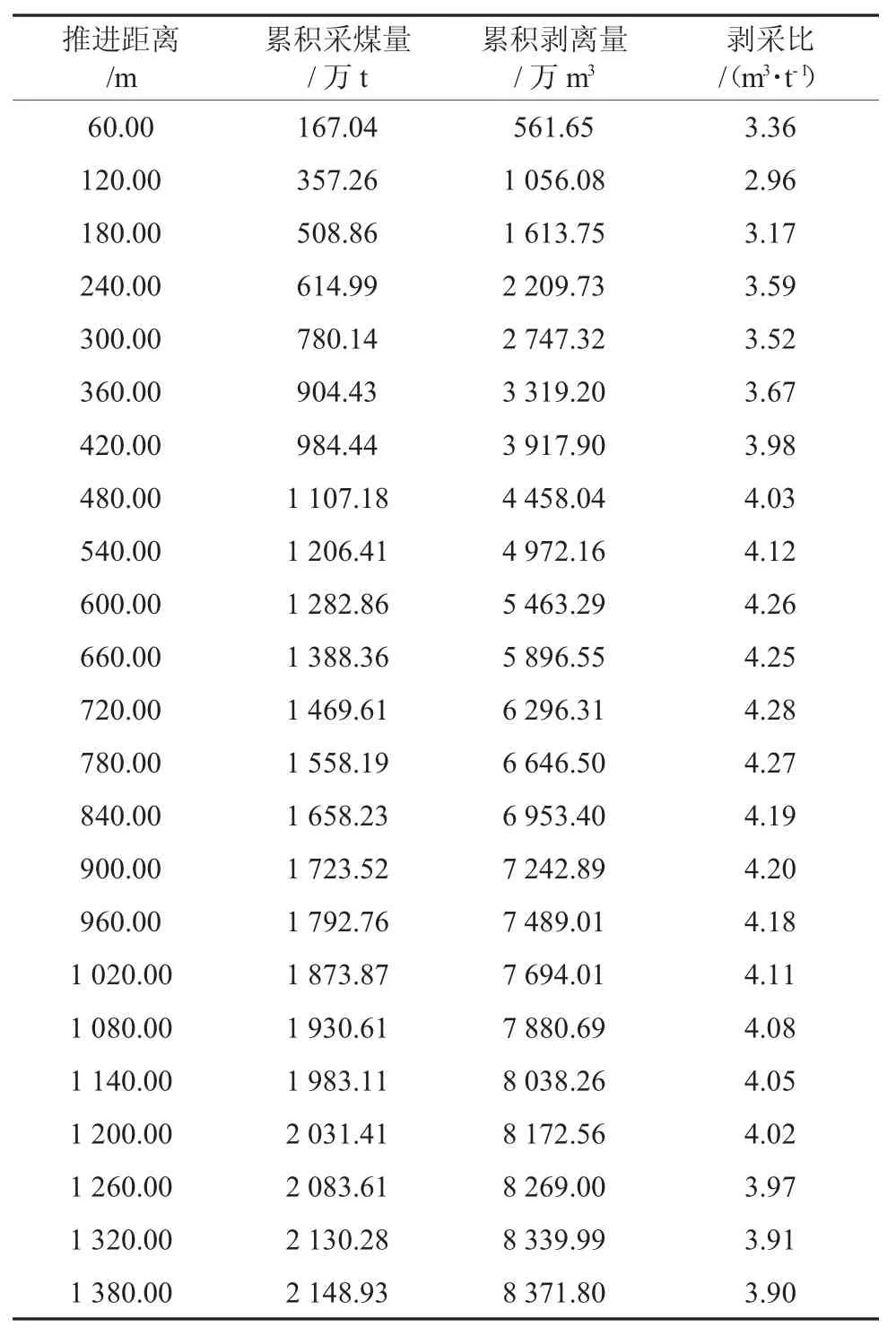
表2 北采區逐階段累積采煤和剝離量

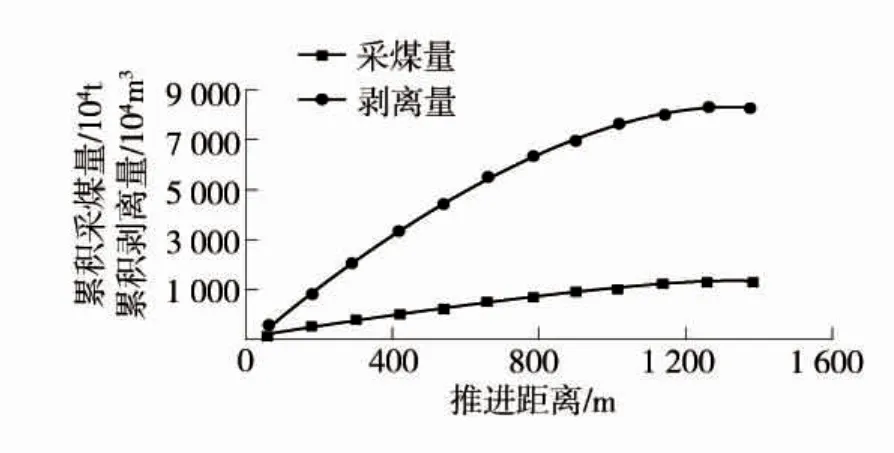
圖3 北采區逐階段累積采煤和剝離量散點圖

北采區累積采煤量和剝離量分別符合一次多項式和二次多項式的分布，累積采煤量和累計剝離量分別采用一次函數和二次函數擬合，擬合度分別為R2=0.999 2 和R2=0.999，擬合度較為接近1，表明對于北采區推進距離與累積采煤量和剝離量的回歸分析較為可靠。

配采區的東部已經露出21 煤底板，但尚未形成內排土場，推進方向既可以由東向西縱采推進，也可以由南向北橫采推進。配采區范圍內主要開采10煤、14 煤、17 煤和21 煤，局部區域存在11 煤和24煤，主要剝離物為各層煤之間的夾矸以及西部的表土。配采區內剩余煤量約6 994 萬t，剝離量約17 249 萬m3，采區范圍內平均剝采比為2.47 m3/t。

按照與南采區相同的方法對配采區進行模擬開采，并根據模擬開采得出的數據進行回歸分析與曲線擬合，計算出模擬開采逐階段累積量。配采區逐階段累積采煤和剝離量見表3，配采區逐階段累積采煤和剝離量散點圖如圖4。

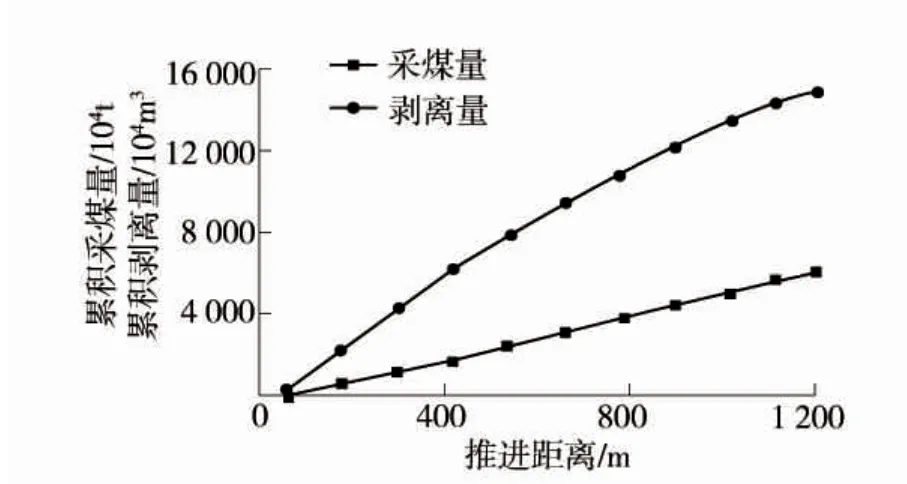
圖4 配采區逐階段累積采煤和剝離量散點圖

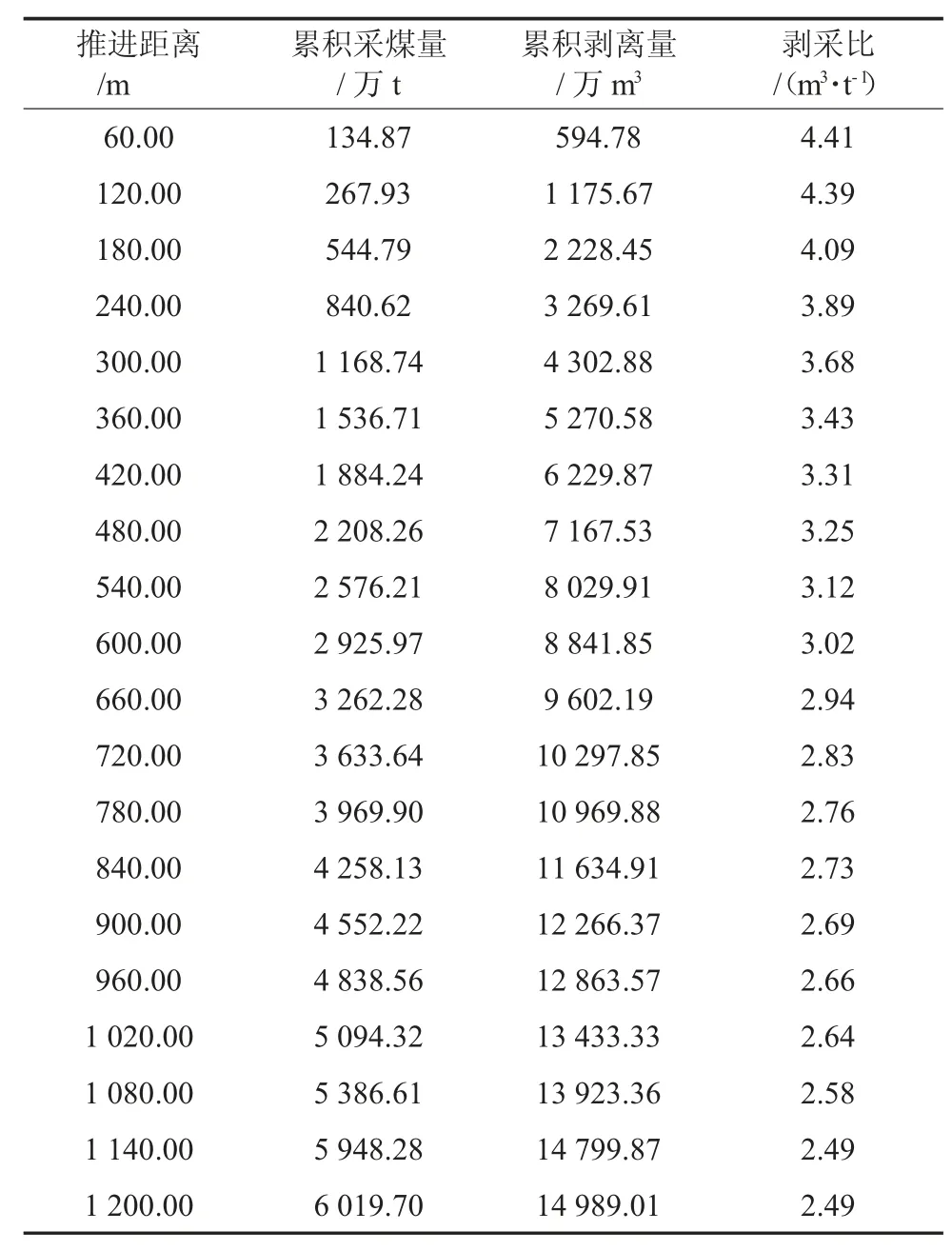
表3 配采區逐階段累積采煤和剝離量

配采區由東向西縱采推進，累積采煤量和累積剝離量分別符合一次多項式和二次多項式分布，故采用一次函數和二次函數對累積采煤量和累積剝離量進行曲線擬合，擬合度分別為R2=0.998 8 和R2=0.999 9，較為接近1，表明對于配采區縱采推進距離與累積采煤量和累積剝離量的回歸分析較為可靠。

通過表1、表2、表3 中推進距離與剝采比之間的關系，得出各個采區的剝采比變化情況，各采區剝采比變化散點圖如圖5。

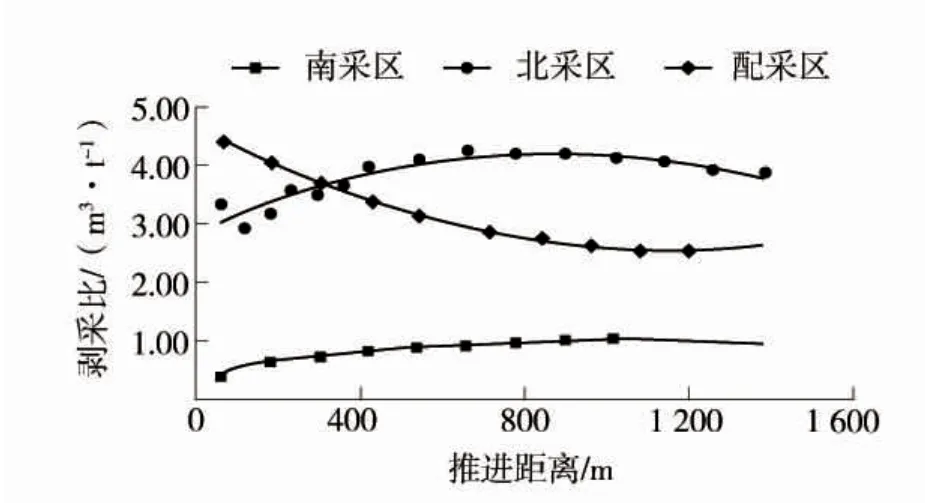
圖5 各采區剝采比變化散點圖

各采區累積采煤量和剝離量采用二次函數進行曲線擬合，擬合度分別為R2=0.925 5，R2=0.884 6 和R2=0.989，較為接近1，表明對于各采區縱采推進距離與累積采煤量和剝離量的回歸分析較為可靠。

3 多采區推進度模型

根據對霍林河南露天礦3 個采區的模擬開采，分析各采區采剝量與推進距離之前的變化趨勢，對變化趨勢進行函數擬合，各個采區的采煤量A′、剝離量Vs與推進距離l 之間的函數關系如下：

1）南采區采剝量與推進距離之前的關系。

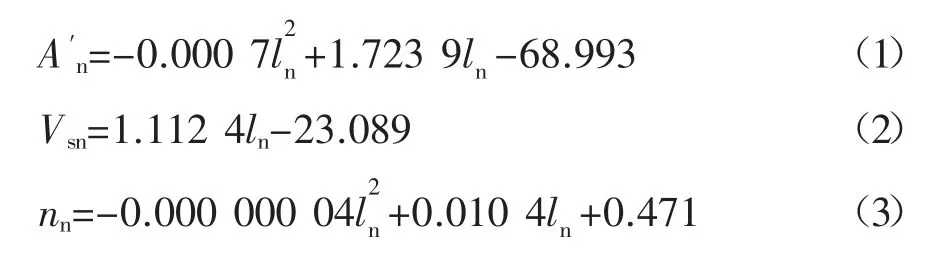
2）北采區采剝量與推進距離之前的關系。

3）配采區采剝量與推進距離之前的關系。

各采區空間發展時，剝離量、采煤量的函數關系建立后，根據礦區的采煤量、剝離量和剝采比等約束條件構建3 個采區間的推進度函數關系。按照采煤量18 Mt/a、剝離量61.20 Mm3/a、剝采比n=3.4 m3/t為約束條件，構建南采區、北采區和配采區的推進度函數關系模型。

將式（1）～式（10）聯立得式（11）：

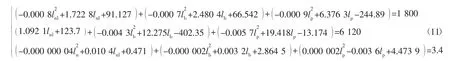
式（1）為滿足年采剝量和剝采比的3 個采區年推進度的數學模型。

由于式（11）方程組，通過手工方法進行求解過于復雜，錯誤率高，而且MATLAB 軟件具有高效的數值計算功能，能將繁雜的數學運算以簡單方法計算出來，對工程中的數學問題求解有廣泛的應用[19]，因此，用MATLAB 軟件進行求解。

求得的8 組解中只有2 組為實根，其中第5 組解為負根，由于推進度不能為負值，所以只能取第6組解為3 個采區推進度的最終解，即當3 個采區年推進度為ln=395.19 m、lb=218.98 m、lp=253.54 m，可以滿足采煤量指標、剝離量指標和剝采比約束。

4 結語

1）根據對霍林河南露天礦3 個采區的模擬開采，分析各采區采剝量與推進距離之間的變化趨勢，對變化趨勢進行函數擬合，以生產指標中的采煤量、剝離量和剝采比為約束條件，構建3 個采區推進度之間的數學模型，得出了南采區、北采區、配采區的剩余煤量和剝離量，進而得出平均剝采比，均符合目標剝采比的要求。

2）根據三采區模擬開采得出的累計剝采量表，南采區、北采區、配采區均采用一次函數或二次函數分別對累積采煤量和累積剝離量進行曲線擬合，擬合度均接近于1，表明對于各采區縱采推進距離與累積采煤量和剝離量的回歸分析較為可靠。

3）通過MATLAB 進行模型求解，通過對多組解進行比較取舍，確定了3 個采區年推進度為ln=395.19 m、lb=218.98 m、lp=253.54 m，可以滿足采煤量指標、剝離量指標和剝采比約束。