吉林一號寬幅01星寬幅相機在軌幾何定標及精度驗證

武紅宇，白 楊，王靈麗，張 雷，王 棟，巴倩倩，賈 益，鐘 興

（長光衛星技術有限公司，吉林 長春 130000）

1 引 言

2020年1月15日，吉 林 一 號 寬 幅01星（Ji‐lin1-KF01A）在太原衛星發射中心通過長征二號丁運載火箭成功發射。Jilin1-KF01A亞米級寬幅相機采用大口徑、大視場、長焦距的離軸三反式光學系統設計，可獲取全色分辨率0.75 m、多光譜分辨率3 m、幅寬優于136 km的推掃影像，是全球目前幅寬最大的亞米級光學遙感衛星，具有高分辨率、超大幅寬、高速數據傳輸的特點。Ji‐lin1-KF01A的成功發射標志著我國民用商業衛星的飛躍，對大范圍地球觀測具有獨特優勢。

高精度幾何定位是發揮高分辨率衛星性能和價值的基礎［1］，在軌幾何定標是提升高分辨率遙感衛星幾何性能的重要環節，同時也是衛星幾何校正處理的必要步驟［2］。Jilin1-KF01A發射前對星上載荷進行了嚴格的實驗室檢校，線陣相機二維高精度內方位元素標定方法已將重投影誤差提升至0.34 pixel［3］，但是由于衛星發射及衛星入軌后環境等因素的影響，星上測量器件的狀態發生了改變，使得實驗室檢校參數無法表征衛星在軌的真實狀態，從而導致光學影像的幾何定位精度下降。因此，通過攝影測量方法對成像系統的內外方位元素進行精確標定，從而為影像幾何處理提供精確的幾何成像參數是光學遙感影像高精度幾何處理的關鍵［1］。

歐美航天強國積累了豐富的在軌幾何定標經驗，法國SPOT衛星經過在軌幾何定標后的無控定位精度達到了50 m［4］，美國IKONOS衛星經過在軌幾何定標后的無控定位精度達到了12 m［5］，Geoeye-1以 及WorldView-1-3的 無控 定位精度均優于4 m［6-8］。國內相關研究起步較晚，但在國家“高分專項”等項目的支持下，我國遙感衛星在軌幾何定標技術得到了迅速發展。楊博等針對資源一號02C衛星全色相機進行了在軌幾何定標，其無控定位精度從定標前的1 500 m提升到了定標后的100 m左右［8］。蔣永華等針對我國第一顆民用測繪衛星資源三號進行了在軌幾何定標，定標后其無控定位精度優于20 m［10］。王密等對高分四號靜止軌道衛星進行了在軌幾何定標，經過幾何定標后可見光近紅外傳感器與中紅外傳感器的內部畸變在沿軌與垂軌方向上均穩定優于1個像元［11］。王密等對高分五號可見短波紅外高光譜影像進行了在軌幾何定標，定標后其無控定位精度提升到了60 m，內部精度優于0.5像元，波段配準精度優于0.3像元［12］。王密等對高分六號寬幅相機進行了在軌幾何定標及精度驗證，結果表明其絕對定位精度在3像元左右，內部幾何精度能穩定在1像元，譜段間配準精度在0.3像元以內［13］。

Jilin1-KF01A的亞米級寬幅相機的焦平面采用超多片線陣TDI CCD機械交錯拼接，成像幅寬達到了136 km，TDI CCD品字型偏視場設計使得相機對地成像時同一時間獲取的超多片影像不共線，相鄰TDI CCD間獲取的相同地物的影像具有一定的時間差，并且是在衛星處于不同位置、時間、姿態及視角下獲取的，因此上述在軌幾何定標方法難以直接應用。本文在現有幾何定標研究的基礎上，根據Jilin1-KF01A亞米級寬幅相機的成像特點，將探測器按單景影像23 km幅寬分為6組進行在軌幾何定標，將定標系數分解為內方位元素定標參數與外方位定標參數，并結合大幅寬超多片探測器機械交錯拼接相機的成像特點，采用附帶片間幾何定位一致性約束的分步迭代法求解定標系數，最后利用真實數據進行了在軌幾何定標實驗，驗證了方法的可行性。目前，定標參數已實際應用在Jilin1-KF01A亞米級寬幅相機L1級標準數據產品的生產系統中。

2 在軌幾何定標模型與方法

亞米級寬幅相機是Jilin1-KF01A上的主要載荷，表1列出了亞米級寬幅相機的具體信息。

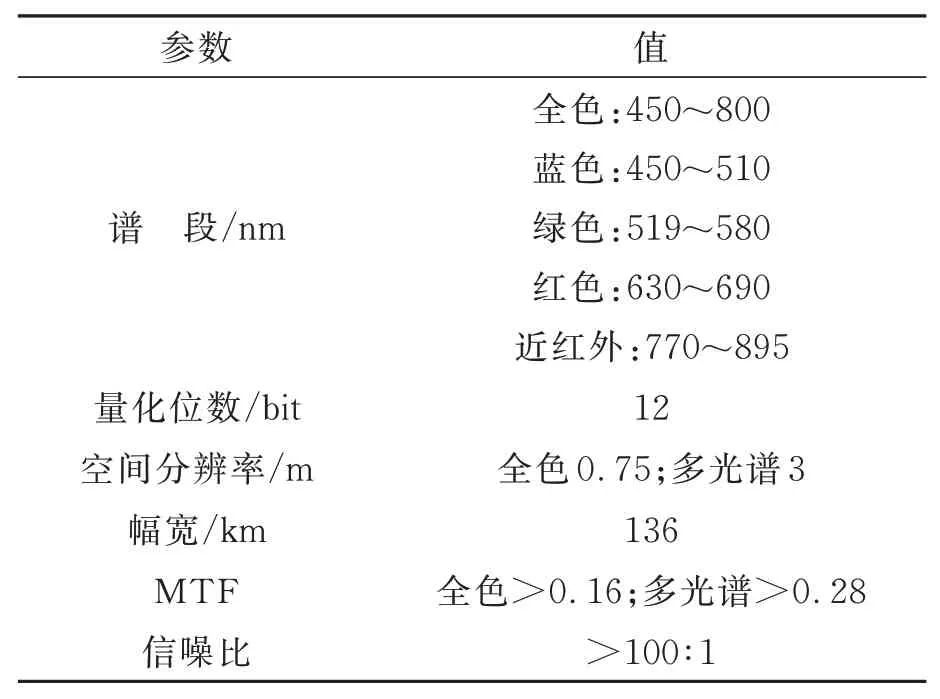
表1 吉林一號寬幅01星寬幅相機的主要參數Tab.1 Main performance of wide-field-of-view camera on Jilin1-KF01A

2.1 亞米級寬幅相機在軌幾何定標模型

Jilin1-KF01A采用線陣推掃方式成像，其嚴密成像幾何模型符合中心投影成像共線方程，因此以共線方程為基礎，依據光學衛星推掃成像原理［14］，同時結合衛星成像過程中的GPS測量數據、衛星成像姿態測量數據等輔助數據構建了嚴密成像幾何模型，即：

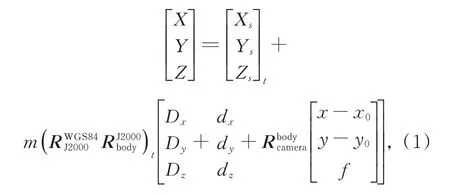
其中：[Xs Ys Zs]tT是t時刻GPS相位中心在WGS84坐標系下的位置矢量，是t時 刻J2000坐標系到WGS84坐標系的旋轉矩陣，(RJ2000body)t是t時刻衛星本體坐標系到J2000坐標系的旋轉矩陣，[Dx Dy Dz]T是GPS相位中心在衛星本體坐標系下的坐標，[dx dy dz]T是相機坐標系原點相對于衛星本體坐標系的平移，是相機坐標系到衛星本體坐標系的旋轉矩陣，[x-x0y-y0-f]T中(x y)T是當前像點坐標，(x0y0)T對應的相機主點坐標，f是相機主距。最后得到的[X Y Z]T是當前像點坐標(x y)T在WGS84坐標系下的位置矢量。

推掃式光學衛星在成像過程始終處于運動狀態，且Jilin1-KF01A的亞米級寬幅相機成像鏈路較為復雜，其中的幾何誤差種類多，主要包括相機安裝誤差、時間測量誤差、衛星姿態觀測誤差、GPS觀測誤差、GPS偏心誤差、相機內部畸變造成的像點誤差以及衛星動態運動成像過程中引入的隨機誤差。現有研究表明，這些誤差難以完全剝離，可將在軌幾何定標分為外方位元素定標和內方位元素定標［14］。在軌幾何定標的目的是通過標定成像模型中的系統誤差提升衛星獲取影像數據的幾何定位精度。上述誤差中，姿態觀測誤差和GPS觀測誤差中既有系統誤差，如星敏觀測常角誤差，也有隨機誤差，如星敏觀測噪聲等。隨機誤差無法通過建立模型進行消除，通常可采用高精度測量器件來提高測量精度，各器件的時間測量誤差可通過GPS統一高精度授時來減小。Jilin1-KF01A配置了高精度的姿控系統，如表2所示，可有效降低成像過程中的隨機誤差。

表2 吉林一號寬幅01星高精度姿控系統信息Tab.2 Detailed information of high-precision attitude control system of Jilin1-KF01A

外方位元素定標的本質是建立設備安裝誤差和姿軌測量過程中系統誤差的補償模型。由公式（1）可以看出，GPS相關誤差所引起的幾何定位誤差為平移誤差，可等效為衛星轉動微小角度引起的誤差，相機安裝誤差與姿態測量系統誤差具有等效性［15］，因此可構建廣義安裝矩陣作為外方位元素定標模型。與此同時，顧及衛星成像是運動成像這一特性，應在模型中考慮運動過程中的姿態漂移，因此采用顧及時間特性的偏置矩陣模型作為外方位元素定標模型，即有：

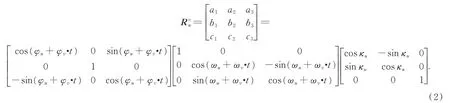
內方位元素定標模型的本質是恢復成像探元在衛星坐標系下的真實指向，因此可以采用探元指向角模型［16］來表達內方位元素。探元指向角模型如圖1所示，即像元(x y f)T在相機坐標系下的指向角可表示為(tanψxtanψy1)T，即：

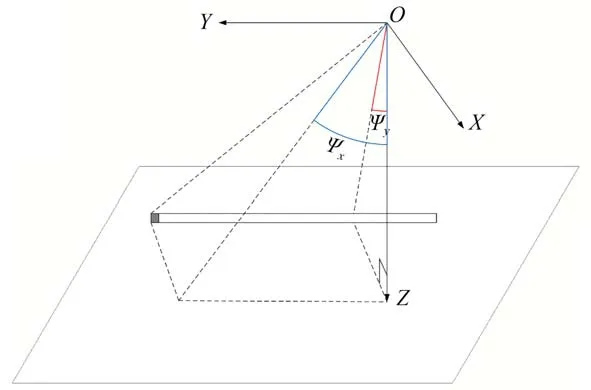
圖1 探元指向角示意圖Fig.1 Schemetic diagram of detector direction angle

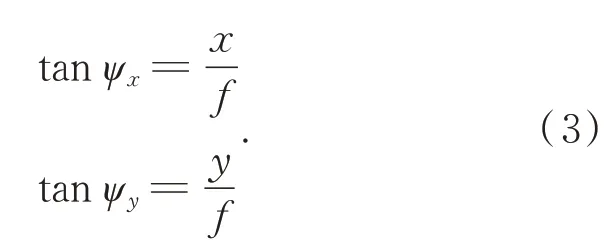
本文采用基于多項式的指向角模型，即利用多項式對相機內各CCD上的各探元在相機坐標系下的探元指向角(tanψxtanψy)進行擬合，基于探元指向角模型及附帶顧及時間特性的偏置矩陣模型的亞米級寬幅相機的嚴密幾何模型如下：

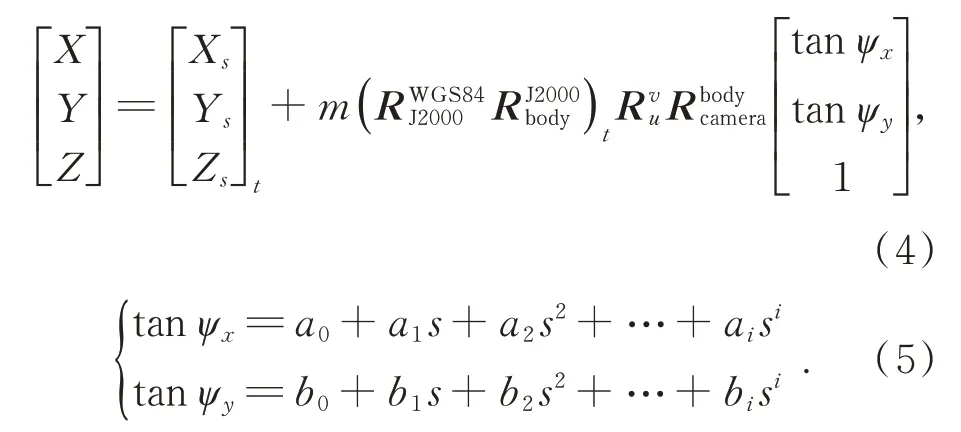
2.2 亞米級寬幅相機在軌幾何定標方法

Jilin1-KF01A的亞米級寬幅相機成像鏈路較為復雜，盡管可以通過內外方位元素定標分別補償相機內外部的系統誤差，但是內外方位元素間存在著強相關性，同時解算難以得到可靠的解算結果。因此，需采用內外方位元素分步迭代的策略進行在軌幾何定標參數解算，并且少量控制點難以取得高精度的幾何定標結果。本文采用高精度密集匹配算法，將Jilin1-KF01A獲取的待定標影像與定標場的數字正射影像（Digital Ortho‐photo Map，DOM）和數字高程模型（Digital Ele‐vation Model，DEM）等控制數據進行密集匹配，獲取分布均勻的密集控制點來增加定標模型中觀測方程的數目，提升在軌幾何定標參數的求解精度。

Jilin1-KF01A的亞米級寬幅相機采用超多片線陣TDI CCD機械交錯拼接，成像幅寬達到了136 km，全視場探測器拼接而成的單景數據量過大，不便于數據生產與處理，因此該相機傳感器校正產品在實際生產中按照23 km幅寬片分為6組，在軌幾何定標也按照6組進行。如表1所示，亞米級寬幅相機共包含5個譜段，其中紅、綠、藍、近紅外譜段具有相同的地面分辨率，因此針對每組內全色譜段影像以控制數據為基準進行在軌幾何定標，獲得其內外方位元素的定標參數；全色與多光譜數據具有相同的安裝誤差和姿軌測量誤差的補償模型，因此針對多光譜譜段僅需要進行內方位元素定標參數解算。考慮到具有相同分辨率的多光譜影像間由于探測器在焦平面上的排布位置不同，對相同地物成像具有不同的成像視角及成像姿態，分別與控制數據進行絕對定標難以獲得較高的譜段間配準精度，因此選取藍譜段為基準譜段與控制數據進行絕對定標，其余多光譜譜段與基準譜段進行高精度密集匹配獲取控制點進行內方位定標參數解算，實現基于基準譜段的譜段間相對定標。

Jilin1-KF01A亞米級寬幅相機采用離軸三反式光學設計，探測器采用線陣TDI-CCD機械式交錯拼接。CCD品字型偏視場設計使得相機對地成像時同一時間獲取的影像不共線，如圖2所示，相鄰CCD間獲取相同地物P的影像P1與P2存在約0.6 s的時間差，即P1與P2為衛星處于不同位置、時間、姿態及視角下拍攝獲取的P點的像。同時，相鄰CCD間搭接處在光學系統中具有不同的畸變系數，這極大地增加了相鄰CCD間影像的內視場無縫拼接難度。為解決相鄰CCD間相同區域影像拼接錯縫的問題，本文在原有定標模型的基礎上，引入附加片間幾何定位一致性約束條件進行在軌幾何定標，即相鄰CCD在不同條件下獲取的同一區域影像應具有一致的物方地理坐標。通過將片間幾何定位一致性約束條件加入到在軌幾何定標解算模型中，提升相鄰CCD間內方位元素定標系數的精度，從而實現相鄰CCD間影像的無縫拼接。基于該約束條件，需在定標過程中對相鄰CCD間獲取的同一區域影像進行密集匹配獲取CCD片間連接點，通過各自嚴密成像幾何模型解算連接點的地理坐標。該地理坐標為帶偏計算值，因此基于幾何一致性定位條件取作為物方地理坐標參與定標系數解算。

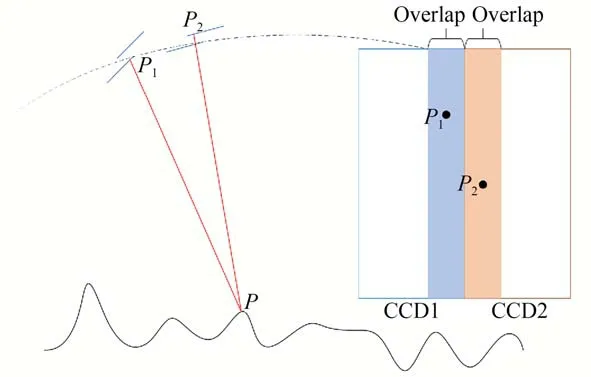
圖2 CCD搭接區域成像示意圖Fig.2 Schematic diagram of CCD overlapping area im‐aging

2.3 在軌幾何定標流程

Jilin1-KF01A的亞米級寬幅相機的在軌幾何定標流程如圖3所示。

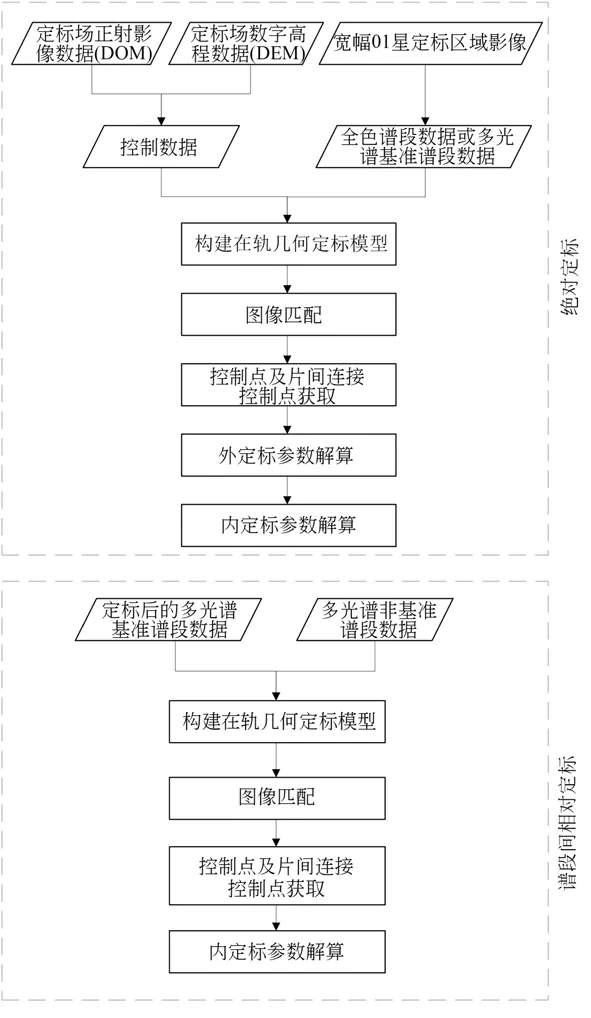
圖3 寬幅01星寬幅相機定標流程Fig.3 Flow chart of on-orbit geometric calibration of Ji‐lin1-KF01A WF camera

針對全色譜段和多光譜基準譜段，采用附帶片間幾何定位一致性約束的分步迭代法，在軌幾何絕對定標的具體步驟如下：

（1）利用實驗室幾何定標系數構建初始在軌幾何定標模型；

（2）在影像中選取定標區域，針對該區域通過圖像匹配算法對待定標影像與控制數據進行高精度密集匹配，獲得均勻分布的N個控制點（控制點的WGS84地心直角坐標為[Xi Yi Zi]T，對應的像點坐標為[(xLi yLi)，(xRi yRi)]T，i=1，2，3，…，N）；

（3）對定標區域內相鄰CCD拍攝的相同目標區域通過圖像匹配算法進行高精度密集匹配，獲得M個控制點（控制點的WGS84地心直角坐標為[Xi Yi Zi]T，對應的像點坐標為[xi yi]T，i=1，2，3，…，M）；

（4）將式（4）恒等變換為：

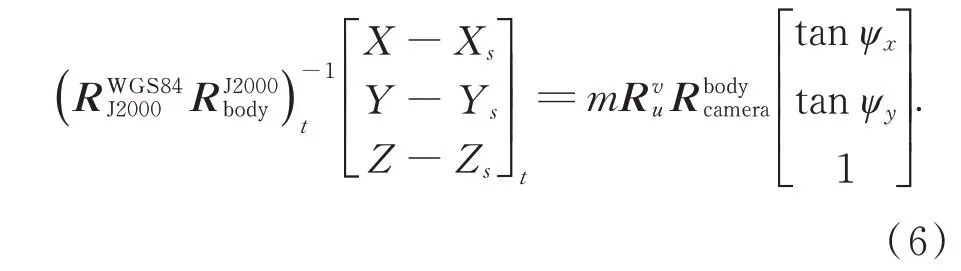
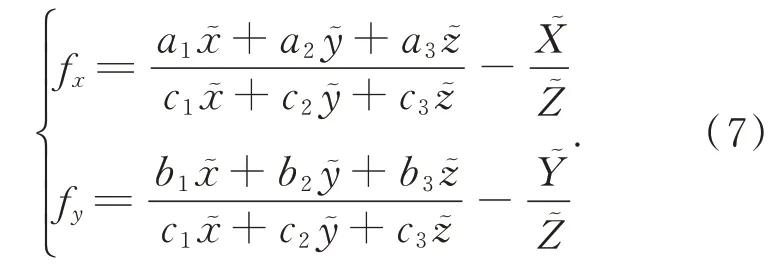
（5）將當前內定標系數視為“真值”，根據在軌幾何定標模型對式（7）進行線性化，建立誤差方程，求解外定標系數[φuωuκuφvωv]T，并更新幾何定標模型；

（6）將求得的外定標系數視為“真值”，利用在軌幾何定標模型對式（7）進行線性化，建立誤差方程，求解內定標系數并更新幾何定標模型；

（7）重復步驟（4）~（5），直至求解的內外方位元素定標系數趨于穩定，停止迭代計算；

（8）利用計算得到的內外方位元素定標系數更新相機的幾何定位模型參數。

針對多光譜非基準譜段，采用附帶片間幾何定位一致性約束的分步迭代法，在軌幾何相對定標的具體步驟如下：

（1）構建初始在軌幾何定標模型；

（2）在影像中選取定標區域，針對該區域通過圖像匹配算法對待定標影像與基準譜段數據進行高精度密集匹配，獲得均勻分布的N個控制點（控 制 點 的WGS84地 心直角坐標為[Xi Yi Zi]T，對應的像點坐標為[(xLi yLi)，(xRi yRi)]T，i=1，2，3，…，N）；

（3）對定標區域內相鄰CCD拍攝的相同目標區域通過圖像匹配算法進行高精度密集匹配，獲得M個控制點（控制點的WGS84地心直角坐標為[Xi Yi Zi]T，對應的像點坐標為[xi yi]T，i=1，2，3，…，M）；

（4）將基準譜段求得的外定標系數視為“真值”，利用在軌幾何定標模型求解內定標系數，并更新幾何定標模型；

（5）重復步驟（4），直至求解的內方位元素定標系數趨于穩定，停止迭代計算；

（6）利用計算得到的內方位元素定標系數與基準譜段的外方位元素定標系數更新相機中對應譜段的幾何定位模型參數。

3 試驗結果與分析

3.1 試驗數據

為了驗證本文定標模型及方法的正確性，對Jilin1-KF01A亞米級寬幅相機進行在軌幾何定標實驗，定標數據如圖4所示。

圖4 實驗數據示意圖Fig.4 Schematic diagram of experiment data

3.2 定標結果及分析

依據前文描述的TDI CCD分組規則，對6組內的各譜段數據按照本文提出的方法進行了在軌幾何定標。定標后的幾何定位殘差如表3所示，多光譜譜段的譜段間配準精度如表4所示。統計了全色譜段定標前后的指向角差異，得到4片CCD的畸變如圖5所示，定標前后相鄰CCD間的影像拼接如圖6所示。定標統計結果表明，原始相機參數中由于存在非線性的幾何畸變，相鄰CCD間的影像拼接存在嚴重錯位，無法滿足多片CCD影像高精度幾何拼接精度要求；經過在軌幾何外方位元素定標后，修正了幾何定標模型中的設備安裝誤差，通過附帶片間幾何定位一致性約束的在軌內方位元素定標，有效消除了相機內部的非線性畸變，各片CCD影像之間具有基本一致的幾何定位精度，實現了相鄰CCD片間的無縫拼接；與此同時，通過消除多光譜譜段間的幾何定位誤差，實現了譜段間的高精度匹配。

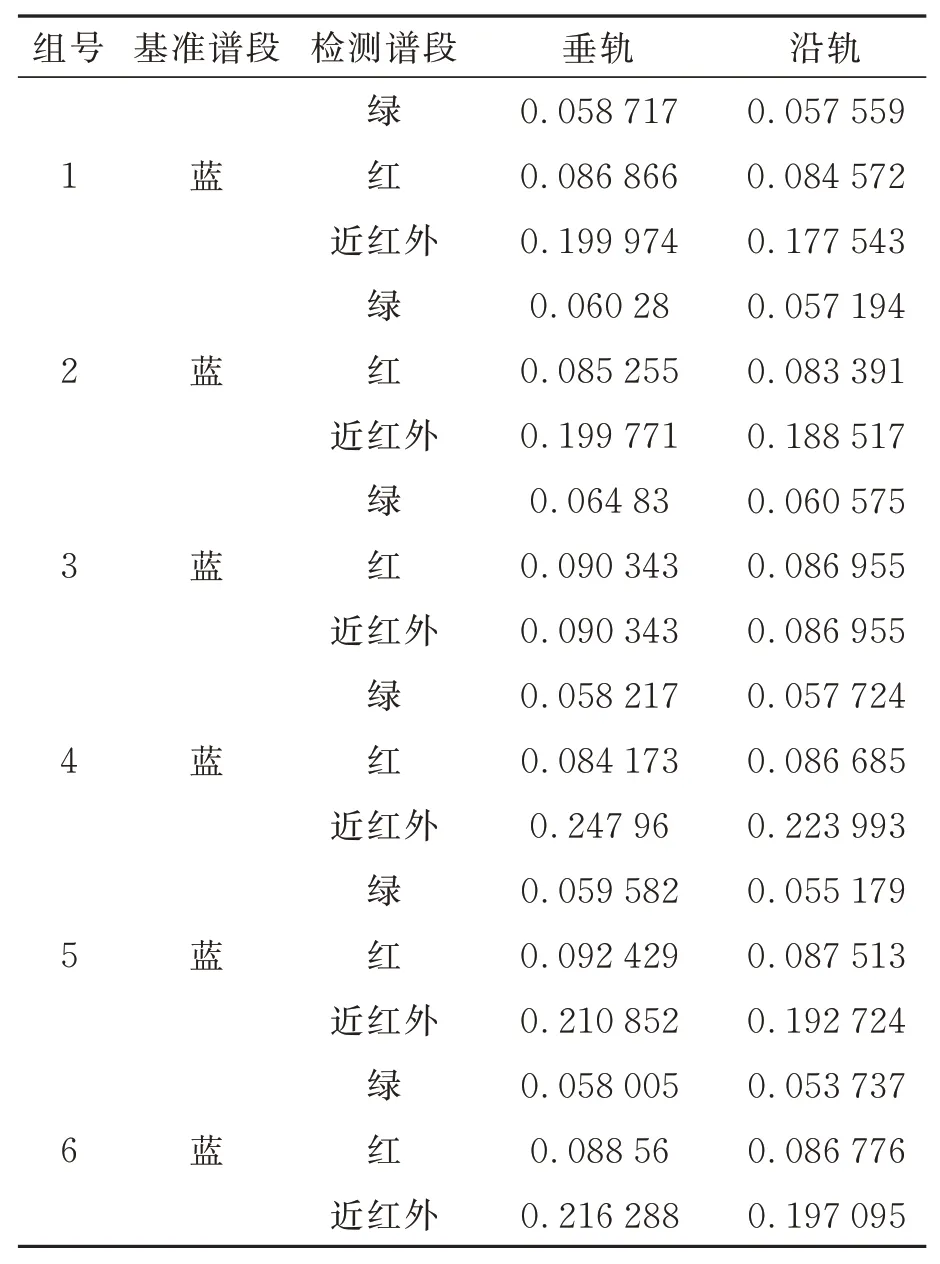
表4 定標數據譜段間配準精度Tab.4 Band-to-band registration accuracy of calibration images （pixel）

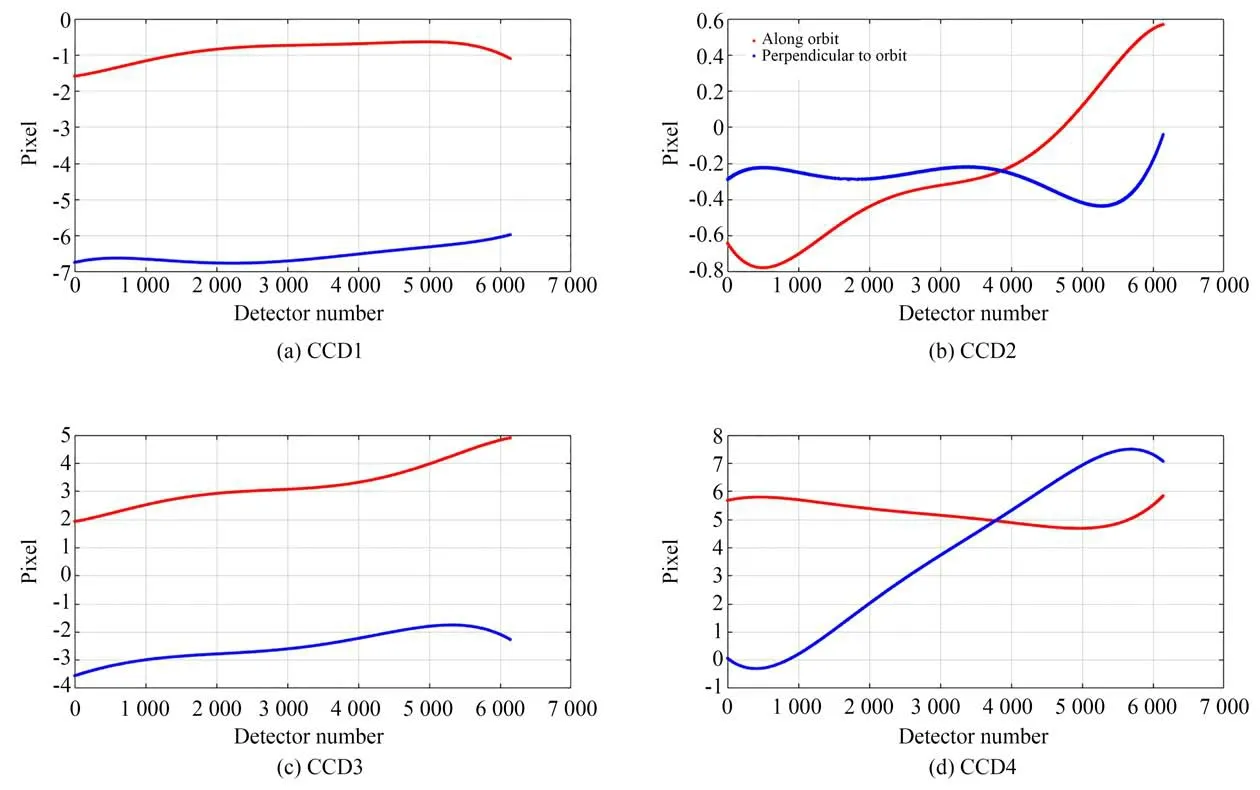
圖5 定標前后全色譜段CCD1~CCD4內部畸變曲線Fig.5 Internal distortion curves of panchromatic bands CCD1-CCD4 before and after calibration

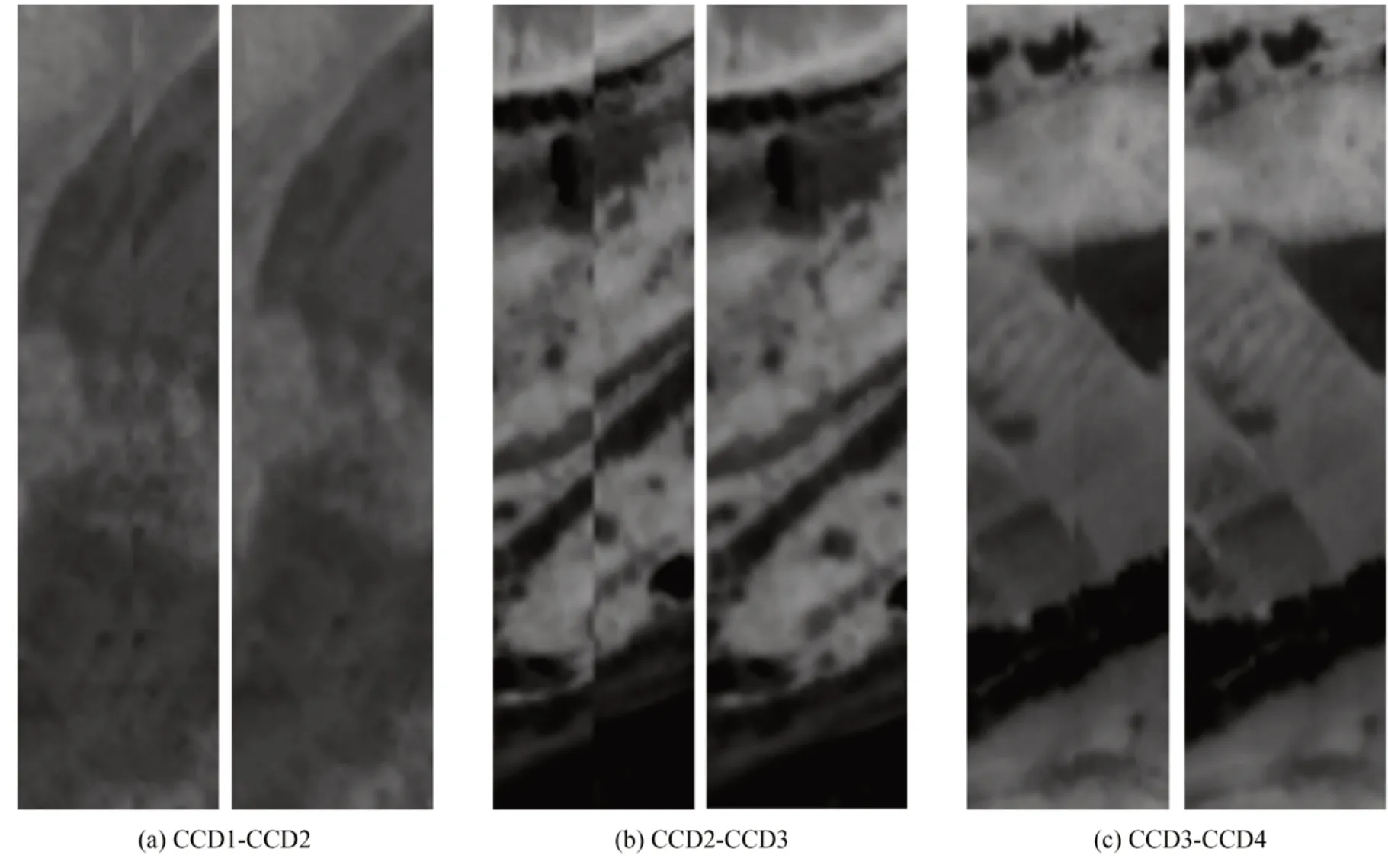
圖6 定標前后片間幾何拼接對比Fig.6 Comparison of geometric stitching before and after calibration

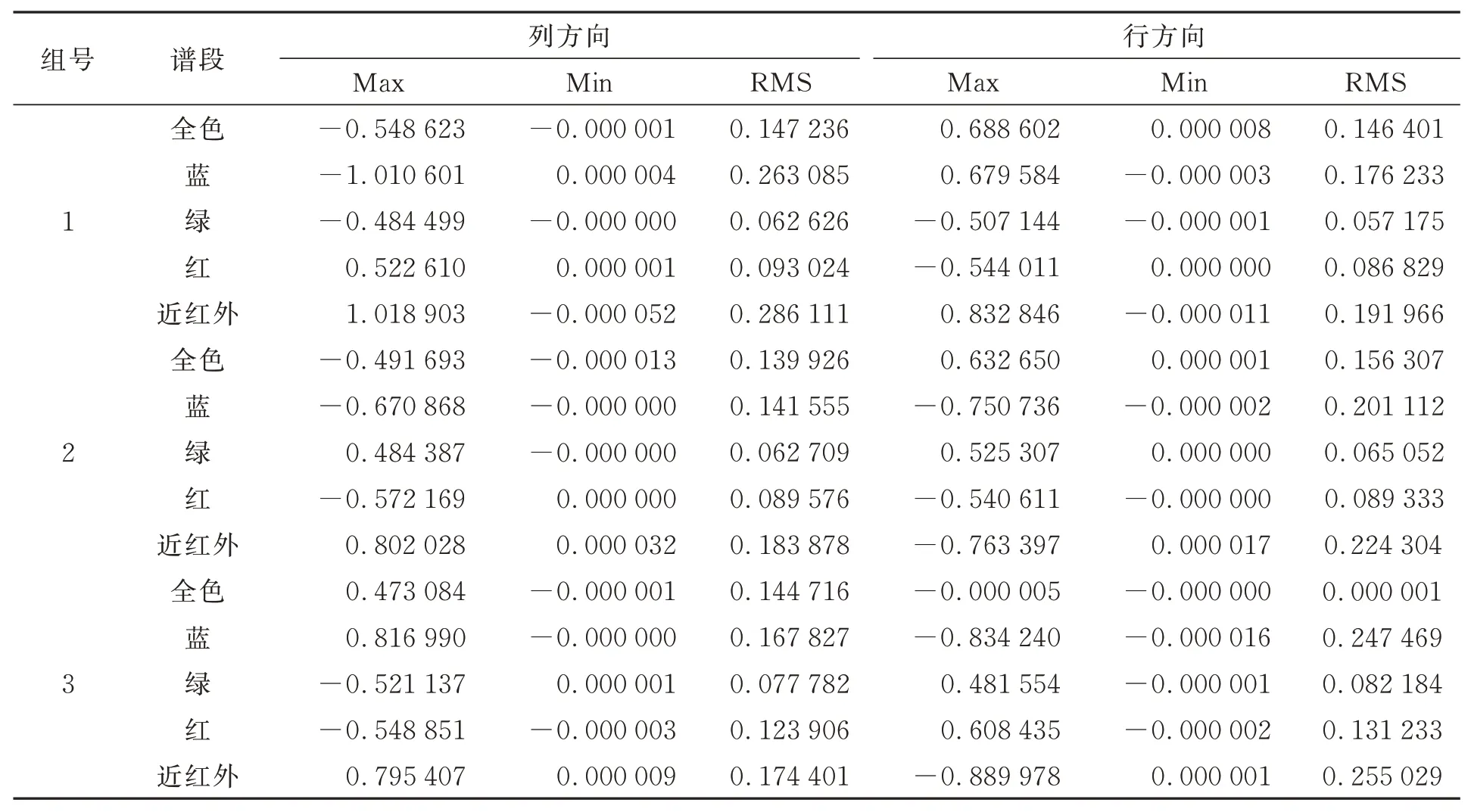
表3 在軌定標殘差統計Tab.3 Statistics of on-orbit calibration residuals （pixel）

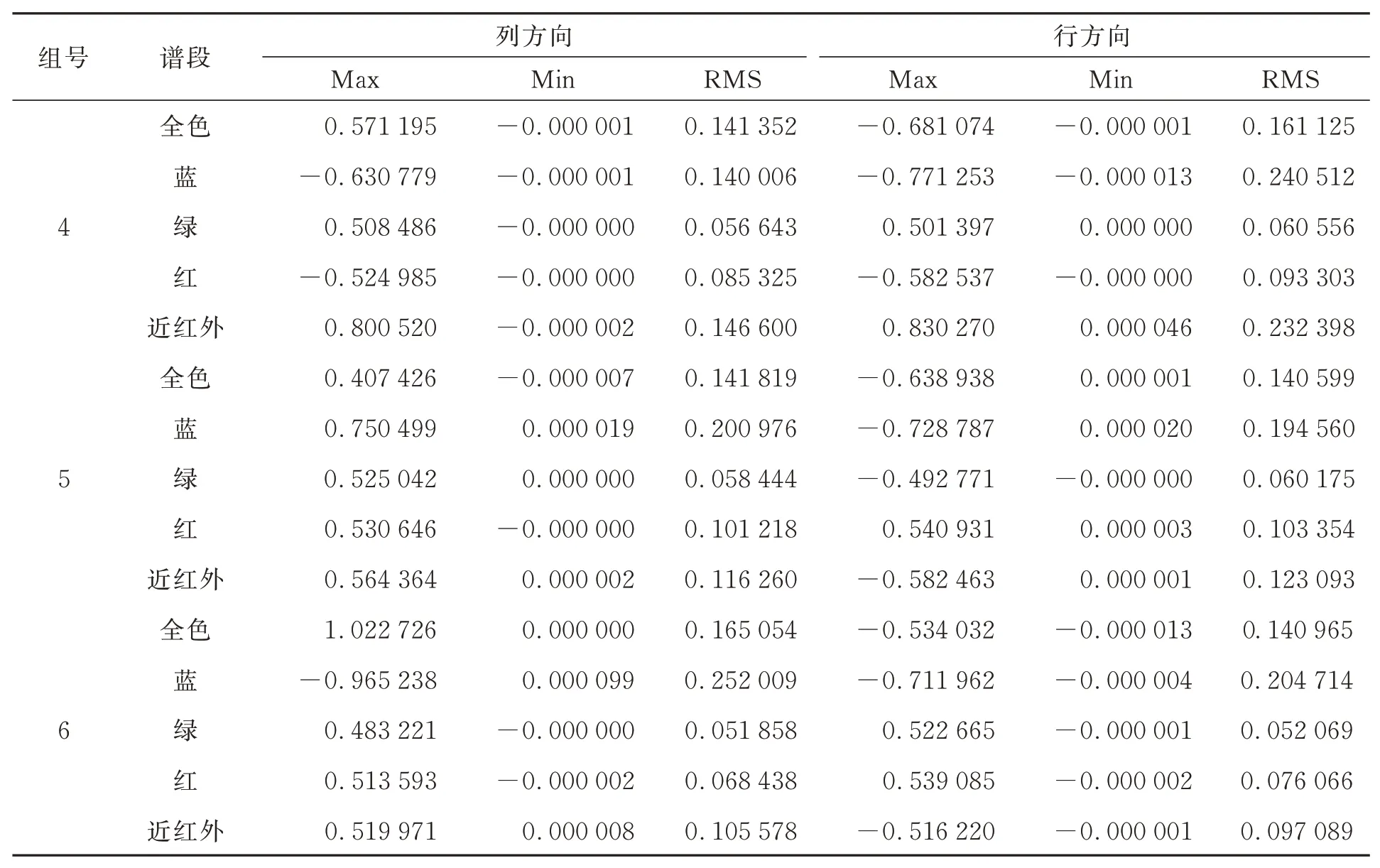
續表3 在軌定標殘差統計Tab.3 Statistics of on-orbit calibration residuals （pixel）

3.3 幾何精度驗證

為了保證定標參數結果的可靠性與適用性，需要對Jilin1-KF01A在軌運行期間的數據進行幾何精度驗證。將在軌幾何定標獲得的參數作為輸入進行寬幅相機L1級標準影像數據生產，本文隨機選取了10軌不同數據，用于Jilin1-KF01A亞米級寬幅相機影像的無控定位精度及譜段間配準精度測試，實驗數據分布在不同區域。利用實驗數據與參考影像自動密集匹配，獲得分布均勻的同名點，并統計每一景影像的同名點的定位結果作為無控定位精度。此外，針對實驗數據中多光譜影像的譜段間配準精度，以藍譜段為基準譜段，分別與綠譜段、紅譜段、近紅外譜段進行自動密集匹配，獲得分布均勻的同名點，統計同名點在垂軌與沿軌方向的偏差，統計結果如表5所示。

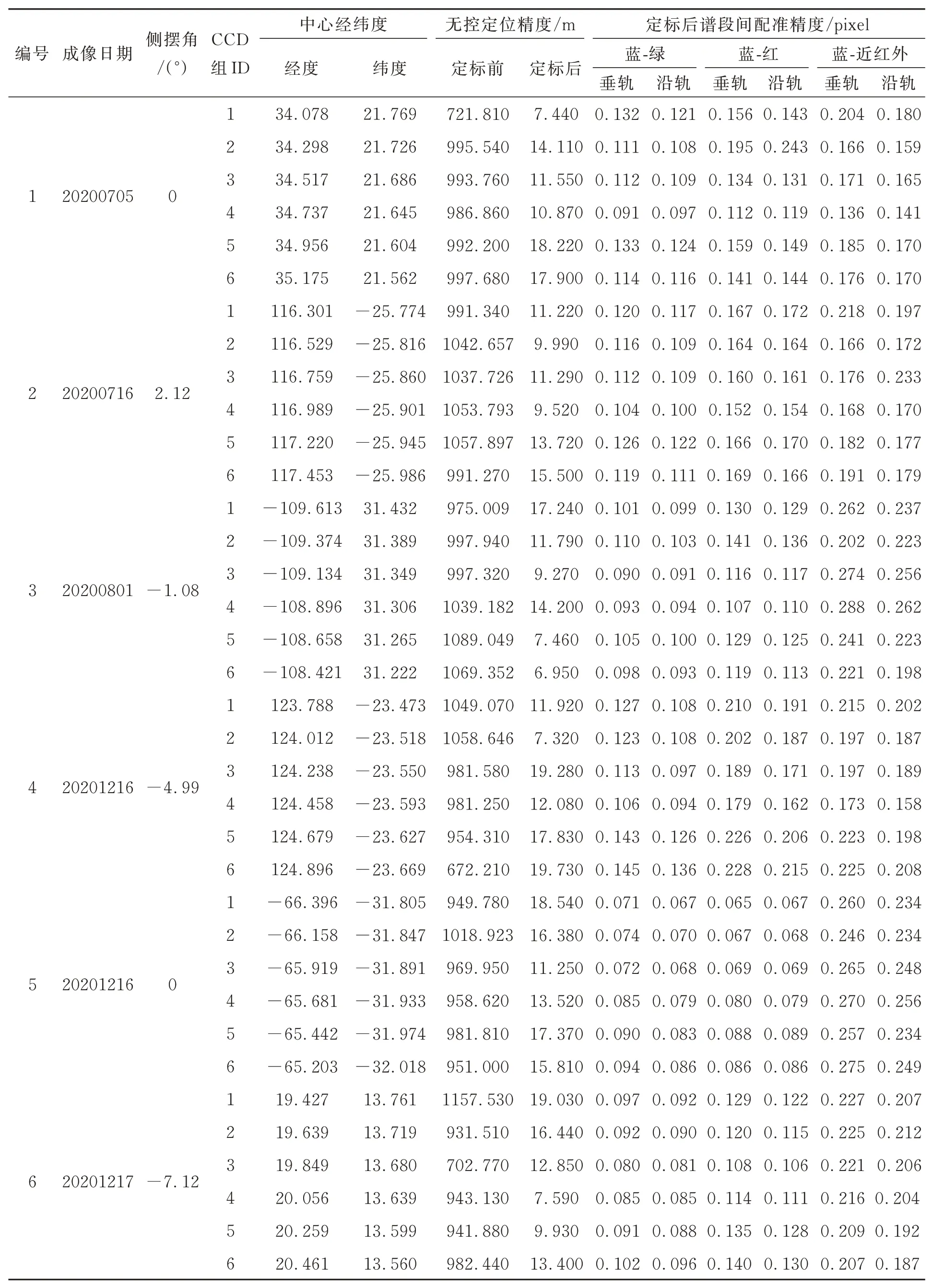
表5 無控定位精度及譜段間配準精度Tab.5 Positioning accuracy without GCPs and band-to-band registration accuracy

在軌幾何定標參數中不可避免地引入了一些定標景數據的隨機誤差，衛星不同軌成像獲取的數據中包含不同的隨機誤差，因此定標系數中補償的定標數據隨機誤差和衛星在其他時間獲取數據中的隨機誤差均會影響數據的幾何定位精度。在軌幾何定標消除了成像模型中的系統

誤差，極大地提升了數據整體的無控定位精度，使用在軌幾何定標參數后的數據無控定位精度優于20 m（CE90），同時提升了譜段間的定位一致性，譜段間配準精度優于0.3 pixel，消除了相鄰CCD間影像的拼接縫，實現了亞米級寬幅相機高精度幾何校正數據產品的生產。

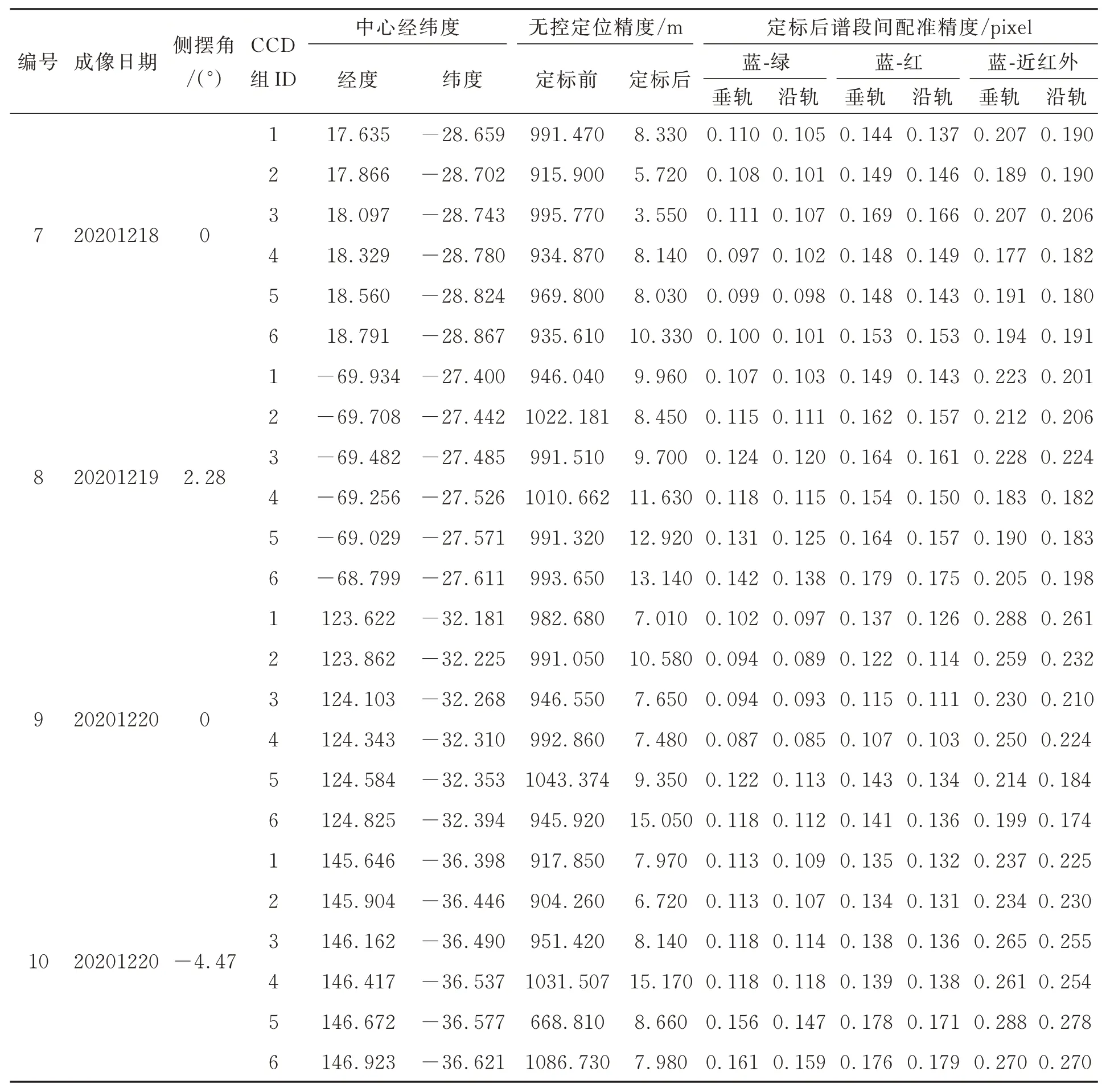
續表5 無控定位精度及譜段間配準精度Tab.5 Positioning accuracy without GCPs and band-to-band registration accuracy

將遙感影像數據用于高精度制圖時，需要通過控制點進一步消除數據中的幾何定位誤差，因此，帶控定位精度決定了遙感影像數據能否用于高精度制圖。本文通過在吉林省長春市范家屯區域的43個高精度控制點（控制點精度優于0.1 m），對該區域的5景Jilin1-KF01A寬幅相機L1級標準影像數據利用5個控制點進行帶控幾何校正，并利用10個以上檢查點對帶控幾何校正后的數據進行精度分析。控制點分布如圖7所示，統計檢查點的幾何定位誤差，帶控幾何精度統計結果如表6所示。實驗結果表明，Ji‐lin1-KF01A寬幅相機利用在軌幾何定標系數生產的L1級標準影像產品的帶控精度優于2 m，滿足1∶10 000的制圖需求。

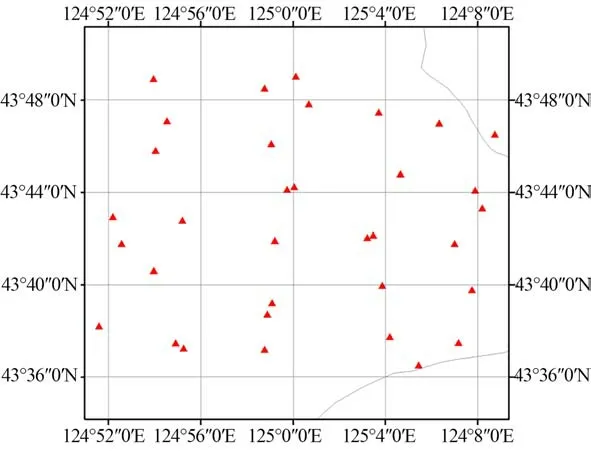
圖7 控制點分布圖Fig.7 Distribution map of control points

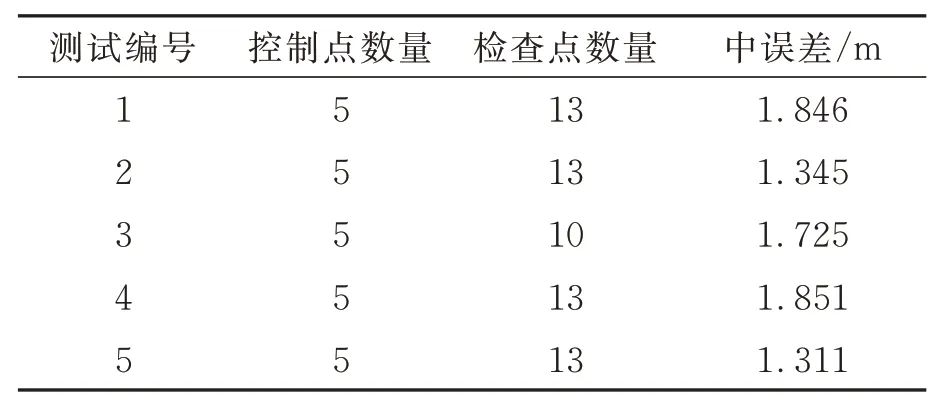
表6 帶控定位精度統計表Tab.6 The statistics of positioning accuracy with GCPs

4 結 論

本文基于Jilin1-KF01A亞米級寬幅相機大口徑、大視場、長焦距、離軸三反式光學系統以及探測器采用超多片TDI CCD機械交錯拼接的特點，提出了基于探元指向角模型附帶片間幾何定位一致性約束的在軌幾何定標方法。該方法采用外定標元素與內定標元素分步循環求解的策略，針對全色及多光譜基準譜段利用DOM與DEM進行了絕對定標試驗，對多光譜非基準譜段利用已經定標后的多光譜基準譜段進行了相對定標試驗，并對定標后影像的幾何精度進行了分析和驗證。實驗結果表明，本文使用的定標方法及定標模型合理有效，能顯著提升Jilin1-KF01A亞米級寬幅相機的無控定位精度，定標后無控定位精度優于20 m（CE90），定標內定標精度優于0.3像元，多光譜譜段間配準精度優于0.3像元，實現了超多片TDI CCD機械式拼接的無縫拼接影像生成，稀疏帶控精度優于2 m，可滿足1∶10 000的制圖需求。