基于Copula方法的城市排水排澇設計標準協調性研究

鐘逸軒，廖小龍，易 靈，吳樂平

（中水珠江規劃勘測設計有限公司，廣州510000）

1 研究概述

據《2019 中國統計年鑒》［1］，2018年末中國城鎮人口達8.31億人，城鎮化率從改革開放之初1978年的17.92%增加至2018年的59.58%，城市內澇災害事件的潛在危害性也隨之急劇上升［2］。國務院2013年發布關于提升城市基礎設施能力的若干意見，其中就特別指出要在十年內顯著改善市政排水系統和城市排澇系統的能力。2015年和2016年，共計30 座城市分批被選作海綿城市建設試點，用以推行海綿城市相關技術，探索整治城市內澇災害的經驗。總的來說，城市排水排澇對于城市管理和災害預防的重要作用得到了人們普遍認可，也引發了學者們的廣泛研究［3-6］。

城市排水排澇設計標準是海綿城市建設的重要依據，直接決定了城市的內澇防御標準以及市政排水和城市排澇系統規模。然而，長期以來我國排水系統和排澇系統分屬不同部門管理，也遵循不同設計規范，尚未形成統一的標準銜接方法，存在設計標準不相協調的情況［7，8］。設計標準協調性研究通過科學闡述城鎮排水排澇之間的相互作用與影響規律，基于城鎮排水排澇系統的水力聯系和特性差異，采用一定方法確定不同系統各自的設計規模，實現設計標準的銜接。張明珠等［9］基于芝加哥雨型和相關分析法推算了市政排水和水利排澇的設計重現期銜接關系，結果表明同量級的暴雨事件，水利排澇計算重現期標準約為市政排水計算重現期的5 倍。李衛東和徐向陽［5］研究認為，市政排水受阻的重要原因之一是水利排澇系統無法及時排除澇水，導致內河道水位過高對排水管道形成頂托，并給出了不同設計標準下排水排澇系統的設計重現期銜接關系。陳鑫等［10］提出通過SWMM 模型對研究區域開展城市雨洪模擬，將設計長短歷時組合暴雨過程作為輸入，研究給定重現期組合條件下能否滿足城鎮內澇防治需求。楊星等［11］基于貝葉斯公式推算了不同排水排澇設計重現期的組合風險率，并提出組合風險率應當近似于水利排澇設計標準，以節約投資的同時保障滿足設計需求。陳子燊等［12］分析了城市兩級排澇標準銜接方法，通過Copula 方法計算了不同歷時暴雨聯合分布，并基于二次重現期定義了城鎮兩級排澇標準的設計重現期，分析不同重現期設計標準組合情況下系統整體的內澇防御標準。

本文在現有研究的基礎上，以中山和珠海市為例開展城市排水排澇設計標準協調性研究，具體為基于Copula 理論獲取排水排澇設計標準的聯合重現期，評價給定城市排水排澇系統設計組合下的整體內澇防御標準，并給出指定Kendall重現期條件下的最可能排水系統和排澇系統的設計標準組合。相比現狀水利和市政部門分別確定排水排澇系統建設規模，本研究給出的方法可有效避免上述系統設計標準不協調帶來的內澇風險，實現了不同系統設計標準間的有效銜接，可為開展海綿城市建設工作和城市內澇防御相關規劃設計提供科學可行的參考依據。

2 主要研究方法

2.1 Copula理論簡介

據Sklar 定理［13］，通過變量的邊緣分布和Copula 聯結函數可構建多元概率分布函數：

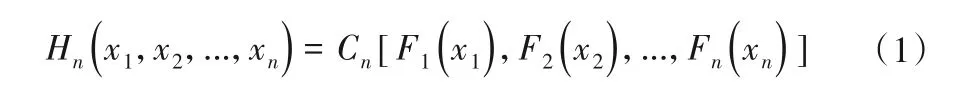
式中：Hn(x1，x2，...，xn)=P(X1≤x1，X2≤x2，...，Xn≤xn)表示X的n維概率分布函數；Fi（xi）表示Xi的邊緣累積分布函數（i=1，2，…，n）；Cn（·）表示Copula 函數，其選取與Fi（xi）無關，但需要能夠較好地描述邊緣分布的相關性結構。

近年來，Copula 理論因其不依賴與邊緣分布類型且聯結函數多種多樣的特點，被廣泛應用于水文氣象多變量聯合設計問題上［14-16］。二維Copula可用于建立不同時段長降雨量（如P1h和P12h）之間的聯合概率分布，即：

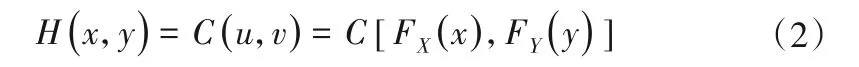
式中：X為短歷時降水；Y為長歷時降水；u=FX（x）和v=FY（y）分別為x和y的邊緣分布。

本研究采用皮爾遜三型分布（P3）、廣義極值分布（GEV）和對數正態分布（LN）作為降水序列的備選邊緣分布（見表1）。選用水文領域廣泛使用的三種阿基米德Copula 函數作為備選Copula分布［17，18］，具體見表2。邊緣分布和聯合分布采用均方根誤差（RMSE）、K-S檢驗和AIC準則進行優選［19-21］。

表1 3種用于降水量邊緣分布擬合的備選分布Tab.1 Three candidate distributions for precipitation series fitting

表2 3種不同的阿基米德Copula函數及其參數估計方法Tab.2 Three Archimedean Copula functions and parameter estimation method

2.2 聯合重現期

考慮到多變量設計問題中常用的“或”和“且”重現期存在明顯缺陷，對風險域的描述不夠客觀，存在相同聯合重現期的不同設計組合對應的風險域不同的問題［22］，本研究采用Kendall重現期用于描述城市排水排澇系統的整體內澇防御能力：

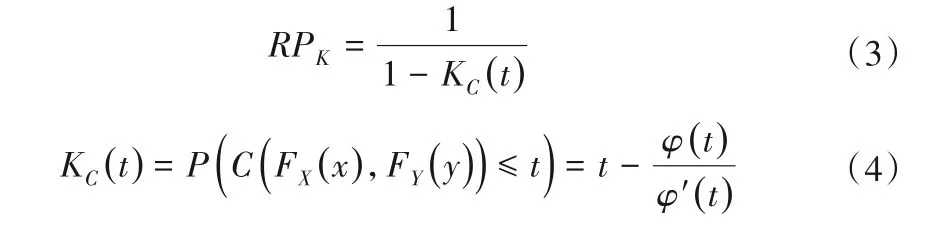
式中：t為Copula 聯合概率分布值；φ(·)為Copula 生成元，具體隨選用的Copula聯結函數而改變（見表2）。

2.3 設計標準銜接方法

最可能估計法（MLE）可避免多變量設計組合選取的任意性，因而被廣泛應用于洪水、暴雨、潮汐等多變量設計問題上［23-25］，其目標函數為：

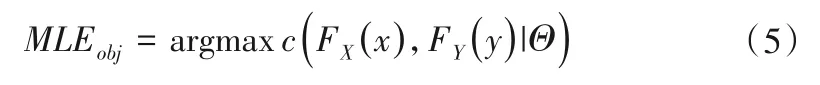
式中：c（·）為X與Y的聯合概率密度；Θ為給定條件。

基于Copula函數和MLE 原理，本文構建的城市排水排澇系統設計標準的銜接方法如下：①綜合確定城市內澇整體防御能力，以聯合重現期RP表示為n年一遇。②通過求解下式，獲取滿足步驟1 中給定RP的所有可能的排水和排澇系統設計組合(x*，y*)：

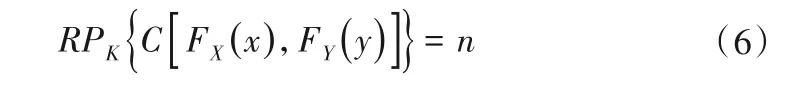
式中：RPK（·）為Kendall重現期。

③計算(x*，y*)的聯合概率密度，選擇概率密度最大的排水排澇系統的設計組合作為建議采用的設計組合：

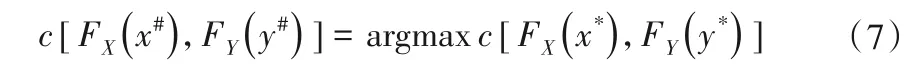
3 研究區域與數據

3.1 研究區域簡介

中山和珠海市位于珠三角區域（圖1）。長期以來，受水文氣象、地形地勢、人類活動等因素綜合影響，中山和珠海市頻繁遭受內澇災害的侵襲，對經濟社會可持續發展以及人民生命財產安全造成了嚴重不良影響。近年來，兩市有關部門在意識到城市排水排澇現狀短板的基礎上，結合自身經濟實力、可實施性等因素，編制了《海綿城市專項規劃》。考慮到城市排水系統和排澇系統設計標準銜接問題對科學制定工程規模至關重要，本研究以中山和珠海市為研究對象，基于Copula 理論開展排水系統和排澇系統的設計標準銜接研究，計算滿足城市內澇防治需求下的最優排水排澇設計標準組合，為城市內澇工程建設提供設計規模選取參考依據。

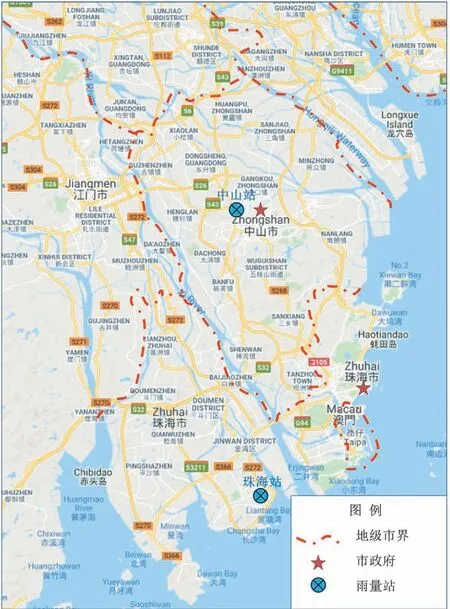
圖1 中山市和珠海市地理位置示意圖Fig.1 Map of Zhongshan city and Zhuhai city

3.2 數據與取樣方法

采用中山和珠海氣象站1962-2010年（共計49年）的小時降水數據。根據我國現行排水排澇系統設計規范，當資料序列長度超過20年時，推薦采用年最大取樣法進行分析計算。本研究中，首先從數據樣本中選取年最大1 h 降水量，然后再分別求算包含該1 h 雨量的年最大6、12 和24 h 累計降水量。其中1 h樣本用于排水系統設計，6、12 和24 h 樣本用于排澇系統設計。取樣結果見圖2。

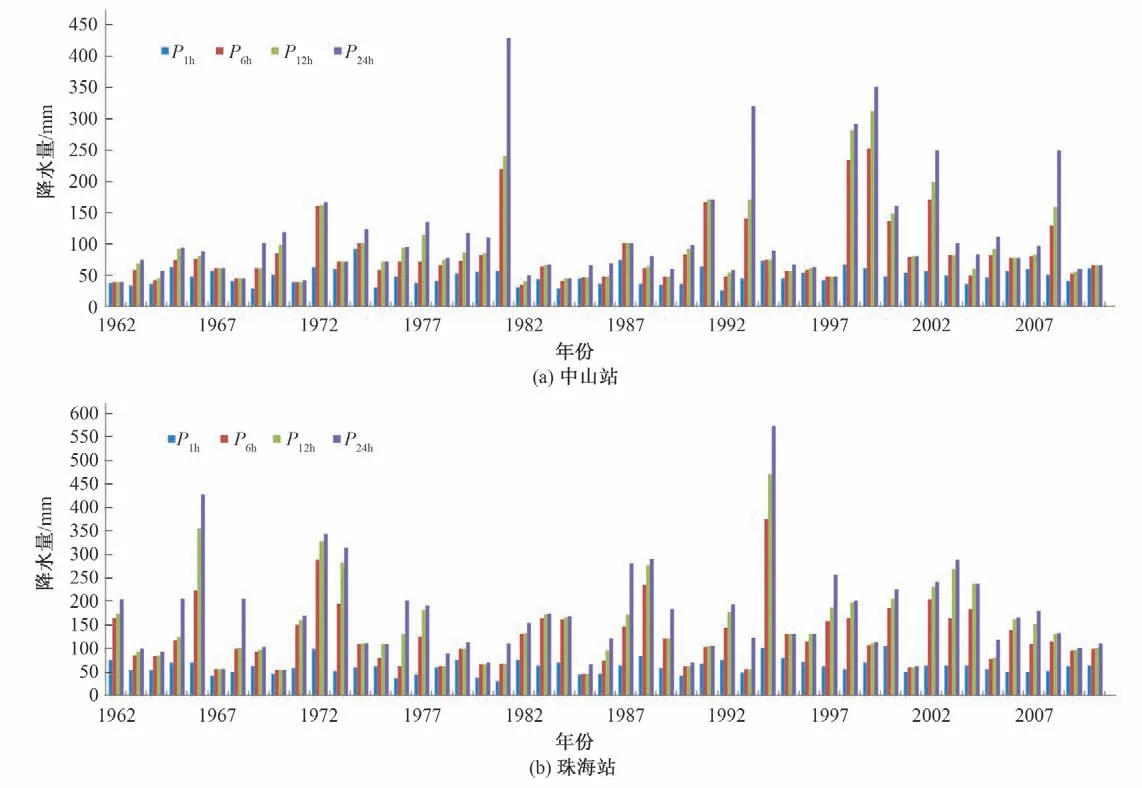
圖2 中山站和珠海站年最大法取樣結果Fig.2 Annual maximum sampling precipitation data of Zhongshan and Zhuhai

4 結果分析

4.1 邊緣分布擬合效果

表3 給出了不同擬合效果評價指標的結果，圖3 給出了不同邊緣分布下的Q-Q 圖。由表3 結果可知，在10%的顯著性水平情況下，由于不同時段長的降水量樣本的Dn值均小于給定的閾值，故3 種備選分布均通過了K-S 檢驗。進一步結合RMSE和AIC 進行分析，對于中山市的降水樣本，GEV 分布均具有最小的RMSE和AIC 值，而對于珠海市的降水樣本，LN 分布均具有最小的RMSE和AIC 值，因此，分別選用GEV 分布和LN 分布作為中山市和珠海市降水量的邊緣分布。值得注意的是，現行規范推薦的P3 分布對于兩個雨量站的各時段長樣本均不具有最佳的擬合效果。

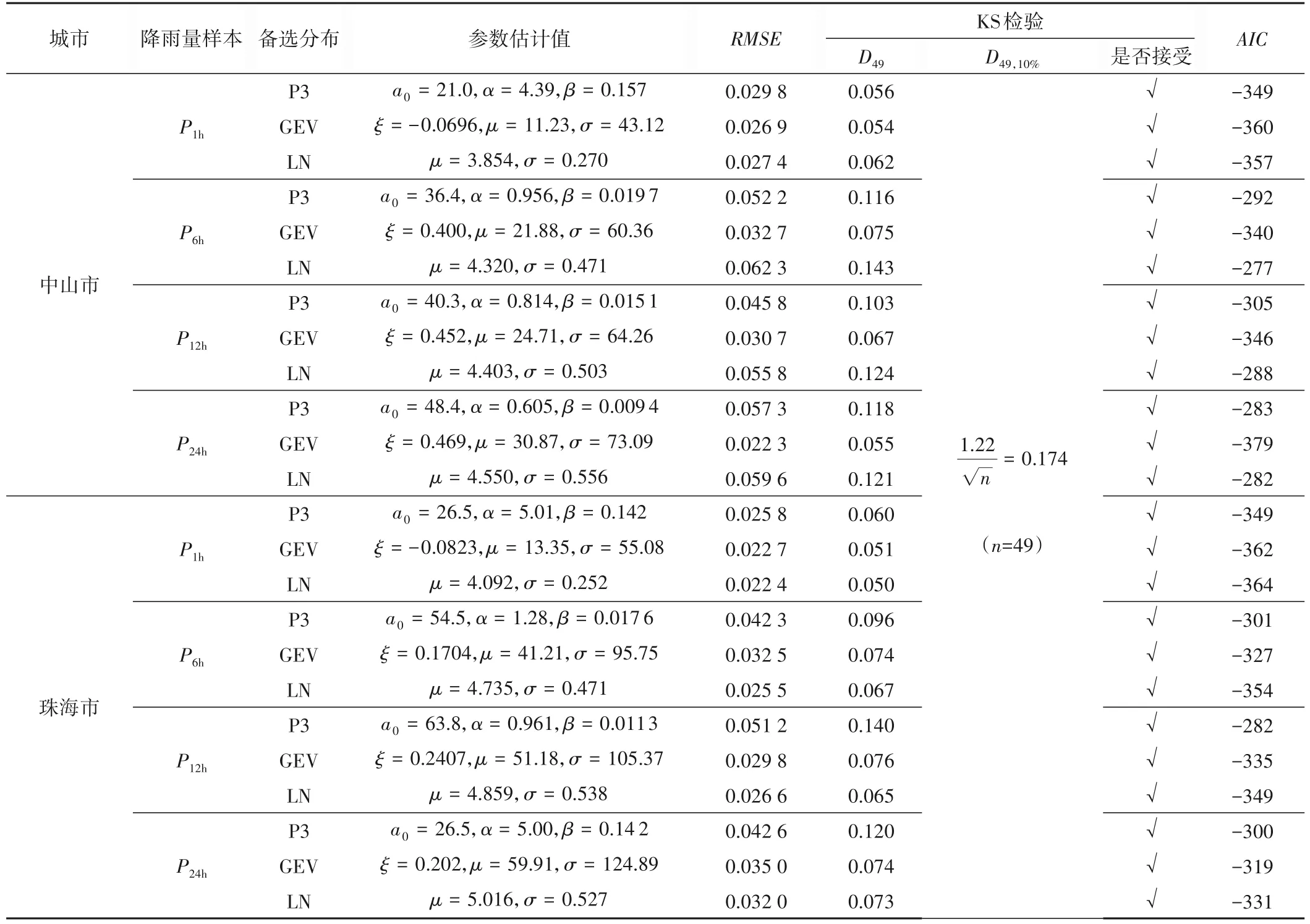
表3 不同邊緣分布的擬合優度評價效果Tab.3 Distribution fitting goodness evaluation results for different distributions

圖3 不同邊緣分布理論分布與經驗分布的Q-Q圖Fig.3 Q-Q plots of empirical distribution and different theoretical distributions

4.2 Copula聯合分布構建

邊緣分布確定后，根據Sklar 定理可以建立1 h 降雨量和其余不同時段長的降雨量樣本之間的Copula 聯合分布。本研究采用Kendall 秩相關系數法計算各時段組合的Copula 分布參數。不同Copula 函數的擬合優度檢驗結果見表4。K-S 檢驗統計量Dn表明，在10%置信水平下，3種阿基米德Copula均通過了檢驗。進一步分析RMSE和AIC結果，3種阿基米德Copula對于不同城市的不同時段長組合分別具有最小RMSE和AIC 值，不同于邊緣分布擬合優度檢驗結果，上述指標無法獲得一致結論。因此，僅依靠K-S 檢驗、RMSE和AIC 檢驗，無法有效識別最適合的Copula函數。Nguyen and Jayakumar的研究表明［26］，對于多變量極值設計問題，Frank 和Clayton 等不具備尾部相關性的Copula 函數通常并不適用，應當采用Gumbel 和Galambos 等可具有尾部相關結構的Copula 函數作為聯結函數。考慮本研究中3種備選Copula 函數僅有Gumbel分布具有上尾部相關性，本研究最終選取Gumbel Copula 函數用于中山和珠海市的不同降水量序列聯合分布構建。

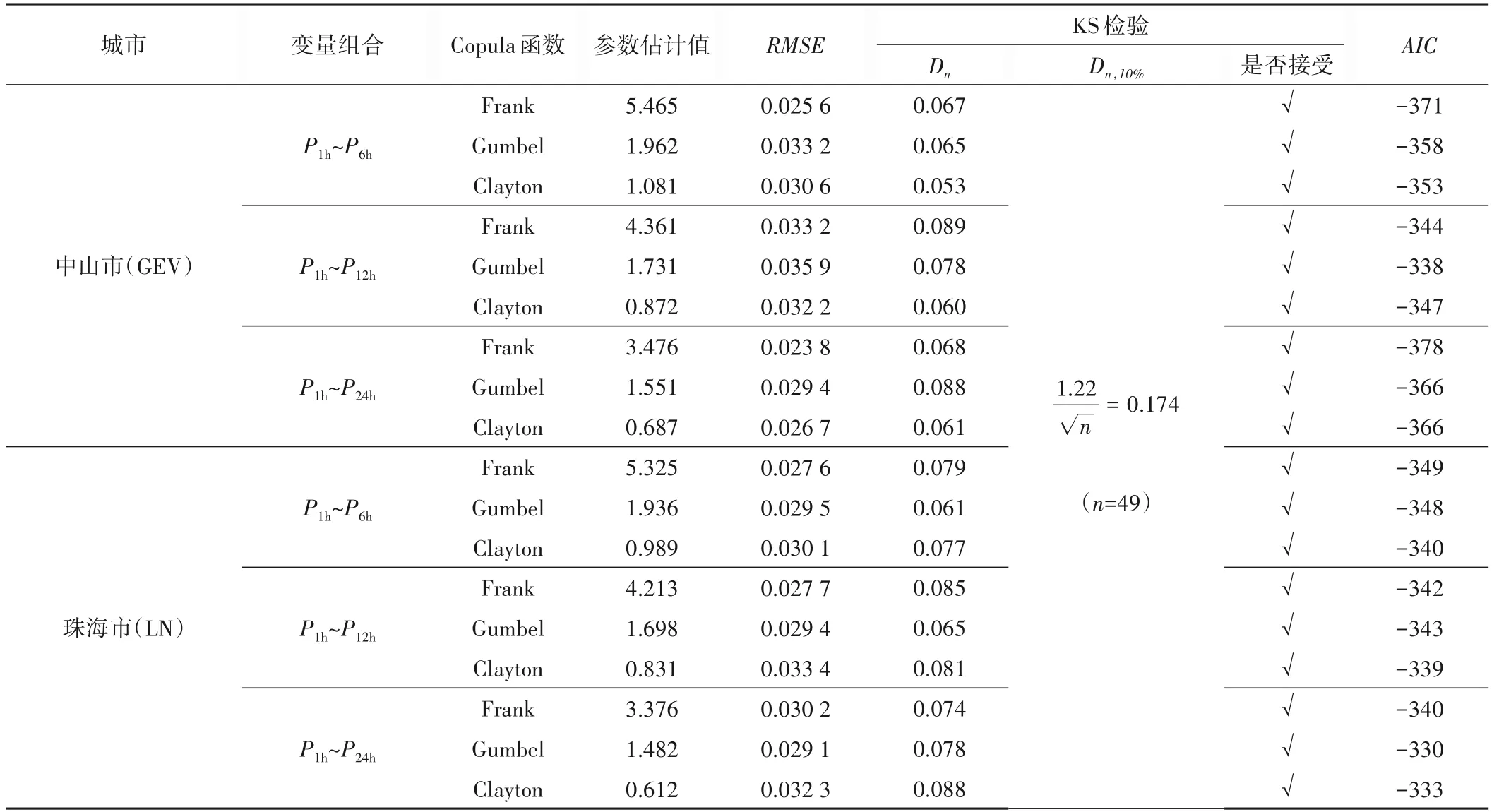
表4 不同Copula聯合分布的擬合優度評價效果Tab.4 Distribution fitness goodness evaluation results for different Copula functions

圖4Q-Q 圖中，經驗分布和Gumbel Copula 理論分布的點據基本位于1∶1線附近，表明Copula分布具有良好的擬合效果，故本研究建立的Copula 分布能夠準確描述中山市和珠海市不同時段長降雨量序列的相關結構，可據此構建排水排澇設計標準銜接，獲取具有協調性的設計降水量組合。

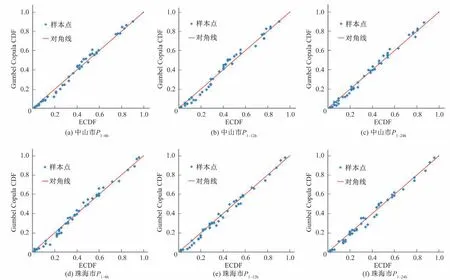
圖4 經驗頻率和Gumbel Copula理論概率分布值的Q-Q圖Fig.4 Q-Q plots of empirical distribution and Gumbel Copula distribution

4.3 不同排水排澇設計組合的聯合重現期

中山和珠海市各自的《海綿城市排水專項規劃》均提出了城區排水排澇系統規劃標準（表6），依據前述建立的Copula 聯合分布計算了不同情況下對應設計標準的Kendall重現期，結果表明中山市主要城區對應的Kendall 重現期為18～23 a，其他城區為5～6 a；珠海市主要城區對應的Kendall 重現期為26～37 a，其他城區為9～12 a。由表6 結果可知，當采用不同時段長降水量用于設計排澇系統規模時，各設計組合的Kendall重現期略有變化，并隨著時段長增加呈現上升趨勢，分析其原因在于較長時段的降雨量序列與年最大1 h 降雨量之間的相關性逐漸減弱，設計組合的不確定性更大，導致聯合概率分布值相對減小而Kendall 重現期增大。從實踐角度出發，Kendall 重現期相比單獨給出的排水系統和排澇系統重現期能夠更加直觀地描述城市整體內澇防御能力，便于決策者準確制定城市排水排澇系統規劃方案。

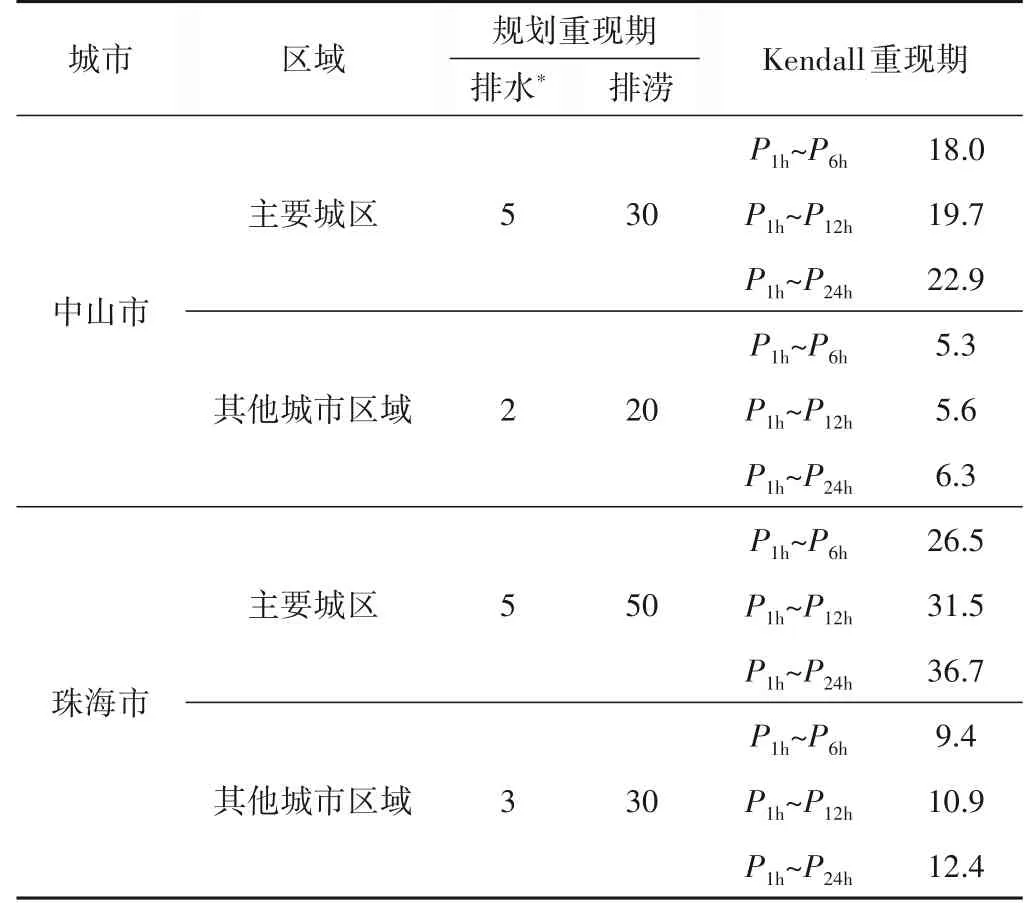
表6 中山和珠海市2020年規劃排水排澇系統設計重現期及Kendall重現期 aTab.6 Planning design standards of urban drainage and sewage systems in 2020 and the corresponding Kendall return periods for Zhongshan and Zhuhai

4.4 給定Kendall重現期的最可能設計組合

表7 給出了指定Kendall 重現期下的城市排水排澇設計標準最可能組合，由表7 可知，當中山市以Kendall 重現期表征城市內澇防御能力為20年一遇時，1 h 設計降雨量分別為69.9，69.4 和67.5 mm，相應的6、12 和24 h 設計降雨量分別為164.7，182.9和227.9 mm。

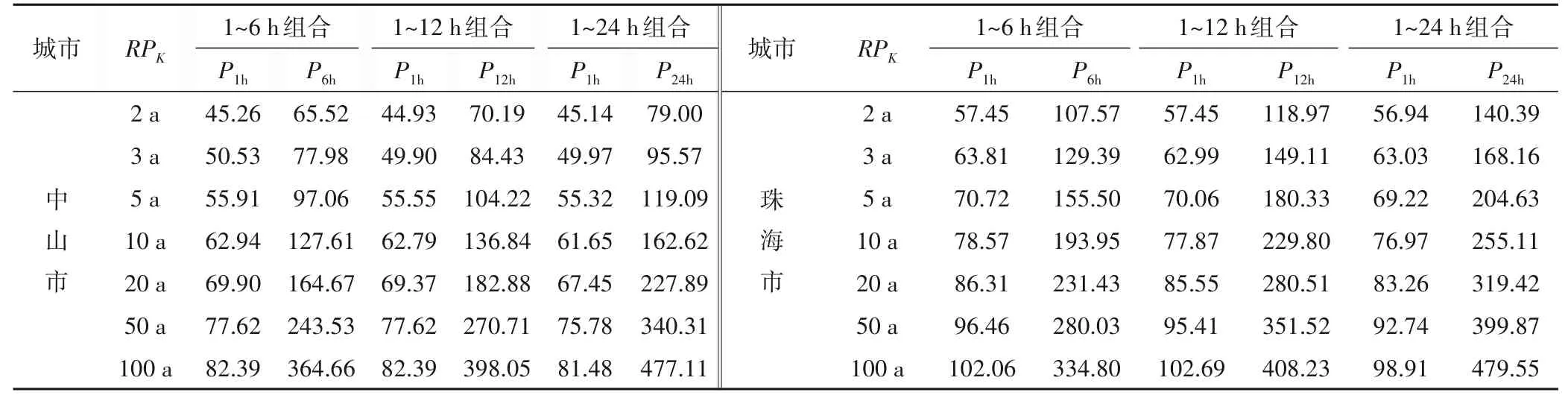
表7 給定Kendall重現期條件下的排水排澇設計降雨量組合 mmTab.7 Design precipitation combinations of urban drainage and sewage systems with given Kendall return periods

表8給出了上述設計值組合對應的邊緣重現期成果。以中山市為例，當以Kendall重現期表征的城市總體排水排澇防御能力為20年一遇時，若排澇系統采用12 h 降水設計，則最可能設計組合對應的排水系統以年多次法計算重現期約為6.6年一遇，以年最大法計算重現期約為13年一遇，相應排澇系統設計重現期為13年一遇。相比表6中中山市主城區排水設計標準5年一遇，排澇設計標準30年一遇，經協調后的設計排水標準有所提升，而排澇標準則相應降低，表明原規劃設計的排水系統規模偏小而排澇系統規模過大。計算結果同時表明，若中山市主城區以排水系統5年一遇作為整體設計依據，則其規劃排澇系統規模取值為15年一遇更為協調，即原規劃設計的排澇系統規模偏大，有可能造成投資浪費；若以排澇系統20年一遇作為整體設計依據，則排水系統協調后的規模應當為6年一遇，即原規劃設計的排水系統規模偏小，可能無法達到城市規劃的整體內澇防御水平。依據本研究提出的協調性方法，可在給出協調后的排水排澇設計標準組合的同時，幫助決策者對原規劃方案進一步作科學調整。

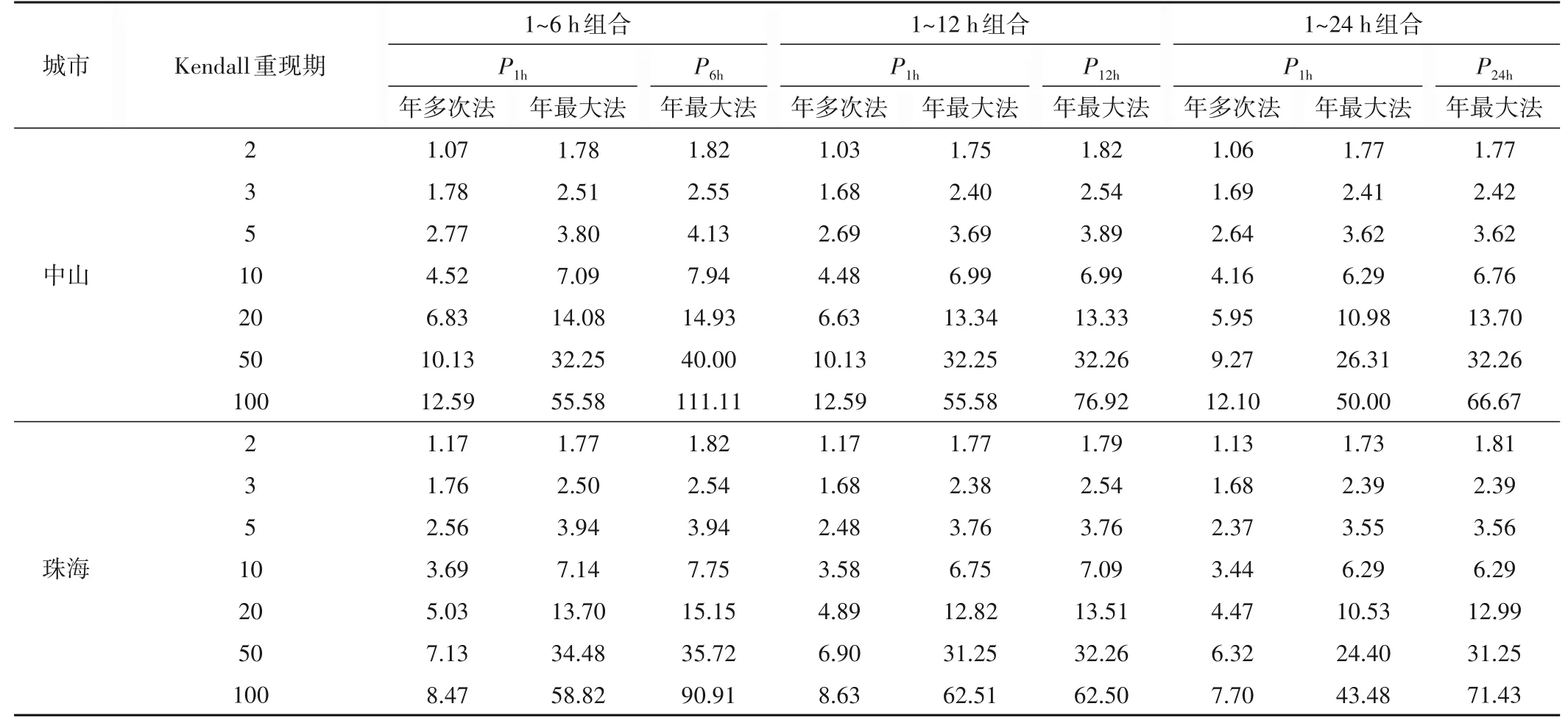
表8 給定Kendall重現期條件下的最可能排水排澇設計組合邊緣重現期 aTab.8 Marginal return periods of the most-likely design precipitation combinations with given Kendall return periods

5 研究小結

城市排水排澇系統是一個有機整體，只有科學聯合運用才能充分保障城市防洪排澇安全［27］。本研究以中山和珠海市為研究對象，基于Copula 原理和最可能法開展了城市排水排澇系統設計標準協調性研究，為科學選定城市設計排水排澇系統設計組合提供了有效的技術手段。本文主要研究結論如下：

（1）基于Copula 方法可有效構建不同歷時降水量序列的聯合概率分布，為實現城市排水排澇設計標準銜接提供了方法技術支撐；

（2）分別給定的排水排澇系統設計標準存在明顯的不協調性，以中山市主要城區設計值為例，排水系統設計標準偏低而排澇系統設計標準過高，采用本研究優化得到的最可能設計組合能夠更好地表征降水特性，為城市內澇防御體系建設提供了更為科學合理的參考依據。□