單級(jí)雙吸離心泵轉(zhuǎn)子系統(tǒng)的可靠性分析*

張 飛,權(quán)麗君

(1.江蘇聯(lián)合職業(yè)技術(shù)學(xué)院 徐州技師分院,江蘇 徐州 221000;2.蘇州大學(xué) 計(jì)算機(jī)科學(xué)與技術(shù)學(xué)院,江蘇 蘇州 215000)

0 引 言

隨著離心泵廣泛應(yīng)用,對(duì)其可靠性的提高、運(yùn)行能耗的降低不僅有巨大的經(jīng)濟(jì)價(jià)值,而且對(duì)提高國家泵產(chǎn)業(yè)發(fā)展水平具有重要意義[1，2]。

目前,離心泵朝著高轉(zhuǎn)速、高功率方向發(fā)展,對(duì)離心泵的轉(zhuǎn)子系統(tǒng)的穩(wěn)定性和可靠性提出了更高的要求[3]。因此,有必要對(duì)離心泵的轉(zhuǎn)子系統(tǒng)的穩(wěn)定性進(jìn)行研究。

單級(jí)雙吸泵轉(zhuǎn)子系統(tǒng)主要由:主軸、葉輪、聯(lián)軸器、軸承等機(jī)械零部件組成[4]。當(dāng)前,對(duì)于單級(jí)雙吸泵轉(zhuǎn)子系統(tǒng)的研究主要集中在軸承損傷、葉輪空蝕和磨蝕等方面。其中,虞烈等[5]通過理論分析,對(duì)軸承—轉(zhuǎn)子系統(tǒng)動(dòng)力學(xué)進(jìn)行了研究。尹江南等[6]對(duì)離心泵葉輪磨損破壞程度下的振動(dòng)特性進(jìn)行了分析,研究了葉輪空蝕后振動(dòng)特性。

然而,以上研究中對(duì)于離心泵轉(zhuǎn)子系統(tǒng)穩(wěn)定性的研究分析較少,大部分學(xué)者多是研究轉(zhuǎn)子臨界轉(zhuǎn)速對(duì)泵系統(tǒng)的影響。STOCKI R等[7]采用轉(zhuǎn)子系統(tǒng)前4階振型進(jìn)行了加權(quán)疊加,分析了轉(zhuǎn)子的不平衡量,減少了轉(zhuǎn)子系統(tǒng)不穩(wěn)定性。DIDIER J等[8]采用多項(xiàng)式混沌有限元的方法,對(duì)轉(zhuǎn)子系統(tǒng)進(jìn)行了可靠性研究。徐宇平等[9]通過對(duì)轉(zhuǎn)子流固耦合作用的研究,確保了轉(zhuǎn)子臨界轉(zhuǎn)速偏離設(shè)備自身旋轉(zhuǎn)速度,防止了轉(zhuǎn)子共振現(xiàn)象的產(chǎn)生。

在長期高速運(yùn)行過程中,單級(jí)雙吸泵由于轉(zhuǎn)動(dòng)軸設(shè)計(jì)、加工、安裝存在一定的誤差,軸倒角處會(huì)出現(xiàn)疲勞破壞產(chǎn)生裂紋,疲勞破壞的產(chǎn)生,輕則減少設(shè)備運(yùn)行時(shí)間,重則導(dǎo)致財(cái)產(chǎn)損失或人身傷害。

而目前對(duì)于泵的轉(zhuǎn)子臨界轉(zhuǎn)速的分析多是采用有限元方法。JAFARZADEH B等[10]采用了ANSYS有限元方法,對(duì)葉輪進(jìn)行了振動(dòng)特性以及強(qiáng)度問題的研究。BENRA F K等[11]采用了CFD方法,對(duì)單葉片進(jìn)行了雙向流固耦合,分析了其葉輪內(nèi)部的流場,并結(jié)合試驗(yàn)進(jìn)行了對(duì)比分析。

采用經(jīng)驗(yàn)法,通過增加軸的直徑以滿足其臨界轉(zhuǎn)速的設(shè)計(jì)要求,往往會(huì)帶來高昂的成本,造成不必要的浪費(fèi);合理增加軸的直徑不僅需要滿足其動(dòng)力學(xué)要求,也要滿足材料的力學(xué)強(qiáng)度要求。徐宇平等[12]采用了有限元方法對(duì)泵的轉(zhuǎn)子進(jìn)行了模態(tài)分析,以避免其發(fā)生共振。

目前,以數(shù)值分析和理論相結(jié)合的方式,在動(dòng)力學(xué)和靜力學(xué)方面綜合分析轉(zhuǎn)子系統(tǒng)穩(wěn)定性的研究較少。

本文主要通過數(shù)值分析和理論分析相結(jié)合的方法,對(duì)泵的轉(zhuǎn)子系統(tǒng)可靠性進(jìn)行研究,以滿足動(dòng)力學(xué)要求,防止共振的產(chǎn)生,同時(shí)滿足其材料力學(xué)強(qiáng)度的要求。

1 離心泵轉(zhuǎn)子結(jié)構(gòu)及其模型

1.1 基本參數(shù)及結(jié)構(gòu)

筆者所設(shè)計(jì)離心泵為單級(jí)雙吸離心泵,泵的轉(zhuǎn)軸和電機(jī)轉(zhuǎn)軸用膜片聯(lián)軸器進(jìn)行連接,泵體和電機(jī)通過基座與地基進(jìn)行螺栓連接。

離心泵基本計(jì)算參數(shù)如表1所示。

表1 基本計(jì)算參數(shù)

離心泵的轉(zhuǎn)子結(jié)構(gòu)主要包括軸、葉輪、軸套、軸承等部件,如圖1所示。

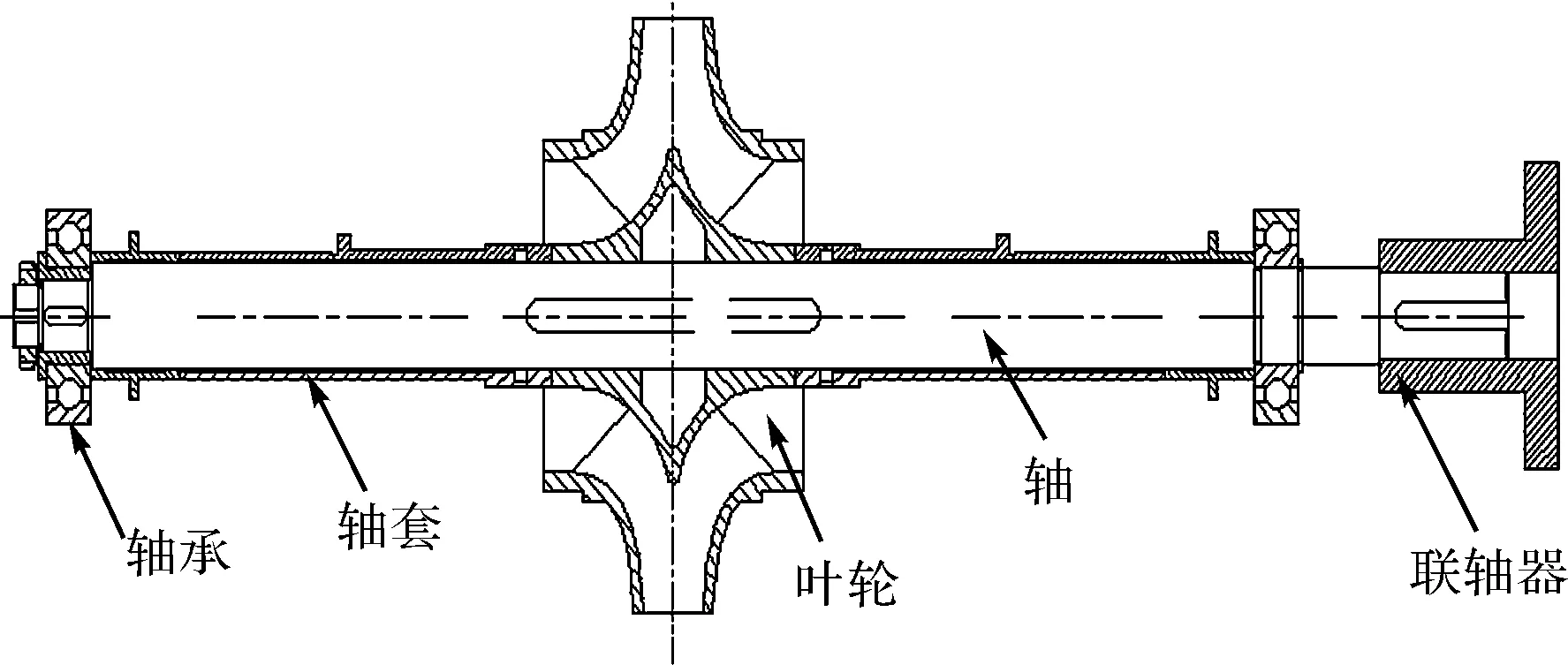
圖1 轉(zhuǎn)子系統(tǒng)結(jié)構(gòu)圖

1.2 幾何和有限元模型

筆者根據(jù)泵的葉輪和轉(zhuǎn)子相關(guān)圖紙,建立轉(zhuǎn)子三維幾何模型。在計(jì)算模型中,軸套、聯(lián)軸器以質(zhì)點(diǎn)的形式存在,軸承以支撐線形式存在,其目的是為了降低計(jì)算量,以增加計(jì)算的精度。

離心泵的轉(zhuǎn)子幾何模型如圖2所示。

圖2 轉(zhuǎn)子幾何模型

轉(zhuǎn)子的有限元模型圖如圖3所示。

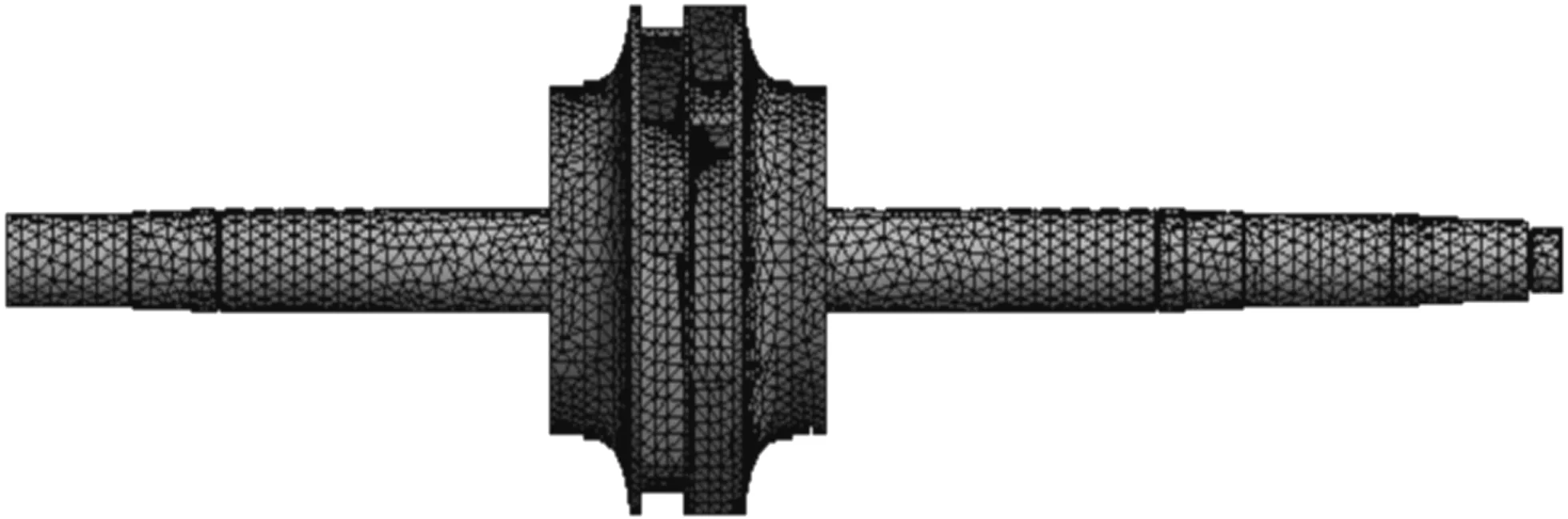
圖3 有限元模型圖

在圖3的有限元模型中,網(wǎng)格劃分為:單元體8.4×105,節(jié)點(diǎn)1.32×106,對(duì)模型進(jìn)行細(xì)化。

2 轉(zhuǎn)子系統(tǒng)的可靠性分析

此處筆者采用Workbench進(jìn)行轉(zhuǎn)子的靜力學(xué)分析。對(duì)轉(zhuǎn)子系統(tǒng)的強(qiáng)度進(jìn)行分析,主要是先計(jì)算轉(zhuǎn)子系統(tǒng)在運(yùn)行狀態(tài)下產(chǎn)生的實(shí)際工作載荷、變形、最大應(yīng)力、平均應(yīng)力等,然后通過數(shù)值模擬的方式,分析評(píng)判該轉(zhuǎn)子系統(tǒng)是否滿足設(shè)計(jì)的要求。

2.1 轉(zhuǎn)子系統(tǒng)應(yīng)力分析

由經(jīng)典力學(xué)理論[13]可知,轉(zhuǎn)子系統(tǒng)的結(jié)構(gòu)部件動(dòng)力學(xué)的方程為:

[M]{x″}+[A]{x′}+[N]{x}={F(t)}

(1)

式中:[M]—質(zhì)量矩陣;[A]—阻尼矩陣;[N]—?jiǎng)偠染仃?{x″}—加速度矢量;{x′}—速度矢量;{x}—位移矢量;F(t)—力矢量。

在設(shè)計(jì)機(jī)構(gòu)的分析過程中,往往把時(shí)間量忽略掉,于是上式可以簡化為:

[N]{x}={F}

(2)

此處筆者用質(zhì)量點(diǎn)代替聯(lián)軸器、軸套、軸承等部件,對(duì)轉(zhuǎn)子系統(tǒng)進(jìn)行靜力學(xué)分析;在葉輪處添加壓力載荷,在兩端軸承處施加位移約束,以計(jì)算在工作狀態(tài)下轉(zhuǎn)子系統(tǒng)的應(yīng)力狀態(tài)。

在工作狀況下,轉(zhuǎn)子的第一主應(yīng)力和第三主應(yīng)力的應(yīng)力圖如圖4所示。

(a)第一應(yīng)力 (b)第三應(yīng)力

接下來,計(jì)算轉(zhuǎn)子系統(tǒng)中軸上各個(gè)危險(xiǎn)點(diǎn)處應(yīng)力。

通過對(duì)轉(zhuǎn)子工作狀況下的應(yīng)力分析,可以發(fā)現(xiàn)在聯(lián)軸器處產(chǎn)生最大的膜應(yīng)力以及最大的彎應(yīng)力。根據(jù)設(shè)計(jì)要求,每個(gè)危險(xiǎn)位置處應(yīng)力應(yīng)該全部小于材料的許用應(yīng)力。

危險(xiǎn)處應(yīng)力結(jié)果如表2所示。

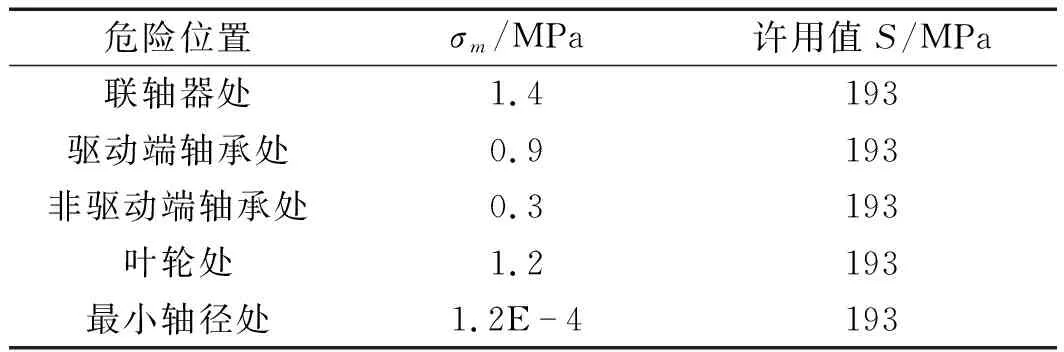
表2 危險(xiǎn)處應(yīng)力結(jié)果

由表2應(yīng)力結(jié)果分析可知,泵軸各個(gè)危險(xiǎn)處應(yīng)力滿足軸材料的許用應(yīng)力,泵軸強(qiáng)度滿足設(shè)計(jì)要求。

2.2 泵軸強(qiáng)度理論分析

雙吸泵轉(zhuǎn)軸的疲勞強(qiáng)度校核采用安全系數(shù)法,根據(jù)泵軸的尺寸,以及所受彎矩、扭矩,綜合考慮應(yīng)力集中等因素的影響,以及轉(zhuǎn)軸材料的疲勞極限,計(jì)算轉(zhuǎn)軸危險(xiǎn)截面處的疲勞安全系數(shù)是否滿足要求。軸的強(qiáng)度評(píng)定參照《機(jī)械設(shè)計(jì)手冊(cè)》[14]第2卷第6篇第1章。

根據(jù)經(jīng)驗(yàn)可知,泵軸最容易發(fā)生疲勞處為軸承所在軸段的倒角處,故筆者針對(duì)軸承段進(jìn)行疲勞校核。

根據(jù)《機(jī)械設(shè)計(jì)手冊(cè)》中的方法,計(jì)算結(jié)果如表3所示。

表3 轉(zhuǎn)軸的疲勞校核

根據(jù)計(jì)算結(jié)果可知,轉(zhuǎn)子系統(tǒng)中軸危險(xiǎn)截面的安全系數(shù)大于許用安全系數(shù)時(shí),轉(zhuǎn)子系統(tǒng)滿足強(qiáng)度的要求。

2.3 泵軸臨界轉(zhuǎn)速分析

在不考慮摩擦以及外載荷的情況下,離心泵轉(zhuǎn)子系統(tǒng)臨界轉(zhuǎn)速采用有限元的方法進(jìn)行計(jì)算,用相似的方法求特征值和特征向量[15]:

Mx″(t)+Nx(t)=0

(3)

式中:M,N—系統(tǒng)的整體質(zhì)量矩陣、剛度矩陣;x″(t),x(t)—有限元節(jié)點(diǎn)加速度、位移;0—零矩陣。

假定式中為簡諧函數(shù)形式,并考慮其獨(dú)特性,其函數(shù)表示為:

det|K-ω2M|=0

(4)

然后求出該公式中的特征值ωi和特征向量φi;每一個(gè)特征值對(duì)應(yīng)一個(gè)特征向量,形成一個(gè)振動(dòng)形式,即:

(5)

式中:fi—第i階固有頻率。

在運(yùn)行過程中,離心泵的整個(gè)轉(zhuǎn)子系統(tǒng)以及連接的電動(dòng)機(jī)會(huì)產(chǎn)生不同頻率的振動(dòng),當(dāng)轉(zhuǎn)子振動(dòng)頻率與固有頻率相一致時(shí),會(huì)產(chǎn)生共振現(xiàn)象,共振會(huì)增強(qiáng)整體的振動(dòng)水平,振動(dòng)的增強(qiáng)會(huì)導(dǎo)致轉(zhuǎn)子系統(tǒng)被破壞,導(dǎo)致雙吸泵性能下降以及安全性降低。

為了增強(qiáng)轉(zhuǎn)子系統(tǒng)的穩(wěn)定性,轉(zhuǎn)子系統(tǒng)需要避開轉(zhuǎn)軸的固有屬性。筆者通過對(duì)轉(zhuǎn)子系統(tǒng)的模態(tài)分析計(jì)算可知,臨界轉(zhuǎn)速要大于轉(zhuǎn)子轉(zhuǎn)速1.2倍[16]。

轉(zhuǎn)子系統(tǒng)的一階臨界轉(zhuǎn)速為扭轉(zhuǎn)模態(tài),二階、三階、四階模態(tài)為橫向模態(tài)分析,轉(zhuǎn)子臨界轉(zhuǎn)速如圖5所示。

(a)一階模態(tài)

各個(gè)臨界轉(zhuǎn)速值如表4所示。

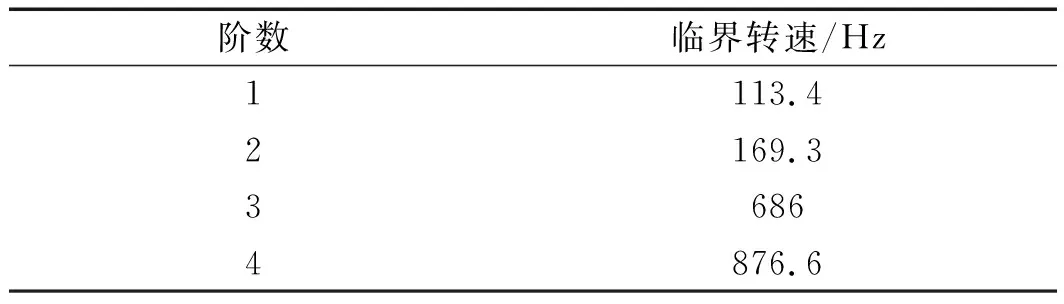
表4 轉(zhuǎn)子臨界轉(zhuǎn)速值

由動(dòng)力學(xué)模態(tài)分析可知,由于轉(zhuǎn)子系統(tǒng)剛度較弱,在轉(zhuǎn)子的一階臨界轉(zhuǎn)速出現(xiàn)扭轉(zhuǎn)模態(tài)。

該單級(jí)雙吸泵固有頻率為48.3 Hz(2 900/69=48.3 Hz),一階臨界轉(zhuǎn)速113.4 Hz>48.3 Hz,當(dāng)一階臨界轉(zhuǎn)速大于1.2倍固有頻率時(shí),不會(huì)產(chǎn)生共振現(xiàn)象。

3 泵軸臨界轉(zhuǎn)速理論分析

目前,對(duì)于泵軸臨界轉(zhuǎn)速的分析多是采用數(shù)值分析的方法;為了保證結(jié)果的準(zhǔn)確性,往往采用機(jī)械設(shè)計(jì)手冊(cè)理論公式進(jìn)行驗(yàn)算,保證臨界轉(zhuǎn)速結(jié)果的正確,提高轉(zhuǎn)子臨界轉(zhuǎn)速模擬計(jì)算結(jié)果的可靠性。

臨界轉(zhuǎn)速理論值大小與圓盤質(zhì)量、軸質(zhì)量、軸形狀等因素有關(guān),需要同時(shí)考慮不同因素對(duì)轉(zhuǎn)子系統(tǒng)的綜合影響,理論值在工程實(shí)際運(yùn)用中較為保守。因此,根據(jù)不同的設(shè)計(jì)要求,筆者建立計(jì)算模型,根據(jù)公式計(jì)算出泵軸轉(zhuǎn)子系統(tǒng)臨界轉(zhuǎn)速的近似值。

轉(zhuǎn)子系統(tǒng)臨界轉(zhuǎn)速的計(jì)算公式如下:

(6)

式中:m1—葉輪質(zhì)量,kg;m0—軸的質(zhì)量,kg;E—軸材料彈性模量,Pa;J—軸的截面慣性矩,m4;γ—支座形式系數(shù);β—集中質(zhì)量m1轉(zhuǎn)換為分布質(zhì)量的折算系數(shù)。

該理論公式對(duì)轉(zhuǎn)子系統(tǒng)一階、二階臨界轉(zhuǎn)速較為適用,大于二階轉(zhuǎn)速時(shí)誤差較大。

臨界轉(zhuǎn)速有限元計(jì)算和理論計(jì)算值如表5所示。

表5 轉(zhuǎn)子臨界轉(zhuǎn)速對(duì)比表

從表5中可看出,臨界轉(zhuǎn)速的計(jì)算值大于有限元計(jì)算值。由于軸的結(jié)構(gòu)變化、軸材料以及各個(gè)轉(zhuǎn)子部件動(dòng)態(tài)特性的不確定性導(dǎo)致了兩者結(jié)果的差異,但兩者結(jié)果的誤差均在合理且可接受的范圍內(nèi)。因此,該有限元分析的結(jié)果是合理的。

4 結(jié)束語

本文主要通過數(shù)值分析和有限元分析相結(jié)合的方法,對(duì)單級(jí)雙吸泵的轉(zhuǎn)子系統(tǒng)可靠性進(jìn)行研究,以滿足其動(dòng)力學(xué)要求,防止轉(zhuǎn)子系統(tǒng)共振的產(chǎn)生,同時(shí)滿足其材料力學(xué)強(qiáng)度的要求。

通過分析得出如下結(jié)論:

(1)通過Workbench靜力學(xué)分析以及強(qiáng)度理論公式綜合分析發(fā)現(xiàn),轉(zhuǎn)子系統(tǒng)強(qiáng)度滿足材料的力學(xué)性能,且危險(xiǎn)截面安全系數(shù)大于需用安全系數(shù);

(2)對(duì)轉(zhuǎn)子系統(tǒng)進(jìn)行模態(tài)分析和理論分析后發(fā)現(xiàn),當(dāng)轉(zhuǎn)子剛度較低時(shí),一階臨界轉(zhuǎn)速為扭轉(zhuǎn)模態(tài),且轉(zhuǎn)子系統(tǒng)一階臨界轉(zhuǎn)速遠(yuǎn)大于實(shí)際轉(zhuǎn)速的1.2倍,因此系統(tǒng)不會(huì)發(fā)生共振現(xiàn)象;

(3)通過對(duì)離心泵轉(zhuǎn)子系統(tǒng)進(jìn)行模擬計(jì)算和理論公式計(jì)算,保證了結(jié)果的準(zhǔn)確性,因此,可以提高產(chǎn)品的安全性。

筆者通過對(duì)轉(zhuǎn)子系統(tǒng)的研究,發(fā)現(xiàn)泵體內(nèi)流場的不穩(wěn)定性對(duì)轉(zhuǎn)子穩(wěn)定具有一定的影響。在后續(xù)的研究過程中,筆者將采用FLUENT方法,來綜合分析流場對(duì)離心泵轉(zhuǎn)子系統(tǒng)的影響。