平面向量的幾類運算問題

巨小鵬

(陜西省漢中市龍崗學校 723102)

平面向量是代數、幾何和三角函數之間的橋梁，集數與形于一體的一種工具.從向量的運算角度看，向量具有較好的代數結構；從幾何角度看，向量是空間最基本原始的幾何量.這使得向量運算都有著其幾何意義，運算律也具有豐富的幾何內涵，如向量的加法用幾何語言描述就是三角形法則或平行四邊形法則；向量加法的交換律是平行四邊形定理的向量表述形式；數乘運算的分配律是相似三角形定理的代數形式；數量積的分配律也是勾股定理代數化的一種表達形式等.平面向量運算內容包括平面向量的加減運算、數乘運算、數量積、向量的模、運算法則、運算性質和幾何意義等.

一、 圖形形式的運算問題

A.(-2,6) B．(-6,2) C．(-2,4) D．(-4,6)

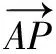
分析3 坐標法也可以，較簡單在此不贅述.

評析以正六邊形為載體，考查有關平面向量數量積的取值范圍，涉及到的知識點有向量數量積的運算及其幾何意義.

二、符號形式的運算問題

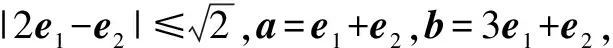
評析考查了利用模求向量數量積、利用向量數量積求向量夾角、利用函數單調性求最值，考查轉化與化歸思想，考查數學運算、數學建模等學科素養，解題關鍵是合理轉化，應用函數求最值，特別注重基礎.

三、坐標形式的運算問題

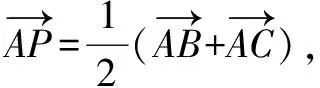
評析考查平面向量的模和數量積的計算，建立平面直角坐標系，求出點P的坐標是解答的關鍵.

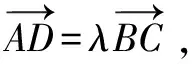
評析考查平面向量數量積的計算，考查平面向量數量積的定義與坐標運算.坐標法明顯比較好，運算更加流暢，也容易想到.

四 、平面向量與平面幾何的綜合問題

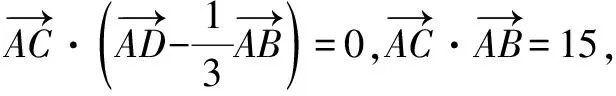
A．8 B．6 C．4 D．2

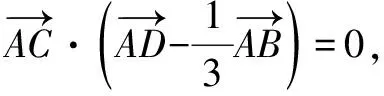
不管哪種類型的題，方法的選取無非就是定義法、基向量法、坐標法、幾何意義法，必要的時候構造方程、構造三角形、解三角形等.在學習過程中更要重視一題多解和一解多題的反思性總結.