挖掘理想重建圖像自相似性的超分辨率

李鍵紅 吳亞榕 詹瑾

摘 ? 要：為了解決圖像超分辨率過程中訓練步驟對海量數據的過于依賴、先驗泛化能力不強等問題，進一步提高重建圖像的質量，提出了一種新的圖像超分辨率算法. 首先對圖像自相似性理論進行擴展，指出理想重建圖像自相似性表現極為強烈，而受降質因素干擾的重建圖像自相似性則會明顯減弱. 本文將這一規律視為先驗，通過構建聯合高斯混合模型對其進行描述，這使得每個重建圖像片的自相似性都能夠用一個特定的高斯分布進行刻畫，最后算法以迭代的方式分片重建整幅高分辨率圖像. 在為每個高分辨率圖像片建模的過程中，為了使訓練樣本具有較強的一致性，僅使用輸入圖像中與其空間位置相近的圖像片進行訓練. 該算法避開了易于引入誤差的最近鄰域查找步驟，且成本函數存在解析解. 實驗表明該算法重建圖像清晰、自然，重建結果中的顯著邊緣和紋理結構都得到了有效保持，正確的高頻信息得到了明顯恢復. 在將BSD500部分數據集放大3倍的實驗中，本文算法的PSNR平均值高于MMPM算法0.529 db，SSIM平均值高于MMPM算法0.030.

關鍵詞：單幀圖像超分辨率;自相似性;高斯混合模型;概率密度函數;最大后驗概率;維納濾波解

中圖分類號：TP391.4 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標志碼：A

Image Super-resolution by Exploiting

Self-similarity of Ideal Reconstruction

LI Jianhong1，WU Yarong2，ZHAN Jin3

（1. School of Information Science and Technology，Guangdong University of Foreign Studies，Guangzhou 510006，China;

2. School of Mechatronic Engineering，Zhongkai University of Agriculture and Engineering，Guangzhou 510225，China;

3. School of Computer Science，Guangdong Polytechnic Normal University，Guangzhou 510665，China）

Abstract：To solve the problems such as over-reliance on massive data and weak prior generalization ability in the training procedure of image super-resolution，thus further to improve the quality of reconstructed high resolution image，a new image super-resolution algorithm was proposed. This paper firstly extends the theory of image self-similarity and points out that the self-similarity of ideal reconstruction image is extremely strong，but this property can be sharply weakened when the reconstructed image is attacked with some degradation factors. Then this discovery is considered as a prior and described by constructing a joint Gaussian mixture model，so that the self-similarity of each reconstructed image patch in the prior term can be represented by a specific Gaussian distribution. For maintaining the training samples' consistency，only the image patches extracted in the input image closed to its spatial position are permitted to join in the modeling process for each high-resolution image patch. This style can avoid the step of finding the nearest neighbors which is liable to introduce errors. Finally，the whole high-resolution image can be reconstructed patch-wise in an iterative way. Extensive experiments demonstrate that the reconstructed images generated by the proposed algorithm are clear and natural，in which the salient edges and texture structures are effectively preserved，and the correct high-frequency information is recovered. The 3× super-resolution experiment in BSD500 shows that the average PSNR is higher 0.529 db than the state-of-the-art algorithm MMPM，and the average SSIM is 0.030 higher than ?MMPM.

Key words：single image super-resolution;self-similarity;Gaussian mixture model;probability density function;maximum posterior probability;Wiener filter solution

圖像超分辨率是指通過軟件計算的方式處理一幅低分辨率圖像，估計對應高分辨率圖像的技術. 它是常見的信號編輯形式，是低成本獲取高分辨率圖像的主要手段，廣泛應用于空間遙感、視頻監控及數字家庭等場景. 近年來，由于潛在廣闊市場地驅動，以及飛速發展的軟/硬件支持，超分辨率取得了顯著進展，已成為學術界討論的熱點話題.

一般來說，根據低分辨率圖像反推對應的高分辨率圖像是一個典型的病態逆問題[1]. 為了得到清晰可靠的重建圖像，人們通常引入先驗對高分辨率圖像的重建過程進行約束，先驗恰當與否和重建圖像質量密切相關. 根據引入先驗形式的不同，超分辨率算法大致可分為插值法、重建法和學習法三類.

基于學習的方法指的是借助外界高分辨率圖像建立訓練集，并利用訓練集歸納低/高分辨率圖像間的映射，使先驗以隱含的方式包含在映射中. 這類方法能夠有效地恢復成像過程中丟失的高頻信息，生成在輸入圖像中觀察不到的細節，從而使其倍受重視，成為超分辨率技術的主流. Yang等[2]將稀疏表示的思想引入到超分辨率中，用不同尺度的圖像片聯合訓練字典. 但該方法導致字典中與輸入圖像片差異很大的“原子”參與計算，在重建結果中產生噪聲. Timofte等[3]將稀疏表示與鄰域嵌入相結合，對每一個低分辨率圖像片，在字典中查找距離它最近的“原子”，利用該“原子”在字典中的k近鄰構建矩陣算子. 在此基礎上，Timofte等[4]進一步挖掘初始的訓練圖像，再次提升此算法的性能. 深度學習在超分辨率中也得到了廣泛應用[5-7]. ?但這類算法通常需要借助圖形處理單元（Graphics Processing Unit，GPU）訓練海量圖像，以確定神經節點的權重. 在訓練過程中，先驗不易在此類方法中發揮作用，限制了重建圖像的質量以及重建過程的穩定性.

近年來，自相似性在圖像處理中得到了廣泛應用[8-13]. 這一性質指的是當從局部入手（即圖像中的一個5 × 5、7 × 7或其他小尺寸的圖像片）對圖像進行考察時，會在這幅圖像自身或更高＼低尺度內的其他位置發現與之尺寸相同、包含內容極其相似的圖像片[8-10]. ?基于自相似性的超分辨率算法把輸入圖像視作樣本，訓練模型、估計高分辨率圖像. Glasner等[8]提出一個整合式的超分辨率框架，把相似圖像片視為同一場景的不同視圖，整合多幀圖像超分辨率和基于學習的超分辨率兩種思想對圖像進行放大. 然而對于自相似性弱的圖像，某些圖像片查找到的最近鄰域會與之存在較大差異，使重建結果中出現噪聲，甚至引入錯誤高頻. 另外，該方法需要在輸入圖像的多尺度中搜索最近鄰域，算法相對耗時. Freedman等[14]經驗性地指出自然圖像中幾乎所有圖像片在其自身或較低尺度內的最近鄰域，只需在該圖像片所在位置附近檢索就能查找到. Yang等[15]進一步在理論上通過數學推導對這一性質加以證明. 這使得查找最近鄰域消耗的時間顯著縮短，然而由于使用的訓練樣本數量有限，導致此類方法的重建圖像在邊緣位置過于銳利，看上去不夠自然. 為了解決此種“小樣本”問題，He等[16]引入高斯過程回歸，在每個圖像區域內構建樣本集合、訓練參數. 但該算法沒有挖掘區域間的關聯關系，使得重建結果中的顯著邊緣產生變形，附近存在噪聲. 基于同樣的目的，Huang等[17]通過變換矩陣對輸入圖像片進行特定的幾何變形，不僅擴展了最近鄰域的查找空間，而且使圖像片間的匹配更加準確，提高了重建圖像質量. 該算法對于直線條居多、無復雜紋理的“建筑場景”效果較好，但對包含復雜紋理的“自然風光”而言，由于幾何變形導致了紋理結構的失真，在重建圖像的對應區域會出現偽影.

另外，自相似性先驗表達式在眾多領域也得到了應用[18-21]. 自相似性先驗表達式通常會與其他先驗如局部平滑先驗、稀疏先驗、低秩先驗等結合使用. 算法一般先查找若干最近鄰域，然后借助這些相似圖像片的稀疏系數相似或相似圖像片構成的矩陣具有低秩結構等特點設計先驗表達式. 為了確定模型參數，這些算法仍需外界圖像參與訓練. 成本函數中的先驗表達式由多項構成，此類算法求解計算復雜、耗時，不易在實際中使用.

本文挖掘理想高分辨率圖像的自相似性，提出了一種簡單、高效的超分辨率算法，創新點如下：

1）拓展了自相似性概念. 重建高分辨率圖像越清晰，它體現出的自相似性就越強烈;當高分辨率圖像中存在噪聲、模糊等因素影響或缺失高頻信息時，它所體現出的自相似性會明顯減弱. 基于此性質，提出了一種新的先驗，通過對低分辨率圖像進行建模、推導后發現，滿足這一先驗的重建圖像，它的任意圖像片都服從于某個特定的高斯分布.

2）設計了一個迭代框架，在每次迭代中，使用前次估計的高分辨率結果結合輸入圖像構造訓練集合. 對每個圖像片，考慮到圖像內容的連貫性，該算法使用輸入圖像中與之空間位置較近的圖像片集合構造訓練樣本，并采用快速更新的方式確定模型參數. 實驗表明，該算法對于恢復圖像高頻細節，保持圖像紋理結構等有顯著優勢.

3）該算法簡單、高效，不僅無需外界樣本參與，而且避開了耗時的最近鄰域查找步驟. 另外，在高斯混合模型建模、參數更新的過程中僅使用少量高斯成分，成本函數方程存在閉合解. 更為重要的是該算法能夠根據輸入圖像的不同而自動進行模型參數的調整，使得該算法更為魯棒，易于擴展到圖像去噪、復原等其他領域.

1 ? 相關工作

圖像在成像過程中會受到相對運動、聚焦失準等復雜因素干擾，很難找到一個完美的數學模型來精確刻畫成像過程，因此在實際應用中，對于圖像的超分辨率問題，通常用一個線性系統對整個成像過程進行模擬[1]：

Y = DHX + n， ? ? ? ? ? ? ? ? ? ? ? ? ? （1）

式中：X∈RMN和Y∈RMN/s2 是來自同一場景，但分辨率不同的兩幅圖像，X是未知的高分辨率圖像;Y是人眼能夠觀察得到的低分辨率圖像，（為了操作方便，此時的圖像X和Y已通過字典排序的方式轉換成向量的形式，M代表圖像的像素點行數，N代表圖像的像素點列數，R表示像素點的亮度取值自實數空間范圍，s表示X和Y間的縮放倍數）;矩陣D和H分別對應成像過程中的下采樣和低通濾波操作;n∈RMN/s2 是成像過程中產生的加性高斯白噪聲，滿足n ～ N（0，σ2I），σ為描述噪聲等級的標準差，I為單位矩陣. 圖像X和Y的尺寸分別為M × N和M/s × N/s. 顯然對于一幅低分辨率圖像Y而言，X存在著無窮多的解與之匹配. 為了得到一個滿意的解X*，先驗知識的引入就變得尤為關鍵. 一般情況下這類問題可以描述為一個最大后驗概率方程：

X* = ‖Y - DHX‖22 + λP（X） ? ?（2）

式中：‖Y - DHX‖22 為保真項，使重建高分辨率圖像經過成像模型處理后，與輸入的低分辨率圖像盡可能相似;P（X）為先驗項，用于確保高分辨率圖像滿足先驗P的約束;λ = σ2/η2是兩項間的平衡系數（η是尺度縮放因子）. 然而圖像就其整體而言內容豐富、結構多樣，很難找到統一形式的先驗. 但當從小局部（如5×5、7×7的圖像片）進行觀察時，圖像片內容單一，有極強的規律性，易于描述. 因此通常從圖像片出發對先驗項建模，將P（X）表述為：

式中：Pi為抽取矩陣，負責抽取未知高分辨率圖像X中的i第個圖像片，即Pi X = xi，xi∈Ra2 ，a為圖像片的尺寸;ρ（xi）為第i個圖像片xi的先驗表達式，它的具體表示形式因選擇先驗的不同而不同，對應成本函數的求解過程也不一樣. 一般而言，這類問題的成本函數是非凸的，直接求解會非常困難. 常見的思路是為變量xi引入輔助變量，使用“半二次分裂”（Half Quadratic Splitting，HQS）算法求解[22].

高斯混合模型（Gaussian Mixture Model，GMM）因其思想簡單、推導方便、能準確描述任意概率密度函數等特點備受研究人員青睞. 近年來，將GMM作為先驗形式在計算機視覺、圖像處理等領域得到了廣泛應用，在圖像分割、恢復、視頻壓縮等方向展現出了極高的效率[23-24]. 它的基本形式為：

式中：z∈Rd是一個d維隨機向量;K為高斯混合模型高斯成分的個數;參數πk、 μk和∑k分別表示第k個高斯成分的權重系數、均值向量和協方差矩陣. 第k個高斯成分的表達式為：

根據高斯混合模型的定義可知，πk = 1，對于參數集合{πk，μk，∑k}K ? k=1的估計，通常采用期望最大化（Expectation Maximization，EM）進行.

與本文算法在形式上相似，但又存在本質差異的工作包括PLE[25]、EPLL[26]、LINE[27]、J-GMM[28]和 MMPM[29]. 其中 EPLL、J-GMM 均使用高斯混合模型對外界海量圖像片進行建模，進而假定未知圖像片由混合模型中的某個高斯成分生成，然后通過最大后驗概率估計將該成分找到，最后使用均值向量和協方差矩陣計算維納濾波解. 然而圖像中存在大量的圖像片，并不服從這一假設. 它們需要借助多個高斯成分或混合模型之外的新成分才能準確生成. 這使得信號估計過程中，僅使用某個高斯成分的均值向量和協方差矩陣計算的維納濾波解不準確，導致重建圖像中存在噪聲和模糊現象. MMPM算法與J-GMM算法步驟相同，區別在于它使用學生氏分布替換混合模型中的高斯成分，在重建結果中同樣存在少量噪聲和模糊. PLE和LINE算法也從上述假設出發，先查找待恢復圖像片在訓練集中的最近鄰域，再通過這組最近鄰域直接構建混合模型中能夠生成對應圖像片的高斯成分. 然而查找最近鄰域步驟過于耗時，同時這種硬閾值聚類的形式減弱了訓練樣本間的一致性，導致高斯成分所涉及到的參數不準確，在重建結果中易出現噪聲.

本文僅使用輸入圖像構建訓練集，對每一個待超分辨率的圖像片，在訓練集中選擇空間位置相近的圖像片進行聯合高斯混合模型訓練，利用高斯混合模型，得到每一個未知的高分辨率圖像片都服從一個“特定”的高斯分布這一結論. 最后利用混合模型之外某個高斯分布的均值向量和協方差矩陣估計對應的高分辨率圖像片.

2 ? 理想重建圖像自相似性超分辨率

2.1 ? 訓練集構造

自相似性是圖像自身固有的一種性質，它指的是在圖像中任意抽取的圖像片會在這幅圖像自身其他位置或其他尺度內重復出現的現象. 在這一基礎上，對自相似性進行擴展. 通過進一步實驗，發現在超分辨率工作中，越是清晰的高分辨率重建圖像，圖像片重復出現的能力就越強烈;但在含有噪聲、模糊或缺失高頻信息的高分辨率重建圖像中，圖像片的重現能力明顯減弱. 如圖1所示，中間的小圖像為輸入低分辨率圖像，圖1為其不同的超分辨率版本. 對于4幅圖像中某個位置的圖像片，在對應的低分辨率圖像中查找最近鄰域，可以發現這4個來自不同版本同一位置的圖像片，在低分辨率圖像中的最近鄰域都能夠在這個位置附近找到. 更為重要的是：只有在理想超分辨率圖像中的圖像片，它找到的最近鄰域才與之在外觀上相似;其他版本中這個圖像片找到的最近鄰域，在外觀上都與之存在差異. 在BSD500數據集中進行類似的實驗，發現絕大多數的圖像都存在上述特點. 因此可以認為在超分辨率算法中，重建高分辨率圖像越清晰，它所體現出的自相似性越強烈;但當高分辨率重建結果中存在噪聲、模糊或缺失高頻信息等因素時，它所體現出的自相似性會顯著減弱.

借助這一規律，提出一種新的超分辨率算法，采用迭代的方式，用輸入圖像Y估計對應高分辨率圖像X. 算法迭代框架如圖2所示，假定前一次迭代估算的高分辨率圖像X未滿足算法要求，將其視為理想高分辨率圖像的低頻版本，替換當前低頻圖像X′，實現了X′的更新，然后將X′使用雙三次方法下采樣 s倍，得到與輸入圖像同尺寸的低分辨率圖像Y′. 此時X為未知的高分辨率圖像，X和Y′可以視為X和X′通過成像模型處理的低分辨率版本，X′和Y′可以視為X和Y的低頻版本.

根據上述的圖像自相似性擴展規律可知，如果 X和X′相對于Y和Y′足夠清晰，那么在X和X′中抽取的圖像片Xi和X′i（xi∈Ra2 ，a為抽取圖像片的尺寸），應該能夠在其對應的低分辨率版本Y和Y′中找到重現，即存在圖像片yj和y′j，其外觀與xi和x′i高度相似，即圖像片xi和x′i在Y和Y′的圖像片聯合的概率密度函數中以最高的概率存在.

基于上述分析，將圖像的超分辨率問題構造如下：對于未知的高分辨率圖像片xi，先構造訓練數據集，抽取Y和Y′中的圖像片進行連結，得到訓練數據集{yj;y′j}，其中yj和y′j表示分別從Y和Y′中抽取的第j個圖像片. 將理想的高分辨率圖像X中抽取的圖像片xi和缺失高頻成分的高分辨率圖像X′中對應的圖像片x′i相連結，得到向量[xi;x′i]. 根據圖像的自相似規律可知：[xi;x′i]在訓練集合{[yj;y′j]}中的概率密度函數中應以最高的概率存在. 考慮到圖像內容本身有很強的連貫一致性，為了使得到的概率密度函數更準確，在構造xi的訓練集時，我們在Y和Y′中分別設定一個w×w的滑動窗口，其當前中心位置與xi位置相同，僅將窗口中的圖像片集合作為xi的訓練集，窗口外的內容不參與圖像片xi的計算. 考慮到窗口內能夠抽取的圖像片有限，參與計算的樣本可能不足，我們將窗口中的內容進行旋轉和鏡像操作，并從這些旋轉和鏡像圖像對應的窗口中抽取圖像片以此擴充訓練樣本.

2.2 ? 自相似先驗設計

對于每個圖像片xi所使用的訓練集合{[yj;y′j]}，yj∈Ra2 ，y′j∈Ra2 ，引入高斯混合模型逼近訓練集的概率密度函數，如式（6）所示：

Pyjy′j=πk Nyjy′jμykμy′k，∑yyk ?∑yy′k ?∑y′yk ? ?∑y′y′k ? ?（6）

式中：向量μk = [μyk;μy′k]和矩陣∑k = [∑yyk，∑yy′k ?，∑y′yk ? ，∑y′y′k ? ]分別表示第k個高斯混合模型的均值向量和協方差矩陣，內部的元素向量μyk、 μy′k和矩陣∑yyk、∑y′y′k ? 分別表示訓練集合聯結前的圖像片向量集合{yj}和{y′j}在高斯混合模型聚類結果中第k簇兩組圖像片的均值向量和協方差矩陣，∑yy′k ?、∑y′yk ? 是第k簇訓練樣本中兩組圖像片的協方差矩陣，按照協方差矩陣的定義∑yy′k ? = （∑y′yk ? ）T（T表示對矩陣進行轉置操作），πk表示高斯混合模型中第k個高斯成分的權重. 式（6）中高斯混合模型參數集Ω = {πk，μk，∑k}K ? k=1的求解采用EM算法，分為E步和M步迭代進行估計.

然而，在實際執行過程中，如果對每一個高分辨率圖像片的估計都使用EM算法進行模型訓練，會導致算法的執行異常復雜，不能在可容忍時間范圍內結束計算. 為了解決這一問題，使用參數自動更新的EM算法進行模型訓練[30]. 由于相鄰兩個高分辨率圖像片存在內容重復，其對應的參數間有著密切的關系，后一個圖像片的參數集能夠借助前一個圖像片模型的訓練結果，僅使用新出現的樣本對參數集進行更新，既能夠快速完成訓練，又能夠保證模型的準確程度. 圖3中算法詳細地列出了模型參數更新的具體步驟.

Input：LR image Y;upsampling factor s

Output：Reconstructed HR image X

X = upsampling（Y，s）% bicubic

For t = 1 ： T do

X′ = X;

Y′ = downsampling（X′，s）;% bicubic

{π′k，μ′k，Σ′k} = initialize（Y，Y′）;% with EM

For each patch x′iextracted from X′

{yj，y′j} = training（Y，Y′）;

zl = [yl;y′l];% l = 1，2，…，M

For k = 1 ∶ K

For each new example zi

γ（k|zi，Ω） = ;

nk = γ（zi | μk，∑k）;

End For;

πk = [απ（nk /M） + （1 - απ）π′k]nk;

μk = αμπk zi /πk +（1 - αμ）μ′k;

Σk = αΣ?+ （1 - αΣ）∑′k

End For

Compute μ Xi and ∑ Xi with the GMM

parameters Ω = {πk，μk，∑k};

Estimate xi with μ Xiand ∑ Xi;

End For

Estimate the HR image X with {xi}N ?i=1;

End For

Return X

對于未知的高分辨率圖像X，把從中抽取的圖像片xi和在圖像X′中相同位置的圖像片 進行連結，得到對應的連結向量[xi ;x′i]，它在訓練集合的概率密度函數中存在的概率可以表示為：

進而可以發現xi 的條件概率服從一個特定的高斯分布：

P（xi |x′i，Ω）～N（xi | μXi，∑Xi） ? ? ? ? （8）

式中：μXi為這個高斯分布的均值向量，∑Xi為這個高斯分布的協方差矩陣，它們的表達式分別為：

其中Δik和（Δik）2分別為式（9）和式（10）中的公共因子，Δik的具體表達式為：

事實上Δik描述了圖像片x′i由當前所訓練的高斯混合模型中第k個高斯成分生成的后驗概率. 在實驗中發現，在高斯成分個數K確定的前提下，對于絕大多數的圖像片而言，集合{Δik}是稀疏的，即絕大多數Δik值為0，或非常接近0，尤其是混合模型中高斯成分的個數K = 3時，僅使用Δik取最大值時所對應的高斯成分，即第Δik個高斯成分，可準確表示μXi和∑Xi（在實驗部分，將進一步對圖像片的該性質進行說明），Δik的表達式為：

式（12）表示在第i個圖像片所對應的高斯混合模型分布中，第k*i個高斯成分對應的公共因子Δik*i值最大，N表示在圖像X中抽取圖像片的總數. 因此圖像片xi對應的特定高斯分布的均值向量 μXi和協方差矩陣∑Xi可以近似表示為：

μXi≈ μyk*i +∑yy′k*i ? （∑y′y′k*i ? ）-1（x′i - μy′k*i） ? ?（13）

∑Xi≈∑yk*i -∑yy′k*i ? （∑y′k*i ）-1∑y′yk*i ? ? ? ? ?（14）

通過上述推導，理想的重建圖像中任意抽取的圖像片x其自相似先驗的具體表達式為：

ρ（x） = （xi ?- μXi）T∑-1Xi （xi ?- μXi） ? ? ?（15）

進而，整幅圖像的自相似性先驗表示為：

P（X） = （Pi X - μXi）T∑-1Xi （Pi X - μXi） ? ? ?（16）

式中：N為在未知超分辨率圖像X中抽取的圖像片數量;Pi為一個預先設定的抽取矩陣，用于抽取X中的第i個圖像片. 由于式（15）（16）中所描述的先驗知識是對未知的高分辨率圖像中的每一個圖像片在較低尺度中重現的概率進行估計，是對理想重建高分辨率圖像的一種刻畫，因此將這一先驗知識稱為理想重建圖像自相似先驗.

2.3 ? 高分辨率圖像重建

先驗的表達式確定后，該算法的成本函數就能夠通過這個具體先驗表達式進一步構造出來. 在本文的超分辨率重建算法中，要求得到的超分辨率重建結果在滿足理想重建圖像自相似性先驗的同時，重建的高分辨率圖像在通過成像式（1）處理后，還應與輸入的低分辨率圖像盡可能的相似. 為了兼顧這兩個要求，通過加權求和的形式整合這兩項表達式，將該算法的成本函數設計為：

其中第一項稱為保真項，它能夠使得估計的高分辨率圖像X在經過退化模型處理后得到的結果與觀察圖像盡可能的一致;第二項是先驗項，用于約束重建的高分辨率圖像滿足尺度間自相似性. ?用于兩項間的權衡. 這個成本函數的求解較為簡單，可直接對式（17）進行求導，并令導數為0，即可得到關于X的表達式，進一步整理可以得到超分辨率圖像的最終估計結果：

然而在重建高分辨率圖像X表達式的計算過程中，需要操作的矩陣通常具有極大的規模，如下采樣矩陣D、濾波矩陣H和抽取矩陣Pi，這樣的計算方式占用內存空間過大、耗時且復雜，對于普通計算設備而言，極易造成內存溢出;同時也考慮到輸入的低分辨率圖像存在噪聲、模糊等情形. 為了解決這一問題，嘗試使用“分解”的策略進行解決. 針對每一個圖像片xi，在先驗給定的前提下，借助它的后驗概率密度函數進行計算，如式（19）所示：

式中：i是理想高分辨率圖像片xi的通過該算法得到的估計版本;‖yi - Di Hi x‖2與成本函數中的保真項‖Y-DHX‖2作用相同;（x - μXi）T∑-1Xi（x- μXi）與成本函數中的先驗項（Pi X - μXi）T∑-1Xi（Pi X - μXi）相一致;σ2與平衡參數λ相對應，但此時的σ2有著明確的意義，它表示輸入圖像中假定高斯白噪聲的方差. 通過對式（19）求導，并令導數為0，來求解此方程，可以得到每一個圖像片的表達式，最后，用估計到的圖像片集合{xi}N ?i=1，在忽略邊界位置處的影響后，根據式（20）構造完整的圖像X.

根據前述算法的描述，可以完成算法的一次迭代，通過判斷當前X和X′的差異是否足夠小，以決定算法是否需要執行下一次迭代. 當滿足輸出條件時，即可直接輸出X作為超分辨率重建的結果，這個超分辨率過程的偽代碼如圖3所示. 最后，在圖4中給出了本文算法對一幅彩色圖像進行超分辨率重建的完整過程.

3 ? 實驗結果與分析

通過主觀視覺觀察和客觀參數比較兩種方式驗證理想重建圖像自相似性先驗超分辨率算法的效率. 首先對算法流程中需要設定的參數進行說明，然后給出本文算法和同類以及前沿算法重建圖像質量、消耗時間的比較，最后對該算法的性能做進一步的理論分析.

3.1 ? 實驗設置

在實驗過程中，為了模擬成像過程，構建理想高分辨率圖像和低分辨率輸入圖像測試樣本對，用于測試算法的性能，我們在一些常用測試集中隨機抽取樣本作為理想的高分辨率目標，將這些抽取到的圖像用雙三次方法下采樣s倍，并用高斯低通濾波器（均值為0，方差為0.5）對它們濾波，以生成用于輸入的低分辨率圖像. 將這些低分辨率圖像輸入到測試算法中，超分辨率s倍，得到的重建結果和計算過程消耗的時間可用于評價該算法. 一般而言，圖像重建結果越接近理想目標圖像，計算過程消耗時間越少，算法的性能越高.

本文算法在首次迭代執行前，僅有輸入圖像Y已知，先將Y雙三次上采樣s倍的結果初始化為X′，再將X′使用雙三次下采樣s倍用于初始化Y′. 由于圖像尺度間的自相似性有隨著尺度的降低而減弱的特性，當超分倍數較大時，直接放大到目標倍數會降低重建圖像質量，為此我們采用逐級放大的方式進行處理，每次放大2倍，并將超分辨率結果作為算法的輸入再次放大，直到達到目標倍數為止，最后一次放大不足2倍時，直接放大到目標倍數. 對于輸入的彩色圖像，先將這幅圖像從RGB空間轉換到YUV空間，由于代表亮度信息的Y通道對人眼較為敏感，用本文提出的理想重建圖像自相似性超分辨率算法進行處理;代表顏色信息的U、V通道對人眼的刺激相對遲弱，U、V通道直接用雙三次上采樣方法放大到目標倍數，再將重建結果從YUV空間轉換到RGB空間進行顯示及保存.

另外，考慮到隨著算法迭代次數增加，重建結果中包含噪聲的能級應逐漸減少，將式（20）中描述噪聲等級的參數設定為σ = ，（T為算法的迭代次數）. 由于此算法考察的是圖像自相似性，不同尺度間的圖像片抽取尺寸相同，式（20）中圖像片尺寸參數設定為a = 7，即抽取尺寸為7 × 7的圖像片. 算法中的每一個未知超分辨率圖像片都需要在輸入圖像Y和它的低頻版本中對應的位置處設置窗口，以便抽取訓練樣本. 若窗口尺寸設置過大，則樣本間的一致性不強，影響模型的準確程度;若窗口尺寸設置過小，則會因為抽取到的樣本數量不足，導致模型欠擬合. 本文將窗口尺寸設定為w = 32，即每一個估計的圖像片都在輸入圖像與之相同中心位置 32 × 32的窗口中抽取訓練樣本. 對于邊界附近的超分辨率圖像片，為了能夠定位到相應的窗口，需要對圖像Y和Y′做鏡像擴展處理. 與窗口尺寸相匹配的高斯混合模型中高斯成分的個數設置為K = 3.

3.2 ? 主觀觀察結果

為了驗證本文算法的有效性，我們選擇與本文形式類似方法（包括Glasner[8]、GPR[16]、Self-ExSR[17]和MMPM[29]）、借助外界訓練集合方法（ScSR[2]、ASDS[31]、A+[4]、SPM[32]和JOR[33]）以及深度學習方法（SRCNN[5]、FSRCNN[6]、lapSRN[7]）進行了一系列的比對實驗. 所選擇的比較算法除Glasner算法外均從作者主頁下載，Glasner算法的代碼為我們使用Matlab2019b軟件自行編寫，且效果與文獻[8]中給出的結果基本一致. 本文算法和參與比較的算法均在Intel（R）Core（TM） i7-5600 CPU @ 2.60 GHz，8.00 GB緩存的硬件環境，Windows 7專業版64位操作系統，Matlab2019b的軟件環境下進行實驗.

如圖5和圖6所示，顯示的是圖像“parrot” 和“fence”使用多種不同方法分別放大3倍和4倍的結果. 觀察用線框標識出的局部子區域的放大顯示結果，可以發現在顯著邊緣位置、紋理細節豐富區域能夠明顯地保持邊緣和紋理的結構，能恢復出更多正確的細節，使圖像看上去更加清晰、自然. 兩組超分辨率結果中，ScSR、Glasner、Self-ExSR、GPR以及SPM方法重建的超分辨率圖像在顯著邊緣位置都出現了可見的模糊和噪聲. ASDS、A+、JOR、MMPM和本文提出的方法超分辨結果較為清晰，在顯著邊緣及紋理區域附近并未出現可見的噪聲和模糊等形式的偽影. MMPM方法和我們的方法恢復出了較多的高頻信息，觀察“parrot”圖像中鸚鵡的眼睛和羽毛區域以及“fence”圖像中帶有平行結構的“籬笆”，可以看出我們的方法對圖形結構保持得更加完整，幾乎觀察不到可見的變形.

圖7是方法和深度學習方法SRCNN和lapSRN對圖像“barbara”超分辨率放大4倍的比較結果. 測試圖像“barbara”包含豐富的紋理信息，在超分辨率過程中，這些紋理結構雖有固定的模式，卻又不盡相同，在超分辨率過程中極易產生變形或引入噪聲. 觀察圖7可以發現，我們的方法產生的超分辨率結果和理想高分辨率圖像最為接近，基本上保持住了紋理區域的外觀. SRCNN、lapSRN方法產生的超分辨率結果都使得紋理的基本結構發生了嚴重的變形，且能夠觀察到有明顯噪聲出現.

3.3 ? 客觀評價結果

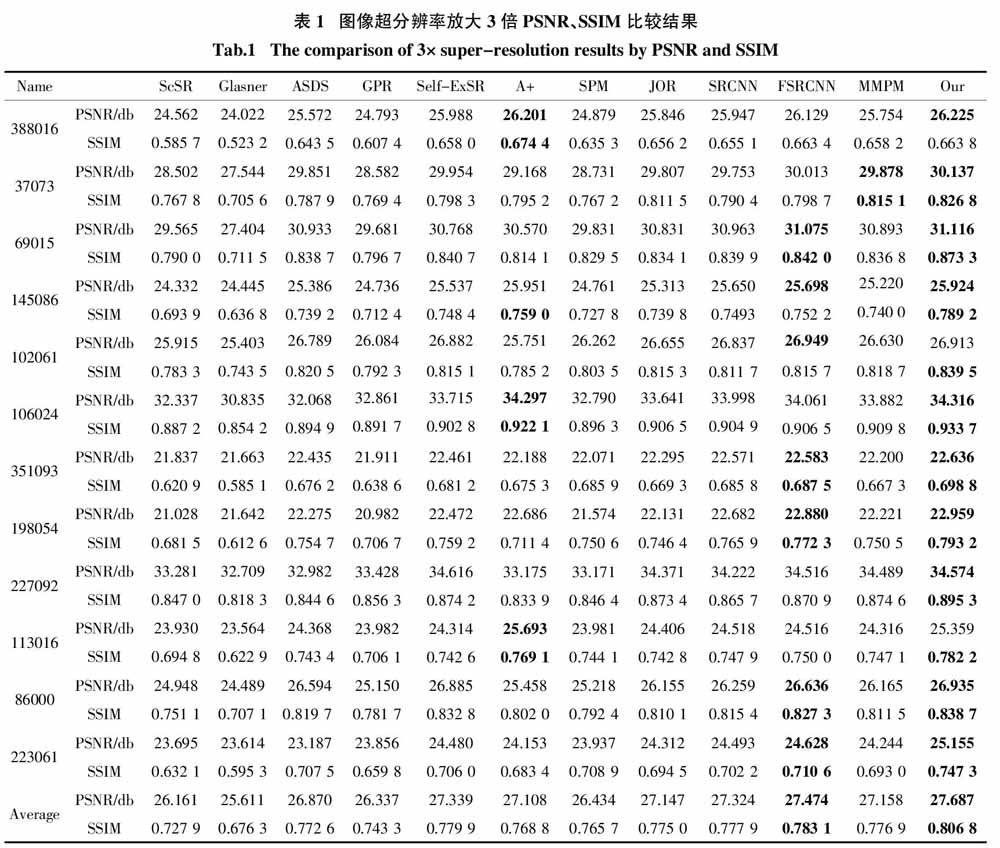
為了進一步說明理想圖像自相似性先驗超分辨率算法的性能，借助客觀評價參數對我們的方法和其他方法進行比較，主要使用的評價指標包括峰值信噪比（Peak Signal to Noise Ratio，PSNR）和結構相似性（Structural Similarity Index Measure，SSIM）. 一般來說，這兩個評價參數的數值越大，代表算法得到的重建圖像質量越好. 在BSD500圖像集合中隨機抽取12幅圖像，如圖8所示，這些圖像的內容囊括人物、動物、建筑物和風景等，包含顯著邊緣、復雜紋理和精細結構等內容，具有極強的代表性. 按照前述步驟操作，將這些圖像進行超分辨率放大3倍處理，其客觀參數比較結果如表1所示.

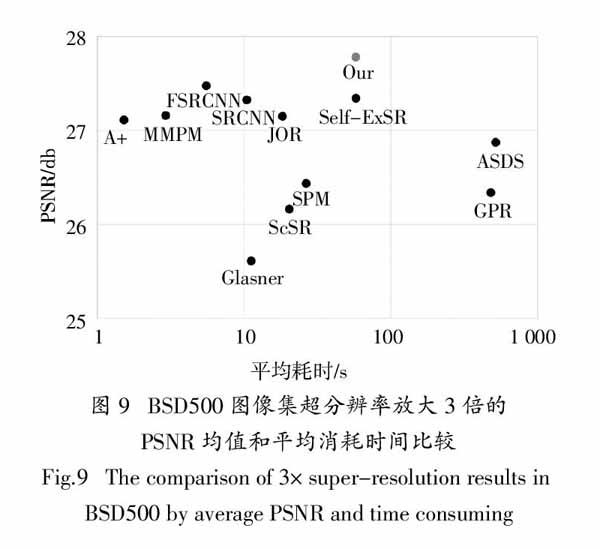
在表1中，每一行數據代表一幅圖像使用不同方法超分辨率的結果，每一列代表一種方法超分辨率處理不同圖像的結果，其中每一幅圖像對應兩行數據，第一行為PSNR結果，第二行為SSIM結果. 觀察表1可以發現，在PSNR參數比較中，表1中我們的方法有10張圖像結果最優;SSIM參數比較中，我們的方法有11張圖像結果最優（最優結果均用加粗字體標出）. 表1中我們的方法沒有得到最優結果的圖像，它們的評價參數數值也相對較大，都取得了次優結果. 另外，觀察表1中評價參數平均值，可以看出我們方法的PSNR和SSIM平均值都排在第1位，我們方法的PSNR平均值高于MMPM算法0.529 db，SSIM平均值高于MMPM算法0.030. 為了從統計的角度出發驗證本文算法的有效性，以BSD500圖像集合全體作為測試對象，用本文算法和參與比較的11種前沿算法分別對測試集中的圖像進行3倍放大. 其性能比較結果如圖9所示，圖中每一個實心圓點代表一個算法，每個點的橫坐標表示算法的平均消耗時間，縱坐標表示算法重建圖像的PSNR均值. 從圖9中可以看出，本文算法平均PSNR值最大，圖像質量最好. 該算法放大一幅BSD500中的圖像平均消耗時間約1 min，明顯少于GPR和ASDS算法，與Self-ExSR算法耗時相近.

3.4 ? 分析討論

首先，聯合高斯混合模型建模在形式上不同于訓練字典下的稀疏算法，它在解決超分辨率問題中有先天優勢. 因為超分辨率成像中的濾波矩陣和下采樣矩陣均為非單位矩陣，在與字典進行計算時，會導致訓練字典的互相干性增大[24]，降低重建圖像質量，而基于聯合高斯混合模型的超分辨率方法不存在這樣的問題.

在挖掘理想重建圖像自相似性的超分辨率算法中，對每一個待超分辨率的圖像片，該算法以當前圖像片的位置為中心構建窗口，僅使用少量的高斯成分對圖像片空間位置附近的樣本建模. 由于這些圖像片位置彼此相鄰，描述的內容相似，具有較強的一致性，能使訓練得到的高斯混合模型更加準確. 同理，Δik值也會體現出極強的稀疏性.

最后，已有方法都是將訓練得到的高斯混合模型作為先驗，并假定所有的圖像片都能由模型中后驗概率最高的高斯成分生成. 而我們的方法對這個高斯混合模型做進一步推導，把推導結論（每個未知的高分辨率圖像片都服從一個特定的高斯分布）作為先驗知識，設計成本函數. 二者的區別在于后者進一步挖掘了后驗概率最高的高斯成分，利用了這個高斯成分的協方差信息進行計算，使得圖像重建效果優于前者.

4 ? 總 ? 結

在超分辨率研究工作中，我們發現理想重建高分辨率圖像的自相似性體現最為強烈，而受降質因素影響的重建高分辨率圖像自相似性會明顯減弱.

當使用高斯混合模型對這一現象進行描述時，通過對模型進行推導，可以發現每一個理想的高分辨率圖像片的自相似性都符合一個特定的高斯分布. 將這個規律作為先驗知識添加到超分辨率框架中，顯著提升了重建超分辨率圖像的質量. 該方法無需使用外界圖像進行訓練，僅通過輸入圖像和其對應的低頻版本為每個重建圖像片建模，以一種在線訓練的方式聯合構建高斯混合模型. 隨著輸入圖像的變化，模型參數能夠自動進行調整，以適應新的情況. 因此該算法較其他預測模型有著更強的魯棒性，尤其適用于數字電視高清顯示等需要較大超分辨率倍數但又無額外參數存儲裝置的場景.

參考文獻

[1] ? ?NASROLLAHI K，MOESLUND T B. Super-resolution：a comprehensive survey[J]. Machine Vision and Applications，2014，25（6）：1423—1468.

[2] ? ?YANG J C，WRIGHT J，HUANG T S，et al. Image super-resolution as sparse representation of raw image patches[C]// Computer Vision and Pattern Recognition. Anchorage，AK：IEEE，2008：1—8.

[3] ? ?TIMOFTE R，DE SMET V，GOOL L V. Anchored neighborhood regression for fast example-based super-resolution[C]// 2013 IEEE International Conference on Computer Vision. Sydney：IEEE，2013：1920—1927.

[4] ? ?TIMOFTE R，DE SMET V，GOOL L V. A+：Adjusted anchored neighborhood regression for fast super-resolution[C]// Asian Conference on Computer Vision. Singapore：Springer，2014：111—126.

[5] ? ?DONG C，LOY C C，HE K M，et al. Image super-resolution using deep convolutional networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2016，38（2）：295—307.

[6] ? ?DONG C，LOY C C，TANG X O. Accelerating the super-resolution convolutional neural network[C]// European Conference on Computer Vision. Amsterdam：Springer，2016：391—407.

[7] ? ?LAI W S，HUANG J B，AHUJA N，et al. Fast and accurate image super-resolution with deep Laplacian pyramid networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2019，41（11）：2599—2613.

[8] ? ?GLASNER D，BAGON S，IRANi M. Super-resolution from a single image[C]// 2009 IEEE 12th International Conference on Computer Vision. Kyoto：IEEE，2009：349—356.

[9] ? ?ZONTAK M，IRANI M. Internal statistics of a single natural image [C]// Computer Vision and Pattern Recognition. Colorado：IEEE，2011：977—984.

[10] ?ZONTAK M，MOSSERI I，IRANI M. Separating signal from noise using patch recurrence across scales [C]// Computer Vision and Pattern Recognition. Portland，oregon，USA：IEEE，2013：1195—1202.

[11] ?MICHAELI T，IRANI M. Blind deblurring using internal patch recurrence [C]// European Conference on Computer Vision. Zurich：Springer，2014：1—16.

[12] ?LOTAN O，IRANI M. Needle-match：reliable patch matching under high uncertainty [C]// 2016 IEEE International Conference on Computer Vision and Pattern Recognition. Las Vegas：IEEE，2016：439—448.

[13] ?潘宗序，禹晶，胡少興，等. 基于多尺度結構自相似性的單幅圖像超分辨率算法[J]. 自動化學報，2014，40（4）：594—603.

PAN Z X，YU J，HU S X，et al. Single image super resolution based on multi-scale structural self-similarity [J]. Acta Automatica Sinica，2014，40（4）：594—603. （In Chinese）

[14] ?FREEDMAN G，FATTAL R. Image and video upscaling from local self-examples[J]. ACM Transactions on Graphics，2011，30（2）：1—11.

[15] ?YANG J C，LIN Z，COHEN S. Fast image super-resolution based on in-place example regression [C]// 2013 IEEE Conference on Computer Vision and Pattern Recognition. Portland，oregon，USA：IEEE，2013：1059—1066.

[16] ?HE H，SIU W C. Single image super-resolution using Gaussian process regression[C]// Computer Vision and Pattern Recognition. Colorado：IEEE，2011：449—456.

[17] ?HUANG J B，SINGH A，AHUJA N. Single image super-resolution from transformed self-exemplars[C]// 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston，MA：IEEE，2015：5197—5206.

[18] ?ZHA Z Y，YUAN X，ZHOU J T，et al. Image restoration via simultaneous nonlocal self-similarity priors[J]. IEEE Transactions on Image Processing，2020，29：8561—8576.

[19] ?LIN C H，BIOUCAS-DIAS J M. An explicit and scene-adapted definition of convex self-similarity prior with application to unsupervised sentinel-2 super-resolution[J]. IEEE Transactions on Geoscience and Remote Sensing，2020，58（5）：3352—3365.

[20] ?FAN L W，LI X M，FAN H，et al. Adaptive texture-preserving denoising method using gradient histogram and nonlocal self-similarity priors[J]. IEEE Transactions on Circuits and Systems for Video Technology，2019，29（11）：3222—3235.

[21] ?ZHA Z Y，ZHANG X G，WANG Q，et al. Group sparsity residual constraint for image denoising with external nonlocal self-similarity prior[J]. Neurocomputing，2018，275：2294—2306.

[22] ?ZHANG L，WEI W，SHI Q F，et al. Accurate imagery recovery using a multi-observation patch model[J]. Information Sciences，2019，501：724—741.

[23] ?肖進勝，單姍姍，易本順，等. 基于分區灰度投影穩像的運動目標檢測算法[J]. 湖南大學學報（自然科學版），2013，40（6）：96—102.

XIAO J S，SHAN S S，YI B S，et al. Moving targets detection based on subzone gray projection video stabilization[J]. Journal of Hunan University （Natural Sciences），2013，40（6）：96—102. （In Chinese）

[24] ?李明俊，張正豪，宋曉琳，等. 基于一種多分類半監學習算法的駕駛風格分類模型[J]. 湖南大學學報（自然科學版），2020，47（4）：10—15.

LI M J，ZHANG Z H，SONG X L，et al. Driving style classification model based on a multi-label semi-supervised learning algorithm[J]. Journal of Hunan University （Natural Sciences），2020，47（4）：10—15. （In Chinese）

[25] ?YU G S，SAPIRO G，MALLAT S. Solving inverse problems with piecewise linear estimators：from Gaussian mixture models to structured sparsity[J]. IEEE Transactions on Image Processing，2012，21（5）：2481—2499.

[26] ?ZORAN D，WEISS Y. From learning models of natural image patches to whole image restoration[C]//2011 International Conference on Computer Vision. Barcelona：IEEE，2011：479—486.

[27] ?NIKNEJAD M，RABBANI H，BABAIE-ZADEH M. Image restoration using Gaussian mixture models with spatially constrained patch clustering[J]. IEEE Transactions on Image Processing，2015，24（11）：3624—3636.

[28] ?SANDEEP P，JACOB T. Single image super-resolution using a joint GMM method[J]. IEEE Transactions on Image Processing，2016，25（9）：4233—4244.

[29] ?HUANG Y F，LI J，GAO X B，et al. Single image super-resolution via multiple mixture prior models[J]. IEEE Transactions on Image Processing，2018，27（12）：5904—5917.

[30] ?LU X，LIN Z，JIN H L，et al. Image-specific prior adaptation for denoising[J]. IEEE Transactions on Image Processing，2015，24（12）：5469—5478.

[31] ?DONG W S，ZHANG L，SHI G M，et al. Image deblurring and super-resolution by adaptive sparse domain selection and adaptive regularization[J]. IEEE Transactions on Image Processing，2011，20（7）：1838—1857.

[32] ?PELEG T，ELAD M. A statistical prediction model based on sparse representations for single image super-resolution[J]. IEEE Transactions on Image Processing，2014，23（6）：2569—2582.

[33] ?DAI D，TIMOFTE R，VAN GOOL L. Jointly optimized regressors for image super-resolution[J]. Computer Graphics Forum，2015，34（2）：95—104.

收稿日期：2020-12-17

基金項目：國家自然科學基金資助項目（61772144），National Natural Science Foundation of China（61772144）;廣東省自然科學基金資助項目（2017A030310618），Natural Science Foundation of Guangdong Province（2017A030310618）

作者簡介：李鍵紅（1981—），男，遼寧朝陽人，廣東外語外貿大學講師，碩士生導師，博士

通信聯系人，E-mail：wyrljh@163.com