基于LMD-IMVO-LSSVM的短期風速預測

桑茂景，謝麗蓉，李進衛，王 斌，3，楊 歡，4

（1.新疆大學 電力系統及發電設備控制和仿真國家重點實驗室風光儲分室，新疆 烏魯木齊 830047；2.中船重工海為（新疆）新能源有限公司，新疆 烏魯木齊 830002；3.山東鋼鐵集團日照有限公司，山東 日照276805；4.清華大學 電力系統及發電設備控制和仿真國家重點實驗室，北京 100084）

0 引言

隨著化石燃料的大量使用，化石能源枯竭及其所帶來的環境問題日益嚴峻。清潔、可持續的風能逐漸受到各國的高度重視。然而風能的間歇性、隨機性和不可控性，使得風電大規模并網存在巨大的挑戰，因此準確有效地預測風速對電力系統的平穩運行意義重大。

近年來，科研人員對風速預測已經做了大量的研究。目前，用于風速預測的方法主要有回歸分析方法、時間序列方法、馬爾科夫鏈方法、支持向量機方法和神經網絡方法等[1]～[5]。然而，在現實風速預測中，通過以上單一預測方法往往無法達到理想的預測效果，要對單一預測模型進行一定的優化和改進來提高風速的預測精度。文獻[6]采用了廣義回歸神經網絡的預測方法對風速進行預測，該方法具有結構簡單，方便實現，對訓練數據數量要求不高的特點，和BP神經網絡相比較，其預測的精確度和準確度有所提高；然后又對廣義回歸神經網絡中的光滑參數進行粒子群（PSO）優化選取，使其取值不再盲目，進一步提高了其預測精度。文獻[7]從4個方面對局部均值分解（LMD）和經驗模態分解（EMD）進行比較，結果表明，與EMD相比，LMD可以有效地消除模態混疊，從而獲得更準確的瞬時頻率。文獻[8]采用多元宇宙優化算法（MVO）對最小二乘支持向量機（LSSVM）模型的若干參數進行優化，取得了較高的建模精度。文獻[9]利用集合經驗模態分解法將風速序列分解為頻率不同的若干個分量，降低了風速序列的非平穩性；然后利用花朵授粉算法優化BP神經網絡構建預測模型，預測各個分量的變化趨勢；最后將各個分量的預測值進行疊加組合，得出最終的風速預測值。但是上述方法均未達到理想的預測效果。

鑒于LSSVM具有較強的泛化能力以及樣本問題處理能力等優點，本文采用改進多元宇宙算法（IMVO）對LSSVM參數進行尋優，并結合LMD方法，提出一種基于LMD-IMVO-LSSVM的風速預測模型。通過實驗仿真分析，所提方法有效提高了風速預測的精度。

1 局部均值分解

LMD是一種新的自適應非平穩信號的處理方法，可自適應地將一個復雜的多分量非平穩信號分解成若干個乘積函數（PF）之和[10]，其中每一個PF分量都是一個純調頻信號和一個包絡信號的乘積。在經典的LMD方法中，采用滑動平均法得到的局部均值函數和包絡估計函數會發生較明顯的相位偏移現象。為解決上述問題，本文采用三次樣條插值法進行平滑處理，LMD分解過程如下。

①找出原始信號x（t）的所有極值點并排序，分別對左、右端的極值點進行鏡像延拓[11]，從而得到 延 拓 后 的 序 列x＇（t）。

②對所有的極值點分別進行三次樣條插值，得到上包絡線Eup和下包絡線Edown。

③通 過 式（1）和 式（2）求 出 局 部 均 值 函 數m11（t）和 包 絡 估 計 函 數a11（t）。

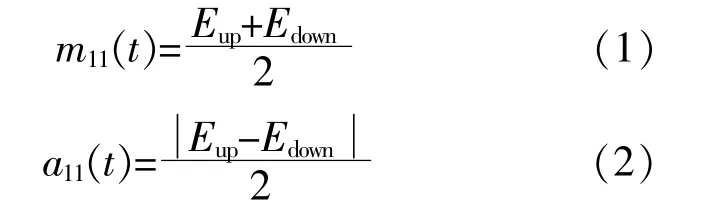
④將m11（t）從 原 始 信 號x＇（t）中 分 離 出 來，得到 剩 余 量h11（t），對h11（t）進 行 解 調，得 到 調 頻 信號s11（t）。

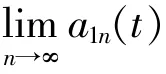
⑥將上述過程中產生的所有包絡估計函數相乘，得 到 包 絡 信 號a1（t）。將a1（t）和s1n（t）相 乘，得到 信 號x＇（t）的 第 一 個PF分 量。

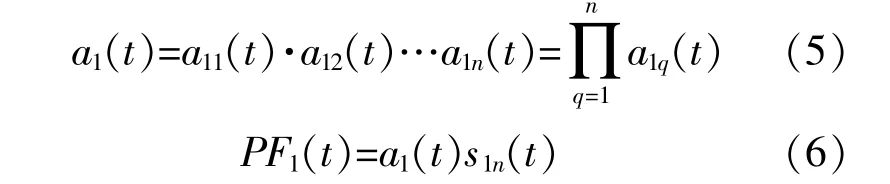
PF1（t）的 瞬 時 頻 率f1（t）可 由s1n（t）求 出:

⑦將PF1（t）從 原 始 信 號x＇（t）中 分 離 出 來，得到 一 個 新 信 號u1（t）。對u1（t）重 復 上 述 步 驟k次，直到uk（t）為常數或一個單調函數為止。

至此，將原始信號分解為k個PF分量和一個剩余分量uk之和。

2 基于LMD-IMVO-LSSVM的風速預測模型

2.1 LSSVM及核函數選擇

LSSVM是對支持向量機（SVM）的一種改進，將QP問題轉化為求解線性方程組問題，將不等式約束變為等式約束，從而方便了Lagrange乘子alpha的求解，提高了收斂速度[12]。對于給定訓練集:

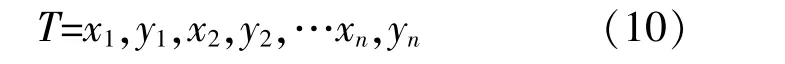
假設其回歸函數為

式中:x為樣本輸入；y為樣本輸出；ω和b分別為高維空間中超平面的法向量和截距。

根據風險最小化原則，回歸問題可以轉化為約束問題。

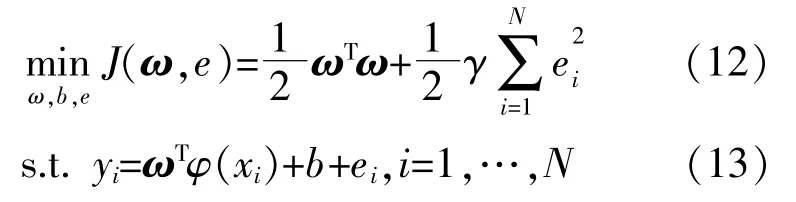
式中:ei為松弛變量；γ為正則化因數。

引入Lagrange乘子α，上述問題轉化為

分 別 對 ω，b，e，α求 偏 微 分，得 到 最 優 值，進而建立回歸函數:

式 中:K（x，xi）為 核 函 數。

在用LSSVM進行風速預測時，核函數類型對LSSVM回歸性能有很大的影響。LSSVM常用的核函數有線性核函數、徑向基核函數、多項式核函數和傅里葉核函數等。文獻[13]通過對不同核函數的仿真分析，得出徑向基核函數的預測精度較高，因此本文選用徑向基核函數，其表達式為

式中:σ為核寬度。

懲罰因子 γ和 σ是影響LSSVM預測性能的主要參數，為提高模型的預測精度，本文采用改進多元宇宙算法尋優這兩個參數，來提高風速預測精度。

2.2 MVO

MVO是Seyedali Mirjalili受到多元宇宙理論的啟發提出來的元啟發式優化算法[14]。主要根據多元宇宙理論的3個主要概念-白洞、黑洞和蟲洞，來建立數學模型。

MVO算法中的可行解對應宇宙，解的適應度對應該宇宙的膨脹率，在每一次迭代中，根據膨脹率對宇宙進行排序，通過輪盤賭隨機選定一個宇宙作為白洞，宇宙間通過黑、白洞進行物質交換。假定:

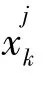
宇宙之間通過蟲洞隨機傳送物質以保證種群多樣性，同時都與最優宇宙交換物質以提高膨脹率。

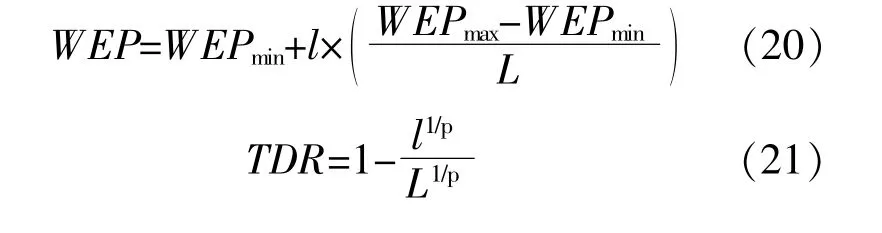
WEP和TDR均為MVO的重要參數。式中:WEPmax和WEPmin分別為參數WEP的上、下界，取0.2和1；l和L分別為當前迭代次數和最大迭代次數；p為算法的開發精度，取6。

MVO算法的優化進程始于種群的隨機初始化，通過多個宇宙的并行迭代搜索，最終得到問題的近似最優解。

2.3 IMVO

MVO算法主要依靠蟲洞進行穿越尋優，在最優宇宙附近進行旅行，TDR是影響算法性能的重要參數，但MVO中的TDR變化幅度較為單一，不能同時滿足精確與高效的要求。由MVO的定義可知，TDR值較大時可提高全局探索能力，TDR值較小時可增強局部深度開發，因此，為實現在迭代前期保持較快的迭代趨勢進行全局探索，迭代后期保持較慢的迭代趨勢進行局部開發的要求，本文提出新的旅行距離率TDR。

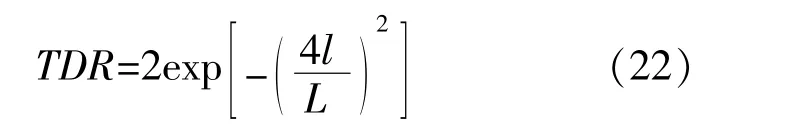
同時，為了更有效地找出所優化參數的最大范圍，對全局變量更新機制進行改進，當l＞L/2時，開始使用新的變量更新機制。

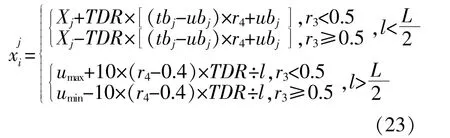
改進的變量更新方法有兩個主要特點:一是只在當前最優解的最大值和最小值附近搜索；二是新機制下，變量更新不再依賴宇宙邊界tbj和ubj。這使得在處理包含大量數據的預測問題時，算法優化更快，更加突出對參數的搜索。

IMVO算法運行流程如下:

①定 義各參數，包括宇 宙維 度d，n，WEP，L，tbj和ubj等；

②初始化多元宇宙種群U；

③根據式（19）執行輪盤賭機制；

④計算各宇宙的膨脹率，確定當前最優宇宙；

⑤根 據 式（20），（22）更 新WEP和TDR；

⑥根據式（23）更新最優宇宙，優于當前最優宇宙時將其替換，反之則保留當前最優宇宙；

⑦判斷是否最大迭代次數，是，終止循環，輸出最優宇宙和目標函數值；反之，則迭代次數加1，跳轉至③繼續循環。

IMVO算法流程如圖1所示。

圖1 IMVO算法流程圖Fig.1 Flow chart of IMVO algorithm

2.4 基于LMD-IMVO-LSSVM的風速預測方法

風速時間序列具有非線性、隨機性和不穩定性，直接對風速時間序列進行預測難以獲得精準的預測結果。

本文利用LMD對風速信號進行分解，采用IMVO優化LSSVM模型的2個參數，從而建立了LMD-IMVO-LSSVM的風速預測模型，具體方法如下:

①對數據整理分析并歸一化處理，得到原始風速序列；

②對原始風速序列進行LMD分解，得到從高頻到低頻的一系列PF分量和uk；

③對分解得到的每個分量，分別建立IMVOLSSVM模型，以每個子序列的平均絕對誤差作為目標函數值，采用改進多元宇宙算法優化γ和σ這兩個參數，并進行風速預測；

④疊加不同頻率下的風速預測序列，形成最終的風速預測值；

⑤誤差分析。

LMD-IMVO-LSSVM的預測流程如圖2所示。

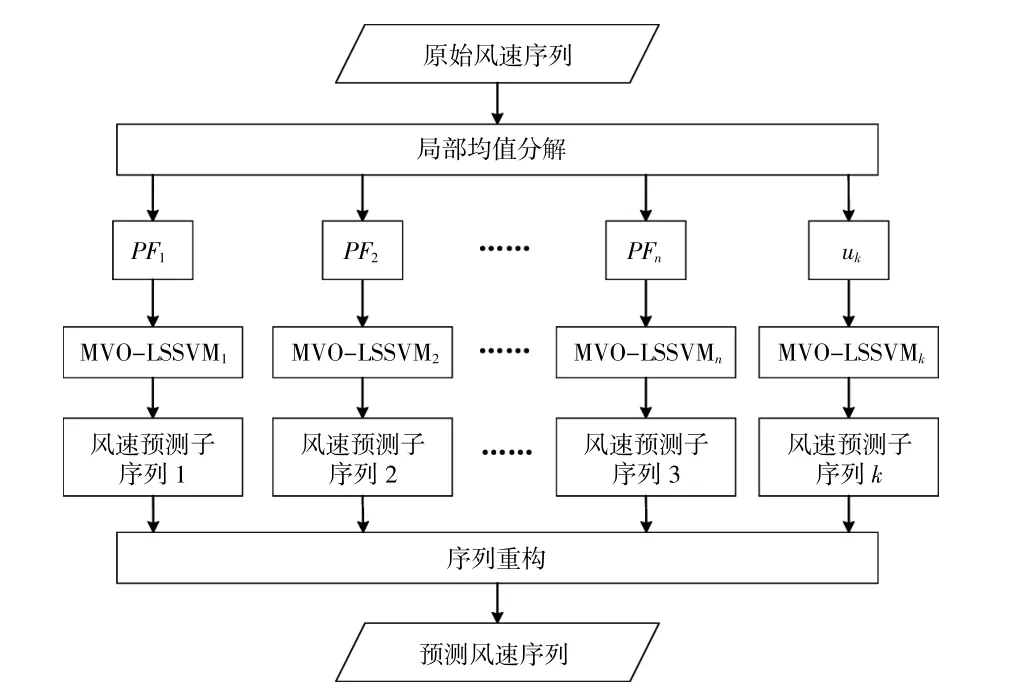
圖2 基于LMD-IMVO-LSSVM的風速預測流程圖Fig.2 Flow chart of wind speed prediction based on LMD-IMVO-LSSVM

3 算例分析

3.1 算例說明

本文原始數據選自新疆某風電場的實測數據，采樣間隔為15 min，共采取了600個樣本點，采取的風速時間序列曲線如圖3所示。取前500個樣本點作為訓練集，后100個樣本點作為測試集。

圖3 新疆某風電場風速實測曲線Fig.3 Wind speed measurement curve of a wind farm in Xinjiang

根據《NB/T31046-2013風電功率預測系統功能規范》，本文選取均方根誤差（RMSE）和平均絕對誤差（MAE）作為預測結果的評價指標。

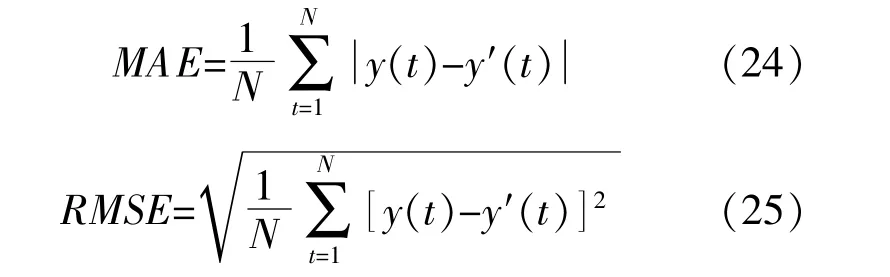
式 中:N為 采 樣 點 數；y（t）為t時 刻 的 預 測 值；y＇（t）為t時刻的實際值。

3.2 LMD分解結果

對采集的600個風速樣本點進行LMD分解，分解得到4個PF分量和一個uk，分解曲線如圖4所示。

圖4 LMD分解曲線Fig.4 LMD decomposition curve

由圖4可知:uk主要反映了風速曲線的基頻擾動，其變化規律與圖3的變化規律基本一致；PF4主要反映uk上的局部擾動，體現了局部風速的變化規律；PF2及PF3分量反映出風速序列中包含的低頻、高頻均值為零的隨機風速信息，其幅值波動大小反映瞬時風速變化程度；PF1分量反映平均風速信息，其風速約為10 m/s。

3.3 預測結果分析

采用IMVO算法優化預測模型中精度受到影響的2個參數，設置 γ和 σ的尋優范圍為（0.1，1 000），將分解后每個子序列訓練的MAE作為優化目標函數，IMVO算法優化模型參數的值如表1所示。

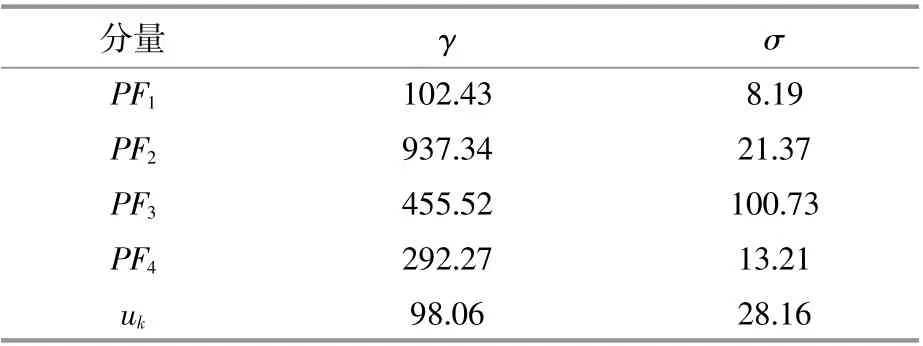
表1 IMVO的參數尋優結果Table 1 The parameter optimization results of IMVO

原始風速時間序列經過LMD分解得到了4個PF分量和1個剩余分量，采用改進的MVO算法對LSSVM參數進行尋優，最終建立了一種LMD-IMVO-LSSVM的風速預測模型。為驗證所提模型的預測精度，本文還分別對LSSVM模型、LMD-LSSVM模型、LMD-PSO-LSSVM模型和LMD-MVO-LSSVM模型進行風速預測，預測結果如圖5所示。

圖5 風速預測結果Fig.5 Wind speed prediction results

由圖5可知:利用LSSVM直接進行預測時，對于風速波動不敏感，且誤差相對較大；LMD方法分解出多種頻率的風速信息，能增加預測的準確性，但未經算法優化的LMD-LSSVM只能大致符合風速序列的基頻波動，在面對短時風速波動時仍然存在較大的誤差；經過LMD方法分解后，由PSO，MVO和IMVO 3種優化算法對LSSVM核函數優化后的LSSVM不僅能有效地預測出風速序列的基頻波動，其局部波動也能被準確地預測，能夠有效對原始的風速曲線進行擬合。

對本文所建立的5種預測模型進行誤差分析，誤差指標如表2所示。

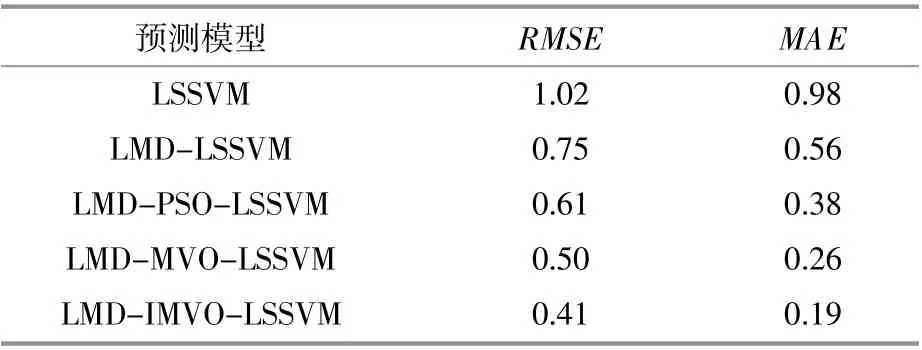
表2 5種模型誤差評價指標Table 2 5 model error evaluation indexes

由表2可知，IMVO優化的LSSVM模型RMSE誤差為0.41，MAE誤差為0.19，在5種模型中誤差指標最小。該結果驗證了IMVO算法具有較好的尋優能力，適用于徑向基核函數的尋優過程。

4 結論

本文利用IMVO算法對LSSVM參數進行尋優，結合LMD數據分解方法，提出了一種基于LMD-IMVO-LSSVM的風速預測模型。通過仿真實驗對比分析，得出以下結論。

①針對風速時間序列具有隨機性的特點，利用LMD提取出的不同特征信息進行預測，消除了模態混疊現象，可有效提高預測精度。

②尋優結果表明，IMVO算法的全局尋優能力優于MVO和PSO算法。

③利用IMVO算法對LSSVM參數進行尋優，通過對比分析，發現本文提出的LMD-IMVOLSSVM預測模型的預測精度更高，預測結果也更加貼合實際數據。