謹防靜摩擦因數(shù)足夠大的一個“陷阱”

鄭 金

(凌源市職教中心 遼寧 朝陽 122500)

對于兩個固體的接觸面，動摩擦因數(shù)是有限值，當相互作用的彈力很小時，摩擦力不可能很大；當相互作用的彈力為零時，不可能存在摩擦力.但在某些力學(xué)競賽題中給出“靜摩擦因數(shù)足夠大”的條件，由此默認為靜摩擦力足夠大，而且物體始終不滑動[1].這種觀點是不正確的，下面對一道錯題及其解答進行探討.

1 原題與錯解

【原題】在水平地面上，豎直直立一根長為2a,質(zhì)量為m的勻質(zhì)直桿，桿與地面間的靜摩擦因數(shù)足夠大.現(xiàn)對桿施一微擾，使其從豎直位置開始自由倒下，如圖1所示，求：當桿與豎直方向的夾角為多大時，桿的下端開始脫離地面？

圖1 傾倒的直桿

原解：從初始狀態(tài)到桿恰好離地瞬間，由機械能守恒定律有

(1)

其中直桿繞端點轉(zhuǎn)動時的轉(zhuǎn)動慣量為

(2)

以直桿與地面接觸點為軸，由轉(zhuǎn)動定理有

mgasinθ=Iβ

(3)

由式(1)、(2)可得直桿的角速度平方為

(4)

由式(2)、(3)可得桿轉(zhuǎn)動的角加速度為

(5)

直桿質(zhì)心繞接觸點轉(zhuǎn)動的切向加速度和法向加速度分別為

(6)

(7)

剛好離開地面的瞬間，桿在豎直方向只受重力作用，由牛頓第二定律有

mg=matsinθ+mancosθ

(8)

可得直桿與豎直方向的夾角為

2 探討與修正

上述解法看似正確，但所得結(jié)果卻是錯誤的.因為在推導(dǎo)過程中，默認為桿始終不滑動，而實際上，當θ=70.53°時，桿早已發(fā)生滑動，因此原題有缺陷.為了修正錯題和錯解，下面對原題進行拓展與解答.

解析：(1)對桿在水平方向和豎直方向分別由質(zhì)心運動定理有

f=matcosθ-mansinθ

mg-N=matsinθ+mancosθ

可得桿受到地面的靜摩擦力與彈力分別為

隨著偏轉(zhuǎn)角θ從零開始增大，cosθ從最大值1開始逐漸減小，可知地面彈力N單調(diào)遞減，最大值等于mg,最小值為零.假設(shè)桿的下端始終不動，當剛好離開地面時，受到彈力為零，即

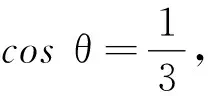
剛開始，由于直桿沒有相對滑動趨勢，因此摩擦力為零，隨著偏轉(zhuǎn)角的逐漸增大，摩擦力再次為零，由此可知，在兩個零之間存在最大值，則靜摩擦力先增大，再減小到零.當靜摩擦力減小到零時，桿對地面的壓力大于零，因此不是分離狀態(tài)，而是摩擦力改變方向的臨界狀態(tài).在臨界狀態(tài)之前，桿受到地面的摩擦力方向向右，在臨界狀態(tài)之后，桿受到摩擦力的方向向左，然后逐漸增大.

下面求向右的靜摩擦力取最大值時桿的偏轉(zhuǎn)角.

先把靜摩擦力的關(guān)系式去括號，再取導(dǎo)數(shù)為

令f′=0，可得關(guān)于cosθ的一元二次方程

6cos2θ-2cosθ-3=0

解方程得

可知桿的偏轉(zhuǎn)角略小于30°，且fmax≈0.2mg.

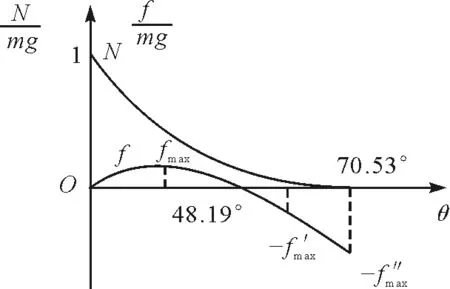
圖2 彈力和摩擦力隨偏轉(zhuǎn)角變化的圖像

(2)由于靜摩擦因數(shù)足夠大，因此在靜摩擦力減小到零之前，桿沒有發(fā)生滑動，則由

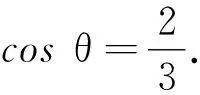
可知當摩擦力減小為零時桿的偏轉(zhuǎn)角為θ=48.19°.

此時桿受到地面的彈力大小為

(3)當桿的偏轉(zhuǎn)角小于48.19°時，桿沒有發(fā)生滑動，那么當桿的偏轉(zhuǎn)角大于48.19°時，由于壓力逐漸減小，桿將發(fā)生滑動，考慮到摩擦力小于零，可知當桿剛好發(fā)生滑動時，滿足-f=μN，即

化簡得

3sinθ(2-3cosθ)=μ(3cosθ-1)2

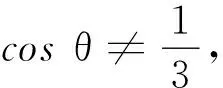
θ≠70.53°

如圖2所示，當桿與豎直方向的夾角大于48.19°時，隨著正壓力的減小，當反向摩擦力達到某一數(shù)值-f′max時，桿將發(fā)生滑動.在假設(shè)桿始終不滑動的條件下，當桿剛要離開地面時，與豎直方向的夾角為θ=70.53°，此時正壓力趨于零，靜摩擦力達到另一個最大值-f″max，但這是不可能實現(xiàn)的，因為在偏轉(zhuǎn)角達到70.53°之前，桿早已發(fā)生滑動了，因此當桿剛要離開地面時，與豎直方向的夾角不等于70.53°.

秀容月明告退，一直低眉順眼站在旁邊的內(nèi)侍走了過來，皇上，秀容月明這只老虎好不容易被關(guān)進籠子里，現(xiàn)在你放他出來，就怕放虎容易捉虎難啊！

假設(shè)把原題作為競賽題，那么對于“靜摩擦因數(shù)足夠大”的條件，參賽者將如何理解呢？如果認為桿始終不會滑動，雖然不切合實際，但卻可以順利解題；如果認為桿將會發(fā)生滑動，雖然合乎實際，但卻難以解題，那么只能跳入題中默認的“陷阱”，即認為：只要靜摩擦因數(shù)足夠大，當正壓力不為零時，靜摩擦力就足夠大；或者說，只要靜摩擦因數(shù)足夠大，物體就始終不發(fā)生滑動.這種觀點顯然是錯誤的，但卻有一定的迷惑性，因此很容易誘發(fā)錯題與錯解的出現(xiàn).

綜上可見，原題的設(shè)問與條件不自洽，需進行修正，有多種修改方法，既可改變條件，如把原題中的“桿與地面間的靜摩擦因數(shù)足夠大”替換為“桿下端放入淺槽內(nèi)不能滑動”；也可改變設(shè)問，把原題中的1個設(shè)問替換為新拓展的3個設(shè)問.此外，桿的長度2a可改為2b，以免在解題時用到的字母與加速度符號雷同.

3 總結(jié)與啟示

通過對原題進行修正或改編，可形成若干優(yōu)質(zhì)試題，具有一定的教學(xué)價值，既可作為大學(xué)物理復(fù)習(xí)資料，也可用于高中物理競賽訓(xùn)練.

雖然原題及其解答的錯誤起因于“靜摩擦因數(shù)足夠大”，但這個條件本身沒有錯，從修改原題設(shè)問的角度而言，在原題中給出這個條件是必要的，以此表明在靜摩擦力從最大值減小為零之前，桿不會發(fā)生滑動，為試題的改編與解答準備了條件.但若根據(jù)這個條件默認為桿始終不發(fā)生滑動則是錯誤的，或者說，對于如何保證桿始終不發(fā)生滑動，題中所設(shè)定的條件不合乎實際，由此導(dǎo)致試題的設(shè)問與條件不自洽.

因此在編擬試題時，不僅要體現(xiàn)試題的基礎(chǔ)性、綜合性、應(yīng)用性和創(chuàng)新性，更要遵循科學(xué)性與自洽性的原則，這就需要在編題過程中對試題的背景、情境、賦值、條件和設(shè)問等方面進行反復(fù)推敲和嚴格論證，確保其規(guī)范合理，嚴謹周密，不存在科學(xué)性錯誤.

在教學(xué)或者教研過程中，無論選題或答題都需謹慎，以免出現(xiàn)錯題或錯解.還要提倡學(xué)術(shù)爭鳴，敢于質(zhì)疑，善于發(fā)現(xiàn)并且及時糾正錯誤，對于那些比較隱蔽的、或者是勉強默認的、甚至是廣為流傳的錯誤，有必要進行深入剖析，以正本清源.若能充分利用錯題資源，變廢為寶，將有助于對相關(guān)知識的確切理解和正確應(yīng)用，更有利于提升學(xué)科核心素養(yǎng).