非線性汽流激振力對超超臨界汽輪機轉子運動特性的影響

曹麗華， 顏 洪， 司和勇

(東北電力大學 能源與動力工程學院，吉林 吉林 132012)

隨著機組參數的升高，汽流激振問題逐漸突出，成為限制機組出力、影響機組安全的一個主要原因。

1940年美國GE公司首次在試驗中發現了汽流激振現象，便對汽流激振展開研究。在理論研究方面，國外學者先后建立單控制體模型、雙控制體模型、三控制體模型、流線型模型等。其中Alford[1]的間隙激振力的計算公式和Muszynska流體激振力模型具有較廣泛的應用，但存在著系數選擇困難和需要線性化處理等局限。隨后又有學者對汽流激振的機理進行研究。Chen等[2]指出汽流激振包括葉頂間隙汽流激振，汽封汽流激振和不對稱蒸汽汽流激振。Cao等[3]分析了偏心條件下泄漏流動的不穩定性和壓力波動，得出圍帶表面泄漏渦引起的壓力波動是引起蒸汽激振力的主要因素。Li等[4]根據突變理論、非線性振動理論以及流體動力學，對汽輪機調節級在部分進汽下導致的汽流激振突變性能進行了定量分析。

隨著計算流體動力學(computational fluid dynamics,CFD)技術的發展，越來越多的學者開始使用這一方法進行汽流激振的研究。李彬等[5]應用商用軟件ANSYS-CFX數值模擬了汽流激振對汽輪機末級長葉片的影響。屈煥成等[6]對汽輪機調節級進行了三維全周數值模擬，分析了汽流激振力的頻率分布。Li等[7]利用計算流體力學CFD的結果，得到了Muszynska模型氣體激振力的經驗參數，研究了迷宮密封轉子系統在燃氣激振力作用下的1∶2次諧波共振。Huang[8]通過模擬含動葉頂間隙和轉子振動的復雜流場，建立了一種新的蒸汽力非線性模型。諶莉[9]對某1 000 MW機組的高壓缸的軸封和調節級進行了三維數值模擬，得到不同偏心和渦動狀態下的汽流激振力分布情況。

在汽流激振力研究的基礎上，一些學者開展了汽流激振對轉子系統的影響研究。Kim等[10]通過流固耦合對轉子系統的穩定性進行了分析。甕雷等[11]利用葉片汽流激振力分析了裂紋轉子系統的運動特性。劉思涌等[12]采用非線性Galerkin 法求解控制方程和運動方程，得到密封力對系統的影響。張恩杰等[13]利用雙控體模型確定密封腔內的軸向流速從而得到Muszynska密封力模型中的相關參數，并研究了密封力對轉子系統的影響。楊懿等[14]研究汽輪機組兩端軸封的汽封力對轉子振動與穩定性的影響。Zhang等[15]應用能量法建立了轉子-軸承-基礎迷宮密封系統的動力學模型，數值研究幾何參數和工作條件對轉子系統非線性動力學行為的影響。Li等[16]基于突變理論、非線性振動理論和流體力學提出了蒸汽激振力作用下調節級的非線性動力學模型。谷偉偉等[17]計算了含汽流激振的復雜激勵下的葉片系統的非線性振動響應。

當前汽流激振對轉子系統非線性運動的影響研究主要是采用理論公式。但這種模型存在非線性強度不夠、僅適用于小擾動和小偏心的局限性。此外，大部分關于轉子非線性運動研究中的轉子模型參數并不是實際機組的，導致計算結果脫離實際。基于以上問題，本文利用CFD建立1 000 MW超超臨界汽輪機的高壓缸1.5級三維全周模型，通過動網格技術和多頻渦動模型得到較為準確的非線性汽流激振力。并建立實際機組參數的轉子-軸承-密封系統，利用Runge-Kutta法求解微分方程組，通過最大Lyapunov指數分析非線性汽流激振力對轉子系統穩定性的影響。

1 轉子-軸承-密封系統數學模型

基于Jeffcott轉子模型，本文考慮油膜軸承的作用，模化超超臨界汽輪機高壓轉子，研究非線性汽流激振力對圓盤運動的影響，建立如圖1所示的對稱剛性油膜支承的轉子-軸承-密封系統。研究中忽略扭轉振動和陀螺力矩，只考慮轉子的橫向振動。圖1中:O1、O2分別為軸承和圓盤幾何中心，O3為轉子質心；轉子兩端由半徑為R、長為L的滑動軸承支承;m1、c1和m2、c2分別為軸承和圓盤的等效集中質量和結構阻尼;e為圓盤的質量偏心距;fx、fy分別為軸承x、y方向的非線性油膜力;Fax、Fay分別為數值模擬得到的1.5級密封所產生的x、y方向的非線性汽流激振力。圓盤與軸承之間為無質量彈性軸。

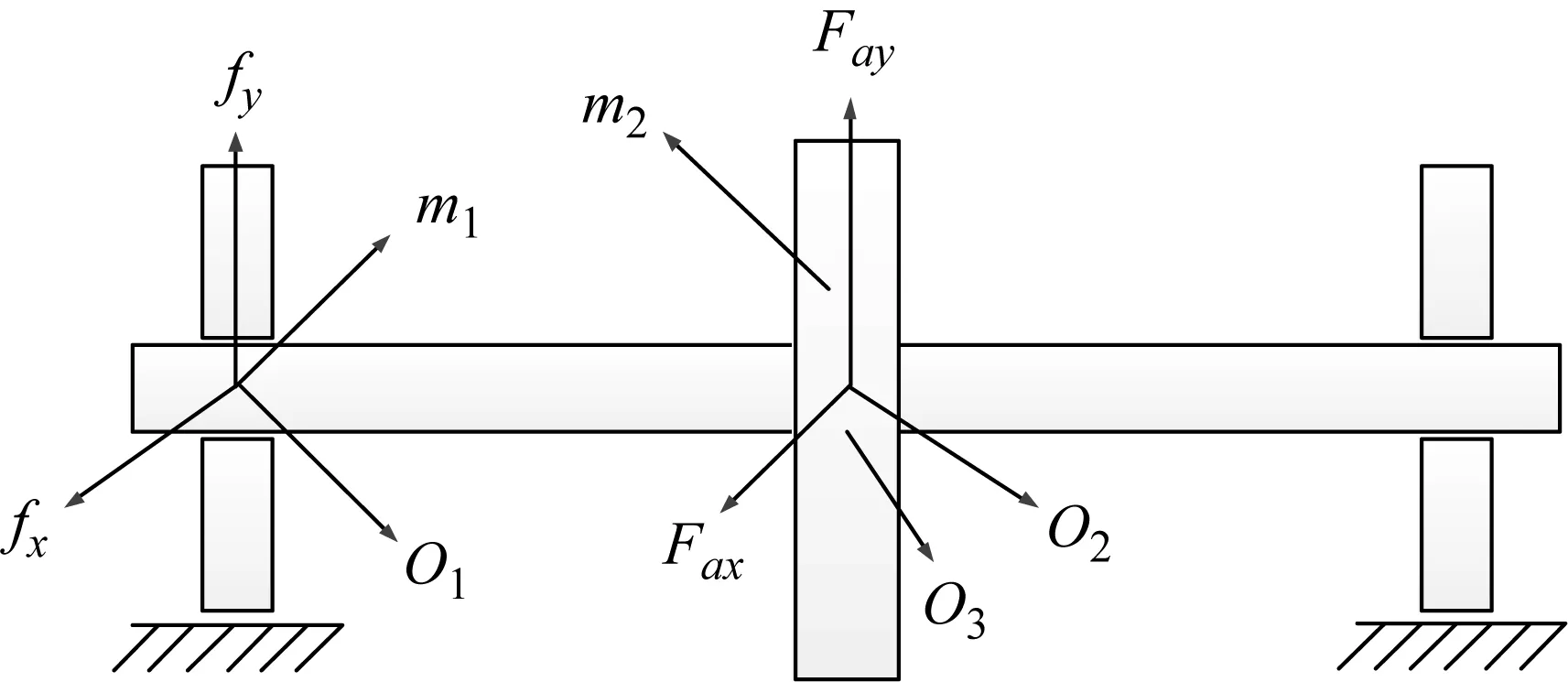
圖1 轉子-軸承-密封系統示意圖Fig.1 Schematic diagram of rotor bearing seal system

1.1 非線性汽流激振力模型

以某1 000 MW超超臨界汽輪機高壓缸第二級動靜葉柵，建立帶有密封的1.5級物理模型以研究所產生的非線性汽流激振力，二維截面模型如圖2所示。葉頂圍帶和靜葉環密封的二維截面模型如圖3所示，結構參數如表1所示。

圖2 1.5級示意圖Fig.2 Level 1.5 schematic diagram

表1 葉頂圍帶和靜葉環密封結構參數Tab.1 Structural parameters of blade topshroud and stator ring seal

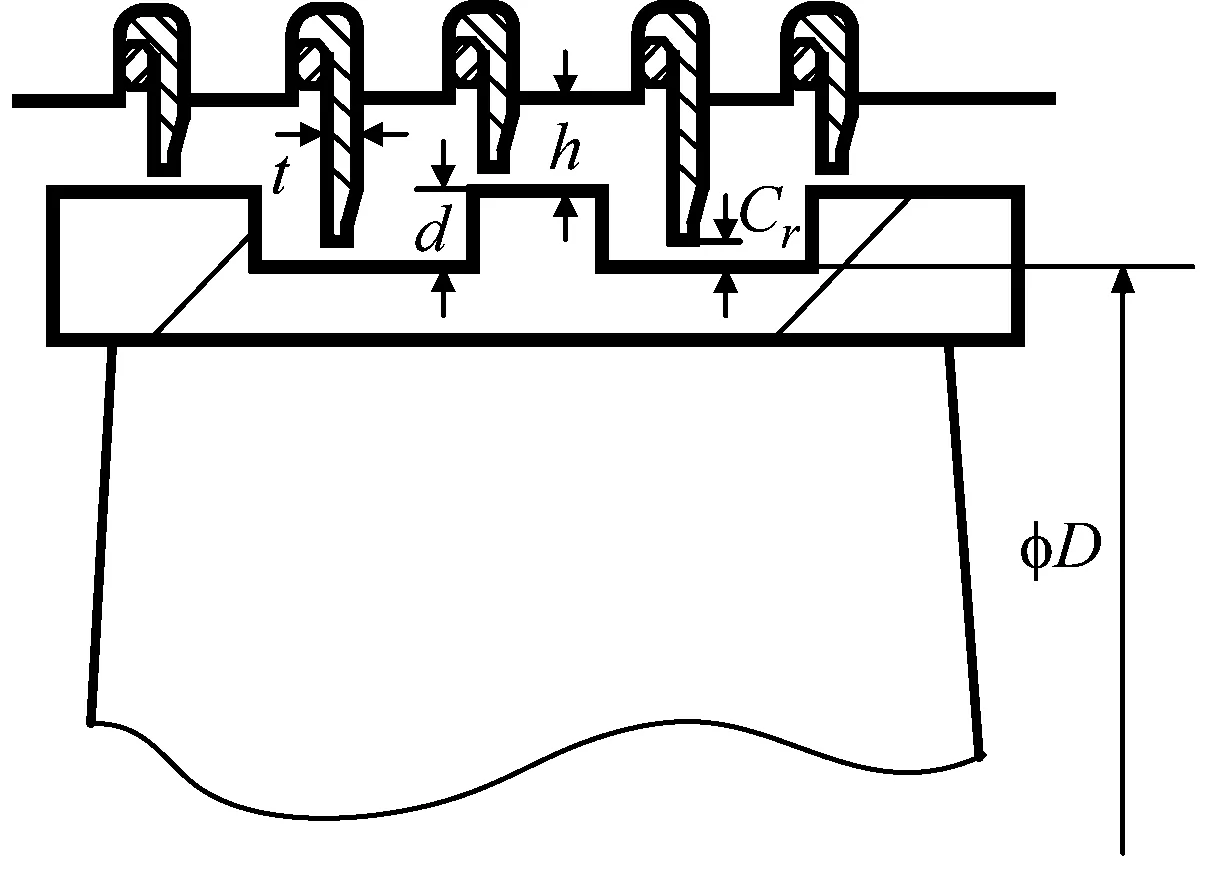
(a) 葉頂圍帶示意圖

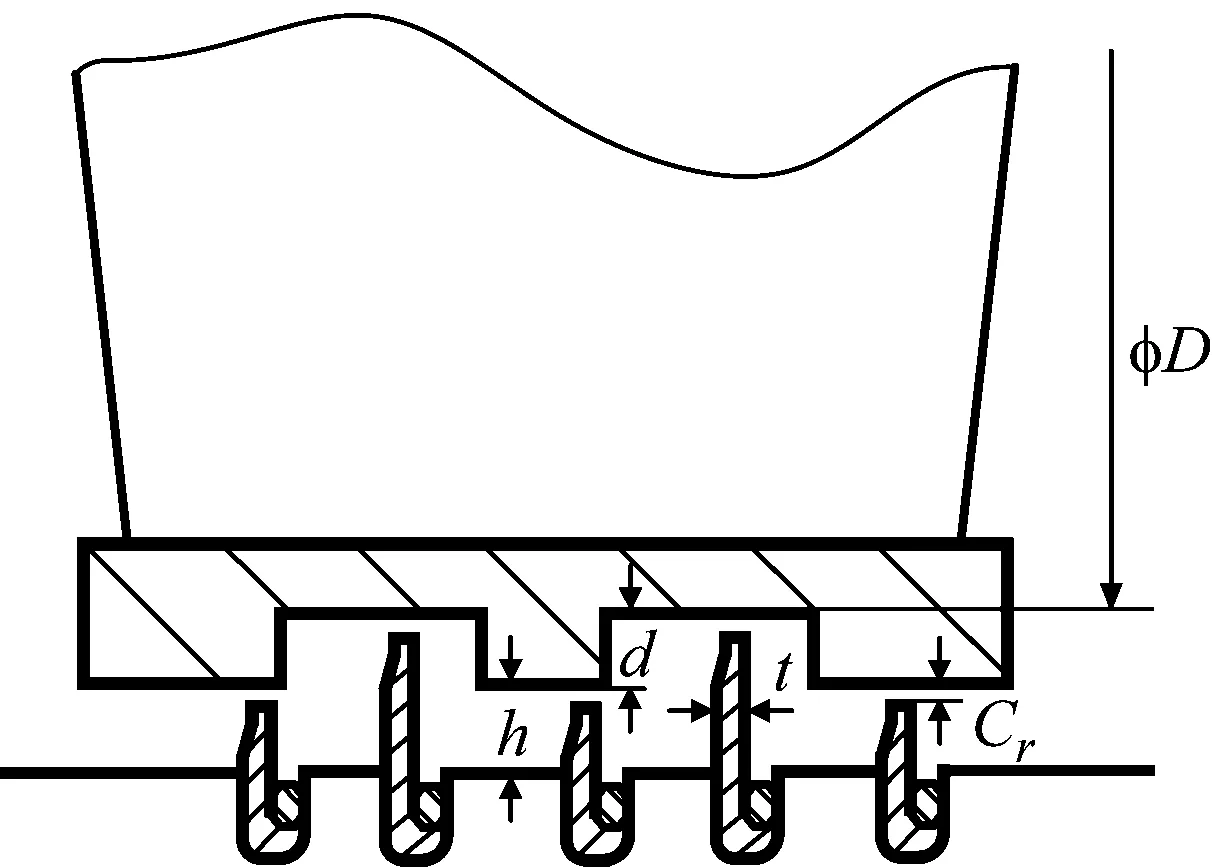
(b) 靜葉環密封示意圖圖3 葉頂圍帶和靜葉環密封示意圖Fig.3 Sealing diagram of blade top shroud and stationary blade ring

根據1.5級的實際幾何結構參數，建立三維全周模型如圖4所示。利用CFD/Fluent計算隨負荷變化的非線性汽流激振力。由于實際的轉子渦動是動偏心的，故網格域是隨著渦動變化的，于是采用動網格技術。

圖4 1.5級模型Fig.4 Level 1.5 model

圓盤渦動采用多頻渦動模型[18-19]，渦動方程表達式如下

(1)

(2)

邊界條件參數采用汽輪機各負荷下的蒸汽參數。額定工況下設定計算模型的工作條件如表2所示。計算方法的準確性在相關研究中被證明[20-22]。根據機組不同THA工況下的運行參數可得到不同負荷下的非線性汽流激振力。

表2 額定工況的工作條件Tab.2 Working conditions of rated working condition

利用用戶自定義函數(user defined function,UDF)設定轉子多頻渦動軌跡，得到不同偏心量和渦動頻率的非線性汽流激振力，如圖5所示。

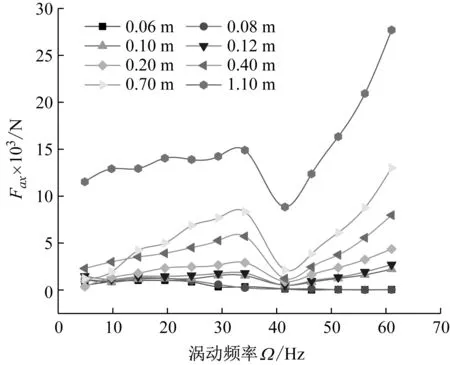
圖5 不同偏心量下的激振力Fig.5 Excitation force under different eccentricities

通過MATLAB擬合得到多項式表示的非線性汽流激振力函數如下

Fax=f(Cr,Ω)

(3)

Fay=f(Cr,Ω)

(4)

式中：Fax、Fay表示x、y方向的非線性汽流激振力，N；Cr為偏心距，mm；Ω為渦動頻率，Hz。

1.2 油膜力模型

根據文獻[23]所提出的油膜力模型，在x、y兩個方向上的無量綱油膜力為

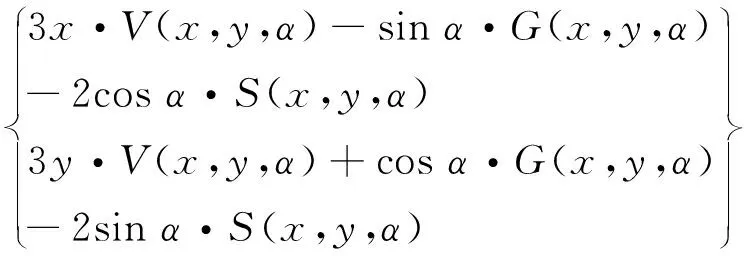
(5)

式中：

(6)

(7)

式中：x、y為軸承無量綱位移;Fx、Fy為非線性無量綱油膜力分量;s為Sommerfeld修正系數；P為轉子質量的一半，kg；μ為潤滑油黏度，Pa·s；b為軸承半徑間隙，mm。

1.3 轉子-軸承-密封系統運動微分方程組

設轉子左端軸承處的徑向位移為x1、y1，圓盤處的徑向位移為x2、y2。建立轉子-軸承-密封系統運動微分方程組如下

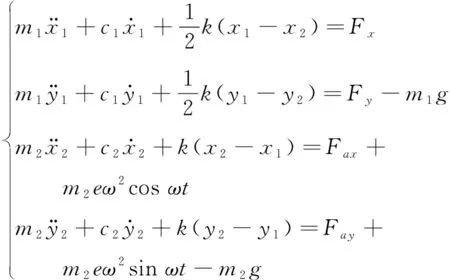
(8)

令

得到系統無量綱化的運動微分方程組如下

(9)

2 計算結果及分析

本文利用MATLAB采用ODE45變步長Runge-Kutta法求解二階微分方程組，總共求解600個周期的數據，舍棄前面500個周期以消除瞬態響應的影響，保留后面100個周期的數據進行分析。對某1 000 MW汽輪機高壓轉子和兩端軸承模化后確定方程的主要參數如表3所示。

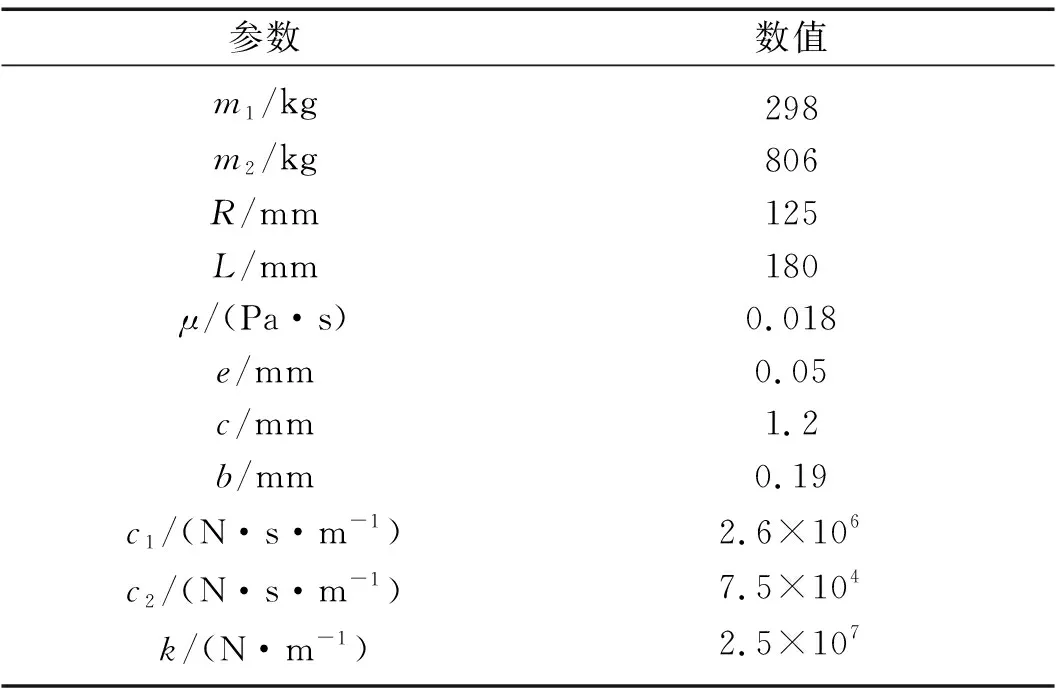
表3 方程的主要參數Tab.3 Main parameters of the equation

2.1 非線性汽流激振力對系統運動特性的影響

圖6(a)和圖6(b)分別為汽輪機轉子-軸承-密封系統沖轉升速過程中的分岔圖和在額定轉速下不同負荷的分岔圖。非線性汽流激振力隨著負荷的增加而增加，由前面的數值計算部分求出。從圖6(a)可以看出，系統在只有質量偏心力、重力和油膜力的作用下，依次經歷了向外發散的極限環運動(圖7(a))、倍周期運動(圖7(b))、二周期運動(圖7(c))、一周期運動(圖7(d))，在額定轉速下是一周期運動。

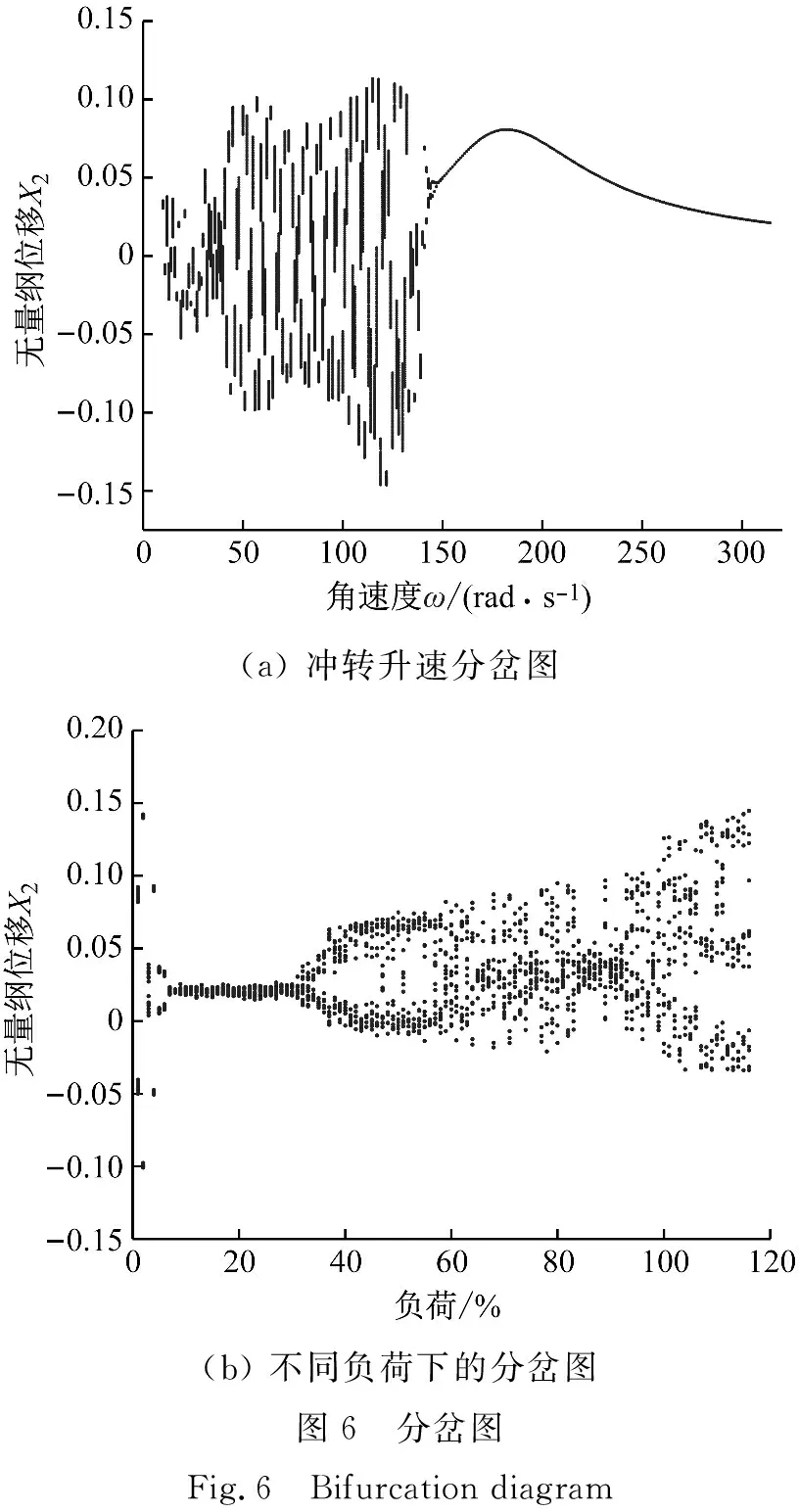
從圖6(b)可以看出，在非線性汽流激振力、質量偏心力，重力和油膜力作用下，在1%THA～6%THA之間，分岔圖是不連續分布的兩處豎著的點線段，這是有混沌傾向的“二周期”運動的特征；在7%THA～35%THA之間，分岔圖是密集的窄點帶，系統進入類似“一周期”的混沌運動；在35%THA～60%THA之間，分岔圖主要是上下兩條點帶，在50%THA附近兩條點帶之間存在散點，這是類似“二周期”的混沌運動；在60%THA～85%THA之間，分岔圖兩條點帶演化為凌亂的散點，在63%THA、72%THA和81%THA附近，分岔圖的散點較集中，在75%THA附近，散點區域寬度接近一致，系統進入復雜的混沌運動；此后散點發散，87%THA附近散點分布很開，隨著負荷升高，散點的分布越來越寬；在110%THA時，開始形成上中下三部分散點域，如果汽輪機超負荷運行，系統將進入類似“三周期運動”的混沌運動。

圖8為非線性汽流激振力作用下幾種典型運動的代表性頻譜圖、軸心軌跡圖和Poincare截面映射圖。4%THA工況中X2、Y2方向的1/2工頻振動相似且對應的工頻振動也相似，且15%THA工況中X2、Y2方向的工頻振動相似。對比不同負荷下X2、Y2方向的頻譜圖可以發現，4%THA的1/2工頻振動分量較大，而15%、114%THA的X2、Y2方向的頻譜圖的1/2工頻分量不明顯，另外35%、60%THA的X2、Y2方向的頻譜圖都有1/2工頻。在超負荷運行下(如114%THA)，X2、Y2方向的頻譜圖的1/2工頻演變為1/3和2/3工頻。隨著負荷增加，Y2方向的工頻幅值比X2方向的工頻大。在高負荷，X2方向的分頻幅值比Y2方向的大。60%THA時，在1/2工頻處出現重頻現象。超負荷運行時(如114%THA)，Y2方向的工頻幅值比X2方向的工頻大3%，且X2方向的1/3工頻幅值是2/3工頻幅值的2倍，而Y2方向的1/3工頻幅值是2/3工頻幅值的2/3倍。此時，非線性汽流激振力對系統運動特性的影響更劇烈。

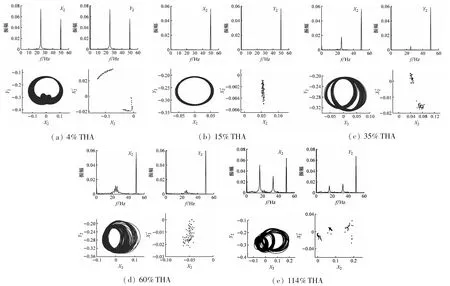
圖8 不同負荷下的頻譜圖，軸心軌跡圖和Poincare截面映射圖Fig.8 Spectrum diagram, axis track diagram and Poincare section map under different load

從軸心軌跡圖和Poincare截面映射圖來看，在4%THA處，軸心軌跡圖在下側形成一個“心”形圖案，軌跡線左側是逐漸向內運動，右側是逐漸向外運動，往復循環，對應的截面圖是兩條點帶，左上角的點帶平直光滑，右下角的點帶呈一個拐角形狀，這是有混沌傾向的二周期運動的特征。在15%THA處，軸心軌跡圖是密集軌跡線重疊交叉形成的環帶，對應的截面圖是一條豎著的點帶，此時的運動為類似“一周期”的混沌運動。在35%THA處，軸心軌跡圖是由密集軌跡線形成的類似“二周期”的運動圖案，在下側軌跡發生交叉，在上側軌跡發生重疊，最右側的環帶相對較稀疏，對應的截面圖是兩個散點區域，這是類似“二周期”的混沌運動。在60%THA處，軸心軌跡圖沒有明顯的密集軌跡線所形成的環帶，軌跡交錯紊亂，軌跡間隔不均勻，出現脫離主體圖形的軌跡，對應的截面圖是一堆傾斜的散點，顯現出混沌運動的特征。在超負荷運行時，軸心軌跡圖是由密集軌跡線形成的類似“三周期”的運動圖案，最右側的環帶發生分離，分離出去一個稀疏的軌跡環帶，對應的截面圖是三處散點域，右側的點域在下部分布著散點，此時的運動類似“三周期”的混沌運動。

此外，從坐標跨度來看，隨著負荷增加，X2、Y2方向的坐標跨度先減小后增大。

綜上所述，在汽輪機沖轉升速過程中，轉子系統的運動軌跡都比較穩定，主要都是軌跡清晰的圓周運動。在高轉速下，系統進入一周期運動，且隨著轉速升高，軌跡的運動幅度越來越小，在額定轉速下，系統穩定運行。隨著負荷增加，非線性汽流激振力對系統的作用開始顯現，軌跡的運動幅度先減小后增大，在額定負荷下系統處于混沌運動。

2.2 非線性汽流激振力對系統穩定性的影響

Lyapunov指數是衡量系統動力學特性的一個重要定量指標[24]。對于系統是否存在動力學混沌，可以從最大Lyapunov指數是否大于零來判斷。一個負最大Lyapunov指數，則意味著在系統相空間中相鄰點最終要靠攏合并成一點，這對應于穩定的不動點和周期運動；一個正最大Lyapunov指數，則意味著無論初始兩條軌線的間距多么小，其差別都會隨著時間的演化而成指數率的增加以致達到無法預測，這就是混沌現象。一旦系統處于混沌狀態，系統將失穩。值得指出的是，在混沌運動中也有與周期運動相似的運動形態，表現為混沌運動的軌跡線呈現周期趨勢，即所謂的“周期”混沌現象。

本文采用Wolf法計算非線性汽流激振力作用下轉子系統的最大Lyapunov指數，如圖9所示。

從圖9可以看出，低負荷時，有混沌傾向的“二周期”運動對應的指數值在零左右徘徊，說明此時的混沌性不強，隨后進入“一周期”混沌運動，指數值急劇上升。此后進入“二周期”混沌運動，指數值降低。“二周期”混沌運動的指數值比“一周期”混沌運動的小，這說明在周期性混沌運動中，“一周期”混沌運動反而蘊含著相比“二周期”混沌運動更復雜的混沌信息。其原因在于一周期混沌運動的位移呈跳躍性變化，而二周期混沌運動位移呈連續變化。此后系統進入復雜紊亂的混沌運動，由于是由“二周期”混沌運動過渡，后面復雜紊亂的混沌運動的指數值與前面的“二周期”混沌運動的指數值有相當的數值。值得注意的是，最后的混沌運動有“三周期”特征，這反應了在非線性汽流激振力作用下系統的混沌運動相當復雜。隨著負荷增加，周期性混沌運動向復雜紊亂的混沌運動演化，當負荷達到某個程度時復雜紊亂的混沌運動又演化為周期性的混沌運動。但是，不管Lyapunov指數值變化多么復雜，在整個負荷變化區間內數值都較小，說明隨著負荷的增加，轉子系統的混沌特性相對不是很強。

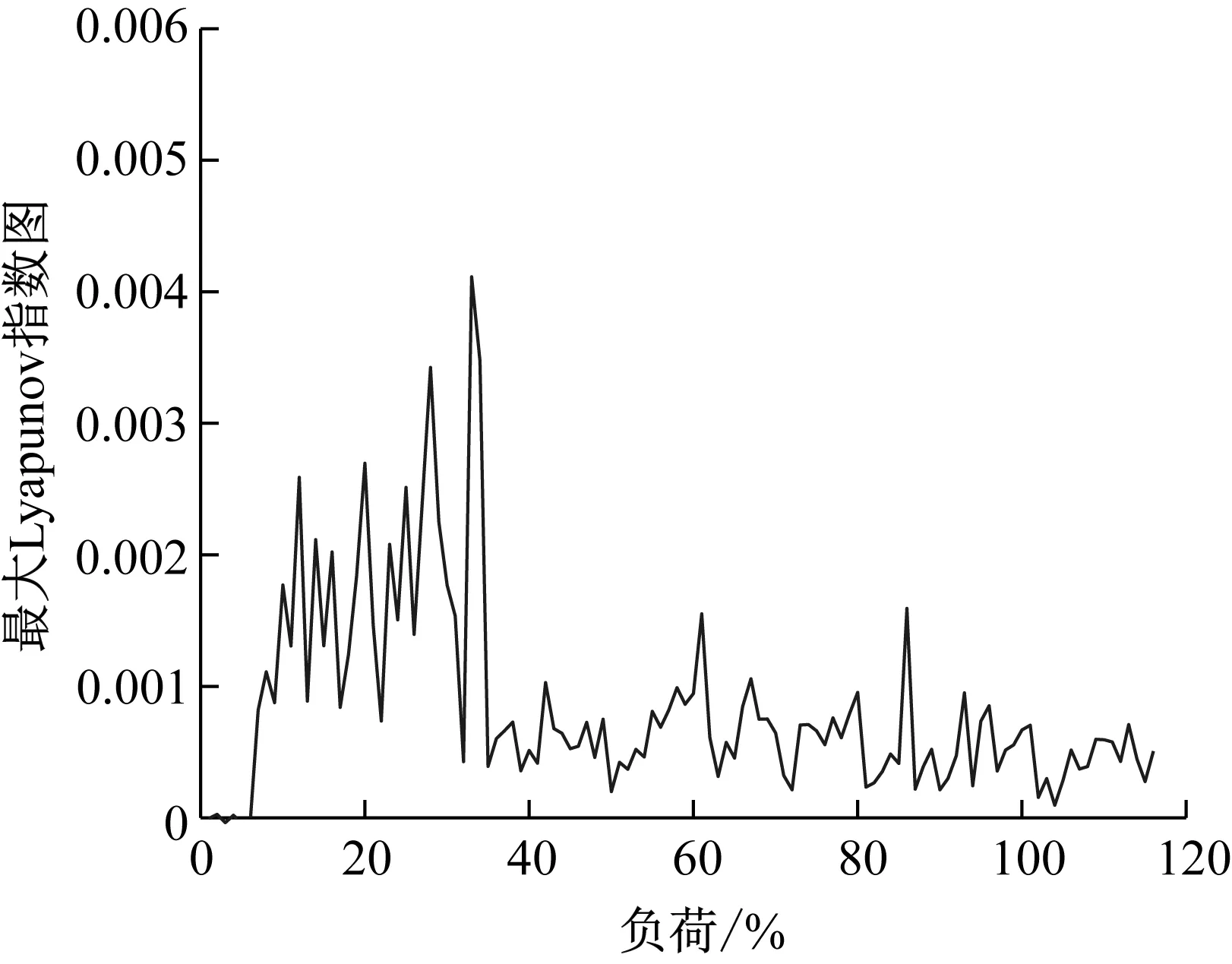
圖9 最大Lyapunov指數圖Fig.9 Maximum Lyapunov exponents

3 結 論

本文建立某1 000 MW超超臨界汽輪機高壓缸1.5級三維全周模型，通過數值模擬得到非線性汽流激振力，并利用Runge-Kutta法求解微分方程組，分析非線性汽流激振力對汽輪機轉子-軸承-密封系統穩定性的影響。具體結論如下：

(1) 在汽輪機沖轉升速過程中，非線性汽流激振力很弱，轉子系統經歷了極限環運動、倍周期運動和二周期運動，并在額定轉速時為一周期運動。隨著負荷增加，非線性汽流激振力增強，轉子系統經歷了有混沌傾向的“二周期”運動、“一周期”混沌運動、“二周期”混沌運動、復雜紊亂的混沌運動和“三周期”混沌運動。在額定負荷下，系統處于較弱的混沌運動。

(2) 非線性汽流激振力以分頻的形式影響轉子運動。低負荷時系統振動以1/2工頻為主；隨著負荷升高，振動以工頻為主；在高負荷下，系統出現了1/3工頻和2/3工頻。

(3) 變負荷的指數圖表明“一周期”混沌運動比“二周期”混沌運動蘊含的混沌信息更豐富和復雜。隨著負荷增加，受非線性汽流激振力的影響，系統處于混沌運動，最大Lyapunov指數大于零，系統可能失穩。