基于脈動法的上海市RC剪力墻結構基本自振周期測試與分析

閆培雷， 郭恩棟， 吳厚禮， 金宇航

(中國地震局工程力學研究所 中國地震局地震工程與工程震動重點實驗室,哈爾濱 150080)

上海市高層建筑從20世紀80年代的121幢已經發展到如今的3萬余幢[1]，由于整體性好、側移剛度大、承載力高等優點[2]，剪力墻結構在30層以下的高層建筑中得到廣泛應用，已成為上海市的主要建筑結構類型之一。作為人口財富密集型的超大城市，上海市面臨著潛在巨大的地震和臺風災害風險。剪力墻結構在地震或臺風作用下響應與破壞取決于結構動力特性和外部荷載特性。結構動力特性是建筑自身固有的特性，包括自振周期、振型和阻尼比等，其中基本自振周期是其中極重要的參數之一，用于估算結構承受的地震作用與風荷載。因此，確定結構基本自振周期對結構的抗震抗風設計、維修加固、安全性評估以及損傷識別具有十分重要的意義。

在我國，結構自振周期一般采用經驗公式計算獲得，經驗公式法是對特定類型建筑進行大量動力性能測試，通過回歸分析擬合給出基本自振周期經驗公式[3-16]。相較于理論計算獲得的基本自振周期，動力性能測試結果是建筑真實性態的反應，排除了各種假定的影響，如質量分布、材料實際性能、節點剛度、填充墻布置以及施工質量等，數據準確可靠。因此，經驗公式法是一種用于快速估算結構動力特性的可靠方法。

在結構初始設計階段，設計者多依據文獻[17]中的經驗公式估算剪力墻結構的基本自振周期。該公式是基于20世紀六七十年代在北京、上海、天津、廣州、成都等十幾個城市內80余棟高度在50 m以下的結構實測數據擬合而成的[18]。四十多年以來，隨著我國鋼筋混凝土結構的相關規范和標準逐步修訂完善，剪力墻結構的抗震措施發生了顯著變化，結構高度大多超過50 m，目前對于高度超過50 m鋼筋混凝土剪力墻結構的動力特性的研究較少[19-20]。針對上述問題，本文通過對上海市已建成的62棟剪力墻結構進行動力性能測試，獲得了結構水平縱橫兩個方向上的基本自振周期；采用其中的60棟結構的數據進行回歸分析，分別給出了以高寬比和總高度為自變量的高度范圍在45～90 m的基本自振周期的經驗公式；并用2棟結構的數據驗證了公式的可靠度。相較于文獻[11]和[12]，在參照文獻[17]給出了基于高寬比的鋼筋混凝土剪力墻結構基本自振周期經驗公式的基礎上，同時參考美國相關規范[21-23]，給出了采用“冪次高度系數”形式的結構基本自振周期經驗公式，該公式較我國現行規范中相關公式的形式更為簡潔且自變量數量更少，本文給出的公式是對相關規范的補充和完善。

1 RC剪力墻結構的脈動測試及結果

1.1 測試結構的基本情況

本文對上海市的62棟RC剪力墻結構采用脈動法進行了結構動力性能測試。脈動法是利用自然環境對結構不規則的微弱干擾，不用任何激振設備，通過結構脈動響應來確定測試結構的動力特性，不會對測試結構造成損傷，也不影響其正常使用。

作為測試樣本的RC剪力墻結構以住宅為主，平面布置基本規則對稱且平面形狀以矩形為主，豎向剛度基本均勻，結構總高度的分布如表1所示。

表1 不同總高度范圍內測試樣本數Tab.1 Number of test samples in different total height ranges

1.2 現場脈動測試流程與原則

脈動法測試采用G01NET-2通用數據采集器和941-B超低頻測振儀(如圖1所示)。G01NET-2是多通道數據同步高速采集儀，應用于結構測試中振動信號的采集、分析及處理。941-B型超低頻測振儀是用于測量結構在環境激勵下的低頻脈動信號。

圖1 脈動測試采用的儀器和設備Fig.1 Instruments and equipment for pulsation testing

為保證脈動測試數據準確可靠，現場測試過程中按照以下原則進行：

(1) 測試前搜集結構竣工圖，確定結構總高度、長度、寬度和平面剛度中心；

(2) 測振儀應布置在結構平面剛度中心處的主要承重構件附近，且應沿水平雙向布置，用于保證測振儀接收到的信號以平移振動信號為主，盡量減少扭轉振動信號；

(3) 在結構頂層及一半高度處的樓層布置測振儀，不必層層布置測振儀；

(4) 單次測試時間至少保證5分鐘以上；

(5) 確保每棟結構均設置2個測試位置，每個測位置分別測試3次，每次測試包含水平縱向和水平橫向2組數據。

1.3 數據處理與結果

以上海市嘉定區曹安公路黃渡3#地塊9號樓為例，將測試數據經過傅里葉變換得到自功率譜(如圖2所示)，進行阻尼識別后，通過結構自功率譜峰值可確定其水平方向上的基本自振頻率，而基本自振周期為基本自振頻率的倒數，可得一組數據下結構的基本自振周期(如圖3所示)，并將6組結果取平均值，給出結構在水平縱橫兩個方向上的基本自振周期。

圖2 水平橫向速度時程數據Fig.2 Velocity time history data in the horizontal direction

圖3 水平橫向自功率譜Fig.3 Power spectrum in the horizontal direction

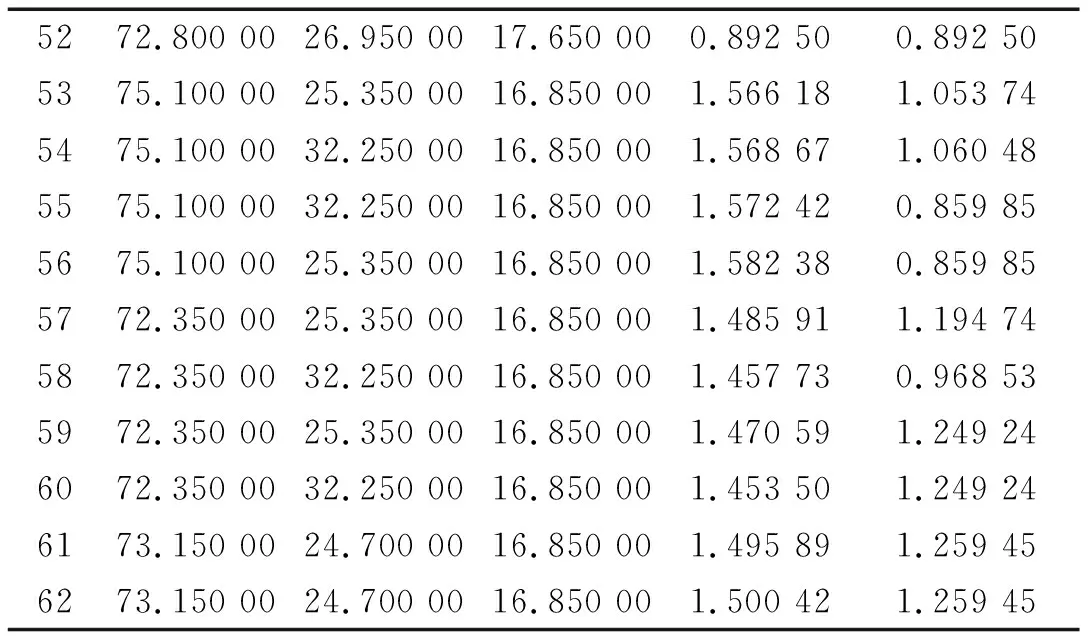
按照上述處理方法，給出上海市62棟結構分別在水平縱橫兩個方向上的基本自振周期(如表2所示)。

表2 實測基本自振周期Tab.2 Measured fundamental natural period

5272.800 0026.950 0017.650 000.892 500.892 50 5375.100 0025.350 0016.850 001.566 181.053 74 5475.100 0032.250 0016.850 001.568 671.060 48 5575.100 0032.250 0016.850 001.572 420.859 85 5675.100 0025.350 0016.850 001.582 380.859 85 5772.350 0025.350 0016.850 001.485 911.194 74 5872.350 0032.250 0016.850 001.457 730.968 53 5972.350 0025.350 0016.850 001.470 591.249 24 6072.350 0032.250 0016.850 001.453 501.249 24 6173.150 0024.700 0016.850 001.495 891.259 45 6273.150 0024.700 0016.850 001.500 421.259 45

2 RC剪力墻結構基本自振周期的回歸分析

脈動實測值反映的是結構微小變形時的動力特性，其往往小于抗震設計中采用反應譜法時的基本自振周期。若按照實測數據統計基本自振周期分布規律，將導致水平地震作用增大。因此，需對實測基本自振周期值進行修正。文獻[24]出自中國建筑科學研究院工程抗震研究所編制的《抗震驗算與構造措施(86年設計規范背景資料、條文解說匯編) 》，其研究表明：針對RC剪力墻結構而言，用于統計回歸基本自振周期的脈動實測值小于抗震分析時的周期值，一般需要進行修正并且取修正值為1.3。該參數被中國建筑科學研究院1984年編制的《工業與民用建筑抗震設計規范(TJ11-78)條文修改報告:筋混凝土框架及剪力墻房屋自振周期經驗公式的建議》所收錄，并于1987年被《建筑結構荷載(GBJ 9—1987)》正式采納，一直沿用至《建筑結構荷載(GBJ 50009—2012)》。因此，取修正參數為1.3具有較好的可靠性。

2.1 結構水平橫向

文獻[17]中RC剪力墻結構基本自振周期經驗公式如下所示

(1)

采用該公式的形式，以結構的總高度和寬度為自變量，以結構水平橫向上的基本自振周期為自變量，基于SPSS22.0統計分析軟件對60棟結構的水平橫向基本自振周期進行回歸分析，分析結果如圖4所示。

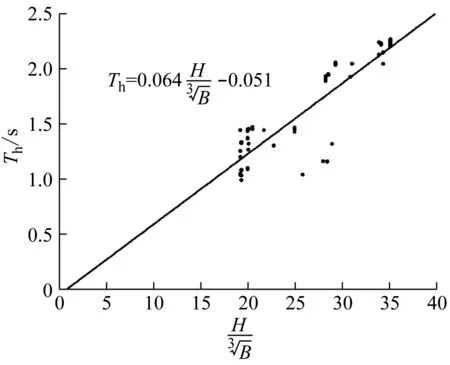
圖4 基于結構總高度和寬度的橫向基本自振周期經驗公式Fig.4 Empirical formula of the horizontal fundamental natural period based on total height and width of structures

則結構水平橫向上的基本自振周期經驗公式為

(2)

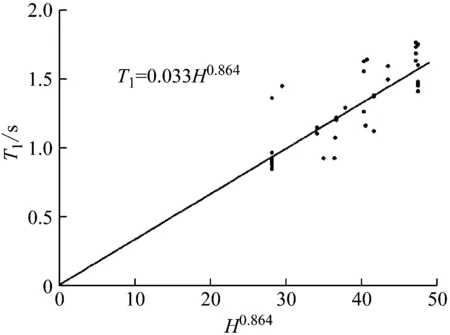
式中，45 m

美國相關規范中鋼筋混凝土剪力墻結構的基本自振周期經驗公式多采用“冪次高度系數”的形式，其系數是根據大量強震記錄所得的數據擬合而成。因此，采用“冪次高度系數”的形式，以結構總高度為自變量，以水平橫向上的基本自振周期為自變量，基于SPSS22.0統計分析軟件對60棟結構的水平橫向基本自振周期進行回歸分析，分析結果如圖5所示。

圖5 基于結構總高度的橫向基本自振周期經驗公式Fig.5 Empirical formula of the horizontal fundamental natural period based on total height of structures

則結構水平橫向上的基本自振周期經驗公式為

Th=0.03H0.944

(3)

式中，45 m

決定系數，又稱擬合優度，在統計學中用于度量因變量的變異中可由自變量解釋部分所占的比例，以此來判斷統計模型的解釋程度。對比式(2)和式(3)發現，式(3)的決定系數高于式(2)的決定系數，說明在水平橫向上，結構總高度對結構基本自振周期的影響比結構總高度和寬度的影響大。

2.2 結構水平縱向

采用文獻[17]中的公式形式，以結構的總高度和長度為自變量，以結構水平縱向上的基本自振周期為自變量，基于SPSS22.0統計分析軟件對60棟結構的水平縱向基本自振周期進行回歸分析，分析結果如圖6所示。

圖6 基于結構總高度和長度的橫向基本自振周期經驗公式Fig.6 Empirical formula of the longitudinal fundamental natural period based on total height and length of structures

則結構水平縱向上的基本自振周期經驗公式為

(4)

式中，45 m

采用“冪次高度系數”的形式，以結構總高度為自變量，以水平縱向上的基本自振周期為自變量，基于SPSS22.0統計分析軟件對60棟結構的水平縱向基本自振周期進行回歸分析，分析結果如圖7所示。

圖7 基于結構總高度的橫向基本自振周期經驗公式Fig.7 Empirical formula of the longitudinal fundamental natural period based on total height of structures

則結構水平橫向上的基本自振周期經驗公式為

Tl=0.033H0.864

(5)

式中，45 m

對比式(4)和式(5)發現，式(5)的決定系數略高于式(4)的決定系數，說明在水平縱向上，結構總高度和長度對結構基本自振周期的影響與僅有結構總高度的影響基本相當。

上述分析表明：在上海市的總高度在45～90 m之間的RC剪力墻結構，采用 “冪次高度系數”形式的基本自振周期經驗公式的擬合優度好于采用文獻[17]的形式的經驗公式的擬合優度，且采用 “冪次高度系數”形式的基本自振周期經驗公式的參數少形式簡單。

3 結構基本自振周期經驗公式準確性驗證

選擇兩棟未參與回歸分析的RC剪力墻結構的脈動測試數據，驗證本文給出的結構在水平縱橫兩個方向上的基本自振周期經驗公式(2)～(5)的準確性。

算例1為上海市長風11地塊西北住宅項目6號樓，該結構用途為住宅，高度為64.8 m，長度為34.8 m，寬度為17.5 m，結構如圖8所示。

算例2為上海金橋地鐵保障房8號樓，該結構的用途為住宅，高度為87.4 m，長度為26.6 m，寬度為15.45 m，結構如圖9所示。

從表3中可以看出：

表3 RC剪力墻結構基本自振周期值計算值與經驗值對比Tab.3 Comparison of calculated value and empirical value of fundamental natural period of RC shear wall structure

式(1)給出的結構在水平縱橫兩個方向上的基本自振周期計算值均小于實測周期值，且計算誤差率較大，導致結構初始設計階段估算的水平地震作用偏大。

在結構水平橫向上，式(2)式(3)給出的計算值均大于實測周期值，且式(3)的誤差率小于式(2)的誤差率；在結構水平縱向上，式(4)和式(5)給出的計算值均大于實測周期值，且式(5)的誤差率小于式(4)的誤差率；式(3)和式(5)的計算值更接近于有限元計算結果。上述分析表明，采用 “冪次高度系數”形式的經驗公式的誤差率較低。

4 結 論

基于上海市的 62棟高度在45～90 m的RC剪力墻結構動力性能測試數據，識別了結構在水平縱橫兩個方向上的基本自振周期并進行了回歸分析。本文的主要結論如下：

(1) 對于高度在45～90 m之間的RC剪力墻結構，結構總高度是影響結構基本自振周期的重要因素；

(2) 針對高度在45～90 m之間的RC剪力墻結構，分別給出了基于結構高寬比和“冪次高度系數”的水平縱橫兩個方向上基本自振周期回歸公式，通過兩個實際工程驗證了后者的擬合優度和誤差率均優于前者，本文的研究是對現行規范中結構基本自振周期經驗公式相關規定的補充；

(3) RC剪力墻結構住宅的初始設計階段，在已知結構信息較少的情況下可采用本文給出的式(3)和式(5)估算結構基本自振周期，用于初步估算結構承受的地震作用和風荷載。