巖移沉降觀測(cè)中數(shù)據(jù)缺失的一種估算方法

賴禮泉

(福建省閩東南地質(zhì)大隊(duì)，福建 泉州 362000)

礦區(qū)地表變形監(jiān)測(cè)在施工過(guò)程中至關(guān)重要，通常為持續(xù)性地對(duì)地表進(jìn)行觀測(cè)，并通過(guò)建立數(shù)學(xué)預(yù)測(cè)模型對(duì)地表形變趨勢(shì)預(yù)測(cè)，從而科學(xué)施工，避免事故[1-5]。但在實(shí)際變形監(jiān)測(cè)過(guò)程中，通常會(huì)出現(xiàn)觀測(cè)數(shù)據(jù)缺失的問(wèn)題，主要是由于觀測(cè)點(diǎn)處于裂縫或塌陷區(qū)、被積水淹沒、遭到人為破壞[6]。當(dāng)變形監(jiān)測(cè)數(shù)據(jù)出現(xiàn)缺失時(shí)通常利用填補(bǔ)法進(jìn)行彌補(bǔ)，即利用某種原則構(gòu)造填補(bǔ)值代替缺失數(shù)據(jù)，補(bǔ)全數(shù)據(jù)序列[7]。常用的數(shù)據(jù)填補(bǔ)方法為回歸分析法，計(jì)算過(guò)程簡(jiǎn)單，但由于選用的影響因子具有不可測(cè)性，導(dǎo)致回歸分析法受到限制。本文引入最大期望算法(Expectation Maximization Model,EM)，通過(guò)觀測(cè)數(shù)據(jù)的邊際分布對(duì)缺失數(shù)據(jù)進(jìn)行幾大似然估計(jì)，當(dāng)E步和M步的迭代之間參數(shù)變化小于給定閾值時(shí)得到缺失數(shù)據(jù)填補(bǔ)值。

1 模型的建立

1.1 回歸分析模型的建立

假設(shè)有一組已知的觀測(cè)數(shù)據(jù)x1,x2,…,xk，已知觀測(cè)數(shù)據(jù)不同的觀測(cè)期數(shù)記為xk1,xk2,…,xki，由此構(gòu)建的回歸模型為：

yi=β0+β1x1i+β2x2i+…+βkxki+εi

(1)

式中，yi為y第i次的觀測(cè)值；β0，β1，…，βk為未知回歸參數(shù)；εi為隨機(jī)誤差，εi～N(0,σ2)，且協(xié)方差σεi·εi-τ=0(τ≠0)。

所以誤差方程為：

vi=β0+β1x1i+β2x2i+…+βkxki-yi

(2)

化為矩陣形式為：

V=Aβ-Y

(3)

式中，V=(v1,v2,…,vn)T；β=(β0,β1,…,βn)T；Y=(y1,y2,…,yn)T；

從而得到參數(shù)的最小二乘解為：

(4)

解得回歸方程為：

(5)

進(jìn)行巖移觀測(cè)，當(dāng)出現(xiàn)數(shù)據(jù)缺失時(shí)，通過(guò)上述過(guò)程利用缺失數(shù)據(jù)附近的點(diǎn)建立回歸模型，最終可以得到缺失數(shù)據(jù)的近似值。

1.2 最大期望算法的建立

最大期望算法是由Dempster提出的，是利用不完全數(shù)據(jù)求取幾大似然估計(jì)的算法[8-13]。假設(shè)x(i)為不完全觀測(cè)數(shù)據(jù)，z(i)為數(shù)據(jù)的缺失部分，x(i)與z(i)共同構(gòu)成完整的數(shù)據(jù)序列，設(shè)未知參數(shù)θ=[u,σ]T，其中，u表示z(i)的均值，σ表示z(i)的方差，兩者均未知。

EM算法流程如下：

隨機(jī)初始化未知參數(shù)θ；循環(huán)重復(fù)E步和M步直到收斂。

E(Expectation)步：計(jì)算期望，利用對(duì)隱藏變量的現(xiàn)有估計(jì)值，計(jì)算其最大似然估計(jì)值；對(duì)于每一個(gè)i，根據(jù)上一次迭代的模型參數(shù)來(lái)計(jì)算出z(i)的后驗(yàn)概率，作為z(i)的現(xiàn)估計(jì)值，公式如下：

Qi(z(i))=p(z(i)|x(i);θ)

(6)

M(Maximization)步：最大化，最大化在E步上求得的最大似然值來(lái)計(jì)算參數(shù)的值，M步上找到的參數(shù)估計(jì)值被用于下一個(gè)E步計(jì)算中，這個(gè)過(guò)程不斷交替進(jìn)行。求使Q函數(shù)獲得極大時(shí)的未知參數(shù)θ取值，將似然函數(shù)最大化以獲得新的未知參數(shù)θ，公式如下：

(7)

Qi(z(i))求出來(lái)代入到θ，θ求出來(lái)又反代回Qi(z(i))，如此不斷的迭代，就可以得到使似然函數(shù)最大化的參數(shù)θ了。

其實(shí)，E步就是求給定X下的條件期望，即后驗(yàn)期望，對(duì)Jensen不等式中小的那一端進(jìn)行放大，使其等于大的那一端，這是一次放大；M步最大化聯(lián)合分布，通過(guò)0梯度，拉格朗日法等方法求極值點(diǎn)，又是一次放大。似然函數(shù)是有界的，只要M步中的0梯度點(diǎn)是極大值點(diǎn)，一直放大下去就能找到最終所求。

具體計(jì)算過(guò)程如下：

如果θ(i)就是第i+1次迭代開始時(shí)的參數(shù)估計(jì)值，則第i+1次迭代時(shí)的E步與M步如下：

E步：Qi(z(i))=p(z(i)|x(i);θ(i))

(8)

M步：θ(i+1)=argmax∑i∑z(i)Qi(z(i))

(9)

通過(guò)上述步驟完成了一次迭代過(guò)程θ(i)→θ(i+1)，繼續(xù)進(jìn)行迭代，過(guò)程如下：

E步：Qi(z(i))=p(z(i)|x(i);θ(i+1))

(10)

M步：θ(i+2)=argmax∑i∑z(i)Qi(z(i))

(11)

通過(guò)上述步驟完成了一次迭代過(guò)程θ(i+1)→θ(i+2)，繼續(xù)進(jìn)行迭代，過(guò)程如下：

E步：Qi(z(i))=p(z(i)|x(i);θ(i+2))

(12)

M步：θ(i+3)=argmax∑i∑z(i)Qi(z(i))

(13)

通過(guò)上述步驟完成了一次迭代過(guò)程θ(i+2)→θ(i+3)，將E步和M步不斷進(jìn)行迭代，直到‖θ(i+1)-θ(i)‖充分小，說(shuō)明殘差已經(jīng)滿足要求，即停止迭代。

2 算例分析

選取某礦區(qū)730采區(qū)測(cè)量原始數(shù)據(jù)，730采區(qū)位于礦井東南部，-980 m延深水平的南部，南至鐵路保護(hù)煤柱(礦井南部邊界)，東南至礦井東南部邊界，東至南部軌道集中巷及其東南方向延長(zhǎng)線，北至-980 m水平一節(jié)軌道及二節(jié)膠帶暗斜井，西至支斷層。采區(qū)南北長(zhǎng)1 469～2 009 m，東西寬318～1 518 m，面積約為2.47 km2。測(cè)線布置重點(diǎn)區(qū)域采用點(diǎn)間距25 m，根據(jù)現(xiàn)場(chǎng)條件做一定調(diào)整，測(cè)線布置圖如圖1所示，其中，加粗線為陀螺邊。

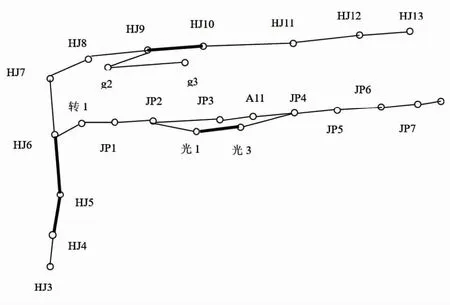
圖1 測(cè)線布置圖

為了比較回歸分析法和EM法對(duì)缺失的下沉數(shù)據(jù)預(yù)測(cè)效果，在完備數(shù)據(jù)中先剔除部分觀測(cè)值，選取A11點(diǎn)2015年12月10日～2016年11月24日共10期觀測(cè)數(shù)據(jù)進(jìn)行試驗(yàn)，圖2為A11點(diǎn)利用回歸分析法和EM法對(duì)10期數(shù)據(jù)的估算結(jié)果與原始觀測(cè)數(shù)據(jù)對(duì)比結(jié)果，其中，縱軸為沉降值，單位為m。

圖2 A11點(diǎn)利用回歸分析法和EM法的估算結(jié)果與原始觀測(cè)數(shù)據(jù)對(duì)比結(jié)果

由圖2可知，回歸分析法和EM法對(duì)缺失數(shù)據(jù)的估算結(jié)果都在原始觀測(cè)數(shù)據(jù)附近，說(shuō)明這兩種方法都可以對(duì)缺失沉降觀測(cè)數(shù)據(jù)進(jìn)行估算；EM法缺失數(shù)據(jù)估算結(jié)果走勢(shì)與觀測(cè)數(shù)據(jù)更加接近，表明EM法對(duì)缺失數(shù)據(jù)估算結(jié)果優(yōu)于回歸分析法。為了更加直觀的對(duì)比兩種估算方法的精度，把殘差的絕對(duì)值和殘差平方和作為對(duì)比指標(biāo)。殘差為實(shí)際觀測(cè)數(shù)據(jù)與估算填補(bǔ)數(shù)據(jù)的差值。實(shí)際觀測(cè)數(shù)據(jù)與兩種方法估算填補(bǔ)數(shù)據(jù)殘差絕對(duì)值對(duì)比結(jié)果如表1所示。

表1 實(shí)際觀測(cè)數(shù)據(jù)與兩種方法估算填補(bǔ)數(shù)據(jù)殘差絕對(duì)值對(duì)比結(jié)果/m

由表1可知，回歸分析法估算填補(bǔ)數(shù)據(jù)殘差絕對(duì)值在0.643～0.986 m之間，其中，最大為第12期數(shù)據(jù)的0.986 m，最小為第14期數(shù)據(jù)的0.643 m。EM法估算填補(bǔ)數(shù)據(jù)殘差絕對(duì)值在0.103～0.360 m之間，其中，最大值為第14期數(shù)據(jù)的0.360 m，最小為第20期數(shù)據(jù)的0.103 m。從估算填補(bǔ)數(shù)據(jù)的殘差絕對(duì)值來(lái)看EM法效果更好。

表2 兩種方法估算填補(bǔ)數(shù)據(jù)中誤差對(duì)比結(jié)果/m

由表2可知，回歸分析法填補(bǔ)數(shù)據(jù)中誤差為0.851 m，EM法填補(bǔ)數(shù)據(jù)中誤差為0.219 m，EM法的中誤差僅為回歸分析法的25.73%，說(shuō)明算法中EM法的迭代計(jì)算能夠有效獲取原始數(shù)據(jù)的規(guī)律，更為準(zhǔn)確地補(bǔ)充缺失的數(shù)據(jù)；實(shí)際計(jì)算時(shí)應(yīng)根據(jù)需求的精度，調(diào)整閾值‖θ(i+1)-θ(i)‖，在達(dá)到精度時(shí)停止式(13)的計(jì)算。

3 結(jié) 論

針對(duì)巖移沉降觀測(cè)中數(shù)據(jù)缺失的問(wèn)題，本文介紹了回歸分析法和EM法對(duì)缺失數(shù)據(jù)估算填補(bǔ)，利用某礦區(qū)巖移沉降觀測(cè)數(shù)據(jù)進(jìn)行實(shí)驗(yàn)，對(duì)實(shí)驗(yàn)結(jié)果對(duì)比分析發(fā)現(xiàn)：

(1)EM法估算數(shù)據(jù)走勢(shì)更接近實(shí)際觀測(cè)數(shù)據(jù)，回歸分析法雖然誤差較大，但與實(shí)測(cè)數(shù)據(jù)偏離不大；

(2)雖然EM法精度較高，但計(jì)算復(fù)雜，需要重復(fù)迭代，時(shí)間較長(zhǎng)，若實(shí)際工程中對(duì)巖移缺失補(bǔ)充精度要求不高，也可以使用回歸分析法計(jì)算其概略值；

(3)回歸分析法填補(bǔ)數(shù)據(jù)中誤差為0.851 m，EM法填補(bǔ)數(shù)據(jù)中誤差為0.219 m，可知EM多次迭代后精度相對(duì)回歸分析法有較大幅度提升，實(shí)際工程中若對(duì)缺失數(shù)據(jù)精度要求高，可以考慮增加迭代次數(shù)，犧牲時(shí)間以獲得更好的巖移沉降觀測(cè)缺失數(shù)據(jù)補(bǔ)充；

(4)需要注意的是，隨機(jī)初始化未知參數(shù)θ的選取對(duì)最終迭代結(jié)果的準(zhǔn)確性有著決定性的影響，若θ選取錯(cuò)誤，最終迭代結(jié)果可能會(huì)出現(xiàn)不收斂或精度偏低的情況，如何準(zhǔn)確地選取有利于迭代計(jì)算的θ值是下一步的重點(diǎn)研究?jī)?nèi)容。